Study of the area of attraction of the auto-balancing mode in a ball-type automatic balancing device with a horizontal axis of rotation

Strautmanis, Guntis; Mezitis, Mareks; Strautmane, Valentina; Gorbenko, Alexander; Shchukins, Igors; Gromova, Marina

doi:10.21595/vp.2019.20656

Vibroengineering Procedia

Browse Procedia

Published: 07 June 2019

Check for updates

Study of the area of attraction of the auto-balancing mode in a ball-type automatic balancing device with a horizontal axis of rotation

Guntis Strautmanis¹

Mareks Mezitis²

Valentina Strautmane³

Alexander Gorbenko⁴

Igors Shchukins⁵

Marina Gromova⁶

^{1, 2, 6}Riga Technical University, Riga, Latvia

^{3, 5}Riga Technical University, Daugavpils, Latvia

⁴Kerch State Maritime Technological University, Kerch, Russia

Corresponding Author:

Guntis Strautmanis

Cite the article Download PDF

Abstract

It is known that automatic balancing devices are capable of reducing vibrations in rotary systems in a superresonance velocity zone. However, the effectiveness of automatic balancing devices is related to the necessity of accelerating compensating masses. To ensure the acceleration of compensating masses from standstill to the operating speed of the rotor, they need to be provided some initial velocity. The value of this velocity is influenced by the parameters of the elastic suspension of the rotor, the geometrical parameters of the automatic balancer, the coefficient of rolling friction between the housing and the compensating mass, etc. The work is devoted to the study of a horizontal rotor model with an automatic balancer with one compensating mass, in particular the issue on the influence of the coefficient of viscous friction on the value of the area of attraction of the auto-balancing mode.

Study of the area of attraction of the auto-balancing mode in a ball-type automatic balancing device with a horizontal axis of rotation

Highlights

In the rotor system with ABD various stable modes of motion are possible (nearly periodic, superharmonic, and other oscillations)
The increase in the viscous friction coefficient in ABD narrows the range of existence of nearly periodic and superharmonic modes of motion of the rotor system
Reducing the coefficient of viscous friction in the ABD slightly reduces the area of attraction of the main auto-balancing mode

1. Introduction

Reducing the vibration of an unbalanced rotor in the superresonance frequency band can be accomplished by installing an automatic balancing device (ABD) on the rotor, while the amount of imbalance can be variable, such as in grinding machines, centrifuges, etc. When installing a ball-type ABD on a horizontal rotor, the problem arises of acceleration of compensating masses (CM) and stability of the auto-balancing mode due to the influence of gravity on the motion of CM. As noted in [1], the effect of gravity causes additional resonance during acceleration of the rotor with an ABD. In addition, the action of gravity leads to the multimode of the ABD in the transient acceleration mode of CM to the operating speed of the rotor. The influence of the rotor suspension parameters on the acceleration of the CM in a ring of a rectangular cross section of an ABD and the influence of resistance forces on the accuracy of automatic balancing are considered in [2, 3]. Therefore, it is of interest to consider the influence of the value of internal friction in an ABD on the area of attraction of the auto-balancing mode.

It is of interest to construct the amplitude-frequency characteristic and the area of attraction of the auto-balancing mode of the rotor system at various values of internal friction in an ABD for the analysis of a range of application of an ABD with a horizontal axis of rotation. In the case when an ABD loses auto-balancing mode and goes into another mode, the rotor has increased vibrations [4, 5]. The results of the work can be used in the design and calculation of parameters of a ball-type ABD for rotary systems with a horizontal axis of rotation.

The aim of the work is to study the area of attraction of the auto-balancing mode of a horizontal rotor with a ball-type ABD with one CM. The work is a continuation of works [6, 7] related to the study of acceleration of CM in an automatic balancing device and is based on experimental tests of the rotor with an ABD [8].

2. Design model and mathematical model of a rotor with an ABD

The paper deals with a symmetric horizontal rigid rotor on an elastic-dissipative suspension and with an ABD. The ABD housing is made in the shape of a ring with radius $R$ on the average circumference, into which one compensating mass in the shape of a ball of radius $r$ and mass $m$ is placed. A viscous friction force with a viscous friction coefficient $b_{0}$ acts on the compensating mass. The rotor of mass $m_{r}$ has a static eccentricity $e$ , and it is mounted to the suspension with stiffness and viscous friction coefficients c and b, respectively. The ABD housing is concentrically mounted on the rotor and rotates along with it with angular velocity $ω =$ const.

The design model of the rotor with an ABD, shown in Fig. 1. The compensating mass begins its movement from the position and velocity, which are set by the initial conditions.

Fig. 1Design model of a rotor system with an ABD

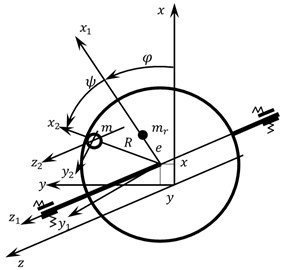
a)

b)

The rotor system has three degrees of freedom, so the mathematical model consists of three differential equations of motion, given in a dimensionless form with respect to $r p^{2}$ :

1

\ddot{\bar{x}} = - b_{r} \dot{\bar{x}} - \bar{x} + m_{0} \frac{1}{r_{0}} {(ω_{0} + \dot{\bar{ψ}})}^{2} c o s (φ + \bar{ψ}) + m_{0} \frac{1}{r_{0}} \ddot{\bar{ψ}} s i n (φ + \bar{ψ})

+ (1 - m_{0}) e_{0} ω_{0}^{2} c o s (φ) - (1 - m_{0}) g_{0},

2

\ddot{\bar{y}} = - b_{r} \dot{\bar{y}} - \bar{y} + m_{0} \frac{1}{r_{0}} {(ω_{0} + \dot{\bar{ψ}})}^{2} s i n (φ + \bar{ψ}) - m_{0} \frac{1}{r_{0}} \ddot{\bar{ψ}} c o s (φ + \bar{ψ})

+ (1 - m_{0}) e_{0} ω_{0}^{2} s i n (φ),

3

\frac{7}{5} \ddot{\bar{ψ}} = \ddot{\bar{x}} r_{0} s i n (φ + \bar{ψ}) - \ddot{\bar{y}} r_{0} c o s (φ + \bar{ψ}) - b_{b} \dot{\bar{ψ}} + g_{0} r_{0} s i n (φ + \bar{ψ}) .

The calculations were made at the following values of dimensionless parameters of the rotor system:

b_{r} = \frac{β_{r}}{p} = 0,2, b_{b} = \frac{β_{b}}{p} = (2,875 \dots 11,50) ∙ 10^{- 3}, r_{0} = \frac{r}{R} = 0,0575,

e_{0} = \frac{e}{r} = 0,08696, g_{0} = \frac{9,81}{r p^{2}} = 8,53, m_{0} = \frac{m}{M} = 0,005,

where:

β_{r} = \frac{b}{M}, β_{b} = \frac{b_{0}}{m}, p^{2} = \frac{c}{M}, φ = 2 π τ + φ_{0} .

The results of the calculations are obtained in the form of dimensionless accelerations, velocities and coordinates of the rotor system, having the following form:

\ddot{\bar{x}} = \frac{\ddot{x}}{r p^{2}}, \ddot{\bar{y}} = \frac{\ddot{y}}{r p^{2}}, \ddot{\bar{ψ}} = \frac{\ddot{ψ}}{p^{2}}, \dot{\bar{x}} = \frac{\dot{x}}{r p}, \dot{\bar{y}} = \frac{\dot{y}}{r p}, \dot{\bar{ψ}} = \frac{\dot{ψ}}{p}, \bar{x} = \frac{x}{r}, \bar{y} = \frac{y}{r}, \bar{ψ} = ψ .

3. Results of the research of the mathematical model

The system of differential equations of motion Eqs. (1-3) of a rotor system with the ABD with one CM was investigated using the SPRING program [9].

In the work, the impact of the viscous friction coefficient inside the ABD on the value of the area of attraction of the auto-balancing mode is considered. The initial position of $ψ$ and the initial velocity of the CM in the circular direction of the balancer $\dot{\bar{ψ}} = \dot{ψ} / p$ was determined when the CM returns to the auto-balancing mode. When building the area of attraction of auto-balancing mode, the parameters of the fixed point, corresponding to a stable rotary system motion mode, were determined from the amplitude-frequency characteristic (AFC). The parameters of the fixed point are given in Table 1.

Researches were conducted at various fixed values of the dimensionless viscous friction coefficient in the automatic balancing device $b_{b} =$ 2,875×10^-3 and $b_{b} =$ 11,50×10^-3. The mass of the CM was accepted depending on its radius and was determined by the formula: $m =$ 7,812×10^-3∙4 $π r$ ³/3 kg.

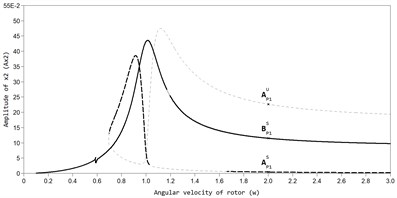
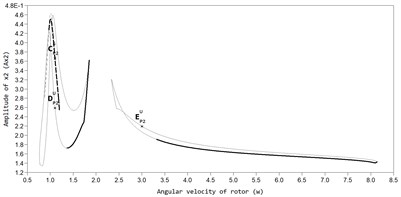
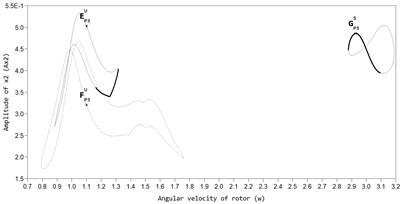
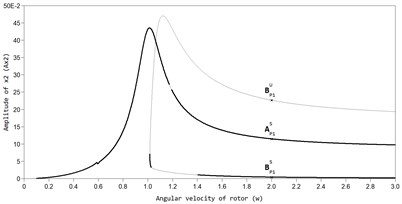
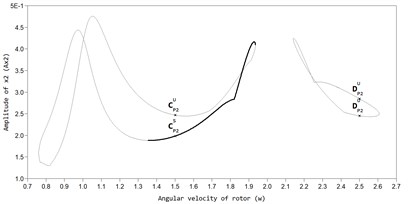
In Fig. 2 and Fig. 3, the AFC graphs of the rotor system are constructed for two values of viscous friction in the ABD (black color marks the branch of periodic stable solutions, grey color branches of unstable solutions). The graphs show that, along with the main periodic auto-balancing mode (mode $A_{P 1}^{S}$ ) there are also modes of superharmonic vibrations P2 and P3 in the system, and non-periodic modes in which the CM is moving relative to the housing of the ABD, while the rotor has increased amplitudes of vibrations.

Fig. 2AFC of a rotor with an ABD in the direction of the axis y at bb= 2,875×10-3: a) AP1S – stable auto-balancing mode; BP1S – stable mode in the absence of automatic balancing, AP1U – unstable mode, b) mode of superharmonic vibrations Р2, c) mode of superharmonic vibrations Р3

AFC of a rotor with an ABD in the direction of the axis y at bb= 2,875×10-3: a) AP1S – stable auto-balancing mode; BP1S – stable mode in the absence of automatic balancing, AP1U – unstable mode, b) mode of superharmonic vibrations Р2, c) mode of superharmonic vibrations Р3

a)

b)

c)

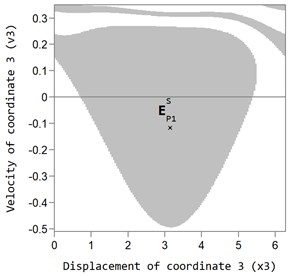
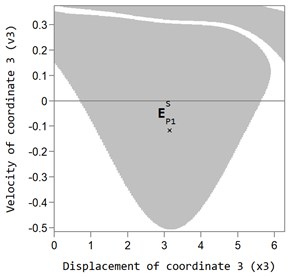
Fig. 4 shows the areas of attraction of the main P1 auto-balancing mode with the value of the dimensionless rotor speed $ω =$ 3 for two fixed values of the viscous friction coefficient inside the ABD ( $b_{b} =$ 2,875×10^-3 and $b_{b} =$ 11,5×10^-3). The grey color indicates the area of the initial values of speed, and coordinates for CM, at which the system returns to the motionless point, which corresponds to the auto-balancing mode.

Fig. 3AFC of a rotor with an ABD in the direction of the axis y at bb= 11,5×10-3: a) BP1S – stable auto balancing mode, AP1S – stable mode in the absence of automatic balancing, BP1U – unstable mode, b) mode of superharmonic vibrations Р2, c) mode of superharmonic vibrations Р3

AFC of a rotor with an ABD in the direction of the axis y at bb= 11,5×10-3: a) BP1S – stable auto balancing mode, AP1S – stable mode in the absence of automatic balancing, BP1U – unstable mode, b) mode of superharmonic vibrations Р2, c) mode of superharmonic vibrations Р3

a)

b)

c)

Fig. 4Area of attraction of the main P1 (grey area) auto-balancing mode at dimensionless rotor velocity ω= 3 and viscous friction coefficient: a) bb= 2,875×10-3, b) bb= 11,5×10-3 (the white area is the area of attraction of superharmonic and non-periodic oscillations of the rotor system)

Area of attraction of the main P1 (grey area) auto-balancing mode at dimensionless rotor velocity ω= 3 and viscous friction coefficient: a) bb= 2,875×10-3, b) bb= 11,5×10-3 (the white area is the area of attraction of superharmonic and non-periodic oscillations of the rotor system)

a)

b)

If we assign the initial values of the speed and coordinates for the CM outside the area of attraction (white area), the rotor system will not return to the auto-balancing mode. In this case, either the nearly periodic or superharmonic oscillation mode of the CM is realized (white area in the graph). Thus, the CM moves with a delay with respect to the housing or rolls down the housing of the ABD, while the rotor performs oscillations exceeding the oscillations in the auto-balancing mode.

An increase in the viscous friction coefficient inside the ABD somewhat expands the area of attraction of the main auto-balancing mode (see Fig. 4(a)) and (b)), however this expansion does not cause a significant effect on the operation of the ABD in the auto-balancing mode.

Table 1Parameters of the fixed point of the auto-balancing mode

Marking	Viscosity coefficient, $b_{b}$	$\bar{x}$	$\dot{\bar{x}}$	$\bar{y}$	$\dot{\bar{y}}$	$\bar{ψ}$	$\dot{\bar{ψ}}$
$A_{P 1}^{S}$	2,875×10^-3	−8,486083	−4,18×10^-4	8,226738×10^-5	8,958×10^-3	3,141004	−0,116446
$B_{P 1}^{S}$	11,50×10^-3	−8,486086	−5,47×10^-4	1,23×10^-4	8,949×10^-3	3,14054	−0,116446

4. Conclusions

The calculations of the mathematical model of a horizontal rotor with a ring-shaped ABD housing concentrically fixed on it with one compensating mass allowed concluding that the amplitude-frequency characteristic essentially depends on the value of the viscous friction coefficient inside the ABD. Depending on the initial conditions of motion of the rotor system at the changes of the angular velocity of the rotor, various stable motion modes can be realized within it. These include nearly periodic, superharmonic modes of motion with a period of P2 and P3. At the same time, an increase in the viscous friction coefficient in ABD narrows the range of existence of nearly periodic and superharmonic modes of motion of the rotor system.

Reducing the coefficient of viscous friction in the ABD slightly reduces the area of attraction of the main auto-balancing mode and expands the area of existence of superharmonic and nearly periodic regimes motion modes of the CM. This circumstance can make it difficult for the ABD to enter the required operating mode. At the same time, it is of interest to further develop the mathematical model of a horizontal rotor with an ABD with two or more CM taking into account the collisions between them.

References

Gorbenko A. N. Influence of gravity on rotor oscillations with a ball self-balancing. Bulletin of the Technological University of Podolia, Vol. 1, 2000, p. 110-114, (in Russian).

Search CrossRef
Sperling L., Ryzhik B., Linz Ch, Duckstein H. Simulation of two-plane automatic balancing of a rigid rotor. Mathematics and Computers in Simulation, Vol. 58, Issues 4-6, 2002, p. 351-365.

Publisher
Ziyakaev G. R., Katanuhina S. L., Ponomarev A. V. The effect of friction on the accuracy of automatic balancing of unbalanced rotors. The World of Scientific Discoveries, Vol. 10, Issues 1(46), 2013, p. 104-108, (in Russian).

Search CrossRef
Gorbenko A. N. Influence of rotor unbalance increasing on the stability of its autobalancing. Procedia Engineering, Vol. 206, 2017, p. 266-271.

Publisher
Goncharov V. An increase of the balancing capacity of ball or roller-type auto-balancers with reduction of time of achieving auto-balancing. Eastern-European Journal of Enterprise Technologies. Vol. 1, Issue 7(85), 2017, p. 15-24.

Publisher
Strautmanis G., Mezītis M., Strautmane V. The impact of rotor elastic suspension settings on the acceleration of the automatic balancer compensating mass. Vibroengineering Procedia, Vol. 14, 2017, p. 13-17.

Publisher
Strautmanis G. On the stability of the autobalancing conditions of a ball autoequalizer. Scientific Journal of RTU/ Transport and Engineering/ Mechanics, Vol. 36, 2015, p. 31-34, (in Latvian).

Search CrossRef
Strautmanis G., Jurjevs V., Cokalo V. A Balancing Device for Centrifuges of Washing Machines. LV Patents, LV 14368 B, 2011, (in Latvian).

Search CrossRef
Shchukins I., Zakrzevskis M., Ivanov Y., et al. Application of software SPRING and method of complete bifurcation groups for the bifurcation analysis of nonlinear dynamical system. Journal of Vibroengineering, Vol. 10, Issue 4, 2008, p. 510-518.

Search CrossRef

Cited by

Research on Artificial Self-Recovery Technology in Engineering Practice

Xin Pan | Jingyi Liang | Dehong Ge | Jiaqiao Lu | Yunpeng Guo

(2024)

ICTE in Transportation and Logistics 2019

Guntis Strautmanis | Alexander Gorbenko | Mareks Mezitis | Valentina Strautmane | Pavels Stankevics

(2020)

About this article

Received

15 March 2019

Accepted

28 March 2019

Published

07 June 2019

SUBJECTS

Chaos, nonlinear dynamics and applications

DOI

https://doi.org/10.21595/vp.2019.20656

Keywords

automatic balancing device

operating regime

ball

rotor

area of attraction

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2021 01 31

Modelling of transient and steady-state modes of a vertical rotor with an automatic balancing device

Guntis Strautmanis, Gennadiy Filimonikhin, Mareks Mezitis, Alexander Gorbenko, Valentina Strautmane, Zura Sansyzbajeva

Research article

2020 11 05

Comparative analysis of rotor system models with auto-balancers of ball, roller and pendulum type

Gennadiy Filimonikhin, Guntis Strautmanis, Alexander Gorbenko, Mareks Mezitis, Irina Filimonikhina, Marina Gromova

Research article

2019 10 19

On the issue of acceleration of the compensating mass in an automatic balancing device with a horizontal axis of rotation

Guntis Strautmanis, Mareks Mezitis, Valentina Strautmane, Alexander Gorbenko

Research article

2019 06 25

Motion modes of the nonlinear mechanical system of the rotor autobalancer

Alexander Gorbenko, Guntis Strautmanis, Gennadiy Filimonikhin, Mareks Mezitis

G. Strautmanis, M. Mezitis, V. Strautmane, A. Gorbenko, I. Shchukins, and M. Gromova, “Study of the area of attraction of the auto-balancing mode in a ball-type automatic balancing device with a horizontal axis of rotation,” Vibroengineering PROCEDIA, Vol. 24, pp. 63–67, Jun. 2019, https://doi.org/10.21595/vp.2019.20656

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2019.20656
UR  - https://doi.org/10.21595/vp.2019.20656
TI  - Study of the area of attraction of the auto-balancing mode in a ball-type automatic balancing device with a horizontal axis of rotation
T2  - Vibroengineering PROCEDIA
AU  - Strautmanis, Guntis
AU  - Mezitis, Mareks
AU  - Strautmane, Valentina
AU  - Gorbenko, Alexander
AU  - Shchukins, Igors
AU  - Gromova, Marina
PY  - 2019
DA  - 2019/06/07
PB  - JVE International Ltd.
SP  - 63-67
VL  - 24
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Strautmanis_2019,
	doi = {10.21595/vp.2019.20656},
	url = {https://doi.org/10.21595/vp.2019.20656},
	year = 2019,
	month = {jun},
	publisher = {{JVE} International Ltd.},
	volume = {24},
	pages = {63--67},
	author = {Guntis Strautmanis and Mareks Mezitis and Valentina Strautmane and Alexander Gorbenko and Igors Shchukins and Marina Gromova},
	title = {Study of the area of attraction of the auto-balancing mode in a ball-type automatic balancing device with a horizontal axis of rotation},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]G. Strautmanis, M. Mezitis, V. Strautmane, A. Gorbenko, I. Shchukins, and M. Gromova, “Study of the area of attraction of the auto-balancing mode in a ball-type automatic balancing device with a horizontal axis of rotation,” Vibroengineering PROCEDIA, vol. 24, pp. 63–67, Jun. 2019, doi: 10.21595/vp.2019.20656.

Copy IEEE

Copied to clipboard!

Strautmanis, Guntis, Mareks Mezitis, Valentina Strautmane, Alexander Gorbenko, Igors Shchukins, and Marina Gromova. “Study of the Area of Attraction of the Auto-Balancing Mode in a Ball-Type Automatic Balancing Device with a Horizontal Axis of Rotation.” Vibroengineering PROCEDIA 24 (June 7, 2019): 63–67. https://doi.org/10.21595/vp.2019.20656.

Copy Chicago

Copied to clipboard!

Study of the area of attraction of the auto-balancing mode in a ball-type automatic balancing device with a horizontal axis of rotation

Abstract

Highlights

1. Introduction

2. Design model and mathematical model of a rotor with an ABD

3. Results of the research of the mathematical model

4. Conclusions

References

Cited by

About this article

Related Articles