Modelling of transient and steady-state modes of a vertical rotor with an automatic balancing device

Strautmanis, Guntis; Filimonikhin, Gennadiy; Mezitis, Mareks; Gorbenko, Alexander; Strautmane, Valentina; Sansyzbajeva, Zura

doi:10.21595/jve.2021.21804

Journal of Vibroengineering

Browse Journal

Submit article

Published: 31 January 2021

Check for updates

Modelling of transient and steady-state modes of a vertical rotor with an automatic balancing device

Guntis Strautmanis¹

Gennadiy Filimonikhin²

Mareks Mezitis³

Alexander Gorbenko⁴

Valentina Strautmane⁵

Zura Sansyzbajeva⁶

¹Riga Technical University, Riga, Latvia

²Central Ukrainian National Technical University, Kropyvnytskyi, Ukraine

³Transport Academy, Riga, Latvia

⁴Kerch State Maritime Technological University, Kerch, Russia

⁵Railway Transport Institute, Daugavpils, Latvia

⁶L. N. Gumilev Eurasian National University, Astana, Kazakhstan

Corresponding Author:

Guntis Strautmanis

Cite the article Download PDF

Downloads 1067

WoS Core Citations 1

CrossRef Citations 1

Abstract

The authors of the study work out the differential equations of motion of a vertical rotor model on an elastic-dissipative suspension, balanced by a ball-type automatic balancing device. Often, the cross-section of the cavity of the body of the automatic balancing device is rectangular and during rolling the balls have two points of contact, in one of which the balls slide along the surface of the cavity. To prevent the balls from sliding, the inner surface of the cavity of the automatic balancing device is made in the shape of a torus, which provides one point of contact. The forces of gravity and the forces of resistance to the movement of the correcting weights are taken into account, and the model is drawn up for both viscous and dry friction forces inside the body of the automatic balancing device. The obtained mathematical model of the rotor makes it possible to study the transient and steady-state modes of motion of the rotor system.

Modelling of transient and steady-state modes of a vertical rotor with an automatic balancing device

Highlights

The authors obtained a system of differential equations for a rotor system with a ball-type ABD, in which the inner space of the body is made in the shape of a torus, which provides a minimum resistance force to the motion of the ball and the best conditions for the location of balls in the auto-balancing mode.
The proposed system of differential equations makes it possible to proceed to the study of simpler rotor systems with a vertical axis of rotation, equipped with an ABD, in which the balls move in both longitudinal and transverse directions.
The system of differential equations makes it possible to investigate both steady-state modes of rotor motion and transient modes.

1. Introduction

One of the design stages of a rotor system with a ball-type automatic balancing device (ABD) is the development and substantiation of the design model of the rotor and its mathematical model. The advantage of this type of the ABD is that the balls themselves are set opposite to the rotor unbalance in the superresonance zone of the rotor motion frequency [1-3].

Most of the studies and publications are concerned with the consideration of the steady-state mode of rotor systems with ABD. At the same time, transient modes, although relatively short-lived, are accompanied by increased oscillation amplitudes. The role of the ABD in transient modes of the rotor system has not been studied to the full. This is due, inter alia, to the complexity of mathematical modelling not only of steady-state [5], but especially of transient processes [6].

In [15], it is indicated that in transient modes at insufficient engine power, the Sommerfeld effect may occur, in this case the ABD aggravates increased vibrations. In the scientific literature there are publications [21], where the issue of reducing resonant vibrations is considered by varying the parameters of the rotor system when installing the ABD. However, the influence of the ABD parameters on the possibility of reducing resonance amplitudes is insufficiently disclosed in the scientific literature. The elaboration of a mathematical model of a rotor with an ABD for a transient mode will allow further deeper and comprehensive study of this issue.

In scientific publications axisymmetric rotors on two isotropic [10] or anisotropic elastic supports [11, 13] are mainly considered. At the same time, a large number of rotor systems have a cantilever layout. In this case, in the motion of such rotor systems, both translational and angular oscillations are realized, which complicates both the derivation of the differential equations of motion and the analysis of the calculation results. At the same time, the elaboration of new and improvement of existing rotor systems requires the solution of such complex mathematical models. As a rule, such mathematical models imply their numerical integration, which requires the use of special software, in particular, the SPRING software described in [12] and allowing implementation of various research tasks.

In [16-19], it is mentioned that weights in the form of balls in the acceleration mode of the rotor and in the stationary mode roll along the ABD treadmill, at the same time it is indicated that the movement of weights in the ABD body occurs in the same plane (along the treadmill). When the ball rolls on the treadmill, the contact with the ABD body is provided at one point, which reduces the resistance force. In real conditions, during the acceleration of the rotor, the ball, for various reasons, inside the ABD body begins to move both along the treadmill and in the transverse direction, which can lead to the emergence of side steady modes that do not allow the ball to accelerate to the operating speed of the rotor. This is confirmed by mathematical modelling of the conditions for acceleration of the weight, considered in [6]. Thus, it becomes necessary to take into account the transverse motion of the ball in the mathematical model.

Cyclically alternating weights in rotor systems also require ensuring their fatigue strength. To check the strength of the rotor and ABD parts, one can, in particular, use the approach mentioned in [14].

When creating a mathematical model of a rotor system with an ABD, the laws of theoretical mechanics [4] and the theory of rotors with automatic balancing devices [7-9] were applied.

The aim of this work is to obtain a mathematical model of a cantilever rotor system with a ball-type ABD in transient and steady-state modes taking into account the longitudinal and transverse movements of the balls inside the ABD body.

2. Mechanical model of the rotor system

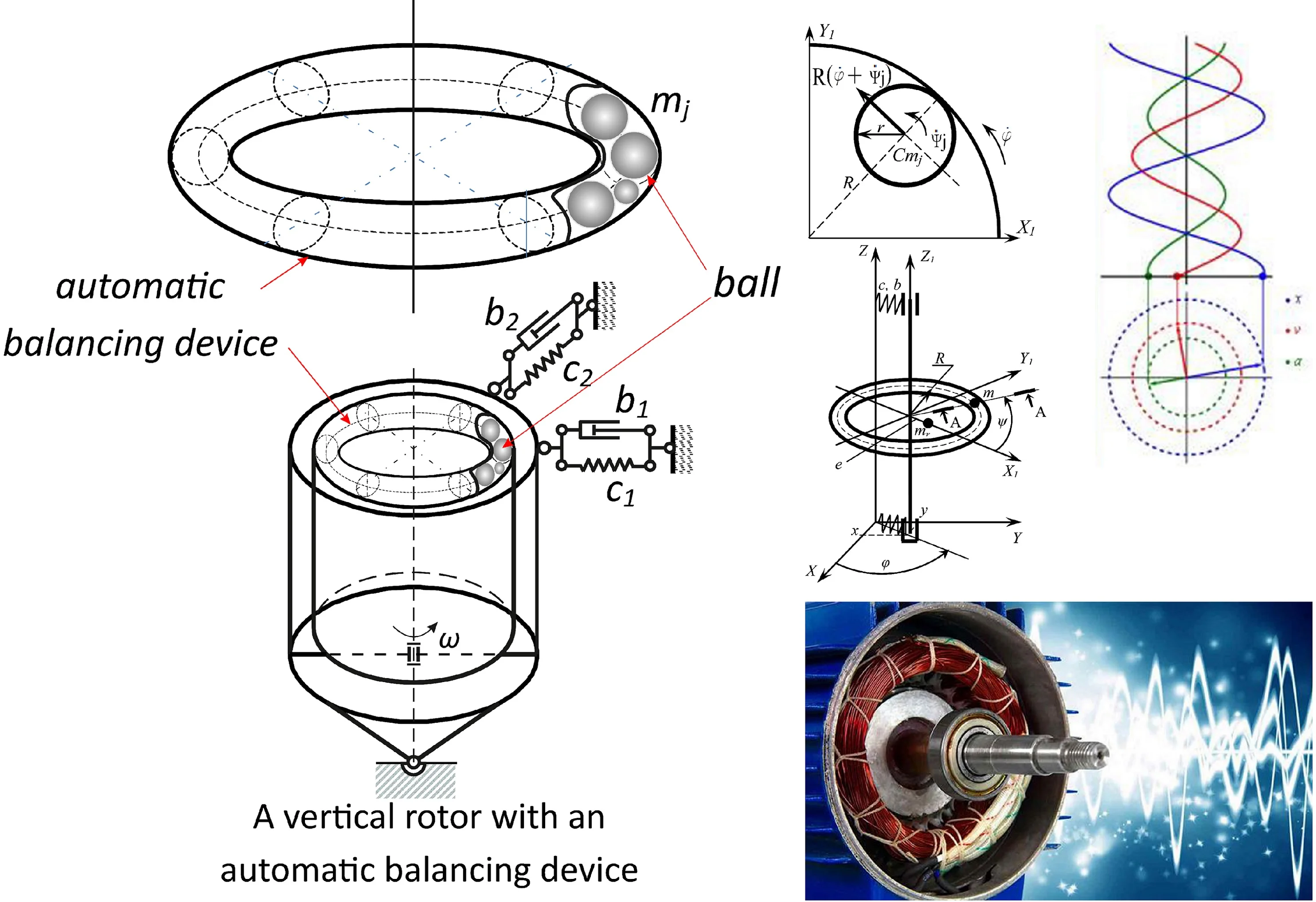
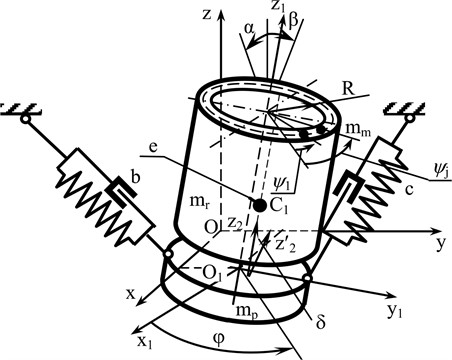
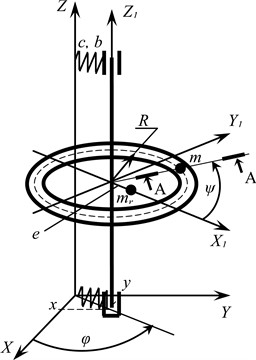
The rotor system consists of a platform, a rotor, and a ball-type ABD mounted on the rotor. The ABD contains $n$ identical balls of radius $r$ . The balls are inside a toroidal cavity (torus). The radius of the generating circumference of the torus is $R_{1}$ , and of the guide in the circumferential direction – $R$ .

The platform is fixed on elastic-viscous supports. The rotor oscillates along with the platform and rotates relative to the platform. The masses of the rotor, platform and one ball are, respectively, equal to $m_{r}$ , $m_{p}$ , $m$ .

The design model of the rotor system is shown in Fig. 1. The positions of the rotor system are determined by the following generalized coordinates:

– linear coordinates $x$ , $y$ , $z$ of the origin of the moving coordinate system $0_{1} x_{1} y_{1} z_{1}$ relative to the fixed system $0 x y z$ ;

– angular coordinates $α$ , $β$ , $θ$ (angles of inclination of the rotor axis in plane $0_{1} x_{1} z_{1}$ and $0_{1} y_{1} z_{1}$ , and the angle of twist around $z_{1}$ axis, respectively);

– angular coordinates $ψ_{j}$ , $γ_{j}$ , $/ j = \bar{1, n} /$ , determining the position of the center of $j$ ball in the ABD.

When deriving the equations of motion of the system, the assumptions are made that:

– linear and angular coordinates of the platform are sufficiently small $|x|$ , $|y|$ , $|z|$ , $|α|$ , $|β|$ , $|θ| ≪ 1$ and their time derivatives are small, too;

– balls roll on the surface of the torus without sliding.

The movement of compensating weights (balls) inside the torus is considered in two sections – in the circumferential and transverse directions.

The study of the steady-state mode of the rotor system is carried out at a constant angular velocity of the rotor rotation, i.e. $ω =$ const. The angle of the rotor rotation in this case is determined by the expression $φ = ω t$ . In the study of transient modes, the angular velocity of the rotor rotation changes and is a given function of time, i.e. $ω = f (t)$ .

Fig. 1Design model of the rotor system; a) general view; b) torus cross section

a)

b)

The tensors of the moments of inertia, characterizing the correspondingly distributed rotating $i$ masses of the rotor and the ABD body, as well as $m_{p}$ of the platform, have the form:

1

I_{i} = (\begin{matrix} I_{i x} & 0 & 0 \\ 0 & I_{i y} & 0 \\ 0 & 0 & I_{i z} \end{matrix}), I_{2} = (\begin{matrix} I_{2 x} & - I_{x_{2} y_{2}} & - I_{x_{2} z_{2}} \\ - I_{y_{2} x_{2}} & I_{2 y} & - I_{y_{2} z_{2}} \\ - I_{z_{2} x_{2}} & - I_{z_{2} y_{2}} & I_{2 z} \end{matrix}),

and $I_{x y} = I_{y x}$ ; $I_{x z} = I_{z x}$ ; $I_{y z} = I_{z y} .$

The radius vectors determining the position of the centers of the rotor masses (point $C_{1}$ ) and platform (point $C_{2}$ , not shown in Fig. 1), as well as $j$ ball in the ABD (points $C_{j}$ ) in the moving coordinate system $0_{1} x_{1} y_{1} z_{1}$ , have the following form:

2

{\bar{r}}_{1} = {\bar{i}}_{0} e \cos φ + {\bar{j}}_{0} e \sin φ + {\bar{k}}_{0} h, {\bar{r}}_{2} = {\bar{i}}_{0} r_{2 x} + {\bar{j}}_{0} r_{2 y} + {\bar{k}}_{0} r_{2 z},

3

{\bar{r}}_{j} = {\bar{i}}_{0} r_{j x} + {\bar{j}}_{0} r_{j y} + {\bar{k}}_{0} r_{j z}, j = 1, n,

where $φ$ – angle of the rotor rotation around its axis; $h$ – distance from the center of the rotor masses to the suspension plane (not shown in Fig. 1); $e$ – value of the static eccentricity of the rotor.

The differential equations of motion of the rotor system are obtained using the Lagrange equations of the 2nd kind, which have the form:

4

\frac{d}{d t} (\frac{\partial T}{\partial {\dot{q}}_{i}}) - \frac{\partial (T - Π)}{\partial q_{i}} + \frac{\partial R_{d}}{\partial {\dot{q}}_{i}} = Q_{i},

where $T$ – kinetic energy of the rotor system; $П$ – potential energy of the system; $R_{d}$ – dissipative function in generalized coordinates; $Q_{i}$ – generalized strength.

The kinetic energy of the rotor system is made up of the energy of rotating $T_{1}$ and non-rotating parts of the rotor $T_{2}$ , as well as the kinetic energy of the balls $T_{m}$ :

5

T = T_{1} + T_{2} + T_{m},

where $T_{1}$ – kinetic energy of the rotating parts of the rotor; $T_{2}$ – non-rotating parts of the rotor; $T_{m}$ – kinetic energy of the balls.

The kinetic energy of the rotating parts of the rotor has two components, caused by the translational movement of the rotor with the center of masses (point $C_{1}$ ) and the rotational movement of the rotor around the center of masses [6], and is expressed by the equation:

6

T_{1} = \frac{m_{1} V_{C_{1}}^{2}}{2} + T_{1 r o t},

where $V_{C_{1}}$ – absolute velocity of the center of masses of the rotor; $T_{1 r o t}$ – kinetic energy of the rotational motion of the rotor relative to its center of masses.

The position of the center of masses of rotor $C_{1}$ in the fixed coordinate system $0 x y z$ is determined by the expression:

7

{\bar{r}}_{C_{1}} = \bar{r} + {\bar{r}}_{1},

where $\bar{r}$ – radius vector that determines the position of the origin of the moving coordinate system $0_{1} x_{1} y_{1} z_{1}$ ; ${\bar{r}}_{1}$ – radius vector that determines the position of the center of masses of the rotor in the moving coordinate system $0_{1} x_{1} y_{1} z_{1}$ in relative motion.

The absolute velocity of the center of the rotor masses after transformation is determined by:

8

{\bar{V}}_{C_{1}} = \frac{d {\bar{r}}_{C_{1}}}{d t} = \bar{V} + {\bar{V}}_{r} + \bar{Ω} \times {\bar{r}}_{1},

where:

9

\bar{V} = \frac{d \bar{r}}{d t} = \bar{i} \dot{x} + \bar{j} \dot{y} + \bar{k} \dot{z},

10

{\bar{V}}_{r} = \frac{d {\bar{r}}_{1}}{d t} = {\bar{i}}_{0} (- e \dot{φ} \sin φ) + {\bar{j}}_{0} (e \dot{φ} \cos φ),

11

\bar{Ω} = \bar{i} (\dot{β} + \dot{Θ} α) + \bar{j} (\dot{α} - \dot{Θ} β) + \bar{k} (\dot{Θ} + \dot{α} β - \dot{β} α) = \bar{i} Ω_{x} + \bar{j} Ω_{y} + \bar{k} Ω_{z},

12

\bar{Ω} \times {\bar{r}}_{1} = \bar{i} (- Ω_{z} e \sin φ) + \bar{j} (Ω_{z} e \cos φ) + \bar{k} (Ω_{x} e \sin φ - Ω_{x} e \cos φ),

where $\bar{Ω}$ – vector of the angular velocity of the rotor in the moving coordinate system $0_{1} x_{1} y_{1} z_{1}$ when it moves relative to pole $0_{1}$ .

The transfer matrix for the transition to the fixed coordinate system $0 x y z$ is obtained by multiplying the rotation matrices of the moving coordinate system $0_{1} x_{1} y_{1} z_{1}$ relative to the fixed one:

13

V_{1} = V_{x y} ∙ V_{z} = (\begin{matrix} \cos α & 0 & - \sin α \\ 0 & \cos β & \sin β \\ \sin α & - \sin β & \cos α \cos β \end{matrix}) ∙ (\begin{matrix} \cos θ & \sin θ & 0 \\ - \sin θ & \cos θ & 0 \\ 0 & 0 & 1 \end{matrix}) .

Taking into account the smallness of the rotor vibration angles, rotation matrix $V_{1}$ takes the form:

14

V_{1} = (\begin{matrix} 1 & θ & - α \\ - θ & 1 & β \\ α & - β & 1 \end{matrix}) .

Multiplying Eqs. (10) and (12) by the rotation matrix $V_{1}$ Eqs. (14), taking into account Eqs. (9), we obtain in the final form the velocity vector of the center of masses of the rotor:

15

{\bar{V}}_{C_{1}} = \bar{i} (\dot{x} - e \dot{θ} \sin φ - e \dot{φ} \sin φ) + \bar{j} (\dot{y} + e \dot{θ} \cos φ + e \dot{φ} \cos φ)

+ \bar{k} (\dot{z} + e \dot{α} \sin φ - e \dot{β} \cos φ) .

The expression for the kinetic energy of the rotor in relative motion is obtained taking into account the transition matrix from the central axes of the rotor $C_{1} x_{2} y_{2} z_{2}$ to the main central axes $C_{1} x_{2}^{'} y_{2}^{'} z_{2}^{'}$ . Due to the fact that the inertia moments of the rotor relative to the axes $C_{1} x_{2}$ and $C_{1} y_{2}$ are equal to each other, the couple unbalance of the rotor is determined by angle $δ$ , and the proper rotation of the rotor is determined by angle $φ$ , the rotation matrices have the form:

16

V_{φ} = (\begin{matrix} \cos φ & \sin φ & 0 \\ - \sin φ & \cos φ & 0 \\ 0 & 0 & 1 \end{matrix}), V_{δ} = (\begin{matrix} \cos δ & 0 & - \sin δ \\ 0 & 1 & 0 \\ \sin δ & 0 & \cos δ \end{matrix}) .

Transition matrix $V_{2}$ is obtained by multiplying rotation matrices $V_{φ}$ and $V_{δ}$ and, taking into account the smallness of angle $δ$ , it takes the following form:

17

V_{2} = (\begin{matrix} \cos φ \cos δ & \sin φ \cos δ & - \sin δ \\ - \sin φ & \cos φ & 0 \\ \cos φ \sin δ & \sin φ \sin δ & \cos δ \end{matrix}) or V_{2} = (\begin{matrix} \cos φ & \sin φ & - δ \\ - \sin φ & \cos φ & 0 \\ δ cos φ & δ sin φ & 1 \end{matrix}) .

The angular velocity vector, taking into account its own rotation in the moving coordinate system $C_{1} x_{2} y_{2} z_{2}$ , has the following form:

18

{\bar{Ω}}_{1} = {\bar{i}}_{0} (\dot{β} + \dot{Θ} α) + {\bar{j}}_{0} (\dot{α} - \dot{Θ} β) + {\bar{k}}_{0} (\dot{φ} + \dot{Θ} + \dot{α} β - \dot{β} α) .

Multiplying Eqs. (18) by (17), we obtain the vector of the angular rotor velocity when it moves relative to the center of masses in a moving coordinate system associated with the main central axes of inertia $C_{1} x_{2}^{'} y_{2}^{'} z_{2}^{'}$ , i.e. ${\tilde{Ω}}_{1} = V_{2} {\bar{Ω}}_{1} .$ Then, the kinetic energy of the rotor in relative motion is determined by the expression:

19

T_{1 r o t} = \frac{{\tilde{Ω}}_{1} I_{1} {\tilde{Ω}}_{1}}{2} .

The total kinetic energy $T_{1}$ of the rotor, taking into account Eqs. (6) and (19), takes the form:

20

T_{1} = 0,5 m_{1} [{(\dot{x} - e \dot{φ} \sin φ - e \dot{θ} \sin φ)}^{2} + {(\dot{y} + e \dot{φ} \cos φ + e \dot{θ} \cos φ)}^{2}

+ {(\dot{z} + e \dot{α} \sin φ - e \dot{β} \cos φ)}^{2}] + 0,5 I_{x 1} ({\dot{α}}^{2} + {\dot{β}}^{2} + 2 δ \dot{φ} \dot{α} \cos φ + 2 δ \dot{θ} \dot{α} \cos φ

- 2 δ \dot{φ} \dot{β} \sin φ - 2 δ \dot{θ} \dot{β} \sin φ + 2 β \dot{α} \dot{θ} - 2 α \dot{β} \dot{θ}) + 0,5 I_{z 1} ({\dot{φ}}^{2} + {\dot{θ}}^{2} + 2 δ \dot{φ} \dot{β} \sin φ

- 2 δ \dot{φ} \dot{α} \cos φ + 2 δ \dot{θ} \dot{β} \sin φ - 2 δ \dot{θ} \dot{α} \cos φ + 2 α \dot{β} \dot{φ} - 2 β \dot{α} \dot{φ} + 2 \dot{φ} \dot{θ} + 2 α \dot{β} \dot{θ} - 2 β \dot{α} \dot{θ}),

where $I_{x 1} = I_{y 1}$ – moment of inertia of the rotor relative to axes $x_{1}$ or $y_{1}$ ; $I_{z 1}$ – moment of inertia of the rotor relative to $z_{1}$ axis.

The kinetic energy of ball $T_{m_{j}}$ is determined in a similar way. The ball participates simultaneously in two motions in the circumferential and cross sections [3]:

- in a translational motion of the ball with a center of masses (point $C_{m_{j}}$ )

– in a rotational motion around the center of masses.

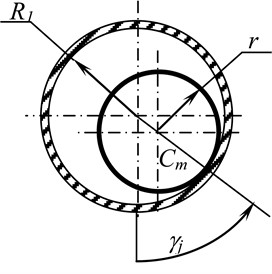
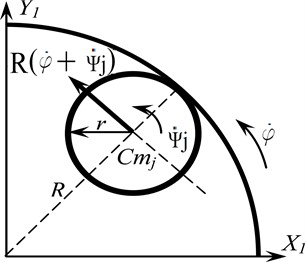
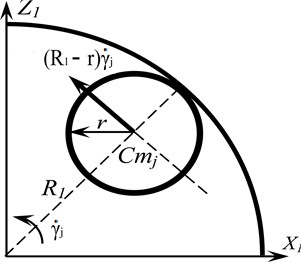
The design model for determining the kinetic energy of the weights is shown in Fig. 2:

21

T_{m j} = \frac{m_{m} V_{C_{m j}}^{2}}{2} + \frac{J_{C_{m j}} ω_{j}^{2}}{2},

where ${\dot{ω}}_{j} = \dot{φ} + {\dot{ψ}}_{j}$ – absolute velocity of the ball in the circumferential plane; ${\dot{ω}}_{j} = {\dot{γ}}_{j}$ – absolute velocity of the ball in the transverse plane.

Fig. 2Rolling pattern without sliding the ball on the ball raceway; a) in the circumferential plane, b) in the transverse plane

a)

b)

If we neglect the displacements of rotor $z$ along the axis of rotation and rotational vibration $θ$ around the same axis, due to their smallness and negligible effect on the transverse vibrations of the rotor, the kinetic energy of the entire rotor system takes the following form:

22

T = 0,5 m_{1} [{(\dot{x} - e \dot{φ} \sin φ)}^{2} + {(\dot{y} + e \dot{φ} \cos φ)}^{2} + 0,5 I_{x 1} ({\dot{α}}^{2} + {\dot{β}}^{2} + 2 δ \dot{φ} \dot{α} \cos φ

- 2 δ \dot{φ} \dot{β} \sin φ) + 0,5 I_{z 1} ({\dot{φ}}^{2} + 2 δ \dot{φ} \dot{β} \sin φ - 2 δ \dot{φ} \dot{α} \cos φ + 2 α \dot{β} \dot{φ} - 2 β \dot{α} \dot{φ})

+ 0,5 m_{2} ({\dot{x}}^{2} + {\dot{y}}^{2}) + 0,5 m_{m} \sum_{1}^{n} \{{\dot{x}}^{2} + {\dot{y}}^{2} + R^{2} [{(\dot{φ} + {\dot{ψ}}_{j})}^{2} + {\dot{β}}^{2} \cos^{2} (φ + ψ_{j})

+ {\dot{α}}^{2} \sin^{2} (φ + ψ_{j}) - 2 β \dot{β} (\dot{φ} + {\dot{ψ}}_{j}) \sin (φ + ψ_{j}) \cos (φ + ψ_{j}) - 2 \dot{α} \dot{β} \sin (φ + ψ_{j})

\times \cos (φ + ψ_{j}) + 2 α \dot{α} (\dot{φ} + {\dot{ψ}}_{j}) \sin (φ + ψ_{j}) \cos (φ + ψ_{j}) + 2 β \dot{α} (\dot{φ} + {\dot{ψ}}_{j})

\times \sin^{2} (φ + ψ_{j}) - 2 α \dot{β} (\dot{φ} + {\dot{ψ}}_{j}) \cos^{2} (φ + ψ_{j})] + 2 R (\dot{φ} + {\dot{ψ}}_{j}) [\dot{y} \cos (φ + ψ_{j})

- \dot{x} \sin (φ + ψ_{j})] + 2 (R_{1} - r) {\dot{γ}}_{j} [\dot{x} \cos (φ + ψ_{j}) + \dot{y} \sin (φ + ψ_{j})] \cos γ_{j}

+ {(R_{1} - r)}^{2} {\dot{γ}}_{j}^{2}\} + 0,2 m_{m} \sum_{1}^{n} [{\dot{ψ}}_{j}^{2} R^{2} + {(R_{1} - r)}^{2} {\dot{γ}}_{j}^{2}] .

When determining the potential energy of the system, its change due to the vertical displacement of the center of the rotor masses is not taken into account. In addition, when determining the potential energy of the balls, the angle of rotation of rotor axis $α$ and $β$ is not taken into account due to its smallness in comparison with angle $γ_{j}$ . The value of the potential energy of the rotor system is determined by the deformation of the elastic elements of the rotor suspension and the change in the position of the center of masses of the compensating weights (balls):

23

Π = 0,5 \sum c_{i} Δ_{i}^{2} + m_{m} g (R_{1} - r) \sum_{1}^{n} (1 - \cos γ_{j}),

where $c_{i}$ – stiffness of $i$ elastic element along its axis; $Δ_{i}$ – value of deformation of $i$ elastic element; $r$ – radius of the ball; $R_{1}$ – radius of the torus cross-section.

The impact of dissipative forces in the elastic-dissipative suspension of the rotor system is taken into account by introducing equivalent viscous friction. According to the hypothesis of dissipative forces, the resistance of the medium is taken proportional to the generalized velocities of translational and angular displacements. In accordance with the hypothesis, the dissipative function in the elastic suspension has the following form:

24

R^{*} = 0,5 \sum b_{i} {\dot{q}}_{i}^{2},

where $b_{i}$ – dissipation coefficient of $i$ suspension element; ${\dot{q}}_{i}$ – value of the generalized velocity of $i$ element.

Dissipative forces in the ABD can be modelled through the forces of dry and / or viscous rolling friction. It is assumed that the ball, when moving relative to the body, moves without slipping and without separation from the body. In this case, the moment of friction forces acting on the ball is equal to:

– dry rolling friction:

25

M_{ψ_{j}} = \frac{N_{j} k (R + R_{1} \sin γ_{j})}{r}, M_{γ_{j}} = \frac{N_{j} k R_{1}}{r},

where $N_{j}$ – reaction force from the pressure of $i$ ball on the inner surface of the torus; $k$ – rolling friction coefficient;

– viscous friction:

26

M_{ψ_{j}} = \frac{b_{r} {\dot{ψ}}_{j} (R + R_{1} \sin γ_{j})}{r}, M_{γ_{j}} = \frac{b_{r} {\dot{γ}}_{j} R_{1}}{r},

where $b_{r}$ – dissipation coefficient for viscous friction in the ABD.

Force $N_{j}$ without taking into account the accelerations, which are small in comparison with the centripetal acceleration of the ball, is determined from the expression:

27

N_{j} = m_{m} [g \cos γ_{j} + {\dot{γ}}_{j}^{2} (R_{1} - r) + R {(\dot{φ} + {\dot{ψ}}_{j})}^{2}] .

After transformations, in accordance with Eqs. (4), we obtain a system of differential equations for a rotor system with a vertical axis of rotation with a ball-type ABD:

1) For $x, y$ :

28

M \ddot{x} + M H \ddot{α} + b_{1} \dot{x} + c_{1} x - m_{m} \sum_{1}^{n} \{R [{(\dot{φ} + {\dot{ψ}}_{j})}^{2} \sin (φ + ψ_{j})

+ (\ddot{φ} + {\ddot{ψ}}_{j}) \cos (φ + ψ_{j})] + (R_{1} - r) ({\ddot{γ}}_{j} \cos γ - {\dot{γ}}_{j}^{2} \sin γ_{j}) \cos (φ + ψ_{j})

- 2 (R_{1} - r) {\dot{γ}}_{j} (\dot{φ} + {\dot{ψ}}_{j}) \sin (φ + ψ_{j}) \cos γ_{j}\} = m_{1} e ({\dot{φ}}^{2} \cos φ + \ddot{φ} \sin φ),

29

M \ddot{y} - M H \ddot{β} + b_{2} \dot{y} + c_{2} y - m_{m} \sum_{1}^{n} \{R [{(\dot{φ} + {\dot{ψ}}_{j})}^{2} \cos (φ + ψ_{j})

- (\ddot{φ} + {\ddot{ψ}}_{j}) \sin (φ + ψ_{j})] + (R_{1} - r) ({\ddot{γ}}_{j} \cos γ_{j} - {\dot{γ}}_{j}^{2} \sin γ_{j}) \sin (φ + ψ_{j})

+ 2 (R_{1} - r) {\dot{γ}}_{j} (\dot{φ} + {\dot{ψ}}_{j}) \cos (φ + ψ_{j}) \cos γ_{j}\} = m_{1} e ({\dot{φ}}^{2} \sin φ - \ddot{φ} \cos φ)

2) For $α$ , $β$ :

30

I_{x 1} \ddot{α} - I_{z 1} (\ddot{φ} β + \dot{φ} \dot{β}) + b_{3} \dot{α} + c_{3} α + m_{m} R^{2} \sum_{1}^{n} \{[(\ddot{φ} + {\ddot{ψ}}_{j}) α - 2 (\dot{φ} + {\dot{ψ}}_{j}) \dot{α} - \ddot{β}]

\times \sin (φ + ψ_{j}) \cos (φ + ψ_{j}) - {(\dot{φ} + {\dot{ψ}}_{j})}^{2} [α \cos 2 (φ + ψ_{j}) + β \sin 2 (φ + ψ_{j})]

- [(\ddot{φ} + {\ddot{ψ}}_{j}) β + (\dot{φ} + {\dot{ψ}}_{j}) \dot{β} - \ddot{α}] \sin^{2} (φ + ψ_{j})\} = δ (I_{x 1} - I_{z 1}) (\ddot{φ} \sin φ + {\dot{φ}}^{2} \cos φ),

31

I_{y 1} \ddot{β} + I_{z 1} (\ddot{φ} α + \dot{φ} \dot{α}) + b_{4} \dot{β} + c_{4} β + m_{m} R^{2} \sum_{1}^{n} \{[(\ddot{φ} + {\ddot{ψ}}_{j}) β + 2 (\dot{φ} + {\dot{ψ}}_{j}) \dot{β} - \ddot{α}]

\times \sin (φ + ψ_{j}) \cos (φ + ψ_{j}) - {(\dot{φ} + {\dot{ψ}}_{j})}^{2} [α \sin 2 (φ + ψ_{j}) - β \cos 2 (φ + ψ_{j})]

+ [(\ddot{φ} + {\ddot{ψ}}_{j}) α + (\dot{φ} + {\dot{ψ}}_{j}) \dot{α} + \ddot{β}] \cos^{2} (φ + ψ_{j})\} = δ (I_{y 1} - I_{z 1}) (\ddot{φ} \cos φ - {\dot{φ}}^{2} \sin φ) .

3) For $ψ_{j}$ , $γ_{j}$ :

32

m_{m} R^{2} (\ddot{φ} + \frac{7}{5} {\ddot{ψ}}_{j}) + m_{m} R \{[2 (R_{1} - r) (\dot{φ} + {\dot{ψ}}_{j}) {\dot{γ}}_{j} \cos γ_{j} - \ddot{x} \sin (φ + ψ_{j})

+ \ddot{y} \cos (φ + ψ_{j})] + R [(α \ddot{α} - β \ddot{β}) \sin (φ + ψ_{j}) \cos (φ + ψ_{j}) + β \ddot{α} \sin^{2} (φ + ψ_{j})

- α \ddot{β} \cos^{2} (φ + ψ_{j})]\} + M_{ψ_{j}} = 0, j = 1, n,

33

\frac{7}{5} m_{m} {(R_{1} - r)}^{2} {\ddot{γ}}_{j} + m_{m} (R_{1} - r) \{[\ddot{x} \cos (φ + ψ_{j}) + \ddot{y} \sin (φ + ψ_{j})] \cos γ_{j}

- R {(\dot{φ} + {\dot{ψ}}_{j})}^{2} \cos γ_{j} + g \sin γ_{j} - R [{\dot{β}}^{2} \cos^{2} (φ + ψ_{j}) - {\dot{α}}^{2} \sin^{2} (φ + ψ_{j})] \cos γ_{j}

+ 2 R (\dot{φ} + {\dot{ψ}}_{j}) [\dot{β} \cos (φ + ψ_{j}) - \dot{α} \sin (φ + ψ_{j})] [β \sin (φ + ψ_{j}) - α \cos (φ + ψ_{j})]

\times \cos γ_{j} + 2 R \dot{α} \dot{β} \sin (φ + ψ_{j}) \cos (φ + ψ_{j}) \cos γ_{j}\} + M_{γ_{j}} = 0, j = 1, n .

4) For $φ$ . With a sufficiently large value of the engine torque $M_{r o t}$ on the rotor shaft, in a first approximation, the following conditions for changing the angular velocity can be accepted:

34

I_{z 1} \ddot{φ} = \{\begin{matrix} M_{r o t}, \dot{φ} < ω_{0}, \\ 0, \dot{φ} = ω_{0}, \end{matrix}

where $I_{z 1}$ – moment of inertia of the rotor system relative to the axis of rotation; $ω_{0}$ – operating angular velocity of the rotor.

The system of differential Eqs. (28-34) describes the motion of the rotor system in transient and steady-state modes.

This system of equations can be used to study other rotor systems with ball-type ABDs, in particular, a symmetric rotor on two supports with a symmetric or asymmetric suspension [8, 13]. At the same time, comparing the system of differential equations of a symmetric vertical rotor with the system of differential equations proposed in this work, one can state their complete coincidence provided there is exclusion from the system of angular coordinates for the rotor axis.

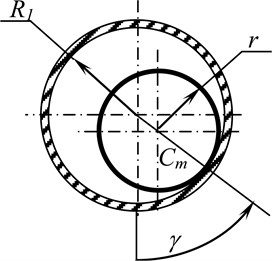
As an example, a system of differential equations for the design model of the rotor from [8] is given, which is obtained from the system of differential Eqs. (28-34) under the following conditions: $α = β = \dot{α} = \dot{β} = \ddot{α} = \ddot{β} = 0$ ; $\ddot{φ} = 0$ ; $j = 1 .$ Fig. 3 shows a design model of a vertical symmetrical rotor with a torus-shaped automatic balancer:

35

M \ddot{x} + b_{1} \dot{x} + c_{1} x - m_{m} \{R [{(\dot{φ} + \dot{ψ})}^{2} \sin (φ + ψ) + \ddot{ψ} \cos (φ + ψ)]

+ (R_{1} - r) (\ddot{γ} \cos γ - {\dot{γ}}^{2} \sin γ) \cos (φ + ψ) - 2 (R_{1} - r) \dot{γ} (\dot{φ} + \dot{ψ}) \sin (φ + ψ) \cos γ\}

= m_{1} e ({\dot{φ}}^{2} \cos φ),

36

M \ddot{y} + b_{2} \dot{y} + c_{2} y - m_{m} \{R [{(\dot{φ} + \dot{ψ})}^{2} \cos (φ + ψ) - \ddot{ψ} \sin (φ + ψ)]

+ (R_{1} - r) (\ddot{γ} \cos γ - {\dot{γ}}^{2} \sin γ) \sin (φ + ψ) + 2 (R_{1} - r) \dot{γ} (\dot{φ} + \dot{ψ}) \cos (φ + ψ) \cos γ\}

= m_{1} e ({\dot{φ}}^{2} \sin φ),

37

m_{m} R^{2} (\frac{7}{5} \ddot{ψ}) + m_{m} R [2 (R_{1} - r) (\dot{φ} + \dot{ψ}) \dot{γ} \cos γ - \ddot{x} \sin (φ + ψ) + \ddot{y} \cos (φ + ψ)]

+ M_{ψ} = 0,

38

\frac{7}{5} m_{m} {(R_{1} - r)}^{2} \ddot{γ} + m_{m} (R_{1} - r) [\ddot{x} \cos (φ + ψ) + \ddot{y} \sin (φ + ψ)] \cos γ

- m_{m} R (R_{1} - r) {(\dot{φ} + \dot{ψ})}^{2} \cos γ + m_{m} (R_{1} - r) g \sin γ + M_{γ} = 0 .

On the basis of the system of differential Eqs. (35-38), in particular, numerical calculations of the effect of the ball size on its acceleration in the autobalancing mode were carried out using the SPRING software [12], which is confirmed by field experiments [6, 22].

Fig. 3Design model of the rotor system; a) general view; b) torus cross section

a)

b)

3. Conclusions

The authors obtained a system of differential equations for a rotor system with a ball-type ABD, in which the inner space of the body is made in the shape of a torus, which provides a minimum resistance force to the motion of the ball and the best conditions for the location of balls in the auto-balancing mode.

The proposed system of differential equations makes it possible to proceed to the study of simpler rotor systems with a vertical axis of rotation, equipped with an ABD, in which the balls move in both longitudinal and transverse directions. The authors carried out a physical experiment with such a rotor system and a vertical axis of rotation. The results of the experiment completely coincided with mathematical modelling in the SPRING environment, thereby confirming the correctness of the proposed differential equations.

The system of differential equations makes it possible to investigate both steady-state modes of rotor motion and transient modes, as well as to study the stability areas of various modes of movement of ABD weights and select the parameters of the rotor system.

It is possible to model the force of resistance to the motion of the ball both by dry rolling friction and by viscous friction, which depends on the velocity of the ball.

References

Gorbenko A., Strautmanis G., Filimonikhin G., Mezītis M. Motion Modes of the Nonlinear Mechanical System of the Rotor Autobalancer. Vibroengineering Procedia, Vol. 25, Issues 1, 2019, p. 1-6.

Publisher
Nesterenko V. P. Automatic elimination by balls of static imbalance of the rotor of a two-mass system. University News. Engineering, Vol. 3, 1983, p. 46-50, (in Russian).

Search CrossRef
Strautmanis G., Mezitis M., Strautmane V., Gorbenko A. Model of a vertical rotor with an automatic balancer with two compensating masses. Vibroengineering Procedia, Vol. 21, Issue 1, 2018, p. 202-207.

Publisher
Strauch D. Classical Mechanics. An Introduction. Springer-Verlag, Berlin Heidelberg, 2009.

Publisher
Gorbenko A. N., Shmelev S. Kh. Necessary self-balancing robustness conditions for a two-bearing rotor taking unbalance mass into account. Herald of the Bauman Moscow State Technical University. Series Mechanical Engineering, Vol. 5, Issue 122, 2018, p. 36-50.

Publisher
Gorbenko A., Mezītis M., Strautmane V., Strautmanis G. The impact of an elastic rotor suspender and the size of the compensating mass on the acceleration of the automatic balancer. Procedia Computer Science, Vol. 149, Issue 2019, 2018, p. 301-306.

Publisher
Goncharov V. V., Filimonikhin G. B. Form and structure of differential equations of motion and process of auto-balancing in the rotor machine with auto-balancers. Bulletin of the Tomsk Polytechnic University, Geo Assets Engineering, Vol. 326, Issue 12, 2015, p. 20-30.

Search CrossRef
Strautmanis G., Mezitis M., Strautmane V. Model of a vertical rotor with a ball-type automatic balancer. Vibroengineering Procedia, Vol. 8, 2016, p. 57-62.

Search CrossRef
Gorbenko A. N., Klimenko N. P., Strautmanis G. Influence of rotor unbalance increasing on its autobalancing stability. Procedia Engineering, Vol. 206, 2017, p. 266-271.

Publisher
Sperling L., Ryzhik B., Duckstein H. Single-plain auto-balancing of rigid rotors. Technische Mechanik, Vol. 24, Issue 1, 2004, p. 1-24.

Search CrossRef
Sperling L., Ryzhik B., Duckstein H. Single-plain auto-balancing of anisotropically supported rigid rotors. Technische Mechanik, Vol. 24, Issue 1, 2004, p. 37-50.

Search CrossRef
Ščukins I., Zakrževskis M., Ivanov Y., et. al. Application of software SPRING and method of complete bifurcation groups for the bifurcation analysis of nonlinear dynamical system. Journal of Vibroengineering, Vol. 10, Issue 4, 2008, p. 510-518.

Search CrossRef
Strautmanis G., Mezītis M., Strautmane V., Gorbenko A. On the issue of impact of anisotropy of the rotor elastic suspension on the performance of the automatic balancer. Vibroengineering Procedia, Vol. 17, Issue 1, 2019, p. 1-6.

Publisher
Evseev D., Medvedev B., Medvedev P., Strautmanis G., Samoshkin S. Acoustic emission approach to determining survivability in fatigue tests. Procedia Computer Science, Vol. 149, 2019, p. 282-287.

Publisher
Yatsun V., Filimonikhina I., Podoprygora N., Hurievska O. Motion equations of the single-mass vibratory machine with a rotary-oscillatory motion of the platform and the form of a passive auto-balancer. Eastern-European Journal of Enterprise Technologies, Vol. 6, Issues 7(96), 2018, p. 58-67.

Publisher
Goncharov V. V., Filimonikhin G. B. Form and structure of differential equations of motion and process of autobalancing in the rotor machine with auto-balancers. Bulletin of the Tomsk Polytechnic University. Georesource Engineering, Vol. 326, Issue 12, 2015, p. 19-30, (in Russian).

Search CrossRef
Filimonikhin G., Yatsun V., Filimonikhina I., Ienina I., Munshtukov I. Studyng the load jam modes within the frame work of a flat model of the rotor with an autobalancer. Eastern-European Journal of Enterprise Technologies, Vol. 5, Issues 7(101), 2019, p. 51-61.

Publisher
Bykov V. G., Kovachev A. S. Dynamic of statically unbalanced rotor with eccentric ball autobalancer. Bulletin of St. Petersburg State University, Vol. 1, Issue 1, 2014, p. 579-588, (in Russian).

Search CrossRef
Green K., Friswell M. I., Champneys A. R., Lieven N. A. J. The stability of automatic ball balancers. 7th IFToMM-Conference on Rotor Dynamics, Vienna, Austria, 2006.

Search CrossRef
Adolfsson J. Passive Control of Mechanical Systems. Bipedal Walking and Autobalancing. Department of Mechanics. Royal Institute of Technology, S-10044 Stockholm, Sweden, 2001.

Search CrossRef
Ding H.,Li M., Fu H., Li M. The impact of rotor elastic suspension setting on the acceleration of the automatic balancer compensating mass. Recent Patents on Mechanical Engineering, Vol. 11, Issue 3, 2018, p. 232-241.

Publisher
Yatsun V., Filimonikhin G., Haleeva A., Krivoblotsky L., Machok Y., Mezitis M., Podoprygora N., Sadovyi M., Strautmanis G. Searching for the two frequency motion modes of a three-mass vibratory machine with a vibration exciter in the form of a passive auto-balancer. Eastern-European Journal of Enterprise Technologies, Vol. 4, Issues 7(106), 2020, p. 103-111.

Publisher

Cited by

The Inertial Disturbances of Fluid Movement in the Chamber of a Liquid Autobalancer

Vasyl Lozynskyi | Thaer Shihab | Ilona Drach | Liubomyr Ropyak

(2024)

About this article

Received

15 November 2020

Accepted

05 January 2021

Published

31 January 2021

SUBJECTS

System dynamics in manufacturing system modeling

DOI

https://doi.org/10.21595/jve.2021.21804

Keywords

rotor

automatic balancing device

equations of motion

elastic element

dissipation coefficient

transient mode

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous

Research article

2019 10 19

On the issue of acceleration of the compensating mass in an automatic balancing device with a horizontal axis of rotation

Guntis Strautmanis, Mareks Mezitis, Valentina Strautmane, Alexander Gorbenko

Research article

2019 06 25

Motion modes of the nonlinear mechanical system of the rotor autobalancer

Alexander Gorbenko, Guntis Strautmanis, Gennadiy Filimonikhin, Mareks Mezitis

Research article

2019 06 07

Study of the area of attraction of the auto-balancing mode in a ball-type automatic balancing device with a horizontal axis of rotation

Guntis Strautmanis, Mareks Mezitis, Valentina Strautmane, Alexander Gorbenko, Igors Shchukins, Marina Gromova

Research article

2018 12 13

Model of a vertical rotor with an automatic balancer with two compensating masses

Guntis Strautmanis, Mareks Mezitis, Valentina Strautmane, Alexander Gorbenko

G. Strautmanis, G. Filimonikhin, M. Mezitis, A. Gorbenko, V. Strautmane, and Z. Sansyzbajeva, “Modelling of transient and steady-state modes of a vertical rotor with an automatic balancing device,” Journal of Vibroengineering, Vol. 23, No. 3, pp. 759–769, Jan. 2021, https://doi.org/10.21595/jve.2021.21804

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2021.21804
UR  - https://doi.org/10.21595/jve.2021.21804
TI  - Modelling of transient and steady-state modes of a vertical rotor with an automatic balancing device
T2  - Journal of Vibroengineering
AU  - Strautmanis, Guntis
AU  - Filimonikhin, Gennadiy
AU  - Mezitis, Mareks
AU  - Gorbenko, Alexander
AU  - Strautmane, Valentina
AU  - Sansyzbajeva, Zura
PY  - 2021
DA  - 2021/01/31
PB  - JVE International Ltd.
SP  - 759-769
IS  - 3
VL  - 23
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

@article{Strautmanis_2021,
	doi = {10.21595/jve.2021.21804},
	url = {https://doi.org/10.21595/jve.2021.21804},
	year = 2021,
	month = {jan},
	publisher = {{JVE} International Ltd.},
	volume = {23},
	number = {3},
	pages = {759--769},
	author = {Guntis Strautmanis and Gennadiy Filimonikhin and Mareks Mezitis and Alexander Gorbenko and Valentina Strautmane and Zura Sansyzbajeva},
	title = {Modelling of transient and steady-state modes of a vertical rotor with an automatic balancing device},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]G. Strautmanis, G. Filimonikhin, M. Mezitis, A. Gorbenko, V. Strautmane, and Z. Sansyzbajeva, “Modelling of transient and steady-state modes of a vertical rotor with an automatic balancing device,” Journal of Vibroengineering, vol. 23, no. 3, pp. 759–769, Jan. 2021, doi: 10.21595/jve.2021.21804.

Copy IEEE

Copied to clipboard!

Strautmanis, Guntis, Gennadiy Filimonikhin, Mareks Mezitis, Alexander Gorbenko, Valentina Strautmane, and Zura Sansyzbajeva. “Modelling of Transient and Steady-State Modes of a Vertical Rotor with an Automatic Balancing Device.” Journal of Vibroengineering 23, no. 3 (January 31, 2021): 759–69. https://doi.org/10.21595/jve.2021.21804.

Copy Chicago

Copied to clipboard!

Modelling of transient and steady-state modes of a vertical rotor with an automatic balancing device

Abstract

Highlights

1. Introduction

2. Mechanical model of the rotor system

3. Conclusions

References

Cited by

About this article

Related Articles