Modal analysis of sandwich panel with composite laminated faces

Kormanikova, Eva

doi:10.21595/vp.2019.20658

Vibroengineering Procedia

Browse Procedia

Published: 25 April 2019

Check for updates

Modal analysis of sandwich panel with composite laminated faces

Eva Kormanikova¹

¹Department of Structural Mechanics, Technical University of Kosice, Košice, Slovakia

Cite the article Download PDF

Downloads 1339

CrossRef Citations 3

Abstract

A sandwich panel with laminate faces was used for free vibration analysis. The Shear Deformation Theory is considered for analysis. The effect of sandwich design parameters such as core thickness and fiber reinforced angle on vibration response is investigated. The modal analysis for various lengths of sandwich panel is done to find the limit length of the panel, which is sensitive to dynamic wind load.

Highlights

A sandwich panel with laminate faces
Free vibration analysis
The Shear Deformation Theory
The effect of sandwich design parameters on vibration response
The limit length of the panel
Sensitivity to dynamic wind load

1. Introduction

Sandwich panels are one of very important group of laminated composites. They consist of two thin faces with thickness of $h_{1}$ and $h_{3}$ and a core with thickness of $h_{2}$ . The faces are made of high strength materials having good properties under tension, such as fiber reinforced polymer matrix laminates used in this paper, while the core is made of lightweight materials such as foam, having good properties under compression. Sandwich composites combine lightness and flexural stiffness [1].

The analysis of simple sandwich structures may be achieved by analytical methods, by adapting the classical tools of structural analysis on anisotropic elastic structure face elements. For more complex structures, such as more general boundary conditions or loading, numerical methods such as Finite Element Method, Boundary Element Method, etc. are used [2-5].

The use of assumptions is necessary to mathematical modeling of laminated composites. These include an elastic behavior of fibers and matrices, a perfect bonding between fibers and matrices, low variation of the mechanical characteristics of the individual fibers, uniform fiber diameters, their regular arrangement in the matrix, etc.

Taking into account the different size scales of mechanical modelling of structure elements composed of fiber reinforced composites, the micro, macro and structural modeling levels must be considered [6-10].

2. First-order shear deformation theory (FSDT)

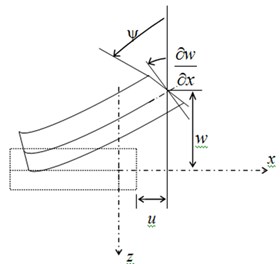
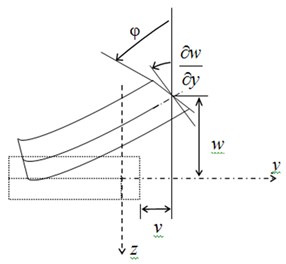
FSDT considers that transverse normal do not remain perpendicular to the midsurface after deformation. This theory is used for thicker plates or sandwiches taking into account the Reissner kinematics (Fig. 1).

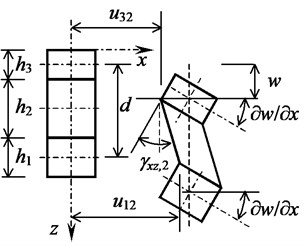
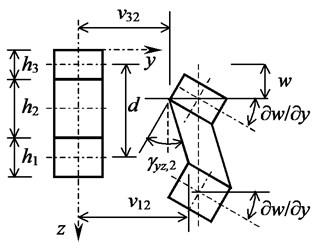
Transverse shear stresses are added to the state of plane stress for this reason. Shear deformations are written following the Fig. 2:

1

γ_{x z 2} = (\frac{u_{12} - u_{32}}{h_{2}} + \frac{\partial w}{\partial x}) = (\frac{u_{1} - u_{3}}{h_{2}} + \frac{d}{h_{2}} \frac{\partial w}{\partial x}),

γ_{y z 2} = (\frac{v_{12} - v_{32}}{h_{2}} + \frac{\partial w}{\partial y}) = (\frac{v_{1} - v_{3}}{h_{2}} + \frac{d}{h_{2}} \frac{\partial w}{\partial y}),

where $d$ is midplane distance of sandwich faces:

2

d = h_{2} + \frac{h_{1} + h_{3}}{2} .

Fig. 1Reissner kinematics

a)

b)

Fig. 2Geometry of shear deformation

a)

b)

Internal forces are expressed by terms:

3

N = \int_{- (\frac{1}{2} h^{(2)} + h^{(1)})}^{- \frac{1}{2} h^{(2)}} σ d z + \int_{\frac{1}{2} h^{(2)}}^{\frac{1}{2} h^{(2)} + h^{(3)}} σ d z,

M = \int_{- (\frac{1}{2} h^{(2)} + h^{(1)})}^{- \frac{1}{2} h^{(2)}} σ z d z + \int_{\frac{1}{2} h^{(2)}}^{\frac{1}{2} h^{(2)} + h^{(3)}} σ z d z,

V = \int_{- \frac{1}{2} h^{(2)}}^{\frac{1}{2} h^{(2)}} τ d z .

The constitutive equations for a sandwich are in the form:

4

(\begin{matrix} N \\ M \\ V \end{matrix}) = (\begin{matrix} A & B & 0 \\ C & D & 0 \\ 0 & 0 & A^{s} \end{matrix}) (\begin{matrix} ε_{m}^{0} \\ κ \\ γ \end{matrix}),

with stiffness coefficients:

5

A_{i j} = {A_{i j}}^{(1)} + {A_{i j}}^{(3)}, B_{i j} = \frac{1}{2} h^{(2)} ({A_{i j}}^{(3)} - {A_{i j}}^{(1)}), C_{i j} = {C_{i j}}^{(1)} + {C_{i j}}^{(3)},

D_{i j} = \frac{1}{2} h^{(2)} ({C_{i j}}^{(3)} - {C_{i j}}^{(1)}), A_{i j}^{s} = E_{i j}^{s} h^{(2)}, i, j = 4,5,

where $A_{i j}$ , $D_{i j}$ are coefficients of extension and bending stiffness matrix, $B_{i j}$ , $C_{i j}$ are coefficients of extension-bending coupling stiffness matrix, $E_{i j}^{s}$ are the transverse shear moduli of the core.

3. Free vibrations of sandwich plates

The equations to determine the natural frequencies of the symmetric sandwich panel are used [1]:

6

D_{11} \frac{\partial^{2} Φ_{x}}{\partial x^{2}} + D_{66} \frac{\partial^{2} Φ_{x}}{\partial y^{2}} + (D_{12} + D_{66}) \frac{\partial^{2} Φ_{y}}{\partial x \partial y} - k^{s} A_{55} (Φ_{x} + \frac{\partial w_{0}}{\partial x}) - I_{2} \frac{\partial^{2} Φ_{x}}{\partial t^{2}} = 0,

(D_{12} + D_{66}) \frac{\partial^{2} Φ_{x}}{\partial x \partial y} + D_{66} \frac{\partial^{2} Φ_{y}}{\partial x^{2}} + D_{22} \frac{\partial^{2} Φ_{y}}{\partial y^{2}} - k^{s} A_{44} (Φ_{y} + \frac{\partial w_{0}}{\partial y}) - I_{2} \frac{\partial^{2} Φ_{y}}{\partial t^{2}} = 0,

k^{s} A_{55} (\frac{\partial Φ_{x}}{\partial x} + \frac{\partial^{2} w}{\partial x^{2}}) + k^{s} A_{44} (\frac{\partial Φ_{y}}{\partial y} + \frac{\partial^{2} w_{0}}{\partial y^{2}}) - ρ_{m} h \frac{\partial^{2} w_{0}}{\partial t^{2}} = 0,

where $k^{s}$ is the transverse shear deformation factor given by value 5/6:

7

ρ_{m} = \frac{1}{h} \sum_{k = 1}^{N} ρ_{k} (z^{(k)} - z^{(k - 1)}), I = \frac{ρ_{m} h^{3}}{12} \frac{1}{3} \sum_{k = 1}^{N} ρ_{k} (z^{(k)})^{3} - (z^{(k - 1)})^{3},

where $ρ_{k}$ is the mass density of the $k$ th layer.

For the simply supported plate let:

8

w_{0} (x, y, t) = w_{0}^{°} e^{i ω_{m n} t}, Φ_{x} (x, y, t) = Φ_{x}^{°} e^{i ω_{m n} t}, Φ_{y} (x, y, t) = Φ_{y}^{°} e^{i ω_{m n} t},

where $m$ , $n$ – are integers only, $ω_{m n}$ – is natural angular velocity.

Ultimate length of sandwich panel depends on the ultimate frequency $f_{0, l i m}^{}$ of dynamic loading affected to the structures:

9

L_{0, l i m} = \sqrt{\frac{π m^{2} (\sqrt{k_{s}^{2} A_{_{55}}^{2} D_{11} h ρ_{m} + π^{2} D_{11} h_{_{}}^{2} ρ_{_{m}}^{2} f_{0, l i m}^{2}} - π D_{11} h ρ_{m} f_{0, l i m}^{})}{2 k_{s}^{} A_{_{55}}^{} h_{} ρ_{m} f_{0, l i m}^{}}} .

4. Numerical solution of sandwich panels

For the numerical solution, the simply supported panel with laminate facings was used. Panel length is 3250, 4250, 5250, 6250, 7100 mm, nominal width is 1000 mm. The thickness of the panel is 40, 80 and 120 mm. The thickness of laminate facings is 1 mm, composed of eight layers of symmetric [0/±45/90]_s, [0/90]_2s and [0/0]_2s laminates, respectively. The thickness of each laminate layer is 0.125 mm. Carbon fibers in epoxy matrix were considered [11], with the following characteristics: $E_{f} =$ 230 GPa; $E_{m} =$ 3 GPa; $ν_{f} =$ 0.3; $ν_{m} =$ 0.3; $ξ =$ 0.6; $ρ_{c} =$ 1508 kg/m³. Sandwich core, consisting of PUR foam, has material constants: $E_{P U R} =$ 25 MPa; $ν_{P U R} =$ 0.3; $ρ_{P U R} =$ 100 kg/m³.

Firstly, it has been done the modal analysis of the sandwich panels with a thickness of 40, 80 and , composed of eight layers of symmetric [0/±45/90]_s, [0/90]_2s and zero angles [0/0]_2s laminates as sandwich outer layers for 3250 mm panel length.

Table 1 shows the first natural frequency depending on the variation of fiber reinforced angle of the laminate facings and the core thickness of the sandwich panel. The natural frequencies depend on the rotation of individual layers to the global coordinate system, while the lowest value of first natural frequency was obtained for the sandwich panel with [0/45/-45/90]_s laminate faces and panel thickness 40 mm. Dependence of the natural frequencies from its natural mode shape of vibration by various faces is shown in the Fig. 3.

Table 1First natural frequencies f [Hz] of sandwich panels with length L= 3250 mm

Natural mode shape	Laminate [0/90]_2s			Laminate [0/±45/90]_s			Laminate [0/0]_2s
	Thickness [mm]			Thickness [mm]			Thickness [mm]
	40	80	120	40	80	120	40	80	120
1	13.7	21.8	27.7	11.9	18.5	23.6	18.5	29.2	36.7

Secondly, the modal analysis for various lengths of the sandwich panel with [0/45/-45/90]_s laminate faces was made to find the limit length of the panel, which is sensitive to dynamic wind load with $f_{0, l i m} =$ 5 Hz. The limit length of sandwich panels with [0/45/-45/90]_s laminate faces was found for various thicknesses of the sandwich. For sandwich panel 40, 80 and 120 mm thick, the limit length is 5.0 m, 6.25 m and 7.1 m, respectively. These types of sandwich panels are not sensitive to dynamic wind load under calculated limit lengths (Fig. 4).

Fig. 3Natural frequencies [Hz] of the first ten natural mode shapes of sandwich panels with 80 mm thickness

Fig. 4First natural frequencies [Hz] of sandwich panels with symmetric [0/±45/90]s laminate facings versus sandwich length

5. Conclusions

The mechanical properties of sandwich panels with laminate faces were investigated. Computational program MATLAB was used to calculate the effective material properties of laminate faces [12, 13]. The type of faces of a sandwich panel and the core thickness affect its natural frequencies. The first natural frequency of investigated laminate panels with the length $L =$ 3250 mm is up to $f_{0, l i m} =$ 5 Hz (Table 1), therefore the panels are not sensitive to the dynamic wind load. The sandwich panels with [0/45/-45/90]_s laminate faces and 40, 80 and 120 mm thick are not sensitive to dynamic wind load under their ultimate length 5.05 m, 6.25 and 7.1 m, respectively (Fig. 4).

References

Altenbach H., Altenbach J., Kissing W. Mechanics of Composite Structural Elements. Springer – Verlag, Berlin, 2004.

Publisher
Luciano R., Barbero E. J. Formulas for the stiffness of composites with periodic microstructure. Journal of Solids Structures, Vol. 31, Issue 21, 1994, p. 2933-2944.

Publisher
Reddy J. N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis. Second Edition, CRC Press, Florida, 2004.

Publisher
Carrera E., Pagani A., Valvano S. Multilayered plate elements accounting for refined theories and node-dependent kinematics. Compos Part B, Vol. 114, 2017, p. 189-210.

Publisher
Murčinková Z., Novák P., Kompiš V., Žmindák M. Homogenization of the finite-length fibre composite materials by boundary meshless type method. Archive of Applied Mechanics, Vol. 88, Issue 5, 2018, p. 789-804.

Publisher
Vorel J., Urbanová S., Grippon E., Jandejsek I., Maršálková M., Šejnoha M. Multi-scale modeling of textile reinforced ceramic composites. Ceramic Engineering and Science Proceedings, Vol. 34, Issue 10, 2014, p. 233-245.

Publisher
Sladek J., Novak P., Bishay P. L., Sladek V. Effective properties of cement-based porous piezoelectric ceramic composites. Construction and Building Materials, Vol. 190, 2018, p. 1208-1214.

Publisher
Brischetto S. Convergence analysis of the exponential matrix method for the solution of 3D equilibrium equations for free vibration analysis of plates and shells. Compos Part B, Vol. 98, 2016, p. 453-71.

Publisher
Yhang L. W., Xiao L. N. Mechanical behavior of laminated CNT-reinforced composite skew plates subjected to dynamic loading. Compos Part B, Vol. 122, 2017, p. 219-230.

Publisher
Chandrashekara C. V., Suswaram P. E., Dharani J., Agarwal H., Raj Arjun S. I. Formulation of effective stiffness for predicting natural frequency of cracked beams. Vibroengineering Procedia, Vol. 19, 2018, p. 135-140.

Publisher
Piovar S., Kormanikova E. Statical and dynamical analysis of composite sandwich plates. Bulletin of the Transilvania University of Braşov Series I: Engineering Sciences, Vol. 4(53), Issues 1, 2011, p. 177-184.

Search CrossRef
Kormaníková E., Kotrasová K. Resonant frequencies and mode shapes of rectangular sandwich plate. Chemicke listy, Vol. 105, Issue 16, 2011, p. 535-538.

Search CrossRef
Chen W., Meng Q., Hao H., Ciu J., Shi Y. Quasi-static and dynamic tensile properties of fiberglass/epoxy laminate sheet. Construction and Building Materials, Vol. 143, 2017, p. 247-259.

Publisher

Cited by

FEA of stress-strain state and vibrations of a three-layer plate

Iaroslav Lavrenko | Maksym Sushchenko

(2024)

Multi-objective optimization of composite sandwich panels using lamination parameters and spectral Chebyshev method

Farzad Seyyedrahmani | Peiman Khandar Shahabad | Gokhan Serhat | Bekir Bediz | Ipek Basdogan

(2022)

Passive Multi-Layer Composite Damper of Flat Belt Tensioner Idler

Zuzana Murčinková | Jozef Živčák | Jozef Zajac | Pavel Adamčík

(2021)

About this article

Received

15 March 2019

Accepted

22 March 2019

Published

25 April 2019

SUBJECTS

Modal analysis and applications

DOI

https://doi.org/10.21595/vp.2019.20658

Keywords

sandwich panel

mode shape

natural frequencies

limit length

Acknowledgements

This work was supported by the Scientific Grant Agency of the Ministry of Education of Slovak Republic and the Slovak Academy of Sciences under Projects VEGA 1/0374/19 and 1/0078/16.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2022 05 16

Influence determination of damage to mechanical structure based on modal analysis and modal assurance criterion

Mehran Khan, Swarup Mahato, Darius Eidukynas, Tomas Vaitkunas

Research article

2019 02 15

Sensitivity analyses of resonant frequencies and modal strain energy of damaged beams by perturbation method

G. Chen, P. P. Gong, P. Liang

Research article

2018 09 24

Formulation of effective stiffness for predicting natural frequency of cracked beams

C. V. Chandrashekara, Pavan Suswaram, Dharani J., Himanshu Agarwal, Raj Arjun S. I.

Research article

2018 08 15

A unified Gram-Schmidt-Ritz formulation for vibration and active flutter control analysis of honeycomb sandwich plate with general elastic support

Huagang Lin, Dengqing Cao

E. Kormanikova, “Modal analysis of sandwich panel with composite laminated faces,” Vibroengineering PROCEDIA, Vol. 23, pp. 105–109, Apr. 2019, https://doi.org/10.21595/vp.2019.20658

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2019.20658
UR  - https://doi.org/10.21595/vp.2019.20658
TI  - Modal analysis of sandwich panel with composite laminated faces
T2  - Vibroengineering PROCEDIA
AU  - Kormanikova, Eva
PY  - 2019
DA  - 2019/04/25
PB  - JVE International Ltd.
SP  - 105-109
VL  - 23
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Kormanikova_2019,
	doi = {10.21595/vp.2019.20658},
	url = {https://doi.org/10.21595/vp.2019.20658},
	year = 2019,
	month = {apr},
	publisher = {{JVE} International Ltd.},
	volume = {23},
	pages = {105--109},
	author = {Eva Kormanikova},
	title = {Modal analysis of sandwich panel with composite laminated faces},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]E. Kormanikova, “Modal analysis of sandwich panel with composite laminated faces,” Vibroengineering PROCEDIA, vol. 23, pp. 105–109, Apr. 2019, doi: 10.21595/vp.2019.20658.

Copy IEEE

Copied to clipboard!

Kormanikova, Eva. “Modal Analysis of Sandwich Panel with Composite Laminated Faces.” Vibroengineering PROCEDIA 23 (April 25, 2019): 105–9. https://doi.org/10.21595/vp.2019.20658.

Copy Chicago

Copied to clipboard!

Modal analysis of sandwich panel with composite laminated faces

Abstract

Highlights

1. Introduction

2. First-order shear deformation theory (FSDT)

3. Free vibrations of sandwich plates

4. Numerical solution of sandwich panels

5. Conclusions

References

Cited by

About this article

Related Articles