Dynamic characterization and modeling of steel foam sandwich structure

1. Introduction

Presently, steel foams are defectively characterized, nevertheless, these materials have been developed instantly and are using as a new porous metal since the last decades [1]. Besides, they have individual physical attributes and mechanical characteristics, suchlike high specific stiffness and strength, perfect plastic energy absorption at a low weight, and superior corrosion resistance together with high damping [2]. However, fabrications based on these lightweight materials are almost new and unknown; though in the past few years, these metallic foams provide notable potential applications in various industries. Furthermore, they are non-toxic materials, recyclable, have a resistance potential to the shock and blast more than those solid structures with the equivalent mass [3-5].

The inspiration for this research project was based on the theory that the steel foams are an excellent class of composite materials that can be employed as the ultra-light stiffeners against buckling, which can also mitigate vibrations in aerospace and civil applications, and some infrastructures such as wind turbine towers and steel bridges and armors either military or civil uses [2-6]. The metallic foams structural properties are defined according to the relative density, cell topology (Close or Open Cell) and its size, and anisotropy.

Three main manufacturing methods for making metallic foams are 1. Hollow spheres (it has been employed efficiently in commercial production and the most appropriate method for this research work), 2. Powder metallurgy (it is still employing effectively to develop structural steel foam models and prototypes), and 3. Lotus (it has a high capability for casting processes continuously with low cost).

There is numerous studying of the damping coefficients in particular for aluminum foams, nevertheless, the large variability of the results due to the material characterization and various approaches exist. This work proposes to define the dynamic properties of the steel foam cantilever specimens with random noise test. The purpose is to examine the damping characteristics of the 2-phase material over a spectrum of frequencies and evaluating the damping ratio increase.

2. Finite element model

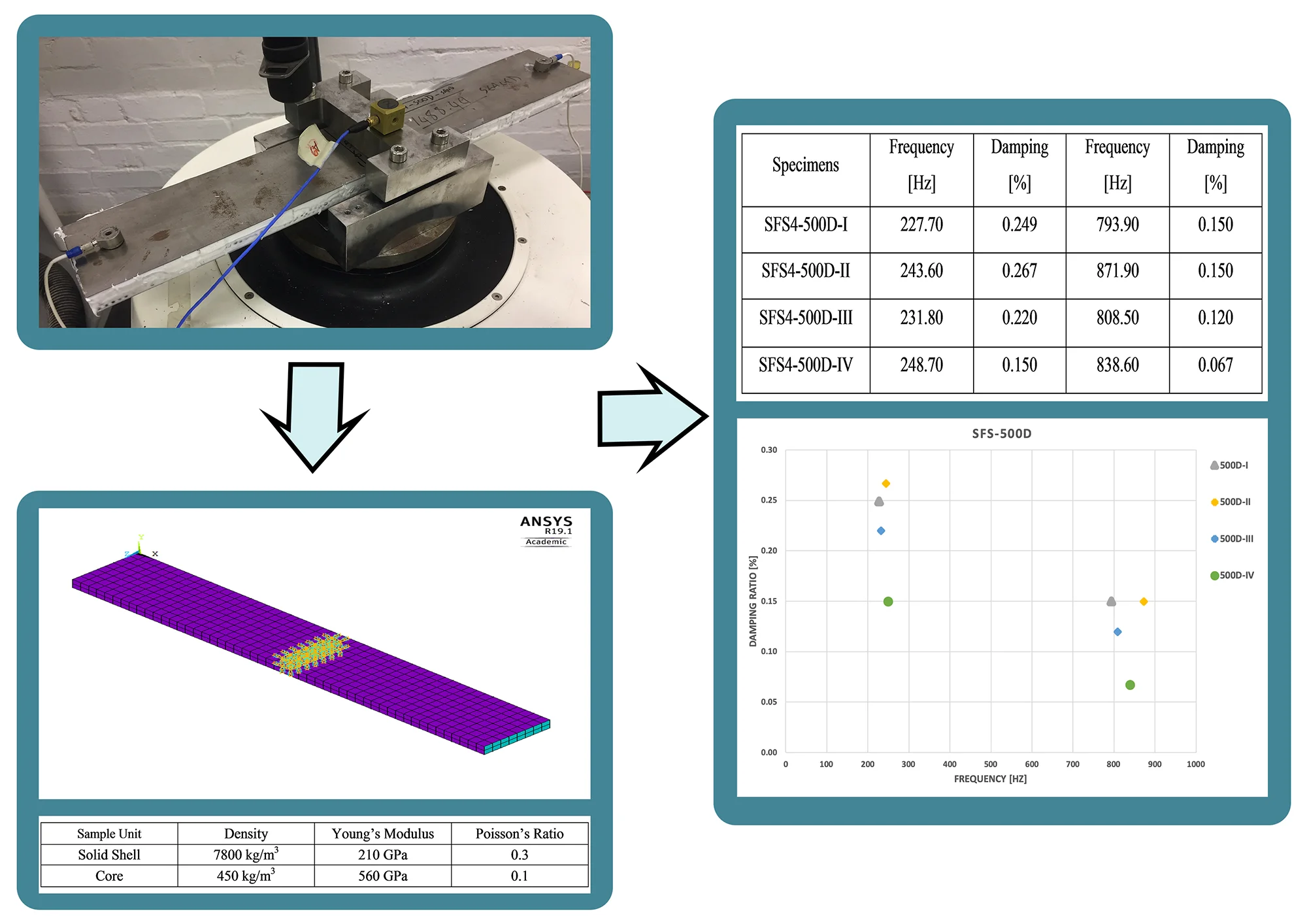
For the aim of reproducing of the damping behavior of steel foams in finite element analysis, the model is built in APDL ANSYS V19.1. The model (Fig. 1) contains the geometry of sandwich composite 500D with 30 mm length of clamping section and 80 mm of the side length, moreover, the thickness of face-sheet in this model is negligible. The constraint has been fixed the DOF on below and top of the clamping part.

Fig. 1Sandwich specimen (500D) finite element model by ANSYS 19.1

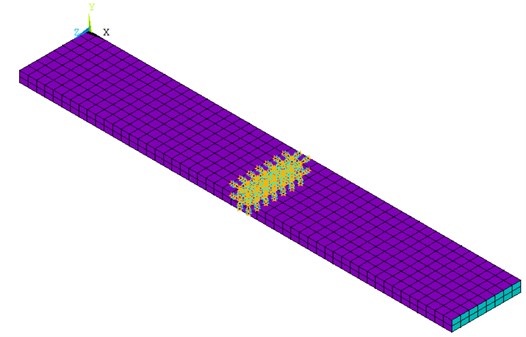
The FEM analysis by using ANSYS APDL has achieved with two major analysis steps: extraction of frequency by employing dynamic time-dependent model analysis was the first step, and the harmonic analysis applied by using the random noise test was the second run [6]. The mechanical material features of the designated sample are shown in Table 1. It has been considered an undamped model for the modal analysis, though, for the harmonic analysis; 5 % material damping for each mode is implemented to set with experimental values. The mesh of the specimen is composed of 1900 Elements and 1404 nodes in the purpose of having deformation control.

Giving the fact that the metallic foams materials are greatly engineered, using finite element techniques to improve their material properties and monitor their behavior is an efficient and cost-effective procedure to understand how these materials are behaving.

3. Experimental setup

The sandwich has been employed for the investigation was made by Hollomet GmbH with hollow sphere manufacturing method (Fig. 2) and including thermosetting epoxy Araldite AT1-1 in order to form the sandwich core configuration surrounded by two mild steel faceplate DC01 [7].

On the basis of increasing the demand interest to use the lightweight structures in the advanced industries and fast operation, static analysis alone cannot be sufficient and adequate; furthermore, the vibrational examination is needed. To produce vibration and detect the dynamic properties of the specimens an electromagnetic vibration exciter (shaker) is employed (Fig. 3).

Fig. 2Hollomet specimen

Fig. 3Electrodynamics shaker V400HG/DSA4 of data-physics

The closed-loop control of the shaker was provided by a Signal-Star Vibration Controller and the corresponding control software. The Polytec OFV-505 laser vibrometer and PCB piezoelectric have been employed to measure the outputs on the tips of each sample and the shaker feedback signal respectively (Fig. 2). Moreover, 20 N.m torque has been applied to clamp the specimen to the shaker table and reduce the damping friction and the laser vibrometer spot was centrally positioned in the cantilevers.

For the 500 mm samples, the random noise testing with 30 to 2000 Hz bandwidth has been chosen to eliminate the low-level frequencies (under 30 Hz) from the input to decrease the shaker displacements. No relevant modes are present at those low frequencies, so it was an appropriate assumption. For all the tests the acquisition setup has been the same, a National Instrument data acquisition NI-9234 module has been used and the signals were acquired using standard LabView software at a sampling frequency of 10240 Hz.

4. Analysis

FRF model has been analyzed for different samples together with the varying frequencies range (0-2000 Hz). As the results obtained by FEM optimization, damping ratio has been found by random noise experimental results comparison. The results based on the final damping ratios for each sample are listed in Table 2.

The dispersion of the damping ratio along with the increasing frequency for different specimens has been presented in Fig. 4. The standard deviations are 0.051 and 0.039 respectively for the first and second mode. Moreover, the mean value of damping ratio for the first mode is 0.22 and for the second mode is 0.12.

5. Discussion

The experimental outcomes for the double cantilever specimens (500D) designate sufficient results by considering just 3-5 % difference for the first mode shape and with 10 % variation for second mode shapes with the identical test. The method illustrates an apparent decay in damping ratios at increasing frequencies. When examining the 2-phase cores (i.e. presence of sand into the core), the random noise test has been shown a slight differences between the specimens.

Fig. 4Damping ratio [%] vs. frequency [Hz] for all 500D samples

6. Conclusions

This research work was a short examination to evaluate the lightweight metallic foam structure to perform like a passive damper. In order to achieve that, random noise experimental tests were performed to investigate the appropriate steel foam structure in a double-phase core. Besides, the output frequency result of ’Random Noise Test’ compared with the analytical model made by ANSYS. The damping ratios for different specimens have been calculated and for the first resonant frequency, the ratio is increasing regarding having the two-phase sandwich core for the samples.