Effect of mounting and fluid parameters on dynamic damping characteristics of a hydraulic damper

2.1. Mathematical modelling

A mathematical model describing DDC of a CRH380 high-speed train hydraulic yaw damper, as shown in Fig. 1, is built. The transient damping force of the hydraulic damper during extension and compression can be respectively formulated by:

where $m_1$ is mass of the moving part, $x_2$ is actual displacement input, $c_1$, $f_1$ are respectively damping coefficient and friction coefficient of the rod, $d$, $D$ are respectively diameters of the rod and the piston, $p$ is pressure of the inner tube.

Fig. 1A hydraulic yaw damper used in the Chinese CRH 380 high-speed train

The flow continuity equation of the damper during extension and compression can be respectively formulated by:

where $Q_1$, $Q_v$ are total flow loss and discharged flow from the complete-valve-system. In formulating $Q_1$, the total flow loss model introduced in [11] can be used.

In addition, because a four-stage complete-valve-system [11, 12] is used in the yaw damper, so the pressure-flow characteristics of the complete-valve-system would be formulated by:

where $d_1$, $d_4$ are respectively diameters of constant orifices in the valve 1 and 4, $C_d$ is discharge coefficient, $\rho$ is oil density, $v_4$ is the fourth typical speed, $k_2$, $k_3$, $k_4$ are spring stiff nesses of the valve 2, 3 and 4, $p$, $p_b$, $p_1$~$p_4$ are pressures of the inner tube, back pressure in the outer tube and set pressures of the valve 1-4, ${\delta }_2$~${\delta }_4$ are respectively opening heights of the valve 2-4, $E_1$~$E_4$ are respectively set pressure deviations of the valve 1-4.

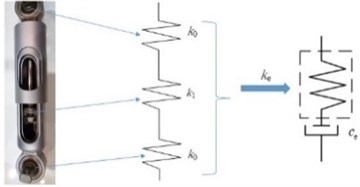
As illustrated by Fig. 2, equivalent stiffness $K_e$ of the hydraulic damper comprises of the rubber attachment stiffness $k_0$ and the oil stiffness $k_1$, so $K_e$ is formulated by:

Fig. 2Equivalent stiffness model of hydraulic damper

The oil stiffness $k_1$ can be described by:

where $E$, $E_0$ are respective dynamic elasticity modulus and elasticity modulus at initial conditions of the oil, $p$, $p_0$ are respectively working pressure of the damper and standard atmospheric pressure, $\epsilon$ is entrapped air ratio in the damper fluid, $s$ is the working pressure action area, $V$ is volume of the pressure chamber of the damper, thus, it can be formulated by:

for the extension stroke of the damper, and:

for the compression stroke, where $x$ is the displacement of the damper, $H$ and $h$ are heights of inner tube and piston.

Asa result, the above equations are coupled to obtain a full-parametric model, which describes the DDC of the hydraulic damper.

2.2. Simulation and experimental validation

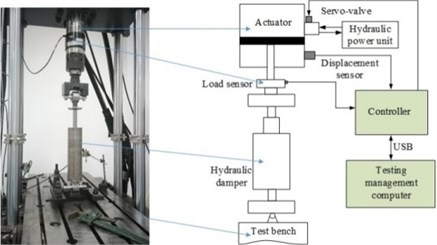
DDC of the hydraulic damper is simulated in MATLAB environment by means of the established full-parametric model, bench testing of the hydraulic damper, as illustrated in Fig. 3, is also conducted by a MTS test stand with hydro-servo excitation system [12], thus, the built full-parametric DDC model of the hydraulic damper is validated [12], it is appropriate for damper parameter influence analysis.

Fig. 3Testing the damping characteristics in a MTS test rig

3.1. Effect of attachment stiffness on DDC

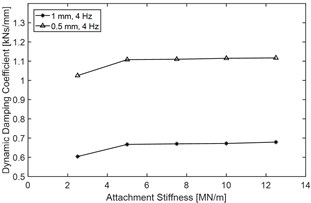
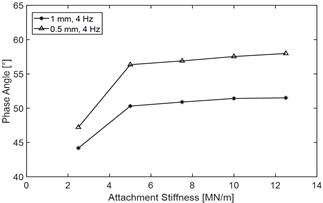
Parameter influence on DDC of the hydraulic yaw damper is simulated in MATLAB environment by means of the built mathematical model. Fig. 4 illustrates the influence of rubber attachment stiffness on main DDC indices.

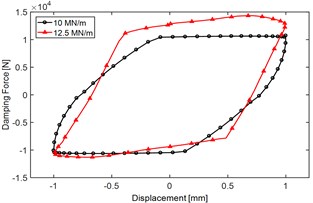
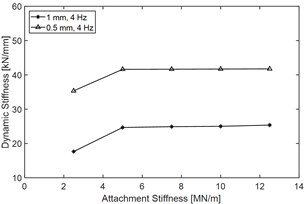
Fig. 4Effect of rubber attachment stiffness k0 on main DDC indices of the yaw damper: a) force-displacement performance when with different rubber attachment stiffness, test condition: excitation frequency 2 Hz and amplitude 1 mm, b) dynamic stiffness vs. k0, c) dynamic damping coefficient vs. k0 and d) phase angle vs. k0

a)

b)

c)

d)

Fig. 4(a) demonstrates that variations of rubber attachment stiffness would cause obvious change of Force-displacement characteristics. Fig. 4(b), (c) and (d) show that when attachment stiffness is less than 7.5 MN/mm, with the increasing of $k_0$, all of the dynamic indices will increase obviously, however, when the attachment stiffness exceeds 7.5 MN/mm, with the increasing of $k_0$, the dynamic stiffness and the dynamic damping coefficient both remain level, the phase angle will increase slightly.

Table 1 shows the main DDC indices and its change rate when $k_0$increases from 2.5 MN/mm to 10 MN/mm, and it demonstrates that increasing of attachment stiffness would increase almost all of the main dynamic damping indices regardless of the excitation amplitude, for example, when the excitation amplitude is 1 mm, and $k_0$ increases from 2.5 MN/mm to 10 MN/mm, the dynamic stiffness would increase by 41.7 %, the dynamic damping coefficient would increase by 11.3 %, and the phase angle would increase by 16.4 %.

3.2. Effect of air entrapment in the fluid on DDC

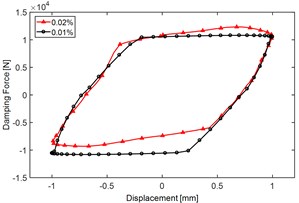
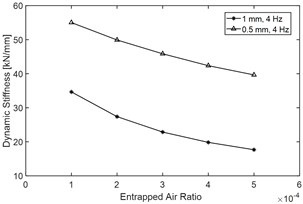
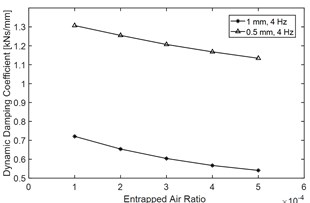
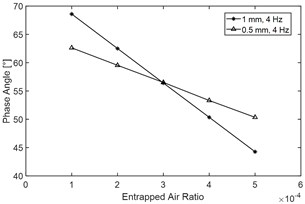
Fig. 5 demonstrates the effect of entrapped air ratio $\epsilon$ on main indices of the DDC. Fig. 5(a) illustrates that variation of $\epsilon$ would lead to obvious change of Force-displacement characteristics, Fig. 5(b), (c) and (d) also show that with the increasing of $\epsilon$, all of the DDC indices will decrease apparently, especially the phase angle will drop obviously, thus, it indicates that air entrapment of the fluid would apparently decrease the elasticity modulus of the fluid and weaken the dynamic performance of the damper.

Table 2 quantification ally compares the main DDC indices and its change rate when entrapped air ratio $\epsilon$ increases from 0.01 % to 0.04 %, and it demonstrates that increasing of $\epsilon$ would decrease almost all the main dynamic damping indices regardless of the excitation amplitude, for example, when the excitation amplitude is 1 mm, and ɛ increases from 0.01 % to 0.04 %, the dynamic stiffness would drop by 42.8 %, the dynamic damping coefficient would decrease by 21.4 %, and the phase angle would drop by 26.6 %.

Fig. 5Effect of entrapped air ratio ε on main DDC indices of the hydraulic yaw damper: a) an illustration of force-displacement characteristics when with different entrapped air ratio, test condition: excitation frequency 2 Hz and amplitude 1 mm, b) dynamic stiffness vs. ε, c) dynamic damping coefficient vs. ε and d) phase angle vs. ε

a)

b)

c)

d)