Clustering of ECG segments for patients before sudden cardiac death based on Lagrange descriptors

1.1. Data description

In this paper we use Sudden Cardiac Death Database available at PhysioNet [10]. The database contains 23 complete Holter recordings. Each recording comprises 2 time series – two lead ECG. For short description of the data used refer to Table 1.

We have analyzed each data file of the database but provide results here for the first entry i.e. file “30m.mat”.

1.2. Methodology

Consider ECG signal $X_t$, $t=1,2,\dots ,N$. Since the aim here is to investigate the dynamics of extracted features in different segments of ECG, the signal is divided into 5 data sets of equal length: $x_t^{\left(q\right)}=X_{\left(q-1\right)\bullet ⌊N/5⌋+t}^{}$, $t=1,2,\dots ,⌊N/5⌋$, $q=1,2,\dots ,5$. Each segment is investigated separately using the same methodology.

Datasets $x_t^{\left(q\right)}$ are further divided into a number of non-overlapping vectors $y_i^{\left(q,c\right)}\text{,}$$c=⌊⌊N/5⌋/256⌋$, $i=1,2,\dots ,256$. Now, time embedding is performed for each vector and collection of triples of ECG values are computed: ${\left(u_i,v_i,w_i\right)}_{{\tau }_1,{\tau }_2}:=\left(y_i^{\left(q,c\right)},y_{i+{\tau }_1}^{\left(q,c\right)},y_{i+{\tau }_1+{\tau }_2}^{\left(q,c\right)}\right)$, ${\tau }_1,{\tau }_2=1,2,\dots ,48$, $i=1,2,\dots ,166$. This is in fact a standard non-uniform time series embedding approach. Thus, the triples obtained could be treated as points of a trajectory in 3D space. Lengths $L\left({\tau }_1,{\tau }_2\right)$ of the vectors ${\left(u_i,v_i,w_i\right)}_{{\tau }_1,{\tau }_2}$ are the simplest LD estimates and are computed by Eq. (1).

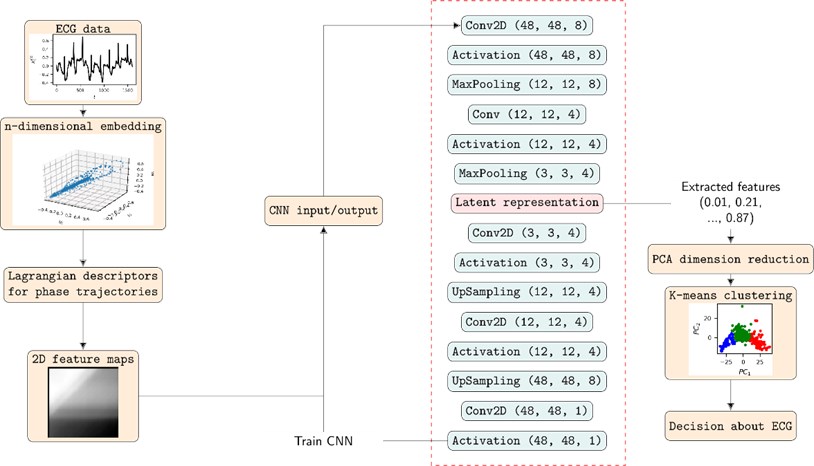
LD estimates are then used for 2D feature computation. We place a dot of grayscale intensity $L\left({\tau }_1,{\tau }_2\right)$ in the two-dimensional plane at coordinates $\left({\tau }_1,{\tau }_2\right)$. After considering ${\tau }_1,{\tau }_2=1,2,\dots ,48$ two-dimensional features are obtained for ECG segments $x_t^{\left(q\right)}$. Clustering of the features is a rather straightforward task. So CNN is employed for extracting second level features – latent vectors. These are later fed to dimensionality reduction by PCA (leaving only 2 components, just for the visualization purposes) and clustered by K-means. Fig. 1 shows full diagram of the methodology proposed for clustering of ECG segments.

Fig. 1Full diagram of the methodology presented in this paper together with the structure of CNN for extracting latent vectors (second level features) from 2D features of ECG

1.3. Numerical experiments

At first 2D feature maps must be computed. Actually, this step of preprocessing implies a very big number of numerical experiments to be carried out. We have used two-dimensional time embedding together with the simplest LD estimate as mentioned before. One can try different dimensions as well as different LD estimates but that would only lead to optimal feature extraction technique and not tell more details about the methodology itself.

First three 2D feature maps for the first data file and the measurements of the first lead are shown in Fig. 2.

Fig. 2A subset of 2D features of ECG segments before sudden cardiac death for “30m.mat” data file

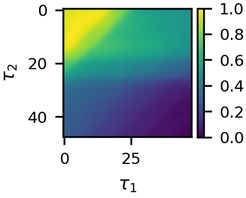
a)

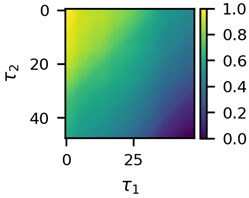
b)

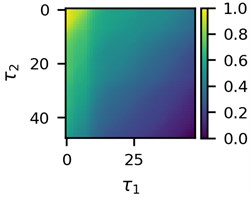
c)

Visual differences in Fig. 2 implies that clustering of such mages would be a logical step to try to find different clusters for the beginning of the recordings and for the end of the recordings. This is the ultimate goal of the research presented here.

Next, optimal CNN must be trained on the obtained 2D feature maps and latent vectors computed. It should be noted that we linearly transform the values in the maps to the interval $\left[0;1\right]$ before applying CNN. For training of CNN we have tested filter sizes 4 and 8, 4 and 8 for number of convolutional filters in the first layer of the network, 2 and 4 for number of filters in the second layer as well as 2 and 4 for parameters in downsampling (MaxPooling) layers. We have used python with keras for training of CNN. Computations took significant amount of time to complete. For that matter cuda hardware acceleration was employed. Training performance was measured by the mean squared error (MSE). Table 2 shows best CNN architectures for the first data file.

Table 2 shows that bigger filter sizes are preferred in terms of MSE. It could be also noted that MSE in validation set is always lower compared to the MSE in the training set. This ensures that there was no overfitting during the training process. Since there are no big differences between the MSEs for different optimal CNN architectures we fix parameters $n_{c1}=\text{8}$, $n_{c2}=\text{4}$, $n_{p1}=\text{2}$, $n_{p2}=\text{2}$ and 8 as the dimension of convolutional filters for the experiments presented in this paper.

The change in training performance of CNN is depicted in Fig. 3. Note that the plots of training performance for other data files are of almost identical shape.

Fig. 3Training performance of CNN

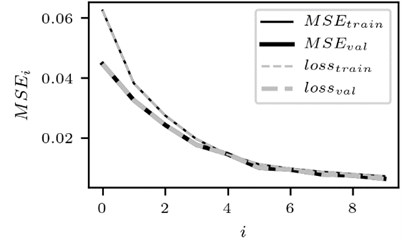
a) The case for the signal of the lead 1

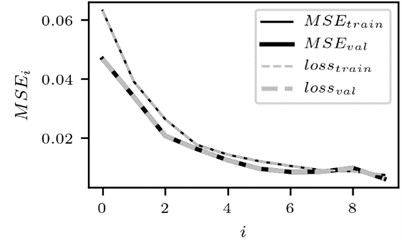
b) The case for lead 2

Optimal CNN network was employed and sets of latent vectors were computed for each segment of ECG. Clustering of the latent vectors for the measurements from the first lead from “30m.mat” data file is depicted in Fig. 4.

Fig. 4Clusters of latent vectors corresponding to different segments of ECG before sudden cardiac death (1st lead of the “30m.mat” data file). Colors depict different clusters and are not related in any manner between different parts a) – e)

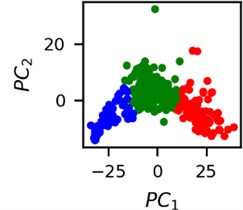
a)

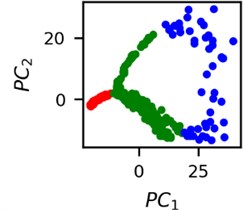
b)

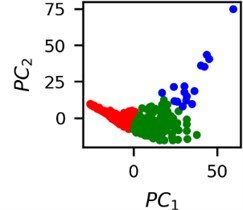
c)

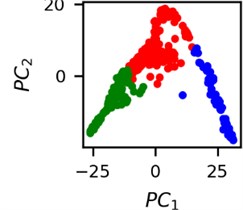
d)

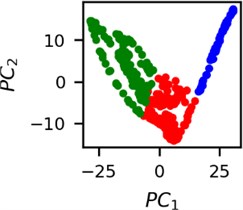
e)

It is known that 2 hours before sudden cardiac death is the time window in which an expert can spot unnatural and potentially risky ECG activity [1]. In Fig. 4 we clearly see that 5 segments during the last 25 minutes have visibly different clusters of latent space vectors. Same applies to the lead 2 (Fig. 5). Unfortunately, the data sets used do not have more measurements which could span more than 2 hours. That would be especially valuable for the validation if the methodology proposed actually signals something unusual before the SCD happens.

Note that shapes of clusters of the vectors of latent space in general have some similar areas between different segments of ECG and even between different data files. This suggests that the proposed methodology might not be completely random. Of course, bigger data sets are required to prove or disprove this.

Fig. 5Clusters of latent vectors corresponding to different segments of ECG before sudden cardiac death (2nd lead of the “30m.mat” data file). Colors depict different clusters and are not related in any manner between different parts a) – e)

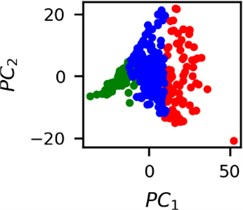
a)

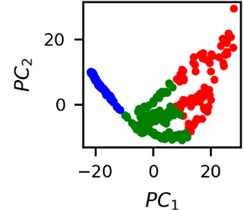
b)

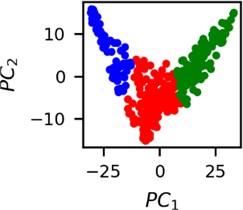
c)

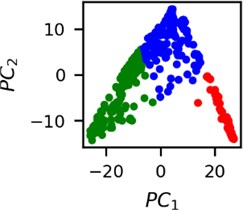
d)

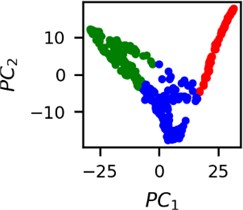
e)