Nonlinear free vibration analysis of levy plates using weak-form variational principle in polynomial displacement functions

Onodagu, P. D.; Okonkwo, V. O.; Aginam, C. H.

doi:10.21595/mme.2019.21212

Mathematical Models in Engineering

Browse Journal

Submit article

Published: 31 December 2019

Check for updates

Nonlinear free vibration analysis of levy plates using weak-form variational principle in polynomial displacement functions

P. D. Onodagu¹

V. O. Okonkwo²

C. H. Aginam³

^{1, 2, 3}Department of Civil Engineering, Nnamdi Azikiwe University, Awka, Anambra State, Nigeria

Corresponding Author:

P. D. Onodagu

Cite the article Download PDF

Downloads 1062

Abstract

This paper evaluates nonlinear free vibrations of Levy plates using Weak-Form variational principle in algebraic polynomial displacement functions. The energy functional of the plate problem was formulated using Weak-Form variational technique on the integral function of the Von Karman thin plate differential equations. The displacement functions were developed based on static deflection configurations of orthogonal beam network. The process of repeated direct integration on compatibility equation was used to determine the algebraic expressions for stress function. The amplitude of deflection which directly influences the geometric nonlinearity of the plate was determined using integration process on energy functional based on static equilibrium equations. The modal combination method was used to develop the stiffness and mass matrices respectively from the expressions of energy functional based on dynamic equilibrium equations. The numerical values of amplitudes of deflection at various aspect ratios were computed. Also, the first four nonlinear natural frequencies at various aspect ratios were numerically computed. The validation of the present study’s results using the results from previous work found in literature shows satisfactory convergence, with an absolute mean error of 0.186 %. Conclusively, the application of Weak-Form variational principle in polynomial displacement functions provides satisfactory approximation to nonlinear dynamic analysis of Levy plates.

1. Introduction

A levy plate in the context of this paper refers to any rectangular plate in which at least two opposite edge conditions are simply supported; and any of the two remaining edge conditions can either be clamped, simply supported or free. Engineering applications of levy plates are widely found in bridges, houses, marine structures, vehicular structures and airspace structures. In practice, almost all the rectangular plates engaged in the construction of these structures are classified as thin-walled structural components. Sequel to their thinness, the plates are often prone to large deformation in their engineering applications due to the influence of external disturbances. Consequently, the appropriate engineering analysis that is capable of simulating the actual response of thin rectangular plates to external disturbances must be the one formulated based on nonlinear mathematical model. However, the implication of using nonlinear mathematical model to determine the plate response is that the resulting nonlinear differential equations of equilibrium are likely going to impose complex mathematical challenges, and sometimes the closed-form solutions are absent. This problem is readily observed in the case of plates with mixed boundary conditions (majority of levy plates), which exhibit discontinuities in the edge supports [1].

For the fact that the resulting nonlinear differential equations from nonlinear method of analysis are tedious to tackle, approximation mathematical models have been developed to ameliorate the problem. Consequently, many of the investigators on large amplitude of vibrations of rectangular thin plates apply different approximation techniques to tackle the problem of nonlinear vibrations of thin rectangular plates.

1.1. Related works

Engineering analysis of thin rectangular plates based on large amplitude of vibrations has for decade now posed interesting and challenging research fields. A number of approximation techniques have been developed for the purposes of investigating into large amplitude of vibrations of thin rectangular plates. [2] used Herrmann equations of motion in Galerkin technique to study the effect of initially applied stress on the nonlinear vibrations of flat plate. Finite element methods were used by [3-5] to investigate into large amplitude of vibrations of rectangular plates. Analytical technique on dynamic analogue of Von Karman differential equations was employed by [6] to investigate the effect of initial geometric imperfections and in-plane boundary conditions on the large amplitude of vibrations of angle- and cross -ply rectangular thin plates. [7] used levy solutions to study the vibration behaviour of multi-span rectangular plates. A combination of static and dynamic method-problem solving was used by [8] to investigate geometrically nonlinear free vibration of square plates with various boundary conditions. Second order asymptotic method was employed by [9] to investigate the effect of geometric imperfections on the amplitude of nonlinear vibrations of thin rectangular plates that were parametrically excited. A multiple scale method was used by [10] to investigate the nonlinear vibration of rectangular plates. Mesh-free least squares-based finite difference method was used by [11] to investigate large amplitude of vibrations of arbitrarily shaped thin plates. [12] used first order finite element theory to study free vibration of composite plates. A combination of Hamilton principle and Galerkin method was used by [13] to investigate nonlinear dynamic response of a simply supported functionally graded rectangular plate under the time-dependent thermalmechanical loads. Also, [14] used finite strip formulation to study nonlinear free vibration of plates. Furthermore, [15] used analytical technique, numerical and experimental analysis to study vibration behaviour of laminated composite plates under thermo-mechanical loading. The Galerkin-Vlasov method was used by [16] to obtain solution of free harmonic vibration of simply supported Kirchhoff plate.

1.2. Statement of problem and objectives

The energy methods have been proven to be very powerful for solving structural problems, especially those ones subjected to large deformations and large amplitude of vibrations. In analytical energy approach, the commonest approximation techniques appearing in most technical literature are the Hamilton’s energy principle, the classical direct variational principle in Ritz method, and the residual energy method in Galerkin approach. Also, the most commonly used displacement functions are the trigonometric functions, either in the form of single or double Fourier series. There is need therefore, to explore other simple but accurate approximation techniques to be used in formulating energy functional for structural problems.

The primary objective of this study is to apply Weak-Form variational principle in formulating energy functional for nonlinear rectangular plate problem. The secondary objective is to develop and apply algebraic polynomial shape functions admissible to various levy plate boundary conditions.

2. Theoretical formulations

Fig. 1 shows a rectangular thin isotropic plate of levy type in which the edges $x =$ 0 and $x = a$ are parallel and simply supported.

The boundary conditions of the edges $y =$ 0 and $y = b$ are arbitrary; and each of them can either be clamped, simply supported or free. The plate is invariant in engineering properties of Young modulus $E$ and Poisson’s ratio $μ$ , and it has constant mass density $ρ$ . The plate lateral dimensions are defined by $a$ and $b$ as the length and width respectively.

Fig. 1A rectangular plate showing at least two edges parallel and simply supported

2.1. Formulation of energy functional

The Weak-form variational principle is used to formulate the energy functional of the plate problems. The plate is assumed to be thin; and it satisfies the integral function of Von Karman’s thin plate differential equations. The analogous Von Karman’s thin plate differential equations of motion are as expressed in Eqs. (1-2):

1

\nabla^{4} w = \frac{1}{D} [q + \frac{\partial^{2} F}{\partial y^{2}} \frac{\partial^{2} w}{\partial x^{2}} - 2 \frac{\partial^{2} F}{\partial x \partial y} \frac{\partial^{2} w}{\partial x \partial y} + \frac{\partial^{2} F}{\partial x^{2}} \frac{\partial^{2} w}{\partial y^{2}} - ρ t \ddot{w}],

2

\nabla^{4} F = E t [{(\frac{\partial^{2} w}{\partial x \partial y})}^{2} - \frac{\partial^{2} w}{\partial x^{2}} \frac{\partial^{2} w}{\partial y^{2}}],

where $E$ is Young modulus of plate materials; $w$ is displacement functions; $F$ is Airy’s stress functions; $t$ is plate thickness; $ρ$ is mass density of plate materials; $q$ is uniformly applied lateral load; $\ddot{w}$ is second derivative of $w$ with respect to time $T$ ; $D$ is flexural rigidity of the plate

Let $V (x, y)$ be defined as weighting function which is admissible to boundary conditions of the levy plates. Then the variational statement is applied on the integral functions of Eq. (1) as expressed in Eq. (3):

3

0 = \int_{0}^{a} \int_{0}^{b} V (x, y) [\frac{\partial^{4} w}{\partial x^{4}} + 2 \frac{\partial^{4} w}{\partial x^{2} \partial y^{2}} + \frac{\partial^{4} w}{\partial y^{4}} - \frac{1}{D} (q + \frac{\partial^{2} F}{\partial y^{2}} \frac{\partial^{2} w}{\partial x^{2}} - 2 \frac{\partial^{2} F}{\partial x \partial y} \frac{\partial^{2} w}{\partial x \partial y} + \frac{\partial^{2} F}{\partial x^{2}} \frac{\partial^{2} w}{\partial y^{2}} - ρ t \ddot{w})] d x d y,

where $D$ is defined as expressed in Eq. (4):

4

D = \frac{E t^{3}}{12 (1 - μ^{2})},

where $μ$ is Poisson’s ratio.

Let $K$ be the reciprocal of $D$ as given by Eq. (5):

5

K = \frac{1}{D} .

Integration by parts is exercised on Eq. (3) to trade differentiation from $w$ and $F$ to $V (x, y)$ , and after simplification yields the expressions as given in Eq. (6):

6

0 = \int_{0}^{a} \int_{0}^{b} [\frac{\partial^{2} V}{\partial x^{2}} \frac{\partial^{2} w}{\partial x^{2}} + 2 \frac{\partial^{2} V}{\partial x \partial y} \frac{\partial^{2} w}{\partial x \partial y} + \frac{\partial^{2} V}{\partial y^{2}} \frac{\partial^{2} w}{\partial y^{2}} \pm 2 K F \frac{\partial^{2} V}{\partial x \partial y} \frac{\partial^{2} w}{\partial x \partial y} \pm K F \frac{\partial^{2} V}{\partial y^{2}} \frac{\partial^{2} w}{\partial x^{2}} \pm K F \frac{\partial^{2} V}{\partial x^{2}} \frac{\partial^{2} w}{\partial y^{2}} - K V q + K V ρ t \ddot{w}] d x d y + \int_{0}^{a} \{{[2 \frac{\partial V}{\partial x} (M_{x y}) - V (\frac{\partial M_{y}}{\partial y}) + \frac{\partial V}{\partial y} (M_{y}) + 2 K F \frac{\partial V}{\partial x} (M_{x y}) + K V \frac{\partial F}{\partial y} (M_{x}) + 2 K V F (\frac{\partial M_{x y}}{\partial x}) - K F \frac{\partial V}{\partial y} (M_{x})]}_{0}^{b}\} d x + \int_{0}^{b} \{{[- V (\frac{\partial M_{x}}{\partial x}) + \frac{\partial V}{\partial x} (M_{x}) - 2 V (\frac{\partial M_{x y}}{\partial y}) - K F \frac{\partial V}{\partial y} (M_{x y}) - K V F (\frac{\partial M_{x y}}{\partial y}) - 2 K V \frac{\partial F}{\partial y} (M_{x y}) - K F \frac{\partial V}{\partial x} (M_{y}) + K V \frac{\partial F}{\partial x} (M_{y})]}_{0}^{a}\} d y,

where:

7

V = V (x, y) .

The expressions obtained in Eq. (6) contain three identically satisfied expressions: the functional of the plate problem, which is the integrand as contained in the squared bracket; and two natural boundary conditions, which are the integrands as contained in the curl brackets. These natural boundary conditions are identically satisfied at the boundary of the plate, and as such they are dropped in the further analysis in this work.

By assuming that the plate vibrates harmonically and performs sinusoidal time response, the inertia term is simplified, and the expression for the functional is as expressed in Eq. (8):

8

0 = \int_{0}^{a} \int_{0}^{b} [\frac{\partial^{2} V}{\partial x^{2}} \frac{\partial^{2} w}{\partial x^{2}} + 2 \frac{\partial^{2} V}{\partial x \partial y} \frac{\partial^{2} w}{\partial x \partial y} + \frac{\partial^{2} V}{\partial y^{2}} \frac{\partial^{2} w}{\partial y^{2}} \pm 2 K F \frac{\partial^{2} V}{\partial x \partial y} \frac{\partial^{2} w}{\partial x \partial y} \pm K F \frac{\partial^{2} V}{\partial y^{2}} \frac{\partial^{2} w}{\partial x^{2}} \pm K F \frac{\partial^{2} V}{\partial x^{2}} \frac{\partial^{2} w}{\partial y^{2}} - K V q - K V ρ t ω^{2} w] d x d y .

Furthermore, for a free vibration analysis, the lateral load $q$ is disregarded so that Eq. (8) is simplified as expressed in Eq. (9):

9

0 = \int_{0}^{a} \int_{0}^{b} [\frac{\partial^{2} V}{\partial x^{2}} \frac{\partial^{2} w}{\partial x^{2}} + 2 \frac{\partial^{2} V}{\partial x \partial y} \frac{\partial^{2} w}{\partial x \partial y} + \frac{\partial^{2} V}{\partial y^{2}} \frac{\partial^{2} w}{\partial y^{2}} \pm 2 K F \frac{\partial^{2} V}{\partial x \partial y} \frac{\partial^{2} w}{\partial x \partial y} \pm K F \frac{\partial^{2} V}{\partial y^{2}} \frac{\partial^{2} w}{\partial x^{2}} \pm K F \frac{\partial^{2} V}{\partial x^{2}} \frac{\partial^{2} w}{\partial y^{2}} - ω^{2} M K V w] d x d y,

where:

10

M = ρ * t .

The expression of Eq. (9) is a generic functional for dynamics of rectangular thin plates.

2.2. The boundary conditions

The analysis of geometrically nonlinear thin rectangular plates requires the consideration of both the out-of-plane and in-plane boundary conditions. In this study, the levy plates of simply supported-clamped-simply supported-clamped (SCSC), simply supported-clamped-simply supported-simply supported (SCSS), simply supported-simply supported-simply supported-simply supported (SSSS), simply supported-clamped-simply supported-free (SCSF), and simply supported-simply supported-simply supported-free (SSSF) rectangular plates respectively are considered. The general boundary conditions with respect to these rectangular plates are stated as given in Eq. (11-23) [17-19]:

The SCSC Rectangular plate:

11

u = v = w = w_{0} = N_{x y} = M_{x} = M_{x y} = \frac{\partial^{2} w_{0}}{\partial x^{2}} = 0, x = 0, a,

12

u = v = w = w_{0} = \frac{\partial w}{\partial y} = \frac{\partial w_{0}}{\partial y} = 0, y = 0, b .

The SCSS rectangular plate:

13

u = v = w = w_{0} = N_{x y} = M_{x} = M_{x y} = \frac{\partial^{2} w_{0}}{\partial x^{2}} = 0, x = 0, a,

14

u = v = w = w_{0} = \frac{\partial w}{\partial y} = \frac{\partial w_{0}}{\partial y} = 0, y = 0,

15

u = v = w = w_{0} = N_{y x} = M_{y} = M_{y x} = \frac{\partial^{2} w_{0}}{\partial y^{2}} = 0, y = b .

The SSSS rectangular plate:

16

u = v = w = w_{0} = N_{x y} = M_{x} = M_{x y} = \frac{\partial^{2} w_{0}}{\partial x^{2}} = 0, x = 0, a,

17

u = v = w = w_{0} = N_{y x} = M_{y} = M_{y x} = \frac{\partial^{2} w_{0}}{\partial y^{2}} = 0, y = 0, b .

The SCSF rectangular plate:

18

u = v = w = w_{0} = N_{x y} = M_{x} = M_{x y} = \frac{\partial^{2} w_{0}}{\partial x^{2}} = 0, x = 0, a,

19

u = v = w = w_{0} = \frac{\partial w}{\partial y} = \frac{\partial w_{0}}{\partial y} = 0, y = 0,

20

M_{y} = Q_{y} = N_{y} = N_{y x} = 0, y = b .

The SSSF rectangular plate:

21

u = v = w = w_{0} = N_{x y} = M_{x} = M_{x y} = \frac{\partial^{2} w_{0}}{\partial x^{2}} = 0, x = 0, a,

22

u = v = w = w_{0} = \frac{\partial w}{\partial y} = \frac{\partial w_{0}}{\partial y} = 0, y = 0,

23

M_{y} = Q_{y} = N_{y} = N_{y x} = 0, y = b .

2.3. Determination of specially energy functional

From the generic energy functional of Eq. (9), the specially energy functional with respect to any set of rectangular boundary conditions is determined by applying the general boundary conditions of Eq. (11-23). Thus, the specially energy functional (SEF) for SCSC rectangular plate is given as expressed in Eq. (24):

24

0 = \int_{0}^{a} \int_{0}^{b} [\frac{\partial^{2} V}{\partial x^{2}} \frac{\partial^{2} w}{\partial x^{2}} + 2 \frac{\partial^{2} V}{\partial x \partial y} \frac{\partial^{2} w}{\partial x \partial y} + \frac{\partial^{2} V}{\partial y^{2}} \frac{\partial^{2} w}{\partial y^{2}} + K F \frac{\partial^{2} V}{\partial x \partial y} \frac{\partial^{2} w}{\partial x \partial y} + K F \frac{\partial^{2} V}{\partial y^{2}} \frac{\partial^{2} w}{\partial x^{2}} + K F \frac{\partial^{2} V}{\partial x^{2}} \frac{\partial^{2} w}{\partial y^{2}} - ω^{2} M K V w] d x d y .

The SEF for SCSS and SSSS rectangular plates is as given by Eq. (25):

25

0 = \int_{0}^{a} \int_{0}^{b} [\frac{\partial^{2} V}{\partial x^{2}} \frac{\partial^{2} w}{\partial x^{2}} + 2 \frac{\partial^{2} V}{\partial x \partial y} \frac{\partial^{2} w}{\partial x \partial y} + \frac{\partial^{2} V}{\partial y^{2}} \frac{\partial^{2} w}{\partial y^{2}} + K F \frac{\partial^{2} V}{\partial y^{2}} \frac{\partial^{2} w}{\partial x^{2}} + K F \frac{\partial^{2} V}{\partial x^{2}} \frac{\partial^{2} w}{\partial y^{2}} - ω^{2} M K V w] d x d y .

And the SEF for SCSF and SSSF rectangular plates is as given in Eq. (26):

26

0 = \int_{0}^{a} \int_{0}^{b} [\frac{\partial^{2} V}{\partial x^{2}} \frac{\partial^{2} w}{\partial x^{2}} + 2 \frac{\partial^{2} V}{\partial x \partial y} \frac{\partial^{2} w}{\partial x \partial y} + \frac{\partial^{2} V}{\partial y^{2}} \frac{\partial^{2} w}{\partial y^{2}} + K F \frac{\partial^{2} V}{\partial y^{2}} \frac{\partial^{2} w}{\partial x^{2}} - ω^{2} M K V w] d x d y .

2.4. Development of displacement functions

Fig. 2 shows a levy plate consisting of an idealized series of orthogonal beam network in $x$ and $y$ -directions. It is assumed that each beam element running along any coordinate direction is a good representative of other series of beam elements that run along the same direction.

Fig. 2A Levy plate showing a series of orthogonal beam network and deflection configurations

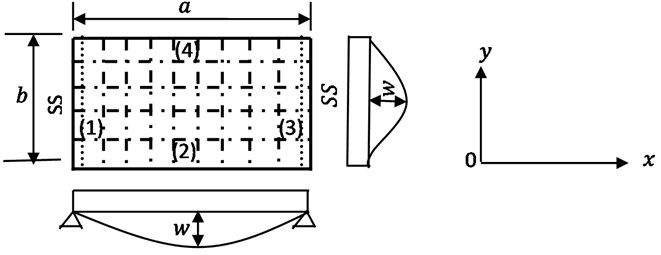
Let $w (x)$ and $w (y)$ denote the algebraic polynomial displacement functions in $x$ and $y$ -directions as expressed in Eq. (27) and Eq. (28) respectively:

27

w (x) = \sum_{i = 0}^{r} c_{i} x^{i},

28

w (y) = \sum_{j = 0}^{r} d_{j} y^{j},

where $c_{i}$ and $d_{j}$ are undetermined coefficients.

Numerically, it has been proven that a five-term polynomials provides necessary and sufficient satisfaction for completeness as shape functions for a beam element. Therefore, the value of $r$ in the summation is four. The out-of-plane boundary conditions for clamped edge, simply supported edge and free edge are as expressed in Eq. (29), Eq. (30) and Eq. (31) respectively:

29

w (∙, ∙) = w^{'} (∙, ∙) = 0,

30

w (∙, ∙) = w^{''} (∙, ∙) = 0,

31

{w^{'} (∙, ∙) = w}^{''} (∙, ∙) = w^{'''} (∙, ∙) = 0,

where $w (∙, ∙)$ represents deflection function, $w' (∙, ∙)$ , $w'' (∙, ∙)$ and $w''' (∙, ∙)$ represent first, second and third derivatives with respect to the coordinates respectively.

Suppose Fig. 2 depicts a levy plate of SCSC rectangular plate, then the deflection along $x$ -direction is expressed as given in Eq. (32):

32

w (x) = c_{o} + c_{1} x + c_{2} x^{2} + c_{3} x^{3} + c_{4} x^{4} .

By applying the boundary conditions of Eq. (30) in Eq. (32), and subsequently carrying out simplification, gives Eq. (33):

33

w (x) = c_{4} * a^{4} [(\frac{x}{a}) - 2 {(\frac{x}{a})}^{3} + {(\frac{x}{a})}^{4}] .

However, to account for series of beam mode shapes running along $y$ -direction, Eq. (33) is modified as shown in Eq. (34):

34

w (x) = c_{4} * a^{4} [{(\frac{x}{a})}^{m} - 2 {(\frac{x}{a})}^{m + 2} + {(\frac{x}{a})}^{m + 3}] .

Similarly suppose the edges Eqs. (2) and (4) of Fig. 2 are clamped, then the polynomial expression is as expressed in Eq. (35):

35

w (y) = d_{o} + d_{1} y + d_{2} y^{2} + d_{3} y^{3} + d_{4} y^{4} .

By applying the boundary conditions of Eq. (29) in Eq. (35) and after simplifying, yields Eq. (36):

36

w (y) = d_{4} * b^{4} [{(\frac{y}{b})}^{2} - 2 {(\frac{y}{b})}^{3} + {(\frac{y}{b})}^{4}] .

Also, to account for series of beam mode shapes running along $x$ -direction, Eq. (36) is modified as shown in Eq. (37):

37

w (y) = d_{4} * b^{4} [{(\frac{y}{b})}^{n + 1} - 2 {(\frac{y}{b})}^{n + 2} + {(\frac{y}{b})}^{n + 3}],

where $m$ , $n =$ 1, 2, 3, …

The rectangular plate static mode shape is the product of Eq. (34) and Eq. (37) as expressed in Eq. (38):

38

w (x, y) = A_{m n} [{(\frac{x}{a})}^{m} - 2 {(\frac{x}{a})}^{m + 2} + {(\frac{x}{a})}^{m + 3}] [{(\frac{y}{b})}^{n + 1} - 2 {(\frac{y}{b})}^{n + 2} + {(\frac{y}{b})}^{n + 3}],

where $A_{m n}$ is as expressed in Eq. (39):

39

A_{m n} = (c_{4} * a^{4}) (d_{o} * b^{4}) .

The parameter $A_{m n}$ is the amplitude of deflection function. Thus Eq. (38) is the static algebraic polynomial displacement function for SCSC rectangular plate. The same procedure is used to develop the static algebraic polynomial mode shapes for SCSS, SSSS, SCSF and SSSF rectangular plates; and they are as expressed in Eq. (40-43) respectively:

40

w (x, y) = A_{m n} [{(\frac{x}{a})}^{m} - 2 {(\frac{x}{a})}^{m + 2} + {(\frac{x}{a})}^{m + 3}] [{\frac{3}{2} (\frac{y}{b})}^{n + 1} - \frac{5}{2} {(\frac{y}{b})}^{n + 2} + {(\frac{y}{b})}^{n + 3}],

41

w (x, y) = A_{m n} [{(\frac{x}{a})}^{m} - 2 {(\frac{x}{a})}^{m + 2} + {(\frac{x}{a})}^{m + 3}] [{(\frac{y}{b})}^{n} - 2 {(\frac{y}{b})}^{n + 2} + {(\frac{y}{b})}^{n + 3}],

42

w (x, y) = A_{m n} [{(\frac{x}{a})}^{m} - 2 {(\frac{x}{a})}^{m + 2} + {(\frac{x}{a})}^{m + 3}] [{6 (\frac{y}{b})}^{n + 1} - 4 {(\frac{y}{b})}^{n + 2} + {(\frac{y}{b})}^{n + 3}],

43

w (x, y) = A_{m n} [{(\frac{x}{a})}^{m} - 2 {(\frac{x}{a})}^{m + 2} + {(\frac{x}{a})}^{m + 3}] [2 {(\frac{y}{b})}^{n} - 2 {(\frac{y}{b})}^{n + 2} + {(\frac{y}{b})}^{n + 3}] .

2.5. The stress function

One of the unknown parameters in the expression for the energy functional is the Airy’s stress function $F$ . In this work, direct integration process on compatibility Eq. (2) is used to determine the expression for stress function. Thus, a repeated integration process on the right hand side of Eq. (2) is performed four times with respect to $x$ -coordinate; and then four times with respect to $y$ -coordinate as expressed in Eq. (44):

44

F_{m n} = \int_{x}^{.} \int_{x}^{.} \int_{x}^{.} \int_{x}^{.} \int_{y}^{.} \int_{y}^{.} \int_{y}^{.} \int_{y}^{.} [{(\frac{\partial^{2} w (m n)}{\partial x \partial y})}^{2} - \frac{\partial^{2} w (m n)}{\partial x^{2}} \frac{\partial^{2} w (m n)}{\partial y^{2}}],

where $\int_{x}^{.} = \int (∙) d x$ and $\int_{y}^{.} = \int (∙) d y$ ; and for $m =$ 1, 2 and $n =$ 1, 2, 3.

In this study, the following designations for describing mode shapes are adopted: for $m = n =$ 1, then $w (1,1)$ denotes the first mode shape; for $m =$ 1 and $n =$ 2, then $w (1,2)$ denotes the second mode shape; for $m =$ 1 and $n =$ 3, then $w (1,3)$ denotes the third mode shape; and for $m =$ 2 and $n =$ 2, then $w (2,2)$ denotes the fourth mode shape. For instance, at mode 1, the mode shape with respect to SCSC rectangular plate is as given in Eq. (45):

45

w (1,1) = A_{11} [{(\frac{x}{a})}^{1} - 2 {(\frac{x}{a})}^{3} + {(\frac{x}{a})}^{4}] [{(\frac{y}{b})}^{2} - 2 {(\frac{y}{b})}^{3} + {(\frac{y}{b})}^{4}] .

Therefore, the corresponding algebraic stress function $F_{11}$ with respect to SCSC rectangular plate evaluated using Eq. (44) is as expressed in Eq. (46):

46

F_{11} = \frac{{Q A}_{11}^{2} x^{4} y^{6}}{3175200} \{x^{3} [84 - 6 y^{2} (15 + 2 (- 5 + y) y)] + 36 x^{4} [14 + 3 y (- 10 + y (10 + (- 5 + y) y))] - 42 x^{2} [14 + y (- 24 + y (21 + 2 (- 5 + y) y))] + 105 [14 + y (- 36 + y (39 + 4 (- 5 + y) y))] - 5 x^{5} [70 + y (- 144 + y (141 + 14 (- 5 + y) y))] + x^{6} [70 + y (- 144 + y (141 + 14 (- 5 + y) y))]\},

where $Q$ is as expressed in Eq. (47):

47

Q = E * t .

At any specified mode, the corresponding stress function is determined by substituting the corresponding mode shape into compatibility equation of Eq. (2); and then integrated by using Eq. (44).

2.6. Determination of amplitude of deflection

The frequency of natural vibration is a function of the rigidity parameter of the plate; and under large deflection, the plate analysis is shifted from rigid to flexible plate analysis, and the frequency depends on how much the system deviates from equilibrium position (amplitude of deflection).

The amplitude of deflection $A_{m n}$ is an unknown parameter associated with the mode shape; and to determine the amplitude of deflection, the expression for mode shape is appropriately substituted into the energy functional equation. The inertia parameter in the energy equations of Eq. (24-26) is replaced with the lateral load parameter $(K V q) .$

In this work, the mode shapes to be considered for any given set of plate boundary conditions are $w (1,1)$ , $w (1,2)$ , $w (1,3)$ and $w (2,2)$ ; and the amplitudes of deflection to be determined are $A_{11}$ , $A_{12}$ , $A_{13}$ and $A_{22}$ respectively. It is assumed that the problem system is self-adjoint. Consequently, the weighting function $V$ in the energy functional is interchanged with the deflection function $w$ without loss in generality. For instance, by letting $V = w (1,1)$ , the integral expression for evaluating the amplitude of deflection $A_{11}$ for SCSC rectangular plate is as shown in Eq. (48):

48

\int_{0}^{a} \int_{0}^{b} [{(\frac{\partial^{2} w (1,1)}{\partial x^{2}})}^{2} + 2 {(\frac{\partial^{2} w (1,1)}{\partial x \partial y})}^{2} + {(\frac{\partial^{2} w (1,1)}{\partial y^{2}})}^{2} + K F {(\frac{\partial^{2} w (1,1)}{\partial x \partial y})}^{2} + 2 K F (\frac{\partial^{2} w (1,1)}{\partial x^{2}}) (\frac{\partial^{2} w (1,1)}{\partial y^{2}})] d x d y = \int_{0}^{a} \int_{0}^{b} K q w (1,1) d x d y .

By carrying out double integration process and simplification on Eq. (48), an expression that simulates the Duffing’s type of equation is obtained as shown in Eq. (49):

49

1.3290873 * 10^{- 8} a^{4} β^{4} K Q A_{11}^{3} + [0.0393651 + 0.0185034 β^{2} + 0.00761907 β^{4}] A_{11} - {0.0066667 a}^{4} β^{4} K q = 0,

where $β = b / a$ . The solution of Eq. (49) yields three roots in terms of $A_{11}$ which are characterized with two complex roots and a real root. The real root of Eq. (49) in terms of $A_{11}$ is given as expressed in Eq. (50):

50

A_{11} = \frac{- 1.25992 ξ_{1}}{{[Z_{1} + \sqrt{Z_{2} + Z_{3} ξ_{1}^{3}}]}^{\frac{1}{3}}} + ζ_{1} \{1.99059 * 10^{7} {[Z_{1} + \sqrt{Z_{2} + Z_{3} ξ_{1}^{3}}]}^{\frac{1}{3}}\},

where:

51

ξ_{1} = (0.0393651 + 0.0185034 β^{2} + 0.00761907 β^{4}),

52

Z_{1} = 3.17964 * 10^{- 17} a^{12} K^{3} q Q^{2} β^{12},

53

Z_{2} = 1.01101 * 10^{- 33} a^{24} K^{6} q^{2} Q^{4} β^{24},

54

Z_{3} = 2.53561 * 10^{- 22} a^{12} K^{3} Q^{3} β^{12},

55

ζ_{1} = \frac{1}{a^{4} K Q β^{4}} .

Thus, the expressions for $A_{12}$ , $A_{13}$ , and $A_{22}$ are determined using the same procedure.

2.7. Determination of stiffness and mass matrices

The vibration of each mode shape of a rectangular plate consists of a product of two perpendicular motions in $x$ and $y$ -coordinates respectively. During natural vibrations, there exist modal interactions among different modes. Consequently, in this work, the mode shape $w$ and the weighting function $V$ are interactively combined to effect these modal interactions. Thus, to determine the natural frequencies, the expressions representing the energy functional of Eq. (24-26) are invoked and modified in accordance with these modal interactions as expressed in Eq. (56-58) respectively:

56

\int_{0}^{a} \int_{0}^{b} [\frac{\partial^{2} V}{\partial x^{2}} \frac{\partial^{2} w}{\partial x^{2}} + 2 \frac{\partial^{2} V}{\partial x \partial y} \frac{\partial^{2} w}{\partial x \partial y} + \frac{\partial^{2} V}{\partial y^{2}} \frac{\partial^{2} w}{\partial y^{2}} + K F_{V} F_{w} \frac{\partial^{2} V}{\partial x \partial y} \frac{\partial^{2} w}{\partial x \partial y} + K F_{V} F_{w} \frac{\partial^{2} V}{\partial y^{2}} \frac{\partial^{2} w}{\partial x^{2}} + K F_{V} F_{w} \frac{\partial^{2} V}{\partial x^{2}} \frac{\partial^{2} w}{\partial y^{2}}] d x d y = ω^{2} M K \int_{0}^{a} \int_{0}^{b} V w d x d y,

57

\int_{0}^{a} \int_{0}^{b} [\frac{\partial^{2} V}{\partial x^{2}} \frac{\partial^{2} w}{\partial x^{2}} + 2 \frac{\partial^{2} V}{\partial x \partial y} \frac{\partial^{2} w}{\partial x \partial y} + \frac{\partial^{2} V}{\partial y^{2}} \frac{\partial^{2} w}{\partial y^{2}} + K F_{V} F_{w} \frac{\partial^{2} V}{\partial y^{2}} \frac{\partial^{2} w}{\partial x^{2}} + K F_{V} F_{w} \frac{\partial^{2} V}{\partial x^{2}} \frac{\partial^{2} w}{\partial y^{2}}] d x d y = ω^{2} M K \int_{0}^{a} \int_{0}^{b} V w d x d y,

58

\int_{0}^{a} \int_{0}^{b} [\frac{\partial^{2} V}{\partial x^{2}} \frac{\partial^{2} w}{\partial x^{2}} + 2 \frac{\partial^{2} V}{\partial x \partial y} \frac{\partial^{2} w}{\partial x \partial y} + \frac{\partial^{2} V}{\partial y^{2}} \frac{\partial^{2} w}{\partial y^{2}} + K F_{V} F_{w} \frac{\partial^{2} V}{\partial y^{2}} \frac{\partial^{2} w}{\partial x^{2}}] d x d y = ω^{2} M K \int_{0}^{a} \int_{0}^{b} V w d x d y,

where $F_{V}$ and $F_{w}$ are the stress functions associated with mode shapes corresponding to weighting function and displacement function respectively. For instance, to determine the stiffness component $k_{11}$ at first mode, let $V = w = w (1,1);$ to determine the stiffness component $k_{21} = k_{12}$ , let $V = w (1,2)$ and $w = w (1,1)$ ; to determine the stiffness component $k_{31} = k_{13}$ , let $V = w (1,3)$ and $w = w (1,1)$ ; to determine the stiffness component $k_{41} = k_{14}$ , let $V = w (2,2)$ and $w = w (1,1)$ and so on. For instance, the mode shapes for SCSC plate are as expressed in Eqs. (59-62):

59

w (1,1) = A_{11} [(\frac{x}{a}) - 2 {(\frac{x}{a})}^{3} + {(\frac{x}{a})}^{4}] [{(\frac{y}{b})}^{2} - 2 {(\frac{y}{b})}^{3} + {(\frac{y}{b})}^{4}],

60

w (1,2) = A_{12} [(\frac{x}{a}) - 2 {(\frac{x}{a})}^{3} + {(\frac{x}{a})}^{4}] [{(\frac{y}{b})}^{3} - 2 {(\frac{y}{b})}^{4} + {(\frac{y}{b})}^{5}],

61

w (1,3) = A_{13} [(\frac{x}{a}) - 2 {(\frac{x}{a})}^{3} + {(\frac{x}{a})}^{4}] [{(\frac{y}{b})}^{4} - 2 {(\frac{y}{b})}^{5} + {(\frac{y}{b})}^{6}],

62

w (2,2) = A_{22} [{(\frac{x}{a})}^{2} - 2 {(\frac{x}{a})}^{4} + {(\frac{x}{a})}^{5}] [{(\frac{y}{b})}^{3} - 2 {(\frac{y}{b})}^{4} + {(\frac{y}{b})}^{5}] .

Then the stiffness matrix for SCSC rectangular plate is determined using the expressions given in Eqs. (63-67):

63

\int_{0}^{a} \int_{0}^{b} [{(\frac{\partial^{2} w (1,1)}{\partial x^{2}})}^{2} + 2 {(\frac{\partial^{2} w (1,1)}{\partial x \partial y})}^{2} + {(\frac{\partial^{2} w (1,1)}{\partial y^{2}})}^{2} + K {(F_{11})}^{2} {(\frac{\partial^{2} w (1,1)}{\partial x \partial y})}^{2} + 2 K {(F_{11})}^{2} (\frac{\partial^{2} w (1,1)}{\partial x^{2}}) (\frac{\partial^{2} w (1,1)}{\partial y^{2}})] d x d y = k_{11},

64

\int_{0}^{a} \int_{0}^{b} [\frac{\partial^{2} w (1,2)}{\partial x^{2}} \frac{\partial^{2} w (1,1)}{\partial x^{2}} + 2 \frac{\partial^{2} w (1,2)}{\partial x \partial y} \frac{\partial^{2} w (1,1)}{\partial x \partial y} + \frac{\partial^{2} w (1,2)}{\partial y^{2}} \frac{\partial^{2} w (1,1)}{\partial y^{2}} + K F_{12} F_{11} \frac{\partial^{2} w (1,2)}{\partial x \partial y} \frac{\partial^{2} w (1,1)}{\partial x \partial y} + K F_{12} F_{11} \frac{\partial^{2} w (1,2)}{\partial y^{2}} \frac{\partial^{2} w (1,1)}{\partial x^{2}} + K {F_{12} F}_{11} \frac{\partial^{2} w (1,2)}{\partial x^{2}} \frac{\partial^{2} w (1,1)}{\partial y^{2}}] d x d y = k_{21} = k_{12},

65

\int_{0}^{a} \int_{0}^{b} [\frac{\partial^{2} w (1,3)}{\partial x^{2}} \frac{\partial^{2} w (1,1)}{\partial x^{2}} + 2 \frac{\partial^{2} w (1,3)}{\partial x \partial y} \frac{\partial^{2} w (1,1)}{\partial x \partial y} + \frac{\partial^{2} w (1,3)}{\partial y^{2}} \frac{\partial^{2} w (1,1)}{\partial y^{2}} + K F_{13} F_{11} \frac{\partial^{2} w (1,3)}{\partial x \partial y} \frac{\partial^{2} w (1,1)}{\partial x \partial y} + K F_{13} F_{11} \frac{\partial^{2} w (1,3)}{\partial y^{2}} \frac{\partial^{2} w (1,1)}{\partial x^{2}} + K F_{13} F_{11} \frac{\partial^{2} w (1,3)}{\partial x^{2}} \frac{\partial^{2} w (1,1)}{\partial y^{2}}] d x d y = k_{31} = k_{13},

66

\int_{0}^{a} \int_{0}^{b} [\frac{\partial^{2} w (2,2)}{\partial x^{2}} \frac{\partial^{2} w (1,1)}{\partial x^{2}} + 2 \frac{\partial^{2} w (2,2)}{\partial x \partial y} \frac{\partial^{2} w (1,1)}{\partial x \partial y} + \frac{\partial^{2} w (2,2)}{\partial y^{2}} \frac{\partial^{2} w (1,1)}{\partial y^{2}} + K F_{22} F_{11} \frac{\partial^{2} w (2,2)}{\partial x \partial y} \frac{\partial^{2} w (1,1)}{\partial x \partial y} + K F_{22} F_{11} \frac{\partial^{2} w (2,2)}{\partial y^{2}} \frac{\partial^{2} w (1,1)}{\partial x^{2}} + K F_{22} F_{11} \frac{\partial^{2} w (2,2)}{\partial x^{2}} \frac{\partial^{2} w (1,1)}{\partial y^{2}}] d x d y = k_{41} = k_{14},

67

\int_{0}^{a} \int_{0}^{b} [{(\frac{\partial^{2} w (2,2)}{\partial x^{2}})}^{2} + 2 {(\frac{\partial^{2} w (2,2)}{\partial x \partial y})}^{2} + {(\frac{\partial^{2} w (2,2)}{\partial y^{2}})}^{2} + K {(F_{22})}^{2} {(\frac{\partial^{2} w (2,2)}{\partial x \partial y})}^{2} + 2 K {(F_{22})}^{2} (\frac{\partial^{2} w (2,2)}{\partial x^{2}}) (\frac{\partial^{2} w (2,2)}{\partial y^{2}})] d x d y = k_{44} .

The resulting stiffness matrix is given as expressed in Eq. (68):

68

[K] = [\begin{matrix} k_{11} k_{12} k_{13} k_{14} \\ k_{21} k_{22} k_{23} k_{24} \\ k_{31} k_{32} k_{33} k_{34} \\ k_{41} k_{42} k_{43} k_{44} \end{matrix}] .

The same procedure is used to develop other required stiffness matrices for SCSS, SSSS, SCSF and SSSF respectively. In similar approach, the right hand side (RHS) of Eq. (56), Eq. (57) and Eq. (58) respectively will yield the mass matrices after due integration process. Thus, for SCSC rectangular plate, the mass matrix is determined by using expressions given in Eqs. (69-72):

69

ω^{2} M K \int_{0}^{a} \int_{0}^{b} [{(w (1,1))}^{2}] d x d y = b_{11},

70

ω^{2} M K \int_{0}^{a} \int_{0}^{b} [w (1,2) * w (1,1)] d x d y = b_{21} = b_{12},

71

ω^{2} M K \int_{0}^{a} \int_{0}^{b} [w (1,3) * w (1,1)] d x d y = b_{31} = b_{13},

72

ω^{2} M K \int_{0}^{a} \int_{0}^{b} [{(w (2,2))}^{2}] d x d y = b_{44} .

The resulting mass matrix is as given in Eq. (73):

73

[B] = ω^{2} [\begin{matrix} b_{11} b_{12} b_{13} b_{14} \\ b_{21} b_{22} b_{23} b_{24} \\ b_{31} b_{32} b_{33} b_{34} \\ b_{41} b_{42} b_{43} b_{44} \end{matrix}] M K .

The same approach is used to develop the mass matrices for SCSS, SSSS, SCSF and SSSF respectively.

3. Numerical evaluation and discussion of results

Natural vibrations of rectangular isotropic plates under geometrical nonlinearity are studied in this paper using weak-form variational principle. Numerical evaluations are required for adequate validation of the results of the present study with the results found in existing literature. The plate parameters used in this study are: $E =$ 10.92 MPa, $ρ =$ 100 kgm^-3, $μ =$ 0.3, $a =$ 1.0 m, $t =$ 0.01 m, $b =$ open, and $β = b / a$ ,which were previously used by [3, 11, 20, 21] in their separate studies using different approximation techniques. Thus, by using aspect ratio, $β = 1$ , these parameters were appropriately substituted and the numerical values for the elements in the stiffness matrix of Eq. (68) are as given in Eq. (74):

74

[K] = [\begin{matrix} 0.0632071 0.0415130 0.0221544 0.0289220 \\ 0.0415130 0.0419203 0.0288422 0.0292578 \\ 0.0221544 0.0288422 0.0235024 0.0201416 \\ 0.0289220 0.0292578 0.0201416 0.0293874 \end{matrix}] .

Similarly, by substituting these parameters appropriately, the numerical values for the elements in the mass matrix of Eq. (73) are as given in Eq. (75):

75

[B] = ω^{2} [\begin{matrix} 7.46967 4.93073 2.62527 3.44405 \\ 4.93073 3.55067 2.02177 2.48009 \\ 2.62527 2.02177 1.21446 1.41218 \\ 3.44405 2.48009 1.41218 1.96091 \end{matrix}] 10^{- 5} .

In the matrix manipulation, suppose the difference between $[K]$ and $[B]$ is $[A]$ , then:

76

[A] = [K] - [B] .

The determinant of $[A]$ is thus:

77

d e t ([A]) = d e t ([K] - [B]) .

For nontrivial solution of the eigen-function, Eq. (77) is set equal to zero, as expressed in Eq. (78):

78

d e t ([K] - [B]) = 0 .

The expression of Eq. (78) can be simplified numerically by pre-multiplying Eq. (78) by the inverse of Eq. (75) as expressed in Eq. (79):

79

d e t ({[B]}^{- 1} [K] - {[B]}^{- 1} [B]) = 0 .

The result of the manipulation of Eq. (79) yields an expression as given in Eq. (80):

80

d e t [\begin{matrix} (1323.27 - R) & - 2441.51 & 2584.17 & - 1723.73 \\ - 1482.14 & (4108.7 - R) & - 13388.7 & 177.234 \\ 1468.96 & 824.251 & (18640.5 - R) & 536.425 \\ - 32.5375 & - 9.94004 & - 2.26802 & (3915.67 - R) \end{matrix}] = 0,

where $R$ is $R = ω^{2} .$

The solution of the resulting quartic algebraic equation in terms of R and subsequently in terms of $ω$ gives the nonlinear natural frequencies of vibration of the rectangular SCSC plate at aspect ratio equal to one. Therefore, by carrying out the same procedure with respect to each of the SCSS, SSSS, SCSF and SSSF rectangular plates respectively yields the desired natural frequencies for the respective rectangular plate up to first four lowest natural frequencies.

However, Table 1 presents the numerical values of the variation of the amplitudes of plate deflection with aspect ratios for the SCSC, SCSS, SSSS, SCSF and SSSF rectangular plates. The amplitudes of deflection are the measures of the rigidity characteristics of rectangular plates; and under geometrical nonlinearity of rectangular plates, these geometric characteristics shift from rigid to flexible plate conditions [21]. The amplitudes of deflection are strong parameters that affect the nonlinear flexural frequencies of rectangular plates based on large deflection.

From Table 1, it was observed that the amplitudes of deflection for the SCSC, SCSS, SSSS and SSSF rectangular plates exhibit hard-spring type with the aspect ratios; but with the exception of the amplitudes of deflection of the third mode of the SSSF rectangular plate boundary conditions, which exhibit soft-spring type. On the other hand, it was observed that the amplitudes of deflection for the SCSF rectangular plate boundary conditions exhibit entirely soft-spring type with the aspect ratios.

Also, Table 2 presents the numerical values of nonlinear natural frequencies for the SCSC, SCSS, SSSS, SCSF and SSSF rectangular plates based on the above given plate parameters at various aspect ratios.

Table 1Variation of amplitudes of deflection with aspect ratios

Boundary condition	Amplitude of deflection, $A_{m n}$
	Mode	Aspect ratio, $β$
	Mode	$β =$ 0.25	$β =$ 0.50	$β =$ 0.75	$β =$ 1.0	$β =$ 1.25	$β =$ 1.50
SCSC	$A_{11}$	0.0063	0.0919	0.3960	0.9779	1.6535	2.1545
	$A_{12}$	0.0074	0.1102	0.4925	1.2911	2.3935	3.4001
	$A_{13}$	0.0064	0.0974	0.4527	1.2603	2.5691	4.1174
	$A_{22}$	0.0130	0.1863	0.7711	1.8036	3.0012	4.0434
SCSS	$A_{11}$	0.0061	0.0824	0.3160	0.6845	1.0382	1.2800
	$A_{12}$	0.0054	0.0760	0.3106	0.7364	1.2454	1.6731
	$A_{13}$	0.0032	0.0477	0.2116	0.5574	1.0770	1.6642
	$A_{22}$	0.0094	0.1242	0.4556	0.9455	1.4380	1.8363
SSSS	$A_{11}$	0.0057	0.0664	0.2121	0.3788	0.4955	0.5639
	$A_{12}$	0.0034	0.0466	0.1837	0.4140	0.6552	0.8314
	$A_{13}$	0.0020	0.0287	0.1253	0.3220	0.6009	0.8879
	$A_{22}$	0.0059	0.0750	0.2604	0.5091	0.7352	0.9036
SCSF	$A_{11}$	11.4724	4.2488	2.8316	2.3019	2.0428	1.8960
	$A_{12}$	4.8839	1.6481	1.0031	0.7499	0.6163	0.5327
	$A_{13}$	7.1802	2.1422	1.1845	0.8296	0.6509	0.5432
	$A_{22}$	9.8596	3.6792	2.4892	2.0541	1.8455	1.7292
SSSF	$A_{11}$	0.0159	0.1105	0.2136	0.2743	0.3065	0.3247
	$A_{12}$	0.0116	0.0926	0.2107	0.3089	0.3768	0.4218
	$A_{13}$	15.2944	5.3778	3.3720	2.5797	2.1637	1.9087
	$A_{22}$	0.0181	0.1085	0.1924	0.2425	0.2713	0.2887

Table 2The numerical values of nonlinear natural frequencies of isotropic levy plates at various aspect ratios

Boundary condition	Nonlinear natural frequency, (rad/sec)
	Mode	Aspect ratio, $β$
	Mode	$β =$ 0.25	$β =$ 0.50	$β =$ 0.75	$β =$ 1.0	$β =$ 1.25	$β =$ 1.50
SCSC	$ω_{11}$	363.497	95.2656	45.9213	29.0854	23.2362	22.5013
	$ω_{12}$	473.004	139.173	80.9642	62.6300	50.0136	42.5369
	$ω_{13}$	1013.780	258.712	118.987	70.3803	56.2073	60.022
	$ω_{22}$	2049.33	517.789	234.221	135.156	90.7409	71.5289
SCSS	$ω_{11}$	254.198	69.3414	35.3535	23.7843	19.653	19.2091
	$ω_{12}$	366.991	118.946	75.0828	60.2854	42.7581	33.7225
	$ω_{13}$	838.929	215.700	100.381	60.6915	54.8403	53.8604
	$ω_{22}$	2058.11	520.456	235.745	136.163	90.1307	66.3526
SSSS	$ω_{11}$	167.815	49.357	27.454	20.5135	19.3654	19.5027
	$ω_{12}$	315.027	106.266	69.7313	54.209	40.8385	33.850
	$ω_{13}$	713.114	185.143	87.458	57.9053	54.0947	56.3444
	$ω_{22}$	1862.55	471.88	214.423	124.733	82.6781	59.174
SCSF	$ω_{11}$	47.7087	19.6398	14.874	14.3069	13.9204	13.471
	$ω_{12}$	116.163	59.5027	43.8963	35.6418	35.2985	35.6283
	$ω_{13}$	267.400	78.6609	50.5387	48.853	54.5767 – 0.8225i	53.918 – 5.7295i
	$ω_{22}$	991.382	257.027	122.055	76.6943	54.5767 + 0.8225i	53.918 + 5.7295i
SSSF	$ω_{11}$	0 + 10472.4i	0 + 2588.97i	0 + 1531.26i	0 + 1194.23i	0 + 1044.08i	0 + 965.899i
	$ω_{12}$	42.6735	18.8572	14.1528	12.7282	12.169	11.7224
	$ω_{13}$	103.498	58.4575	45.4109	33.2682	31.362	33.8029
	$ω_{22}$	305.628	86.0388	50.3588	47.5902	46.406	45.960

From Table 2, it was observed that the nonlinear natural frequencies for the levy plates under investigation exhibit soft-spring type with aspect ratios, except at the third modes of SCSC and SSSS rectangular plates, which deviated from the norm at aspect ratios 1.25 and 1.5 respectively. Furthermore, it was observed that the SCSF rectangular plate boundary conditions yielded positive real-valued complex conjugate nonlinear natural frequencies at the third and fourth modes in the vicinity of aspect ratios of 1.25 and 1.5 respectively. This exposition significantly doubts the stability of the SCSF rectangular plate boundary conditions at third and fourth modes at aspect ratio greater or equal to 1.25 based on the existence of high positive value of the real part of the complex conjugates. However, at aspect ratios less than or equal to 1.0, the SCSF rectangular plate boundary conditions yielded distinct positive nonlinear natural frequencies at the same third and fourth modes respectively. This exposition signifies that within the vicinity of the identified aspect ratios, the SCSF rectangular plate is stable at the third and fourth modes respectively. Also, from Table 2, it was observed that the SSSF rectangular plate boundary conditions yielded positive pure imaginary nonlinear natural frequencies at the first mode for all the selected aspect ratios, which means that the SSSF plate boundary conditions exhibits critical behaviour at the first mode, otherwise it is said to be merely stable. This exposition signifies that in the geometrically nonlinear dynamic analysis of SSSF rectangular plate boundary conditions using modal combination approach, the fundamental nonlinear frequency is sought at second mode instead of the first mode vis-à-vis the linear fundamental frequency of the plate boundary conditions.

Table 3 presents the comparison of the nonlinear fundamental frequencies of the present study’s results with the results found in literature. However, the restriction to the use of only the nonlinear fundamental frequencies for the comparison was due to the non-availability of the results for higher mode nonlinear natural frequencies in almost all the literature reviewed.

Table 3Comparison of Nonlinear fundamental frequencies with results found in literature (β= 1)

Plate properties	Boundary condition	Investigator	Fundamental frequency (rad/s)	Percentage error
$E =$ 10.92 MPa; $ρ =$ 100 kg/m³ $μ =$ 0.3 $a =$ 1.0 m $b =$ 1.0 m $t =$ 0.01 m	SCSC	Present study	29.0854
		[20]	29.1873	0.349
		[3]	29.2315	0.500
		[11]	29.2627	0.606
	SSSS	Present study	20.5135
		[20]	20.0990	–2.062
		[3]	20.0916	–2.100
		[11]	20.0818	–2.150
	SCSS	Present study	23.7843
		[20]	24.0308	1.026
		[3]	24.0113	0.943
		[11]	23.9717	0.782
$E =$ 30 GPa $ρ =$ 25 kg/m³ $μ =$ 0.3 $a =$ 10 m $b =$ 10 m $t =$ 0.2 m	SSSS	Present study	422.785
	SSSS	[23]	421.3570	–0.339
	SCSF	Present study	293.666
	SCSF	[23]	295.1590	0.506
	SSSF	Present study	261.982
	SSSF	[23]	261.2294	–0.288

From Table 3, it was observed from columns 4 and 5 that the present study’s results exhibit lower-bound with respect to the results found in literature for the SCSC, SCSS and SCSF rectangular plates respectively. But in the case of SSSS and SSSF rectangular plates, the present study’s results exhibit upper-bound with respect to the results found in literature. Also, from column 5 of Table 3, the calculated absolute mean percentage error is 0.186, which shows that the present study’s results are in good agreement with the results found in literature.

4. Conclusions

This paper evaluates the nonlinear natural frequencies for Levy plates using weak-form variational principle in algebraic orthogonal polynomial displacement functions. The nonlinear fundamental frequencies evaluated in this work are in good agreement with the results found in literature that were evaluated using other approximation techniques such as the finite element methods. Therefore, it is here-upon concluded that the efficacy of weak-form variational principle technique in dynamic analysis of Levy plates is very satisfactory vis-à-vis other approximation techniques. Also, it is here-unto concluded that the use of algebraic polynomial shape functions in vibration analysis of Levy plates yields satisfactory approximations to all the boundary conditions of the plates. Furthermore, it was observed in this work that the nonlinear natural frequencies for SCSF rectangular plate boundary conditions in the third and fourth modes exhibited positive real valued complex conjugates at aspect ratios 1.25 and 1.50 respectively. Thus, it is here concluded that at aspect ratio greater than or equal to 1.25 in the third and fourth modes respectively, the motions of vibration of SCSF rectangular plate are not stable under geometrically nonlinear conditions. Also, it was observed that the nonlinear natural frequencies in the first mode at various aspect ratios for SSSF rectangular plate exhibited positive pure imaginary values. The exposition here shows that at first mode, the nonlinear motion of vibration for SSSF rectangular plate under modal combination analysis is pole centred, otherwise it is said to exhibit critical behaviour or it is merely stable at the first mode. Therefore, it is here concluded that using modal combination analysis, the nonlinear fundamental frequency for SSSF rectangular plate is ought to be sought in the second mode instead of the usual first mode.

References

Yoowattana T., Chantarawichit P., Vibooljak J., Sompornjaroensuk Y. Accurate approximate and analytical methods for vibration and bending problems of plates: a literature survey. Applied Mathematical Sciences, Vol. 9, Issue 35, 2015, p. 1697-1719.

Publisher
Crawford J., Atluri S. Non-linear vibrations of flat plate with initial stresses. Journal of Sound and Vibration, Vol. 43, Issue 1, 1975, p. 117-129.

Publisher
Rao Raju G. V. I. S., Raju K. K. A finite element formulation for large amplitude flexural vibrations of thin rectangular plates. Computers and Structures, Vol. 6, 1976, p. 163-167.

Publisher
Han W., Petyt M. Geometrically nonlinear vibration analysis of thin, rectangular plates using the hierarchical finite element method – I: The fundamental mode of isotropic plates. Computers and Structures, Vol. 63, Issue 2, 1997, p. 295-308.

Publisher
Singha M. K., Daipa R. Nonlinear vibration of symmetrically laminated composite skew plates by finite element method. International Journal of Nonlinear Mechanics, Vol. 42, 2007, p. 1144-1152.

Publisher
Hui D. Soft-spring nonlinear vibrations of antisymmetrically laminated rectangular plates. International Journal of Mechanical Sciences, Vol. 27, Issue 6, 1985, p. 397-408.

Publisher
Xiang Y., Zhao Y. B., Wei G. W. Levy solutions for vibration of multi-span rectangular plates. International Journal of Mechanical Sciences, Vol. 44, 2002, p. 1195-1218.

Publisher
Saha K. N., Misra D., Ghosal S., Pohit G. Nonlinear free vibration analysis of square plates with various boundary conditions. Journal of Sound and Vibration, Vol. 287, 2005, p. 1031-1044.

Publisher
Bugaru M., Vasile O. Nonlinear dynamic behaviour of thin rectangular plates parametrically excited using the asymptotic method, Part 1: Computation of the amplitude. Proceedings of the 10th WSEAS International Conference on Applied Mathematics, Dallas, Texas, USA, 2006, p. 488-492.

Search CrossRef
Shooshtari A., Khadem S. E. A multiple scale method solution for the nonlinear vibration of rectangular plates. Scientia Iranica, Vol. 14, Issue 1, 2007, p. 64-71.

Search CrossRef
Wu W. X., Shu C., Wang C. M. Mesh-free least squares-based finite difference method for large amplitude free vibration analysis of arbitrarily shaped thin plates. Journal of Sound and Vibration, Vol. 317, 2008, p. 955-974.

Publisher
Lynda B., Fayçal M. A first order finite element theory for free vibration of composite plates. International Review of Mechanical Engineering, Vol. 5, Issue 3, 2011, p. 459-464.

Search CrossRef
Hao Y. X., Zhang W., Yang J., Li S. Y. Nonlinear dynamic response of a simply supported rectangular functionally graded material plate under the time-dependent thermalmechanical loads. Journal of Mechanical Science and Technology, Vol. 25, Issue 7, 2011, p. 1637-1646.

Publisher
Hashemi S., Jaberzadeh E. A finite strip formulation for nonlinear free vibration of plates. 15th World Conference on Earthquake Engineering, 2012.

Search CrossRef
Jameel A. N., Hussien R. M. Vibration analysis of laminated composite plate under thermo-mechanical loading. Journal of Engineering, Vol. 20, Issue 2, 2014, p. 118-135.

Publisher
Mama B. O., Onah H. N., Ike C. C., Osadebe N. N. Solution of free harmonic vibration equation of simply supported Kirchhoff plate by Galerkin-Vlasov method. Nigerian Journal of Technology, Vol. 36, Issue 2, 2017, p. 361-365.

Publisher
Chia C. Y. Nonlinear Analysis of Plates. McGraw-Hill International Book Company, USA, 1980.

Search CrossRef
Szilard R. Theories and Applications of Plate Analysis. John Wiley and Sons, USA, 2004.

Publisher
Amabili M. Nonlinear Vibrations and Stability of Shells and Plates. Cambridge University Press, New York, USA, 2008.

Publisher
Mei C. Finite element displacement method for large amplitude free flexural vibrations of beams and plates. Computers and Structures, Vol. 3, 1973, p. 163-174.

Publisher
Wah T. Large amplitude flexural vibration of rectangular plates. International Journal of Mechanical Sciences, Vol. 5, 1963, p. 425-438.

Publisher
Vol’mir A. S. The Nonlinear Dynamics of Plates and Shells. National Technical Information Services, U. S. Department of Commerce, 1974.

Search CrossRef
Silva F. M. A., Pinho F. A. X., Delprado Z. J. G., Goncalves P. D. On the Galerkin-iterative method to the nonlinear vibrations of rectangular plates. 10th Conferencia Brasileria de Dinamica, Controle e Aplicacoes, 2011, p. 140-143.

Publisher

About this article

Received

06 December 2019

Accepted

17 December 2019

Published

31 December 2019

DOI

https://doi.org/10.21595/mme.2019.21212

Keywords

algebraic polynomial

amplitude of deflection

energy functional

levy plate

nonlinear natural frequency

weak-form

variational principle

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2019 11 28

Free vibration analysis of simply supported rectangular plates

Ganesh Naik Guguloth, Baij Nath Singh, Vinayak Ranjan

Research article

2019 05 15

Free vibration of a Levy-type solution for plates based on two-variable refined plate theory by using SEM

Shota Kiryu, Sofia W. Alisjahbana, Irene Alisjahbana, Mitsuo Nagao, Buntara S. Gan

Research article

2018 12 13

Analysis of free vibration of nano plate resting on Winkler foundation

Piyush Pratap Singh, Mohammad Sikandar Azam, Vinayak Ranjan

Research article

2018 03 31

Kantorovich variational method for the flexural analysis of CSCS Kirchhoff-Love plates

Charles Chinwuba Ike, Benjamin Okwudili Mama

P. D. Onodagu, V. O. Okonkwo, and C. H. Aginam, “Nonlinear free vibration analysis of levy plates using weak-form variational principle in polynomial displacement functions,” Mathematical Models in Engineering, Vol. 5, No. 4, pp. 158–174, Dec. 2019, https://doi.org/10.21595/mme.2019.21212

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/mme.2019.21212
UR  - https://doi.org/10.21595/mme.2019.21212
TI  - Nonlinear free vibration analysis of levy plates using weak-form variational principle in polynomial displacement functions
T2  - Mathematical Models in Engineering
AU  - Onodagu, P. D.
AU  - Okonkwo, V. O.
AU  - Aginam, C. H.
PY  - 2019
DA  - 2019/12/31
PB  - JVE International Ltd.
SP  - 158-174
IS  - 4
VL  - 5
SN  - 2351-5279
SN  - 2424-4627
ER  - 

Copy Ris

Copied to clipboard!

@article{Onodagu_2019,
	doi = {10.21595/mme.2019.21212},
	url = {https://doi.org/10.21595/mme.2019.21212},
	year = 2019,
	month = {dec},
	publisher = {{JVE} International Ltd.},
	volume = {5},
	number = {4},
	pages = {158--174},
	author = {P. D. Onodagu and V. O. Okonkwo and C. H. Aginam},
	title = {Nonlinear free vibration analysis of levy plates using weak-form variational principle in polynomial displacement functions},
	journal = {Mathematical Models in Engineering}
}

Copy Bibtex

Copied to clipboard!

[1]P. D. Onodagu, V. O. Okonkwo, and C. H. Aginam, “Nonlinear free vibration analysis of levy plates using weak-form variational principle in polynomial displacement functions,” Mathematical Models in Engineering, vol. 5, no. 4, pp. 158–174, Dec. 2019, doi: 10.21595/mme.2019.21212.

Copy IEEE

Copied to clipboard!

Onodagu, P. D., V. O. Okonkwo, and C. H. Aginam. “Nonlinear Free Vibration Analysis of Levy Plates Using Weak-Form Variational Principle in Polynomial Displacement Functions.” Mathematical Models in Engineering 5, no. 4 (December 31, 2019): 158–74. https://doi.org/10.21595/mme.2019.21212.

Copy Chicago

Copied to clipboard!

Nonlinear free vibration analysis of levy plates using weak-form variational principle in polynomial displacement functions

Abstract

1. Introduction

1.1. Related works

1.2. Statement of problem and objectives

2. Theoretical formulations

2.1. Formulation of energy functional

2.2. The boundary conditions

2.3. Determination of specially energy functional

2.4. Development of displacement functions

2.5. The stress function

2.6. Determination of amplitude of deflection

2.7. Determination of stiffness and mass matrices

3. Numerical evaluation and discussion of results

4. Conclusions

References

About this article

Related Articles