Bearing fault identification based on ASMOTE-CFR

Cheng, Huanke; Wang, Ping; Wang, Guangbin; Lv, Ying

doi:10.21595/vp.2020.21520

Vibroengineering Procedia

Browse Procedia

Published: 29 June 2020

Check for updates

Bearing fault identification based on ASMOTE-CFR

Huanke Cheng¹

Ping Wang²

Guangbin Wang³

Ying Lv⁴

¹Hunan University of Science and Technology, Hunan Provincial Key Laboratory of Mechanical Equipment Health, Xiangtan, China

²Hunan Power Machinery Research Institute of AECC, Zhuzhou, China

^{3, 4}College of Mechanical Engineering, Lingnan Normal University, Zhanjiang, 524048, China

Corresponding Author:

Guangbin Wang

Cite the article Download PDF

Downloads 1058

Abstract

Aiming at the problem of data unbalance caused by the lack of bearing failure test data, the paper proposes a collaborative filtering recommendation (CFR) method for adaptive Smote (ASMOTE) resampling and matrix decomposition of minority samples (ASMOTE-CFR). The method first adopts adaptive Smote method to synthesize different number of new sample equalization test data sets according to the data distribution. and then a variety of typical feature values such as time domain, frequency domain, time frequency domain, etc. are extracted to obtain the bearing feature matrix, and then a scoring matrix that accurately describes the bearing state is designed and based on the matrix Based on the decomposed collaborative filtering algorithm, a set of collaborative filtering recommendation system for bearing state recognition is proposed. Using this method, different forms of fault data on the outer ring of the rolling bearing were identified and verified. The accuracy of identification reached more than 98 %. Compared with the recognition accuracy of the collaborative filtering recommendation algorithm, this method improved 8 %.

1. Introduction

During the operation of the wind turbine, bearing failure is the main failure of the wind turbine. If the timeliness of finding the bearing failure cannot be guaranteed, the operating life of the entire generator set will be greatly reduced, or even cause a major safety accident, so how to effectively identify the bearing The fault state has become one of the main contents in the field of fault diagnosis.

Motor bearings will generate huge amounts of data during monitoring. Normally, the normal sample data will be much larger than the fault sample. In recent years, many scholars have carried out research to improve the imbalanced learning problem [1-4]. Sampling Random Oversampling randomly copies a few samples to balance the class distribution; Jose et al. [5] proposed a Smote oversampling method. This method is not simply to copy its samples but there is a synthetic sample mechanism blindly so that the learning of samples is easy to cause overfitting.

At present, Collaborative Filtering (CF) is one of the most commonly used methods in the field of recommendation systems. The core idea is to predict user preferences through rating information of similar users or similar items [2, 6]. The paper [7-9] proposed a probabilistic matrix decomposition model, which describes the matrix decomposition process from the perspective of the probability generation process, effectively alleviating the problem of data sparsity.

Aiming at the difficulty of designing the scoring matrix of the recommendation system in the field of fault diagnosis, this paper first extracts the typical features from the time domain, frequency domain, and time-frequency domain to obtain the bearing feature matrix, and then constructs a set of accurate scoring matrices for the bearing state. Two matrixes with different characteristics are organically combined to obtain a joint scoring matrix for bearing state recognition. Based on the matrix filtering collaborative filtering algorithm and gradient descent optimization algorithm, a set of collaborative filtering recommendation systems for bearing state recognition is proposed.

2. CFR system based on ASMOTE

2.1. Adaptive smote oversampling method (ASMOTE)

This article sets the number of new minority samples to be generated according to the balance of data distribution. The specific algorithm flow is as follows:

Step 1: Calculate the degree of unbalance. Recall that the minority sample is $X_{s}$ and the majority is $X_{m}$ , then the imbalance:

1

d = \frac{X_{s}}{X_{m}}, d \in (0,1) .

Step 2: Calculate the number of samples to be synthesized:

2

G = (X_{m} - X_{s}) * b, b \in (0,1),

where $b \in (0,1)$ is a parameter used to specify the desired balance level after generation of the synthetic data.

Step 3: For each sample $X$ that belongs to the minority class, calculate the $X = {X_{1}, X_{2}, \dots, X_{n}}$ neighbors with Euclidean distance, $Δ i$ is the number of samples belonging to the majority class among the $k$ neighbors, and the ratio $r$ is $r = Δ i / k$ , $i =$ 1, 2,…, $X_{s}$ , $r \in (0,1)$ , where $Δ i$ is the number of examples in the $k$ nearest neighbors of $x_{i}$ that belong to the majority class.

Step 4: Normalize $r_{i}$ for each minority sample obtained in Eq. (3):

3

r_{i} = \frac{r_{i}}{\sum_{i = 1}^{m s} r_{i}} .

Step 5: Calculate the number of synthesized samples for each minority sample:

4

g_{i} = r_{i} \times G .

Step 6: Randomly choose one minority data example, $x_{z i}$ , from the $K$ nearest neigh bors for data $x_{i}$ . and synthesize according to the following equation:

5

s_{i} = x_{i} + (x_{z i} - x_{i}) \times λ .

Repeat the synthesis until the number of synthesis required by Eq. (5) is satisfied.

2.2. Collaborative filtering recommendation algorithm based on matrix decomposition

The idea of the collaborative filtering algorithm based on matrix decomposition is to decompose the higher-dimensional “user-movie” rating matrix into the product of two lower-dimensional matrices. These two low-dimensional matrices are the user latent factor matrix and Project latent factor matrix, where $k$ is the number of latent factor features, as shown in Eq. (6):

6

R_{m n} \approx P_{k m} * Q_{k n}^{T} .

For the existing $n$ score records, the square of error is used to calculate the loss function of each score. The specific formula is as follows:

7

L (P, Q, R) = \frac{1}{n} \sum L (P^{j}, Q^{i}, R_{i}^{(j)}) = \frac{1}{n} {\sum (R_{i}^{(j)} - R_{i}^{(j)})}^{2} .

To prevent overfitting, regularization terms are added to the overall loss function:

8

L = a r g m i n (L (P, Q, R) + λ ({‖P‖}^{2} + {‖Q‖}^{2})),

where $λ$ is the regularization coefficient, further, the gradient descent method is used to deal with the minimization problem, the core problem of the matrix factorization model is to minimize the overall loss function of the above formula by finding the appropriate parameters $P$ and $Q$ .

3. Bearing fault identification based on ASMOTE-CFR

ASMOTE-CFR is based on the unbalance of data in massive data. First, the ASMOTE algorithm is used to equalize a few samples of faulty bearings. Further combined with the CFR method to design specific scoring rules to establish the corresponding scoring matrix, so as to effectively solve the problem of low accuracy in unbalanced data sets. Then extract the typical characteristic values in the time domain, the fuzzy entropy value in the frequency domain and the wavelet packet entropy value in the frequency domain to obtain the bearing feature matrix, and then design a scoring matrix that accurately describes the bearing state. Finally, these two matrices with different characteristics are organically Combined, a joint scoring matrix for bearing status identification is obtained. Based on the joint scoring matrix, the bearing status is effectively identified.

Suppose there are signal data of $u$ group of rolling bearings $(S^{1}, S^{1}, \dots, S^{k}, S^{k + 1}, \dots, S^{u - 1}, S^{u})$ and there are $v$ different types of states) $(Z_{1}, Z_{2}, Z_{3}, \dots, Z_{v})$ . In the signal data of group $u$ rolling bearings, it is assumed that the set of minority samples is $X_{s} = {X_{1}, X_{2}, \dots, X_{n}}$ , the set of majority samples is $X_{m} = {X_{1}, X_{2}, \dots, X_{m}}$ , $X_{n}$ represents the feature vector of the $n$ minority sample, and $X_{m}$ represents the feature vector of the $m$ majority sample. and here $(m + n \leq u)$ . Calculate the number of samples to be synthesized by $G = (X_{m} - X_{s}) * b$ , $b \in (0,1)$ , and for the minority sample $X_{s}$ , use the Euclidean distance to calculate the $h$ nearest neighbor, and then randomly choose one minority data example, $x_{z i}$ ,from the $h$ nearest neigh bors for data $x_{i}$ and synthesize according to $S_{i} = X_{s} + (X_{s} - X_{i}) \times λ$ . The sample data after ASMOTE will increase by certain percentage. Assuming that the data after ASMOTE has $w$ group, the state of the previous $k$ group of training data $S^{1}, S^{1}, \dots, S^{k}$ is known, and now the CFR is used to identify the state of the $w - k + 1$ group of test data. $S^{k + 1}, \dots, S^{w} .$

In the $i$ group of data, 17 features are extracted in the time domain, which are average, root mean square value, root square amplitude, rectified average, kurtosis, variance, maximum, minimum, peak-to-peak value, Standard deviation, waveform index, peak index, pulse index, margin index, skewness index, kurtosis index. Frequency domain extraction fuzzy entropy and sample entropy, time-frequency domain extraction wavelet packet energy entropy and EMD decomposition into 12 Each order component IMF entropy extracts a total of 32 mixed domain features.

The entropy extraction is defined as follows.

Assuming that the energy corresponding to $S_{a j}^{i}$ $(i = 0,1, 2, \dots, b)$ is $e$ $(j = 0,1, 2, \dots, b)$ , then:

9

{E_{a j}}^{i} = \int {‖S_{a j}^{i} (t)‖}^{2} d t .

Then the total energy of the signal is:

10

E^{i} = \sum_{j = 0}^{b} E_{a j}^{i},

then the entropy is:

11

H = - \sum_{i = 1}^{b} p (E_{a j}^{i}) l g p (E_{a j}^{i}) .

According to the information entropy, the fuzzy entropy in the frequency domain, the sample entropy, the IMF entropy of the EMD components in the time-frequency domain, and the wavelet packet entropy are obtained. Furthermore, the 32 feature extraction values are used as elements to construct a normalized feature vector as follows:

12

T^{i} = [{f_{a 0}}^{i}, {f_{a 1}}^{i}, \dots, {f_{a b}}^{i}], f_{a j}^{i} = \frac{E_{a j}^{i}}{E^{i}}, (i = 1,2, \dots, k, k + 1, \dots, w, j = 1,2, \dots, b) .

According to the corresponding state of the bearing, the paper designs the state score table of the bearing, as shown in the Table 1 and obtains the corresponding state score matrix $B$ .

As shown in the Table 2, the maximum value of the corresponding state for the training data $S^{1}, S^{2}, \dots, S^{w}$ is 1 and the given state is recorded as the minimum value $ε$ ( $ε$ is a number infinitely close to 0), and for the test data $S^{k + 1}, \dots, S^{w}$ , the score of the state $Z_{v}$ is unknown, given a value of 0, and recorded as $R_{i'}^{j} (i' = k + 1, k + 2, \dots, w, j = 1,2, \dots, v)$ .

Table 1Bearing characteristic score table

Feature	Dataset
Feature	$S^{1}$	$S^{2}$	…	$S^{k}$	$S^{k + 1}$	…	$S^{w}$
${f_{a 0}}^{i}$	${f_{a 0}}^{1}$	${f_{a 0}}^{2}$	…	${f_{a 0}}^{k}$	${f_{a 0}}^{k + 1}$	…	${f_{a 0}}^{w}$
${f_{a 1}}^{i}$	${f_{a 1}}^{1}$	${f_{a 1}}^{2}$	…	${f_{a 1}}^{k}$	${f_{a 1}}^{k + 1}$	…	${f_{a 1}}^{w}$
${f_{a 2}}^{i}$	${f_{a 2}}^{1}$	${f_{a 2}}^{2}$	…	${f_{a 2}}^{k}$	${f_{a 2}}^{k + 1}$	…	${f_{a 2}}^{w}$
$⋮$	$⋮$	$⋮$	$⋱$	$⋮$	$⋮$	$⋱$	$⋮$
${f_{a b}}^{i}$	${f_{a b}}^{1}$	${f_{a b}}^{2}$	…	${f_{a b}}^{k}$	${f_{a b}}^{k + 1}$	…	${f_{a b}}^{w}$

Table 2Bearing condition score table

Bearing status	$S^{1}$	$S^{2}$	…	$S^{k}$	$S^{k + 1}$	…	$S^{w}$
$Z_{1}$	1	$ε$	…	$ε$	$R_{1}^{k + 1}$	…	$R_{1}^{w}$
$Z_{2}$	$ε$	1	…	$ε$	$R_{2}^{k + 1}$	…	$R_{2}^{w}$
$⋮$	$⋮$	$⋮$	$⋱$	$⋮$	$⋮$	$⋱$	$⋮$
$Z_{v}$	$ε$	$ε$	…	1	$R_{v}^{k + 1}$	…	$R_{v}^{w}$

This paper combines the bearing feature scoring matrix $A$ and the bearing status scoring matrix $B$ to obtain a joint scoring matrix $C$ for bearing status recognition; in order to diagnose the state of the test data, we need to decompose the joint scoring matrix $C$ into two low-dimensional feature matrices $P$ and $Q$ , it is $C = P * Q^{T}$ . Furthermore, the state score of the test data is predict $P_{i'}^{j}$ $(i' = k + 1, k + 2, \dots, w; j = 1,2, \dots, v)$ based on these two feature matrices. Finally, the gradient descent method is used to find the optimal parameters $P$ and $Q$ to minimize the overall loss function, and then the test data $S^{k + 1}$ predicts the score $R_{i'}^{j} (i' = k + 1, k + 2, \dots, w; j = 1,2, \dots, v)$ for the state $Z_{j}$ , where $R_{i'}^{j} = P_{i'}^{j} * Q_{i'}^{j}$ , then the state $Z_{j}$ corresponding to the highest score $R_{i'}^{j}$ is the predicted test data state $S^{k + 1}$ .

4. Example verification of different failure forms of bearing outer ring

In order to further verify the effectiveness of the fault identification method proposed in this paper, this section identifies different forms of faults on the bearing outer ring. Using the bearing test stand as shown Fig. 3, set the speed to 1200 rpm and the sampling frequency to 16384 Hz. Experiment with 6205EKA deep groove ball bearings. Collect 402 groups outer ring pitting corrosion and 390 groups outer ring cracks (as shown Fig. 2), outer ring current damage (as shown Fig. 1) 85 groups and normal 423 groups total 1300 sets of data samples.

First use ASMOTE to take 423 groups of normal state samples as reference, oversample a few types of shaft current damage samples by 3 times, and finally get 255 groups of shaft current damage samples, and then further equalize the total 1470 groups of samples according to 6:2:2 ratio is randomly divided into a training set (882 groups), a cross-validation set (294 groups) and a test set (294 groups), and a state-of-the-art recognition is performed using a collaborative filtering recommendation system for bearing state recognition.

As can be seen from the Fig. 5, when the regularization coefficients $λ =$ 0.002 and $K =$ 11, the bearing condition score of the test set reached 99.23 %, and when $K =$ 11, $λ$ is 0.0025, 0.003, and 0.0035, the accuracy of the bearing test set of state has reached 98.63 %, 98.98 % and 98.76 %, respectively. The performance of the model on the test set is evaluated, which proves that the model has good generalization ability under this parameter.

Fig. 1Shaft current damage

Fig. 2Crack damage

Fig. 3Test bench

Fig. 4Accuracy identification CFR

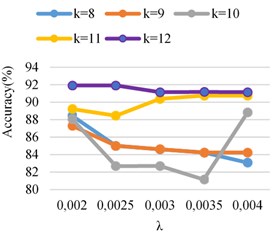
Fig. 5Accuracy identification ASMOTE- CFR

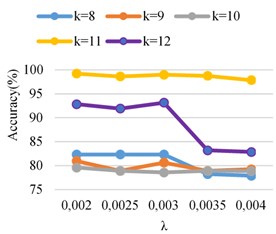
Fig. 6Compare k= 11 the recognition rate CFR and ASMOTE-CFR

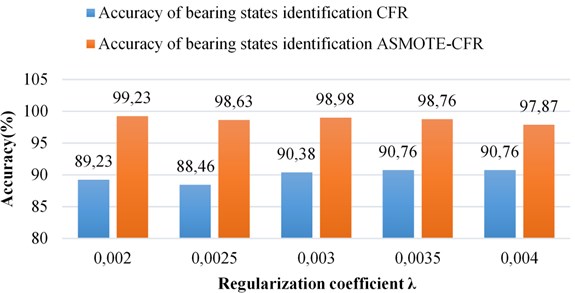
Taking $λ =$ 0.002 and $K =$ 11 as examples, the Table 3 shows the specific recognition of the model for various states on the test set.

Table 3Test set recognition effect

Bearing status	Number of test samples	Recognize the number correctly	Recognize the number false	State recognition accuracy
Crack	69	67	2	97 %
Putting	79	79	0	100 %
Shaft current	49	49	0	100 %
Normal	97	49	0	100 %
Total	294	292	2	99 %

5. Conclusions

In this paper, the combination of adaptive synthetic minority oversampling technology (ASMOTE) and matrix decomposition-based collaborative filtering technology (CFR) is applied to the field of mechanical equipment fault recognition. For the identification of rolling bearing states, this paper oversamples a few types of shaft current samples by three times, then extracts 32 typical features in time domain, frequency domain, time frequency domain and other multi-domain states to construct a bearing feature matrix, and then designs an accurate description of the bearing status , And finally combine these two matrices with different characteristics organically to obtain a joint scoring matrix for bearing status identification. Experiments with different regularization coefficients and eigenvalues on bearings with pitting corrosion, cracks, and current damage on the outer ring of rolling bearings and normal bearings, the highest accuracy rate reached more than 98 %. Compared with CFR, the accuracy of method ASMOTE-CFR is improved by 8 %.

References

Manlangit S., Azam S., Shanmugam B., et al. An efficient method for detecting fraudulent transactions using classification algorithms on an anonymized credit card data set. Proceedings of International Conference on Intelligent Systems Design and Applications, 2017.

Publisher
Liu C., Wu J., Mirador L., et al. Classifying DNA methylation imbalance data in cancer risk prediction using Smote and Tomek Lonk methods. Communications in Computer and Information Science, Vol. 902, Issue 5, 2018, p. 1-9.

Publisher
Al-Azani S., El-Alfy E.-S.-M. Using word embeddings and ensemble learning for highly imbalanced data sentiment analysis in short Arabic text. Procedia Computer Science, Vol. 109, Issue 22, 2017, p. 359-366.

Publisher
Ebo Bennin K., Keung J., Phannachitta P., et al. MAHAKIL: diversity based oversampling approach to alleviate the class imbalance issue in software defect prediction. IEEE Transactions on Software Engineering, Vol. 44, Issue 1, 2017, p. 534-550.

Publisher
Saez J. A., Luengo J., Stefanowski J., Herrera F. SMOTE-IPF: Addressing the noisy and borderline examples problem in imbalanced classification by a re-sampling method with filtering. Information Sciences, Vol. 291, Issue 10, 2015, p. 184-203.

Publisher
Guo Gui Bing, Zhang Jie, Thalmann Daniel, et al. From ratings to trust: an empirical study of implicit trust in recommender systems. Proceedings of the 29th Annual ACM Symposium on Applied Computing, 2014.

Publisher
Kim MinGun, Kim Kyoungjae Recommender systems using SVD with social network information. Journal of Intelligence and Information Systems, Vol. 2, Issue 4, 2016, p. 1-18.

Publisher
Parham Moradi, Sajad Ahmadian A reliability-based recommendation method to improve trust-aware recommender systems. Expert Systems with Applications, Vol. 42, Issue 21, 2015, p. 7386-7398.

Publisher
Ma Hao, Yang Hai Xuan, Lyu Michael R., et al. So Rec: social recommendation using probabilistic matrix factorization. Proceedings of the17th ACM Conference on Information and Knowledge Management, 2008.

Publisher
Rodriguez T., Di Persia L. E., Milone D. H., et al. Extreme learning machine prediction under high class imbalance in bioinformatics. Latin American Computer Conference, 2017.

Publisher
Moreo A., Esuli A., Sebastiani F. Distributional random oversampling for imbalanced text classification. Proceedings of the 39th International ACM SIGIR Conference on Research and Development in Information, 2016.

Publisher

About this article

Received

09 June 2020

Accepted

16 June 2020

Published

29 June 2020

SUBJECTS

Fault diagnosis based on vibration signal analysis

DOI

https://doi.org/10.21595/vp.2020.21520

Keywords

smote

unbalanced data

collaborative filtering

recommended system

Acknowledgements

Financial support from National Natural Science Foundation of China (51575178), financial support from Hunan Natural Science Foundation of China (2018JJ2120) and Hunan Power Machinery Research Institute of AECC.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2024 01 21

Rolling bearing fault diagnosis based on variational mode decomposition and weighted multidimensional feature entropy fusion

Na Lei, Feihu Huang, Chunhui Li

Review article

2023 11 04

A comprehensive review of mechanical fault diagnosis methods based on convolutional neural network

Junjian Hou, Xikang Lu, Yudong Zhong, Wenbin He, Dengfeng Zhao, Fang Zhou

Research article

2023 09 08

Electro-erosion fault identification of motor bearing based on ASMOTE-CFR

Huan Ke Cheng

Review article

2021 11 26

Fault diagnosis and health management of bearings in rotating equipment based on vibration analysis – a review

Adnan Althubaiti, Faris Elasha, Joao Amaral Teixeira

H. Cheng, P. Wang, G. Wang, and Y. Lv, “Bearing fault identification based on ASMOTE-CFR,” Vibroengineering PROCEDIA, Vol. 32, pp. 62–68, Jun. 2020, https://doi.org/10.21595/vp.2020.21520

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2020.21520
UR  - https://doi.org/10.21595/vp.2020.21520
TI  - Bearing fault identification based on ASMOTE-CFR
T2  - Vibroengineering PROCEDIA
AU  - Wang, Guangbin
AU  - Cheng, Huanke
AU  - Wang, Ping
AU  - Lv, Ying
PY  - 2020
DA  - 2020/06/29
PB  - JVE International Ltd.
SP  - 62-68
VL  - 32
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Wang_2020,
	doi = {10.21595/vp.2020.21520},
	url = {https://doi.org/10.21595/vp.2020.21520},
	year = 2020,
	month = {jun},
	publisher = {{JVE} International Ltd.},
	volume = {32},
	pages = {62--68},
	author = {Guangbin Wang and Huanke Cheng and Ping Wang and Ying Lv},
	title = {Bearing fault identification based on {ASMOTE}-{CFR}},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]G. Wang, H. Cheng, P. Wang, and Y. Lv, “Bearing fault identification based on ASMOTE-CFR,” Vibroengineering PROCEDIA, vol. 32, pp. 62–68, Jun. 2020, doi: 10.21595/vp.2020.21520.

Copy IEEE

Copied to clipboard!

Wang, Guangbin, Huanke Cheng, Ping Wang, and Ying Lv. “Bearing Fault Identification Based on ASMOTE-CFR.” Vibroengineering PROCEDIA 32 (June 29, 2020): 62–68. https://doi.org/10.21595/vp.2020.21520.

Copy Chicago

Copied to clipboard!

Bearing fault identification based on ASMOTE-CFR

Abstract

1. Introduction

2. CFR system based on ASMOTE

2.1. Adaptive smote oversampling method (ASMOTE)

2.2. Collaborative filtering recommendation algorithm based on matrix decomposition

3. Bearing fault identification based on ASMOTE-CFR

4. Example verification of different failure forms of bearing outer ring

5. Conclusions

References

About this article

Related Articles