Lyapunov approach and global stability of Ebola virus infection model of an individual cells population

1. Introduction

The virus is known to cause damage to large variety of cell types including monocytes, macrophages, dendritic cells, endothelial cells, fibroblasts, hepatocytes, and several types of epithelial cells. The primary targets of the virus are dendritic, monocytes and macrophage cells [1]. Meanwhile, macrophages are found in many organs such as; lungs, brain, liver, and kidney [1, 3]. The dendritic cells alert the body for any foreign antigen and also serve as potent Antigen Presenting Cells (APC) that capture foreign antigen for uptake and processing to target secondary lymphoid tissues for the simulation of T-cell and B-cells [4]. Macrophages are susceptible to the virus [3], macrophages encounter APC and release a protein called interlenkin-1 (IL-1) that acts as a chemical alarm signal; Helper T-cells respond to interlekin-1 and release interlenkin-2 (IL-2) by simultaneously initiating two parallel lines of immune system defense: the cell-mediated response carried out by T-cells, and humoral response carried out by B-cells [5].

The incubation period of Ebola virus ranges from 2 to 21 days and infectious period ranges from 4 to 10 days [6]. Meanwhile, it takes an approximation of 31 days to quarantine a patient under investigation of the Ebola virus. Consequently, the symptoms of the Ebola virus are characterized by headaches, fever, vomiting, bleeding diarrhoea, and rash [7] in infected person, severe bleeding and shock are usually followed by death [1]. The spread of the virus and eventual death of infected patients was largely contained (reduced) through early detection and effective contact tracing [8]. More so, Mathematical models have played an essential role to study the dynamics of infectious disease [9]. The aim of this paper is to analysis Lyapunov function and global stability of Ebola virus infection model.

2. Model description

The model equations are formulated using ordinary differential equations. We extend the work of [10] by incorporating double immune response, booster parameters and effectiveness of drug administration. $U\left(t\right)$ represents the number of individual cell not yet infected with Ebola virus at time $t$. $I\left(t\right)$ denotes the number of individual cell who have being infected with the Ebola virus and it is capable of producing more viruses and spreading it to uninfected cells. $V\left(t\right)$ is the compartment for free virus being produced from the infected cells. $T\left(t\right)$ is the class denotes the number of cytotoxic T-lymphocyte that destroy infected cells. $B\left(t\right)$ is the antibody immunity that neutralized the free virus in the cell population. The transfer rates between the sub-classes are collection of several epidemiological parameters. The uninfected cell population increase by production rate $\beta$ and having death rate ${\mu }_1$. When a free virus infect the $U\left(t\right)$ population and produced infected cells at rate $\alpha$ and with death rate ${\mu }_2$. Infected cells move to free virus class at rate $\omega$ and free virus die at rate ${\mu }_3$. $T\left(t\right)$ population increase at rate $\gamma$, kill infected cells at rate ${\delta }_1$ and die at rate ${\mu }_4$. $B\left(t\right)$ class produced at rate $\theta$, neutralized the free virus at rate ${\delta }_2$ and ${\mu }_5$ is the death rate of $B\left(t\right)$. We let $\varphi$ be a measure of the effectiveness of the drug in blocking production of infected cells, this affect the dynamics of infected cells directly and viruses indirectly. The effect of $\varphi$ is to reduce the production of infected cells, meanwhile, the range of effectiveness of drug usage is $0\le \varphi \le 1$. Then if $\varphi =1$ it is completely effective and prevents all production of infected cells, while $\varphi =0$ it implies that there is no drug and control intervention against the Ebola virus infection, the booster rates for both $T\left(t\right)$ and $B\left(t\right)$ are $k_1$ and $k_2$ respectively.

Fig. 1Schematic diagram of Ebola virus model with effectiveness of drug usage

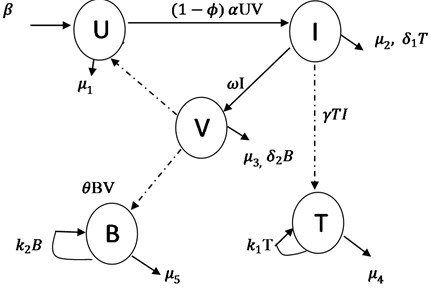
Based on the above schematic representation and assumptions of the models, the equations governing the dynamics of the Ebola virus in human cell population are given as:

3. Equilibrium state of the model equations

At equilibrium state, we let:

This implies:

Solution of Eq. (9) is setting as:

Substitution of Eq. (12) into Eq. (8) is given by:

Or:

Substitution of Eq. (13) into Eq. (12) is given by:

Substitution of Eq. (15) into Eq. (7) is given by:

Eq. (10) yields:

Or:

Eq. (11) yields:

Or:

Therefore, virus free equilibrium (VFE) denoted as:

4. Effective reproductive number, ${\mathit{R}}_{\mathit{e}}$

To derive the effective reproductive number of model (1-5), we first introduce the method of next generation matrix formulated by [11]. Assume the population is divided into n compartments with $m<n$, infected compartments. Let $x=(x_1,x_2,...,x_n{)}^T$, where $x_i\left(t\right)$, $i=\mathrm{1,2},...,m<n$ is the number of individuals in the $i$th infected compartment at time $t$. Both $\mathcal{F}\left(x\right)$ and $\mathcal{V}\left(x\right)$ are obtained from the model Eq. (1-5) of the virus free equilibrium (VFE). Therefore, we have the following:

The characteristics equation of Eq. (24) is setting as:

Determinant of Eq. (25) yields:

$R_e$ is the largest eigenvalue which is spectral radius of $e\left(F{V}^{-1}\right)$. Therefore, the effective reproductive number is given by:

The Eq. (27) is the effective reproductive number of the system Eqs. (1-5).

5. Global stability of virus free equilibrium (${\mathit{E}}^0)$

We used Lyapunov function to investigate the stability of the virus free equilibrium,

Theorem 1: The Virus Free Equilibrium, $E^0$ of Eqs. (1-5) is globally asymptotically stable (GAS) if ${\mathit{R}}_{\mathit{e}}\le 1$.

Proof: To establish the global stability of the virus free equilibrium, we select the infected classes for construction of Lyapunov function. We have:

as a good candidate for a Lyapunov function and must satisfied:

We take derivative of Eq. (28) yields:

We substitute Eq. (2) and Eq. (3) into Eq. (30) and get:

Eq. (31) reduced to:

At the virus-free equilibrium state, Eq. (32) yields:

From Eq. (33), we have:

Hence, yields

The virus-free equilibrium is globally asymptotically stable (GAS) if $R_e\le 1$.

6. Virus persistence equilibrium (VPE)

Let:

From Eq. (36), Eqs. (1-5) becomes:

Substitute Eq. (20) into Eq. (37) and we have:

Substitute Eqs. (18), (20) and (42) into Eq. (38) and we have:

Substitute Eqs. (18) and (20) into Eq. (39), we get:

Therefore, virus persistence equilibrium (VPE) denoted as:

7. Global stability of virus persistence equilibrium, ${\mathit{E}}_1$

Theorem 2: The VPE of the model equations is globally asymptotically stable (GAS) if $R_e\ge 1$.

Proof:

The Lyapunov function $L=(U,I,V,T,B)$ is defined as:

The differentiation of Eq. (46) yields:

Eq. (47) yields:

At endemic states, we let:

Substitute Eqs. (49-53) into Eq. (48), we get:

Implies:

Eq. (55) yields:

Implies:

where:

From Eq. (57) if $M<N$ then $dL/dt$ will be negative definite meaning that $dL/dt<0$, it follows that $dL/dt=0$ if and only if $U=U^{\mathrm{*}}$, $I=I^{\mathrm{*}}$, $V=V^{\mathrm{*}}$, $T=T^{\mathrm{*}}$, $B=B^{\mathrm{*}}$. Therefore, the largest compact invariant set in $\left\{U^{\mathrm{*}},\right.I^{\mathrm{*}},V^{\mathrm{*}},T^{\mathrm{*}},B^{\mathrm{*}})\in {\mathfrak{R}}^5:dL/dt=\left.0\right\}$ is the singleton $\left\{E_1\right\}$ where $E_1$ is the virus persistence equilibrium of the model Eqs. (1-5). By Lasalle’s invariant principle, it implies that $E_1$ is globally stable in ${\mathfrak{R}}^5$ if $M<N$. Otherwise, it is unstable if $M>N$. This completes the proof of Theorem 2.

8. Conclusions

In this paper, we analysed Lyaponuv function and global stability of a mathematical model of Ebola virus infection, a mathematical model for the dynamics of Ebola virus infectious of an individual was presented. The virus free equilibrium (VFE), virus persistence equilibrium (VPE) and effective reproduction number of the model were obtained. The conditions under which the virus-free-equilibrium was globally asymptotically stable with method of linear Lyapunov function were shown when the effective reproduction numbers less than unity. The nonlinear Lyapunov function of global stability of the virus persistence equilibrium was shown and we found that VPE is globally asymptotically stable if $M<N$, otherwise unstable if $M>N$.