Fast calculation method of directly buried cables ampacity

1. Introduction

The calculation methods of cable ampacity can be divided into analytical method and numerical method, the former refers to the IEC-60287 standard recommended by the International Electrotechnical Commission [1], the equivalent thermal circuit method provided by this standard has a fast calculation speed, but the calculation error is larger in the non-uniform soil environment containing backfill soil with poor thermal conductivity; the latter calculation of the cable ampacity is based on the calculation of the temperature field, with high accuracy but slower speed. Common methods mainly include: finite element method [2-4], boundary element method [5], finite difference method [6, 7] and simulated heat charge method [8].

Compared with the entire laying area, the cable body occupies a very small space, the effect on computation speed is negligible. The calculation time required by the numerical method is mostly used to calculate the temperature field of the laying area outside the cable body [9, 10]. The reason why the high calculation efficiency of the equivalent thermal circuit method is due to this method can quickly calculate the external thermal resistance of cables [11, 12]. When the laying environment is uniform soil (single thermal conductivity), the calculation accuracy of the equivalent thermal circuit method for the external thermal resistance of the cable is very high, which has a very good application effect. When the laying environment is non-uniform soil (the thermal conductivity is not single), the equivalent thermal circuit method needs to adopt the correction coefficient to correct the cable external thermal resistance, its correction error increases with the increase in the number of cable circuit and the thermal resistance coefficient of the backfilled soil [13], which makes the application of the equivalent thermal circuit method have strong limitations, in this case numerical methods used to solve the cable ampacity problem [14].

If the external thermal resistance of cables under complex laying environments can be accurately calculated, it will greatly expand the application space of equivalent thermal circuit method. In this paper, combining the advantages of the equivalent thermal circuit method and the numerical method, new method for calculating the ampacity of the cable group is proposed. Without considering cable external thermal resistance in a certain temperature range changes with temperature changes, first a round of numerical iteration is adopted to obtain the steady-state temperature field of the cable group under a certain load current. The soil temperature and cable core temperature in the laying area are substituted into the equivalent thermal circuit formula to solve the external thermal resistance of cables. On this basis, the equivalent thermal circuit method can be adopted to accurately calculate the ampacity of the cable group. The method does not need to use correction coefficients, so it can avoid the calculation errors caused by the correction process. At the same time, the equivalent thermal circuit method is used multiple times to replace the repetitive iteration in the numerical calculation, which greatly improves the calculation efficiency. The new method proposed in this paper is faster than the pure numerical method, and which is more accurate than the analytical algorithm.

2. Analytical method for calculating cable ampacity

According to the principle of equivalent thermal circuit, the analytical calculation formula of cable ampacity $I$ is given in IEC standard [1]:

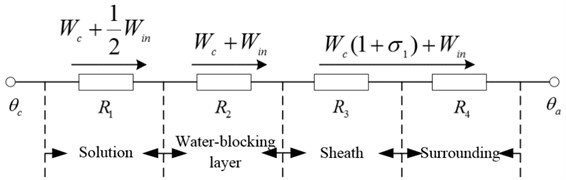
Fig. 1 shows the overall equivalent thermal circuit of the cable when the outer part of the cable core is composed of an insulating layer, a water blocking layer and an outer sheath in turn. In Eq. (1), ${\theta }_{max}$ is the maximum allowable long-term operating temperature of cable core; $R$ is the AC resistance per unit length when the cable core temperature is ${\theta }_{max}$, Ω; $n$ is the number of conductors, and single-core cable $n=$ 1. In the Fig. 1, $R_2$, $R_3$, $R_4$ are the thermal resistance of the water blocking layer, the thermal resistance of the outer sheath and the surrounding medium (external) thermal resistance, $W_c$ and $W_{in}$ are the cable core and insulation loss (W), and ${\lambda }_1$ is the metal sheath loss coefficient, ${\theta }_a$ is the temperature of the medium around the cable.

Fig. 1All of the equivalent thermal roads of cable

If a total of $M$ cables are laid, the buried depth of a certain cable is $L$, and the thermal resistance coefficient of the soil adjacent to the cable group is ${\rho }_{T4}$, then the $R_4$ of the cable is [15]:

In Eq. (2), $M$ is the number of cables, $d_{1K}$, $d_{2K}$,..., $d_{MK}$ are the distance from the center of the cable 1, 2,..., $M$ to the center of the cable; $d_{1K}^{\mathrm{\text{'}}}$, $d_{2K}^{\mathrm{\text{'}}}$,..., $d_{MK}^{\mathrm{\text{'}}}$ are the cable 1 respectively, 2… the distance from the center of the mirror image of $M$ to the center of the $K$ cable, $D_{ou}$ is the outer diameter of the cable sheath (m). It should be noted that $d_{KK}^{\mathrm{\text{'}}}/d_{KK}$ is not included. If the thermal conductivity of the soil in the radiation area is not unique, reference [15] adopts a modified method to calculate the external thermal resistance of the cable:

In Eq. (3),$R_e=\left(N/2\pi \right)\left({\rho }_e-\rho \right)\ln \left(u+\sqrt{u^2-1}\right)$, $u=L_G/r_b$,$L_G$ is the depth from the ground to the center of the backfill, $r_b$ is the equivalent radius of the backfill. If $x$ and $y$ are used to represent the length and width of the backfill area, $r_b$ can be expressed as: $\mathrm{l}\mathrm{n}{r}_b=\left(x/2y\right)\left(4/\pi -x/y\right)\ln \left(1+x^2/y^2\right)+\mathrm{l}\mathrm{n}\left(x/2\right)$, ${\rho }_e$ and $\rho$ are the thermal resistance coefficients of soil and backfill which is cement precast parts, K·m/W.

Calculations by previous researchers have shown that when the laying environment is non-uniform soil, the calculation error caused by the above correction method to calculate the external thermal resistance coefficient of the cable will increase with the increase of the backfill soil and the number of cable circuits. Therefore, this method has great limitations in dealing with the ampacity of the cable group in a complex laying environment.

3. The new method proposed in this article

In this paper, combining the advantages of the equivalent thermal circuit method and numerical calculation method, a new method for calculating the ampacity of the cable group is proposed. The implementation process of this method is as follows.

(1) Given a load current value $I_0$, adopt the numerical method of literature [13] to calculate the steady-state temperature field of the cable group corresponding to the current value.

(2) Take several concentric “soil layers” with equal thickness on the outside of the cable, and calculate its thermal resistance as$R_T=\frac{{\rho }_{T4}}{2\pi }ln\frac{(D_{ou}+2d)}{D_{ou}}$ ($d$ is the total thickness of soil layer).

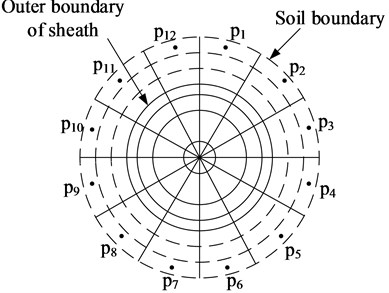
(3) As shown in Fig. 2, calculate the average temperature ${\theta }_p$ [16] of the outermost soil layer using the quadratic interpolation method.

(4) Replace ${\theta }_a$ and $R_4$ in Eq. (2) with ${\theta }_p$ and $R_T$ respectively, and calculate the cable core temperature ${\theta }_c$.

(5) Substitute the calculated steady-state temperature ${\theta }_{ci}$ of each cable core and the mother soil temperature ${\theta }_a$ of the cable laying area into Eq. (2) again, and calculate the corresponding external thermal resistance $R_{4i}$ of each cable under this working condition.

(6) Substitute the obtained external thermal resistance $R_{4i}$ of each cable into Eq. (4), calculate the maximum long-term operating current allowed by each cable, and select the minimum value as the ampacity of the cable group.

Fig. 2Temperature of the soil near the cable

Compared with the two numerical methods in references [14] and references [16], the new method proposed in this paper has the biggest advantage is that when calculating the ampacity, only one calculation of steady-state temperature field under rectangular coordinates is required, and the rest of the calculation process is completed by analytical algorithm, which can significantly improve the calculation efficiency on the premise of ensuring the calculation accuracy. Although the calculation time of this method is increased compared with the analytical algorithm, it can realize the accurate calculation of the external thermal resistance of the cable under the complicated laying environment such as different backfilling methods, avoiding the calculation error caused by the correction method, and greatly expands the application space of Eq. (1).

4. Ampacity calculation and method verification

In order to verify the accuracy and efficiency of the new method in this paper, calculate the ampacity of 66 kV single-circuit and double-circuit XLPE insulated power cables under two working conditions of uniform soil and back filled sand soil. The cable is made of copper core, and the length is 800 m, and the aluminum sheath is grounded by cross interconnection method. The nominal cross section is 630 mm², the soil ambient temperature is 25℃ when the uniform soil is laid, and the soil thermal resistance coefficient is 1.2 K∙m/W. What’s more, the laying method of backfill sand soil is shown in Fig. 3 and the thermal resistance coefficient of sand soil is 3.33 K∙m/W.

Fig. 3The laying-manners of 66 kV cable with single and double circuits when backfilling sand soil

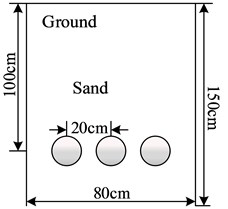
a) Single circuit laying

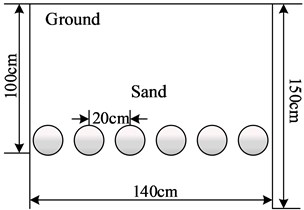
b) Double circuit laying

Table 1 shows the case of laying and backfilling sand soil in uniform soil, the analytical method, coordinate combination method, field-circuit combination method and the new method are used to calculate the results of the cable ampacity under the above working conditions. Since the analytical method can accurately calculate the ampacity of cable in uniform soil, it can be used as a standard to verify the accuracy of other methods. In Table 1, $I_1$ and $I_2$ are the ampacity of single, double-circuit cables respectively, and $t_1$ and $t_2$ are the calculation time of single, double-circuit cable current-carrying capacity respectively.

As can be seen from Table 1, coordinate combination method [14], field circuit combination method [16] and the new method in this paper all agree well with the analytical method when calculating the ampacity of cables laid in uniform soil, which proves the accuracy of the new method in this paper. When the laying area is backfilled with sand soil, the calculation results of the new method in this paper are in good agreement with the calculation results of the coordinate combination method and the field circuit combination method, but the calculation time is significantly reduced, which indicates that the new method in this paper can significantly improve the calculation efficiency on the premise of ensuring the calculation accuracy.

5. Conclusions

In this paper, the analytical calculation formula of the cables ampacity provided by IEC standard is improved because of the limitation of its application. The proposed new method realizes the accurate calculation of the external thermal resistance of the cable by calculating the primary steady-state temperature field, and then can accurately calculate the cable group ampacity. This method avoids the use of a correction method to deal with the problem of the current carrying capacity of the cable when there is backfill soil, eliminates the application limitations of the analytical calculation formula. Comparing with the coordinate combination method and field-circuit combination method proposed by researchers before, the new method proposed in this paper has both the high precision of numerical calculation and the high efficiency of analytical calculation, and has high engineering application value.