Abstract
The solution of the problem of cylindrical column on a rigid horizontal foundation motion is presented. It is assumed that the base moves in a horizontal direction, there is no slippage between the column and the base, and the column height is significantly greater than the base diameter. The modes of oscillations of the column, corresponding to the main resonance for two laws of the base motion are found. The results are presented in the form of amplitude-frequency characteristics. It is shown that the solutions corresponding to the column motion in the plane of vibration excitation are unstable.
1. Introduction
The study of the motion of a rigid body on a horizontal supporting surface is of great interest for applications in technology. The problem of vibrations of a rigid body in the form of a parallelepiped on a vibrating base was first considered in [1]. In this and a number of other works [2-4], this problem was considered in relation to the problems of seismic stability. There are other technical areas of application of this problem, for example, the problem of the movement of parts on a conveyor. The exact solution to the problem of vibrations of a parallelepiped on a vibrating base was obtained in [5], and in [6, 7] the averaging method was used, which made it possible to investigate the stability of the solutions obtained. A detailed list of publications on the issue of seismic stability of elongated structures is given in [8].
In his article in 1963, G. Housner [1], analyzing reports on a number of earthquakes, drew attention to the fact that structures that are highly elongated in height can safely withstand earthquakes, despite their unstable appearance. The explanation for this phenomenon lies in the existence of stable vibration modes, in which the body consistently rests on the ribs of the base. In this work and a large number of subsequent ones, a body in the form of a parallelepiped was considered as a model, although most of the structures (water tanks, stone columns) have a base in the form of a circle.
In this paper, the dynamics of similar systems, but with a base in the form of a circle, is investigated.
2. Formulation of the problem
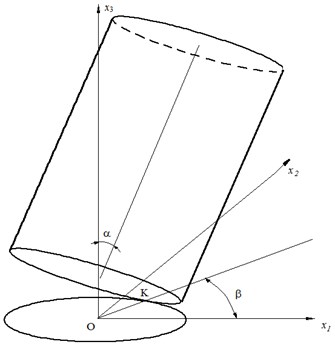
Consider the motion of a rigid body in the form of a column with circular cross-section on a horizontal supporting surface, performing harmonic oscillations in the horizontal direction. A rigid body on a support surface in the absence of slippage is a system with two degrees of freedom. In the equilibrium position, the central axis of the column coincides with the normal to the supporting plane, and the bottom base rests completely on the plane. When motions, the axis of the column deviates from the vertical by a certain angle (Fig. 1). We assume that there is no slippage at the point of contact between the column and the plane, and, in addition, the column cannot rotate about the vertical axis. This formulation of the problem corresponds to the case of taking into account the forces of interaction between the base and the column according to the Coulomb friction model, with a finite area of the contact patch and a sufficiently large value of the friction coefficient.
We will also assume that the column is strongly elongated in the vertical direction and the ratio of the base radius to the half-height of the column is small.
We take , – the angles of rotation of the column axis relative to the axes , associated with the movable base as a generalized coordinates. From the last assumption , and we can put . The kinetic energy of the system is. For a column extended in height, we put
Fig. 1The design scheme
The potential energy of the system , where is the mass, is the gravitational acceleration, is the angle between the axis of the column and the line connecting the center of mass of the column C with the point contact. Generalized forces:
where is the vibration frequency of the supporting surface, , , are the amplitudes and phase of the base motions in two orthogonal directions.
Substituting the obtained formulas into the Lagrange equations of the second kind, we obtain the equations of motion of the system:
where, the dimensionless time is introduced, where , the dimensionless amplitude and frequency of oscillation excitation are , , . The dot denotes the derivative with respect to the dimensionless time. Dissipation according to the model of viscous friction with a dimensionless friction parameter is introduced into the equations of motion.
The system of Eq. (1) describes the motion of a strongly nonlinear system. With and , we obtain the equation of column vibrations on a fixed plane, which has two solutions. The first solution corresponds to the vibrations of the column in the plane located at an angle to the axis. For one oscillation period, this solution has the form [6]:
where , are the amplitude and frequency of natural vibrations, interconnected by the dependence:
If Eqs. (1) coincide with the equation of vibrations of a rigid body in the form of a parallelepiped on a vibrating base. The generating solution in this case coincides with Eq. (2) for . Unlike a rigid body in the form of a parallelepiped, a cylindrical column can vibrate freely in any plane. The solution obtained in [6] by the averaging method describes the vibrations of a cylindrical column in the plane of excitation of vibrations, however, it requires an additional study of stability. The second solution describes motion in space:
In this case, the base of the column rolls in a circle with center on the reference plane (Fig. 1). After substituting Eq. (4) into Eq. (1), we obtain the dependence of the oscillation amplitude on frequency for this solution:
Let us change the variables in Eq. (1):
where is the angle of deviation of the column axis from the vertical, is the angle formed by the radius vector OK of the contact point with the axis. Let us introduce the notation – the angular velocity of the column relative to the axis perpendicular to and – the angular velocity of the contact point along a circle with center on the reference plane. The equations for the vibrations of the column in the new variables have the form:
Next, we consider the problem of forced vibrations of a column on a moving base in the vicinity of the generating solution Eq. (4). In new variables, this solution , , and are constants related by relation Eq. (5). We restrict ourselves to solving the system of Eq. (6) for two types of base motion.
3. Base motion in a circle
Consider the special case , , which corresponds to the motion of all points of the supporting plane along a circle. For steady-state forced vibrations, there is an exact solution to the problem. Setting , we obtain a system of equations that does not explicitly contain time on the right-hand side:
The solution of the system Eq. (7) is:
In this case, the column has a constant angle of deviation from the vertical, and the point of contact moves in a circle with a constant angular velocity equal to the angular velocity of movement of the base. The last two formulas Eq. (8) are amplitude-frequency and phase-frequency characteristics, respectively. To study the stability of the obtained solution, we consider a matrix consisting of partial derivatives of Eqs. (7) with respect to , , and . After substituting , from solution Eq. (8), this matrix has the form:
The asymptotic stability was investigated using the Routh-Hurwitz criterion.
Fig. 2Amplitude-frequency characteristic
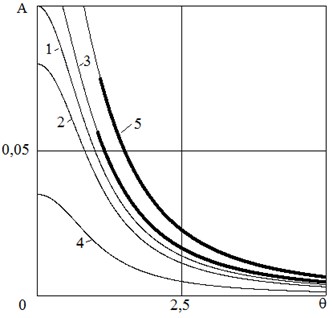
Fig. 3Phase-frequency characteristic
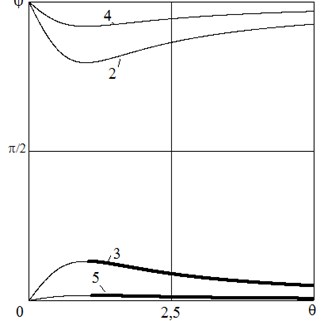
Dependences and are shown in Figs. 2 and 3 with the ratio of the base radius to the column half-height 0.1, the friction coefficient 0.1. Curves 2, 3 correspond to the amplitude of acceleration of the base 0.02, curves 4,5 – 0.065. Bold lines indicate stable solutions. Dependences are adjacent to curve 1 – the dependence of the amplitude on the frequency of free vibrations Eqs. (5). Curves 2 and 4 are located below curve 1 and correspond to unstable solutions with the phase . Dependences 3 and 5 have a stable and unstable section, the border between them shifts to the right with an increasing of the excitation amplitude.
4. Base motion along a straight line
Consider one more special case , in which all points of the support plane move along a straight line. As in the previous case, we put. The system of equations has the form:
The system of differential Eq. (9) explicitly contains the fast variable on the right-hand side. We will use the averaging method [9, 10], for which we assume that the value of the viscous friction coefficient , the excitation amplitude , the angular velocity and the frequency detuning are small. In the vicinity of the generating solution, the term in the first equation is small. The functions are slow variables of the dimensionless time . Applying the averaging procedure and keeping the previous notation for the averaged variables, we obtain:
For steady-state oscillations, we assume the left-hand side of equations Eq. (10) to be equal to zero. The solution of the resulting system coincides with Eq. (8) taking into account the replacement . The amplitude-frequency and phase-frequency characteristics coincide with those shown in Fig. 2 and 3, curves 2, 3 correspond to 0.04, curves 4.5 - 0.13. In contrast to the previous case, for the movement of the base along the straight line and in Fig. 2 and 3 are the averaged values of the amplitude and phase of the oscillations.
There is one more solution corresponding to the movement of the column in the plane of excitation of oscillations. Let us prove that the generating solution Eq. (2) of the system of Eq. (1) is unstable. For free vibrations of a column on a fixed plane without friction, the system of Eqs. (6) has the form:
Consider its solution under the initial conditions , , , . The solution , is periodic with the interval , and on the interval has the form:
has period :
The second equation in Eq. (11) has a solution and system can be written in the form:
The solution corresponding to the motion of the column in the plane is realized only when . When the initial velocity is nonzero, the modulus of the angle increases indefinitely. This means that the motion of a column with a round base in one plane is unstable.
5. Conclusions
At small values of the acceleration amplitude of the base or and zero initial conditions, the column remains in a vertical position, the movement of the base only leads to a redistribution of the pressure of the lower edge of the column to the support plane. Under arbitrary initial conditions, or large amplitudes of excitation, the column can overturn. From the analysis of the results obtained, it follows that at low frequencies of vibration excitation, there are only these two variants of the motion of the system. When the excitation frequency exceeds a certain critical value, the value of which depends on the parameters of the problem, a stable solution exists for the system under consideration (Figs. 2 and 3). In this case, the base of the column rolls in a circle on the reference plane. Thus, even with large amplitudes of base motion, the column may not tip over.
The form of the amplitude-frequency dependences for a column with a round base and a parallelepiped [6] qualitatively coincide, but these are completely different curves adjacent to dependences Eqs. (5) and (3), respectively.
The assumption introduced at the beginning of the article about the absence of slippage at the point of contact of the column with the base reduces the scope of the results obtained. The problem requires additional research for various models of forces and moments of friction at the point of contact.
References
-
Housner G. The behavior or inverted pendulum structures during earthquakes. Bulletin of Seismological Society of America, Vol. 53, Issue 2, 1963, p. 403-417.
-
Hogan S. J. The many steady state responses of a rigid block under harmonic forcing. Earthquake Engineering and Structural Dynamics, Vol. 19, 1990, p. 1057-1071.
-
Sinopoli A. Earthquakes and large block monumental structures. Annali di Geofisica, Vol. 38, Issues 5-6, 1995, p. 737-751.
-
Prieto F., Lourenco P. B. On the rocking behavior of rigid object. Meccanica, Vol. 40, 2005, p. 121-133.
-
Karapetyan A. V., Munitsyna M. A. Dynamics of a parallelepiped on a horizontal vibrating plane. Automation and Remote Control, Vol. 76, Issue 3, 2015, p. 394-404.
-
Munitsyn A. I., Munitsyna M. A. Oscillations of a Rigid Block on Supported Base. Vibroengineering Procedia, Vol. 8, 2016, p. 63-67.
-
Munitsyn A. I., Munitsyna M. A. Oscillations of a Rigid block on supported base with coulomb friction. Problems of Mechanical Engineering and Engineering Education, Vol. 4, 2016, p. 10-16, (in Russian).
-
D’angela D., Magliulo G., Cosenza E. Towards a reliable seismic assessment of rocking components, Engineering Structures, Vol. 230, 2021, p. 111673.
-
Bogolyubov N. N., Mitropolskiy Yu A. Asymptotic Methods in the Theory of Nonlinear Oscillations. Nauka, Moscow, 1974, p. 503, (in Russian).
-
Babitskiy V. I., Krupenin V. L. Oscillations in Highly Nonlinear Systems. Nauka, Moscow, 1985, p. 320, (in Russian).
About this article
This research was financed by the Russian Foundation for Basic Research (19-01-00140) and Program No 29 “Advanced Topics of Robotic Systems” of the Presidium of the Russian Academy of Sciences.
