Discrimination method of low-current grounding fault of primary and secondary integrated equipment under three-phase asymmetric harmonic power flow calculation

1. Introduction

Most of today’s distribution networks are low-current grounding systems, and the detection of grounding faults has always been a technical problem plaguing the operation of distribution networks [1]. In recent years, with the wide application of power electronics technology and the increase of various nonlinear loads, harmonic pollution in power system has become increasingly serious, which has become a public hazard affecting power quality [2]. With the increase of people’s electricity demand, eliminating the risk of accident expansion and further improving the safety and reliability of power supply have been put on the agenda. However, the identification and judgment of small current ground fault of primary and secondary integrated equipment still need to be improved [3]. At present, people generally use the method of single-phase model analysis to calculate the distribution of harmonics, but the accuracy of this method is difficult to meet the actual demand, so it is necessary to study a method that can meet the effective discrimination of small-current ground faults of primary and secondary fusion equipment [4].

Reference [5] proposed a discrimination algorithm for the direction of grounding fault in flexible grounding system based on the change of zero sequence admittance. By analyzing the zero sequence measurement admittance characteristics of the upstream, downstream and sound lines of the fault point before and after the parallel small resistance is put into operation when a single-phase grounding fault occurs in the flexible grounding system. It is found that the zero-sequence measurement admittance of the downstream of the fault point and the sound line before and after the connection of the small parallel resistance is unchanged, and the modulus-to-value ratio is 1, while the modulus-to-value ratio of the zero-sequence measurement admittance of the upstream line of the fault point is much larger than 1. This method is not easy to be affected by line parameters and transition resistance, but its detection accuracy still needs to be improved. Reference [6] proposed a high resistance grounding fault diagnosis method based on the projection difference between the neutral point current and the line zero sequence current. After the grounding fault occurs, the fault line passes through the grounding point and the system neutral point to form a basic zero sequence circuit. Because the neutral point current is resistive, the difference between the projection of the zero sequence current of the fault line on the neutral point current and the neutral point current is small, while the zero sequence current of the non fault line is basically capacitive, and the difference between the projection of the zero sequence current of the non fault line on the neutral point and the neutral point current is large. This method has high sensitivity and reliability, but it is not accurate enough to identify the fault of the docking ground. Reference [7] proposed a method to identify the grounding phase that can adapt to the asymmetry of the system. If only one phase voltage amplitude decreases after the fault compared with that before the fault, this phase is the fault phase; If two-phase voltage amplitude decreases, the lagging phase of the voltage amplitude increasing phase in the neutral ungrounded system is the fault phase, and the leading phase of the voltage amplitude increasing phase in the over compensated state of the resonant grounding system is the fault phase. This method can accurately identify the phase of ground fault under asymmetric conditions, but it is difficult to be applied to other conditions for accurate detection.

On the basis of the above methods, in order to further improve the effect of fault identification, considering the single phase has been difficult to meet the needs of today’s harmonic power flow calculation, and no convergence problem may emerge in the traditional algorithm, based on the asymmetric three-phase harmonic power flow calculation, for a quadratic convergence complete equipment for small current grounding fault. In this paper, the three-phase asymmetric harmonic power flow is calculated first. According to the calculation results, the grounding fault line selection model is built, and then the fault line is obtained; the transient zero-sequence power direction is extracted by wavelet packet transform method, which is used as the line selection criterion to judge whether ground fault occurs; the amplitude characteristic enhancement value of each section is calculated, and the fault section is selected, in which the mutation logic array is used to determine the small current ground fault.

2. Ground fault line selection

3. Ground fault zone location

In order to enhance the amplitude characteristics and facilitate the detection and collection of fault signals, an adjustable zero-sequence current signal is injected into the low-current grounding system through the PWM active inverter device, and the neutral point voltage is continuously regulated, thereby regulating the fault phase voltage. Fig. 1 is a schematic diagram of the structure of the neutral point injection signal.

In Fig. 1, $W_A$, $W_B$ and $W_C$ are the power supply voltages of $A$, $B$ and $C$ phases, $F_A$, $F_B$, $F_C$, $Q_A$, $Q_B$, $Q_C$ are the conductance and capacitance of the three phases to ground, and $I_x$ is the zero injected by the PWM active inverter device. sequence current. Taking $C$ phase reference, when a ground fault occurs in the distribution network shown in Fig. 1, the relationship between the neutral point voltage $U_z$ and the injection current $I_x$ is:

Fig. 1Schematic diagram of the neutral point injection signal structure

Adjust the neutral point voltage $U_z=-W_C$, the fault phase voltage $U_C=0$, to achieve fault arc suppression. The value of the injected zero sequence current $I_x$ should be:

Use the FTU or fault indicator to collect the zero-sequence current signal corresponding to each terminal and upload it to the master station, make a difference between the zero-sequence current of each section during arc suppression and extract the amplitude:

where, $n$ and $m$ represent the adjacent detection points, $n=m+1$; ${\partial }_{\omega }$ represents the scalar sum of the ground admittance.

After a delay of 5 s, the injected zero-sequence current signal is changed, and the neutral point voltage is regulated, so as to regulate the fault phase power supply voltage whose fault phase voltage is $\lambda$ times: $U_C=\lambda W_C$, and $U_0=W_C\left(\lambda -1\right)$ at this time. Through the active detection of the injected signal, it will not depend on the change of the parameters of the asymmetric distribution network before and after the occurrence of the ground fault, eliminate the influence of the false zero-sequence amplitude component generated by the three-phase unbalance, amplify the fault characteristics, and facilitate the collection of the fault steady-state component. with measurement. Considering that the fault phase voltage and neutral point voltage do not exceed $\sqrt{3}$ times the phase voltage, the definition domain of the regulation coefficient $\lambda$ is taken as [0,1]. According to Eq. (15), the corresponding injection current $I_x$ is the injected current signal at this time:

After the fault arc extinguishing delay of 5 s, the primary duration of regulating the zero-sequence current is 50 ms, and the $\lambda$ value is changed to continue regulating after the compensation arc extinguishing is put into operation for 2 s. There is a transient process in the control process, and a short-term inrush current will appear. In the steady state of the fault, the fault characteristics are amplified, the regulation coefficient and regulation range are determined, and the adverse impact on the distribution network is reduced. The standard GB/T 50064-2014 stipulates that the residual current at the fault point of the 6-66 kV distribution network should not exceed 10 A, and the coefficient $\lambda$ for regulating the magnitude of the fault phase voltage after the arc extinguishing delay satisfies:

It can be seen from Eq. (16) that when $R_f\le \left(W_C/10\right)$, the range of the control coefficient $\lambda$ is $\left[\mathrm{0,10}{R}_f/W_C\right]$, where $\left[\mathrm{0,10}{R}_f/W_C\right]\in \left[\mathrm{0,1}\right]$; when $R_f>\left(W_C/10\right)$, the control coefficient can take values in the entire definition domain. The voltage phasor diagram of the regulation process is shown in Fig. 2.

Fig. 2Voltage phasor during regulation process

In Fig. 2, in the process of regulating the voltage, the zero-potential point $O$ moves along the $U_0$-phasor direction. The fault characteristics gradually increase, limit the voltage rise of the non-faulty phase, and reduce the breakdown risk of the weak insulation of the non-faulty phase. At the same time, the amplitude of the fault current is limited, and the inrush current is small. For the healthy section, the difference of the zero-sequence current amplitude is only related to the ground parameters of the section; for the fault section, in addition to the ground parameters, it is also related to the transition resistance value, so the zero-sequence current difference amplitude of each section is:

where, $I_{0p}$ and $I_{0q}$ respectively represent the amplitude components corresponding to the $p$ and $q$ detection points when the control fault phase voltage is ${\lambda }_p$ times the power supply voltage; ${\psi }_o$ represents the control coefficient interval value.

In order to maximize the amplitude feature, the amplitude feature enhancement sequence when the fault feature is amplified to different degrees is constructed for each detection section:

Establish an amplitude accumulation strategy under the magnification feature to evaluate the difference, and superimpose each element in Eq. (20) to obtain the amplitude feature enhancement value of each segment:

where, ${\lambda }_1$ represents the first regulation coefficient. When the transition resistance is small and satisfies $R_f\le \left(W_C/10\right)$, select the initial control coefficient ${\lambda }_0=0$, and the control coefficient interval value ${\alpha }_k=10R_f/W_C$, namely ${\lambda }_1={\alpha }_k$. When the transition resistance is large, the control range is [0, 1] interval, ${\alpha }_k=\text{0.25}$. The amplitude characteristic of the sound section in Eq. (19) shows a decreasing trend. Considering that the maximum amplitude characteristic of the sound section is smaller than the threshold, the Eq. (18) can be substituted, the threshold $\mathrm{\Delta }{I}_g=\left(I_{0p0}-I_{0q0}\right)+\nu$ can be set, and a certain margin $\nu$ can be reserved. According to the engineering site and the accuracy settings of the detection equipment. The amplitude characteristic enhancement value of each section is calculated, and the corresponding section is selected as the fault section according to the distribution characteristics of the zero-sequence current amplitude of the faulted feeder.

4. Method for determining small current grounding fault based on mutation logic array

Since the small current ground fault can cause the current change of the faulted phase upstream of the fault point, the fault point can be determined by analyzing the current change before and after the fault of each feeder.

Definition of feeder real-time current array $H_i$ describes the $A$, $B$ and $C$ three-phase real-time operating states of all switches and distribution transformers of a distribution feeder, and the specific description is as follows:

where, $h_{al}$ represents the real-time current value of phase $A$ of the $l$-th switch or distribution transformer (distribution transformer) included in the feeder; $h_{bl}$ represents the real-time current value of phase $B$ of the $l$-th switch or distribution transformer included in the feeder; $h_{cl}$ represents the real-time current value of phase $C$ of the $l$-th switch or distribution transformer included in the feeder; $l=\mathrm{1,2},...,m$, $m$ represent the total number of switches and distribution transformers included in the feeder.

Definition of feeder history current array $V_j$ describes the $A$, $B$ and $C$ three-phase historical operation states of all switches and distribution transformers of a distribution feeder, and the specific description is as follows:

where, $v_{al}$, $v_{bl}$ and $v_{cl}$ are the historical current values of $A$, $B$ and $C$ phases of the $l$-th switch or distribution transformer included in the feeder, respectively. The historical time can be set according to the terminal type. If it is a high-precision real-time acquisition device with a short equal sampling interval, the historical time can be set to 2-5 min before the current time; if the sampling interval such as a fault indicator and an intelligent distribution transformer terminal is longer if the acquisition device is a collection device, the historical time can be set to 5-10 min before the current time; if the collection device is a mixed configuration of fault indicators, the historical time can be set to 5-10 min before the current time; If it is forwarded by the electrical information collection system, the historical time can be set as 5-10 min before the current time. The purpose of the time setting is to ensure that all data are uploaded to the DMS master station. When a ground fault occurs, the real-time current array of the feeder after the fault and the historical current array of the feeder before the fault can be used to calculate the steady-state current change caused by the fault. The specific description is:

where, $ACM$ represents the sudden change current matrix of the feeder, which is a $3\times m$ matrix. For the convenience of calculation, the sudden change of feeder current is expressed by the feeder mutation logic matrix $ASM$:

Among them:

where, $c_{al}$ represents the $A$-phase sudden change current logic value of the $l$-th equipment of the feeder; $c_{bl}$ represents the $B$-phase sudden change current logic value of the $l$-th equipment of the feeder; $c_{cl}$ represents the $C$-phase sudden change current logic value of the $l$-th equipment of the feeder; $a_{al}$, $b_{al}$ and $c_{al}$ represent the $A$, $B$ and $C$ phase current change values of the $l$-th device in the feeder mutation current array $ACM$ respectively; $\beta$ represents the threshold coefficient, the value range is (0, 1), $WV$ represents the capacitor current threshold, and its value is the same as line type, line length and number of substation outgoing loops are all relevant.

If the feeder mutation logic array $ASM$ is a zero array, it means that the feeder has no ground fault; if $ASM$ is a non-zero array, it means that the feeder has a ground fault, and the row where the non-zero element is located indicates the phase difference of the ground fault.

If the elements in the $\tau \left(\tau =\mathrm{1,2},3\right)$-th row of the feeder mutation logic array $ASM$ are non-zero, all non-zero elements are extracted to form the mutation current logic table $ACG$, which is specifically described as:

where, $c{g}_u$ represents the device number represented by the $u$-th logical 1 element in the $\tau$-th row of $ACG$, $u=\mathrm{1,2},3...$; $o$ represents the total number of non-zero elements in the $\tau$-th row of $ASM$.

Obviously, $ACG$ is an unordered table, and $ACG$ is reordered from parent to child according to the parent-child relationship of the equipment, and the mutation current logical order table $ACXG$ is obtained. The specific description is as follows:

where, $c{x}_w$ represents the device number, $w=1,\mathrm{}2,\mathrm{}3...$; $c{x}_{w-1}$ represents the device number of the parent node of the device $c{x}_w$; $c{x}_{w+1}$ represents the device number of the child node of the device $c{x}_w$.

From the above analysis, it can be seen that the ground fault occurs in the minimum fault judgment interval where the last element $c{s}_u$ of the abrupt current logical sequence table $ACXG$ is the parent node, thus realizing the low-current ground fault judgment of the primary and secondary integrated equipment [14, 15].

5. Experimental studies

In order to verify the validity of the proposed method for judging the low-current grounding fault of the primary and secondary fusion complete sets of equipment under the calculation of three-phase asymmetric harmonic power flow, experiments were carried out.

5.1. Experimental situation

Experiments were carried out on the RTplus real-time digital simulation system to examine the ground fault discrimination function of the primary and secondary fusion equipment. The pilot is located in a 35 kV substation, which has 7 outgoing lines, all of which are located in mountainous areas and are prone to failures. Since August 2015, 25 ground faults have occurred since the installation of primary and secondary fusion equipment with grounding function on the 7 outgoing lines. It is used as an experimental pilot to verify the discriminative effect of the proposed method. The simulated experimental system is shown in Fig. 3. A complete set of primary and secondary fusion equipment is installed on each outlet line, the main transformer is grounded through the arc suppression coil, and the total capacitance current of the system is 15 A.

Fig. 3System diagram of small current ground fault discrimination experiment

5.2. Analysis of experimental results

(1) The ground fault is on line 1.

Fig. 4 shows the three-phase voltage and current and zero-sequence voltage and current waveforms on line 1 measured by switch 1. After the fault, the zero sequence current on line 1 is 6.3 A. The bottom part of Fig. 4 is the use of db4 wavelet and db5 wavelet to extract the peak waveform of the high-frequency part of the zero-sequence current.

It can be seen from Fig. 4 that at the moment of the fault, the zero sequence current has a high-frequency component. The high-frequency value of db wavelet is extracted and compared with the average value of high-frequency values in other segments of wavelet in the power frequency cycle to obtain a multiple. The multiple value obtained by db4-8 wavelet is shown in Table 1.

Table 1Multiples table of db4-8 wavelet analysis results when line 1 fails

db wavelet	4	5	6	7	8
Multiple	87	73	91	112	100

As shown in Table 1, if the fault threshold is set to 30 and multiple thresholds are greater than 30, it can be determined that line 1 where the switch is located is a ground fault line.

(2) The ground fault is on line 2.

Fig. 5 shows the three-phase voltage and current and zero-sequence voltage and current waveforms on line 1 measured by switch 1. After the fault, the zero sequence current on line 1 is 3.2 A.

Fig. 4Waveform diagram of wavelet high-frequency analysis results of line 1 primary and secondary fusion equipment

Fig. 5Waveform diagram of wavelet high-frequency analysis results of line 2 primary and secondary fusion equipment

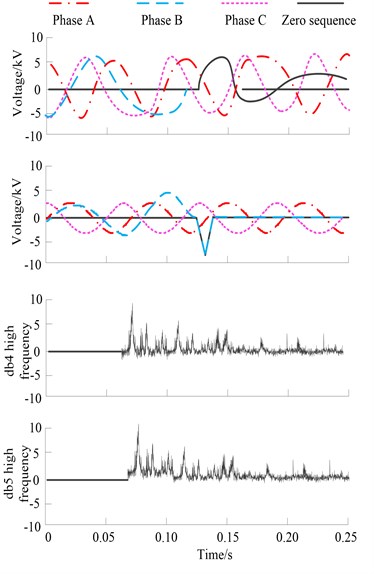
In the lower part of Fig. 5, db4 wavelet and db5 wavelet are also used to extract the peak waveform of the high-frequency part of zero sequence current. See Table 2 for the multiple value obtained by db4-8 wavelet.

Table 2Multiples table of db4-8 wavelet analysis results when line 2 is faulty

db wavelet	4	5	6	7	8
Multiple	7.0	7.4	8.1	8.2	7.5

As can be seen from Table 2, the threshold for judging faults is set to 30, and all times are not greater than this value. You can determine the line where the switch is located, that is, line 1 is not a grounding fault line. The above experimental simulation results verify the accuracy of the proposed method.

(3) Verification of the accuracy of ground fault discrimination.

In order to further verify the effectiveness of the proposed method, five factors that may affect the ground fault discrimination were mainly considered during the test, as shown in Table 3.

Under different influencing factors, the ground fault occurs on the simulated feeder, and the ground fault discrimination and processing functions of the primary and secondary fusion equipment of the proposed method are evaluated. The experimental results are shown in Table 4.

From the experimental results shown in Table 4, the ground fault discrimination results of the primary and secondary fusion equipment meet the expected requirements, which proves that the proposed method is feasible and can meet the discrimination requirements. The method has high judgment accuracy in practical application, and the highest value of judgment accuracy reaches 98.5 %, and there is no false alarm of ground fault on non-faulty lines, indicating that the method has high stability.

Table 3Factors affecting ground fault discrimination

Serial number	Influencing factors	Remark
1	Grounding method	Ungrounded, grounded by arc suppression coil
2	Fault transition resistance	1-1000 Ω
3	Fault type	Stability grounding, arc grounding
4	Fault location	Beginning, end, middle of the line
5	Faulty phase	A, B, C

Table 4Ground fault test results

Fault type	Fault transition resistance / Ω	Ground fault recognition rate / %
Stable ground	0-500	98.5
	1000	97.9
Arc ground	0-500	98.0
	1000	97.8

6. Conclusions

In order to realize the accurate judgment ground fault, improve the effect of fault identification, considering the single phase has been difficult to meet the needs of today’s harmonic power flow calculation, and no convergence problem may emerge in the traditional algorithm, based on the asymmetric three-phase harmonic power flow calculation, for a quadratic convergence complete equipment for small current grounding fault. The final experimental results show that the method can accurately judge the fault line, the highest judgment accuracy is 98.5 %, and can effectively judge whether the ground fault occurs.