Investigation of impact motions in elements of manipulators and robots

Ragulskis, K.; Spruogis, B.; Matuliauskas, A.; Mištinas, V.; Ragulskis, L.

doi:10.21595/mme.2021.22240

Mathematical Models in Engineering

Browse Journal

Submit article

Published: 30 September 2021

Check for updates

Investigation of impact motions in elements of manipulators and robots

K. Ragulskis¹

B. Spruogis²

A. Matuliauskas³

V. Mištinas⁴

L. Ragulskis⁵

¹Kaunas University of Technology, K. Donelaičio str. 73, LT-44249, Kaunas, Lithuania

^{2, 3, 4}Department of Mobile Machinery and Railway Transport, Faculty of Transport Engineering, Vilnius Gediminas Technical University, Plytinės str. 27, LT-10105, Vilnius, Lithuania

⁵Department of Systems Analysis, Faculty of Informatics, Vytautas Magnus University, Vileikos str. 8, LT-44404, Kaunas, Lithuania

Corresponding Author:

K. Ragulskis

Cite the article Download PDF

Downloads 685

CrossRef Citations 1

Abstract

Impact interactions take place in the process of dynamic behavior in the elements of manipulators and robots. Their precise investigation is an important engineering problem. A model having one degree of freedom with forced excitation and impacts is investigated. A special procedure for more precise calculation of impacts is proposed. Numerical results for various parameters of the investigated system are presented. The advantage of the application of the proposed procedure for more precise calculations of dynamics of this system is indicated.

1. Introduction

Impact interactions take place in the process of dynamic behavior in the elements of manipulators and robots. Their precise investigation is an important engineering problem.

A model having one degree of freedom with forced excitation and impacts is investigated. A special procedure for more precise calculation of impacts is proposed. Numerical results for various parameters of the investigated system are presented. The advantage of the application of the proposed procedure for more precise calculations of dynamics of this system is indicated.

Basic investigations of vibrations of vibro impact systems are presented in [1]. Vibrations of transmissions and nonlinear effects in them are investigated in [2]. Dynamics of vibromotors and their applications are described in [3]. This paper is based on the results of those three fundamental references.

Nonlinear systems as well as resonances in them are investigated in [4]. Systems with various types of excitations and impacts are analysed in [5]. Nonlinear dynamical systems and their stabilisation are described in [6]. Impacts and dynamics of vibrating systems are analysed in [7]. Mechanical systems and their periodic orbits are investigated in [8]. Nonlinear qualities of vibro-impact energy sink are described in [9]. Interaction of particle and a wall is analysed in [10]. Multibody dynamical system and its frequencies are investigated in [11]. Dynamics of a pendulum in a mechanism is analysed in [12]. Dynamical system with piecewise linearity is investigated in [13]. Vibrating system and its resonant zones are analysed in [14]. Dynamical system with Sommerfeld effect is investigated in [15]. Dynamical system with isolated resonances is analysed in [16].

In this paper the model of the investigated system is described and then the proposed procedure for more precise calculations of impacts is presented. Results for various parameters of the investigated system without application of the proposed procedure and with it are presented.

2. Model of the vibro impact system with forced excitation

The investigated vibro impact system is described by the following equation:

1

\ddot{x} + 2 h \dot{x} + p^{2} x = - f s i n ω t,

where $x$ denotes the displacement of the investigated system, $h$ is the coefficient of viscous damping of the investigated system, $p$ is the eigenfrequency of the undamped system, $f$ is the amplitude of the exciting force, $ω$ is the frequency of the exciting force, $t$ is the time variable and the upper dot denotes differentiation with respect to the time.

When the following conditions are satisfied:

2

x \geq 0,

and

3

\dot{x} > 0,

then it is assumed that:

4

x = 0,

and

5

{\dot{x}}^{+} = - R {\dot{x}}^{-},

where $R$ is the coefficient of restitution and the superscript minus indicates the value before the impact, while the superscript plus indicates the value after the impact.

3. Procedure for improved calculation of impacts in the investigated system

Further $T$ denotes the time step, the subscript $0$ indicates the value at the beginning of a time step and the subscript $T$ indicates the value at the end of a time step.

When the following condition is satisfied:

6

x_{T} > 0,

then the reduced time step is defined as:

7

T_{r} = T \frac{0 - x_{0}}{x_{T} - x_{0}} .

Then it is assumed that:

8

x_{T_{r}} = 0,

9

{\dot{x}}_{T_{r}} = {\dot{x}}_{0} + ({\dot{x}}_{T} - {\dot{x}}_{0}) \frac{T_{r}}{T},

10

{\ddot{x}}_{T_{r}} = {\ddot{x}}_{0} + ({\ddot{x}}_{T} - {\ddot{x}}_{0}) \frac{T_{r}}{T} .

4. Results of investigations of dynamics of the vibro impact system with forced excitation

The following values of the parameters of the vibro impact system with forced excitation were assumed in the presented investigation:

11

ω = 1, f = 1, p = 1 .

Zero initial conditions were assumed, that is:

12

x (0) = 0, \dot{x} (0) = 0 .

The following time step was used:

13

T = \frac{\frac{2 π}{ω}}{100} .

Investigations were performed for three sets of parameters of coefficient of viscous damping and coefficient of restitution: 1) conservative impacts, 2) conservative inter impact motions, 3) fully dissipative behaviour.

4.1. Results of investigation of dynamics of the vibro impact system with forced excitation for the case of conservative impacts

The following values of the parameters of the vibro impact system with forced excitation were assumed in the presented investigation:

14

h = 0.5, R = 1 .

Graphical results of investigation of dynamics of the vibro impact system with forced excitation without application of the procedure for improved calculation of impacts are presented in Fig. 1.

Fig. 1Dynamics of the vibro impact system with forced excitation without application of the procedure for improved calculation of impacts

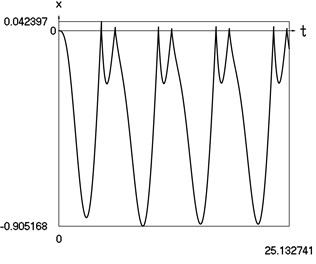
a) Displacement as function of time

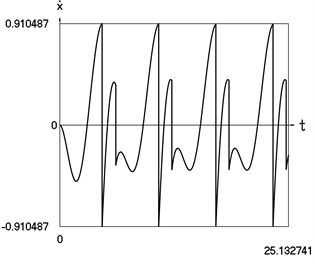
b) Velocity as function of time

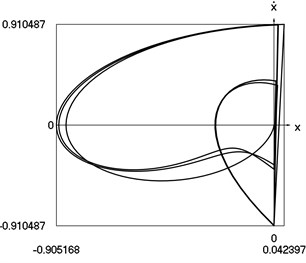
c) Representation in the phase plane: velocity as function of displacement

In Fig. 1 displacement as function of time, velocity as function of time and representation of dynamics of the investigated system in the phase plane are presented.

Graphical results of investigation of dynamics of the vibro impact system with forced excitation with application of the procedure for improved calculation of impacts are presented in Fig. 2.

Fig. 2Dynamics of the vibro impact system with forced excitation with application of the procedure for improved calculation of impacts

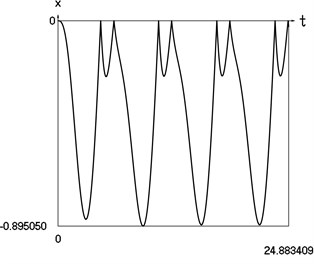
a) Displacement as function of time

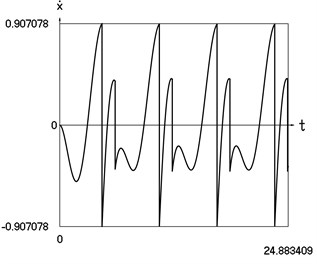
b) Velocity as function of time

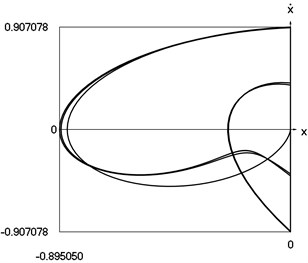
c) Representation in the phase plane: velocity as function of displacement

In Fig. 2 displacement as function of time, velocity as function of time and representation of dynamics of the investigated system in the phase plane are presented.

From the comparison of graphical results presented in Fig. 1 and Fig. 2 it is seen that the procedure of improved calculation of impacts has advantages especially evident in the suppression of small positive values of displacements seen in the process of mutual comparison of drawings a) and c) from those figures.

4.2. Results of investigation of dynamics of the vibro impact system with forced excitation for the case of conservative inter impact motions

The following values of the parameters of the vibro impact system with forced excitation were assumed in the presented investigation:

15

h = 0, R = 0.5 .

Graphical results of investigation of dynamics of the vibro impact system with forced excitation without application of the procedure for improved calculation of impacts are presented in Fig. 3.

In Fig. 3 displacement as function of time, velocity as function of time and representation of dynamics of the investigated system in the phase plane are presented.

Fig. 3Dynamics of the vibro impact system with forced excitation without application of the procedure for improved calculation of impacts

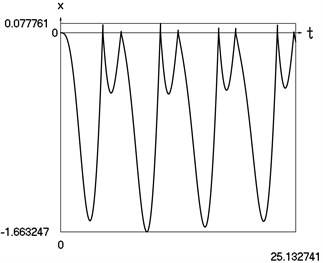
a) Displacement as function of time

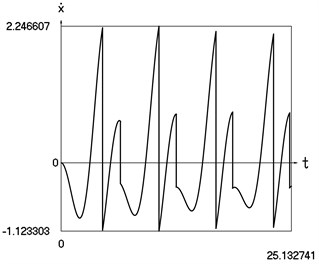
b) Velocity as function of time

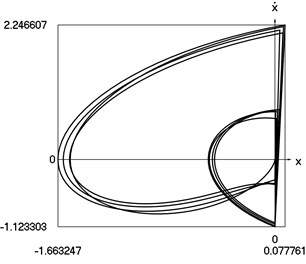
c) Representation in the phase plane: velocity as function of displacement

Fig. 4Dynamics of the vibro impact system with forced excitation with application of the procedure for improved calculation of impacts

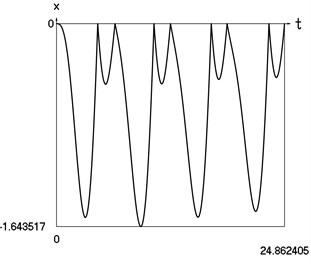
a) Displacement as function of time

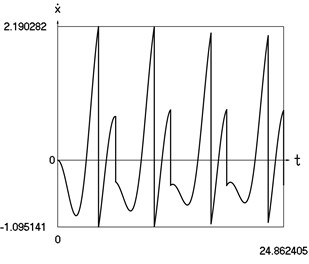
b) Velocity as function of time

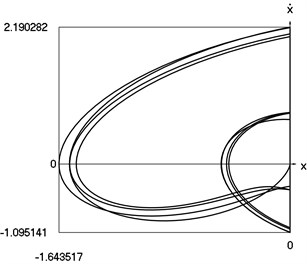
c) Representation in the phase plane: velocity as function of displacement

Graphical results of investigation of dynamics of the vibro impact system with forced excitation with application of the procedure for improved calculation of impacts are presented in Fig. 4.

In Fig. 4 displacement as function of time, velocity as function of time and representation of dynamics of the investigated system in the phase plane are presented.

From the comparison of graphical results presented in Fig. 3 and Fig. 4 it is seen that the procedure of improved calculation of impacts has advantages especially evident in the suppression of small positive values of displacements seen in the process of mutual comparison of drawings a) and c) from those figures.

4.3. Results of investigation of dynamics of the vibro impact system with forced excitation for the case of fully dissipative behaviour

The following values of the parameters of the vibro impact system with forced excitation were assumed in the presented investigation:

16

h = 0.5, R = 0.5 .

Graphical results of investigation of dynamics of the vibro impact system with forced excitation without application of the procedure for improved calculation of impacts are presented in Fig. 5.

Fig. 5Dynamics of the vibro impact system with forced excitation without application of the procedure for improved calculation of impacts

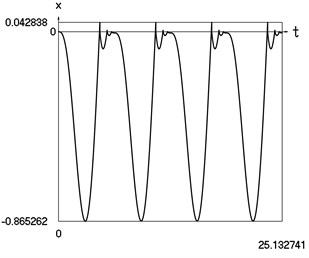
a) Displacement as function of time

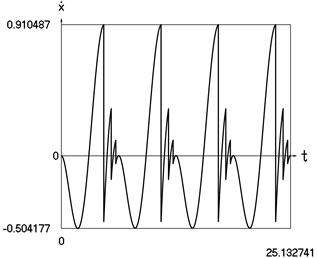
b) Velocity as function of time

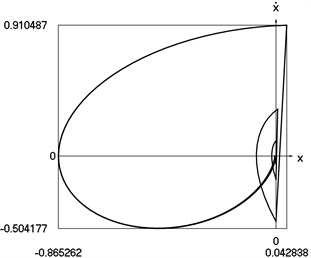
c) Representation in the phase plane: velocity as function of displacement

In Fig. 5 displacement as function of time, velocity as function of time and representation of dynamics of the investigated system in the phase plane are presented.

Graphical results of investigation of dynamics of the vibro impact system with forced excitation with application of the procedure for improved calculation of impacts are presented in Fig. 6.

Fig. 6Dynamics of the vibro impact system with forced excitation with application of the procedure for improved calculation of impacts

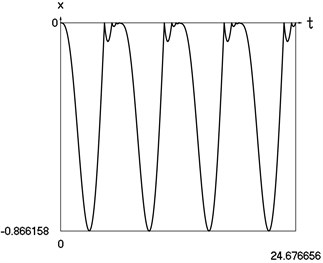
a) Displacement as function of time

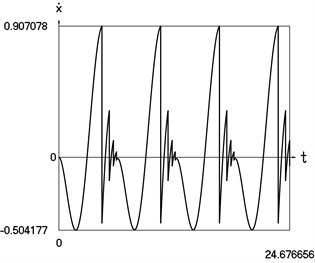
b) Velocity as function of time

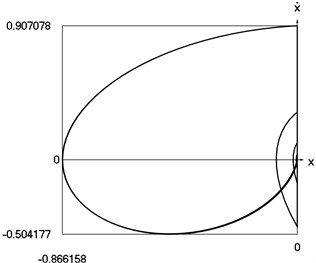
c) Representation in the phase plane: velocity as function of displacement

In Fig. 6 displacement as function of time, velocity as function of time and representation of dynamics of the investigated system in the phase plane are presented.

From the comparison of graphical results presented in Fig. 5 and Fig. 6 it is seen that the procedure of improved calculation of impacts has advantages especially evident in the suppression of small positive values of displacements seen in the process of mutual comparison of drawings a) and c) from those figures.

From the presented graphical results advantages of the proposed procedure for calculation of impact motions are seen.

5. Conclusions

The model of the investigated system is described and then the proposed procedure for more precise calculations of impacts is presented. Results for various parameters of the investigated system without application of the proposed procedure and with it are presented.

Investigations were performed for three sets of parameters of coefficient of viscous damping and coefficient of restitution: conservative impacts, conservative inter impact motions, fully dissipative behaviour. Displacement as function of time, velocity as function of time and representation of dynamics of the investigated system in the phase plane are investigated.

The advantage of the application of the proposed procedure for more precise calculations of dynamics of this vibro impact system with forced excitation is indicated and it is seen from comparisons of some of the graphical results presented which were obtained without application of the proposed procedure and with it. From the comparison of graphical results it is seen that the procedure of improved calculation of impacts has advantages especially evident in the suppression of small positive values of displacements seen in the process of mutual comparison of drawings obtained without application of the proposed procedure and with application of this procedure. From the presented graphical results advantages of the proposed procedure for calculation of impact motions are seen.

The obtained results are used in the process of design of elements of manipulators and robots in which impact interactions take place.

References

Ragulskienė V., Vibro-Shock Systems (Theory and Applications). (in Russian), Vilnius: Mintis, 1974.

Search CrossRef
Kurila R. and Ragulskienė V., Two-Dimensional Vibro-Transmissions. (in Russian), Vilnius: Mokslas, 1986.

Search CrossRef
Ragulskis K., Bansevičius R., Barauskas R., and Kulvietis G., Vibromotors for Precision Microrobots. New York: Hemisphere, 1987.

Search CrossRef
Wedig W. V., “New resonances and velocity jumps in nonlinear road-vehicle dynamics,” Procedia IUTAM, Vol. 19, pp. 209–218, 2016.

Publisher
Li T., Gourc E., Seguy S., and Berlioz A., “Dynamics of two vibro-impact nonlinear energy sinks in parallel under periodic and transient excitations,” International Journal of Non-Linear Mechanics, Vol. 90, pp. 100–110, Jan. 2017, https://doi.org/10.1016/j.ijnonlinmec.2017.01.010

Publisher
V. A. Zaitsev, “Global asymptotic stabilization of periodic nonlinear systems with stable free dynamics,” Systems and Control Letters, Vol. 91, pp. 7–13, May 2016, https://doi.org/10.1016/j.sysconle.2016.01.004

Publisher
H. Dankowicz and E. Fotsch, “On the analysis of chatter in mechanical systems with impacts,” Procedia IUTAM, Vol. 20, pp. 18–25, 2017, https://doi.org/10.1016/j.piutam.2017.03.004

Publisher
Spedicato S. and Notarstefano G., “An optimal control approach to the design of periodic orbits for mechanical systems with impacts,” Nonlinear Analysis: Hybrid Systems, Vol. 23, pp. 111–121, 2017.

Publisher
W. Li, N. E. Wierschem, X. Li, and T. Yang, “On the energy transfer mechanism of the single-sided vibro-impact nonlinear energy sink,” Journal of Sound and Vibration, Vol. 437, pp. 166–179, Dec. 2018, https://doi.org/10.1016/j.jsv.2018.08.057

Publisher
J. S. Marshall, “Modeling and sensitivity analysis of particle impact with a wall with integrated damping mechanisms,” Powder Technology, Vol. 339, pp. 17–24, Nov. 2018, https://doi.org/10.1016/j.powtec.2018.07.097

Publisher
E. Salahshoor, S. Ebrahimi, and Y. Zhang, “Frequency analysis of a typical planar flexible multibody system with joint clearances,” Mechanism and Machine Theory, Vol. 126, pp. 429–456, Aug. 2018, https://doi.org/10.1016/j.mechmachtheory.2018.04.027

Publisher
U. Starossek, “Forced response of low-frequency pendulum mechanism,” Mechanism and Machine Theory, Vol. 99, pp. 207–216, May 2016, https://doi.org/10.1016/j.mechmachtheory.2016.01.004

Publisher
S. Wang, L. Hua, C. Yang, Y. Zhang, Ou, and X. Tan, “Nonlinear vibrations of a piecewise-linear quarter-car truck model by incremental harmonic balance method,” Nonlinear Dynamics, Vol. 92, No. 4, pp. 1719–1732, Feb. 2018, https://doi.org/10.1007/s11071-018-4157-6

Publisher
P. Alevras, S. Theodossiades, and H. Rahnejat, “On the dynamics of a nonlinear energy harvester with multiple resonant zones,” Nonlinear Dynamics, Vol. 92, No. 3, pp. 1271–1286, May 2018, https://doi.org/10.1007/s11071-018-4124-2

Publisher
A. Sinha, S. K. Bharti, A. K. Samantaray, G. Chakraborty, and R. Bhattacharyya, “Sommerfeld effect in an oscillator with a reciprocating mass,” Nonlinear Dynamics, Vol. 93, No. 3, pp. 1719–1739, Aug. 2018, https://doi.org/10.1007/s11071-018-4287-x

Publisher
G. Habib, G. I. Cirillo, and G. Kerschen, “Isolated resonances and nonlinear damping,” Nonlinear Dynamics, Vol. 93, No. 3, pp. 979–994, Aug. 2018, https://doi.org/10.1007/s11071-018-4240-z

Publisher

Cited by

Exciters of vibrations with two pairs of impacting surfaces

K. Ragulskis | P. Paškevičius | L. Ragulskis

(2024)

About this article

Received

07 July 2021

Accepted

27 September 2021

Published

30 September 2021

DOI

https://doi.org/10.21595/mme.2021.22240

Keywords

elements of manipulators

elements of robots

impact interactions

forced excitation

nonlinear behaviour

graphical representations

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous

Research article

2024 03 17

1D manipulator with vibration impact drive, based on which it is possible to create orthogonal manipulators and robots of any dimension

K. Ragulskis, L. Ragulskis

Research article

2023 06 25

Vibrator with two impacting pairs, one of them in the position of equilibrium

K. Ragulskis, L. Ragulskis

Research article

2021 12 02

Mathematical modeling of forced oscillations of semidefinite vibro-impact system sliding along rough horizontal surface

Vitaliy Korendiy, Volodymyr Gursky, Oleksandr Kachur, Volodymyr Gurey, Oleksandr Havrylchenko, Oleh Kotsiumbas

Research article

2021 06 30

Investigation of single valued motions in the vibro-impact system in case of harmonic force

K. Ragulskis, L. Ragulskis

K. Ragulskis, B. Spruogis, A. Matuliauskas, V. Mištinas, and L. Ragulskis, “Investigation of impact motions in elements of manipulators and robots,” Mathematical Models in Engineering, Vol. 7, No. 3, pp. 54–62, Sep. 2021, https://doi.org/10.21595/mme.2021.22240

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/mme.2021.22240
UR  - https://doi.org/10.21595/mme.2021.22240
TI  - Investigation of impact motions in elements of manipulators and robots
T2  - Mathematical Models in Engineering
AU  - Ragulskis, K.
AU  - Spruogis, B.
AU  - Matuliauskas, A.
AU  - Mištinas, V.
AU  - Ragulskis, L.
PY  - 2021
DA  - 2021/09/30
PB  - JVE International Ltd.
SP  - 54-62
IS  - 3
VL  - 7
SN  - 2351-5279
SN  - 2424-4627
ER  - 

Copy Ris

Copied to clipboard!

@article{Ragulskis_2021,
	doi = {10.21595/mme.2021.22240},
	url = {https://doi.org/10.21595/mme.2021.22240},
	year = 2021,
	month = {sep},
	publisher = {{JVE} International Ltd.},
	volume = {7},
	number = {3},
	pages = {54--62},
	author = {K. Ragulskis and B. Spruogis and A. Matuliauskas and V. Mi{\v{s}}tinas and L. Ragulskis},
	title = {Investigation of impact motions in elements of manipulators and robots},
	journal = {Mathematical Models in Engineering}
}

Copy Bibtex

Copied to clipboard!

[1]K. Ragulskis, B. Spruogis, A. Matuliauskas, V. Mištinas, and L. Ragulskis, “Investigation of impact motions in elements of manipulators and robots,” Mathematical Models in Engineering, vol. 7, no. 3, pp. 54–62, Sep. 2021, doi: 10.21595/mme.2021.22240.

Copy IEEE

Copied to clipboard!

Ragulskis, K., B. Spruogis, A. Matuliauskas, V. Mištinas, and L. Ragulskis. “Investigation of Impact Motions in Elements of Manipulators and Robots.” Mathematical Models in Engineering 7, no. 3 (September 30, 2021): 54–62. https://doi.org/10.21595/mme.2021.22240.

Copy Chicago

Copied to clipboard!

Investigation of impact motions in elements of manipulators and robots

Abstract

1. Introduction

2. Model of the vibro impact system with forced excitation

3. Procedure for improved calculation of impacts in the investigated system

4. Results of investigations of dynamics of the vibro impact system with forced excitation

4.1. Results of investigation of dynamics of the vibro impact system with forced excitation for the case of conservative impacts

4.2. Results of investigation of dynamics of the vibro impact system with forced excitation for the case of conservative inter impact motions

4.3. Results of investigation of dynamics of the vibro impact system with forced excitation for the case of fully dissipative behaviour

5. Conclusions

References

Cited by

About this article

Related Articles