Abstract
As an important basis for its structural optimization design, the heat transfer performance has a key influence on the reliability of automobile brake. Based on the finite element method, the transient heat transfer of automobile disc brake is analyzed under the condition of dynamic convection heat transfer coefficient. According to the simulation results, the CCD (Central Composite Design) sampling scheme is used to transform the optimization variable and target variable into multiple design points in the decision space. The optimization variable includes the total thickness, the height of the ventilation slot, the angle between the sides of the ribs, the number of ribs while the target variable includes the mass and temperature peak. According to the multiple quadratic regression model, the response surface function is constructed, and the approximate model of optimization analysis is obtained. The error analysis shows that the response surface function is equipped with good fitting accuracy. In order to facilitate the extremum search, the optimization of the quality is transformed into the constraint condition, and the multi-objective optimization problem of the brake disc is transformed into the single objective optimization problem. Through the sequential quadratic programming method, the Pareto optimal solution set of the optimal mathematical model is found. The results show that the temperature peak value is reduced by 7.8 % under the condition where the quality of the ventilation plate is basically unchanged. By weighting the Pareto optimal solution sets of different quality intervals, a good result evaluation of ventilation panel optimization is achieved.
Highlights
- Based on the DOE optimization scheme, the multi-objective optimization of disc brake is realized.
- According to the sample calculation results, the response surface model is established, which can verify that the accuracy of the approximate model meets the requirements.
- The CCD method is applied to realize discrete data sampling during the construction of response function, which is the basis for the optimized mathematical model.
1. Introduction
If the heat dissipation capacity of the brake disc is insufficient, the heat generated by friction will not be dissipated in time. When the brake disc is in a high temperature state for a long time, the incidence of hot cracks will be increased, which will have a great impact on the stability of friction coefficient and the linear output of braking torque, and even lead to failure brake [1]. There are two types of brake discs, ventilation type and solid type. The ventilation brake disc has a rib structure, which can effectively increase the heat exchange area when air flows and improve the heat exchange efficiency [2, 3]. However, if the structure and number of ribs are not designed properly, the strength and stiffness of the brake disc, especially the heat transfer capacity, will be greatly affected. If the disk mass is too large or the number of fins is too large, not only the processing cost will be increased, but also the heat exchange efficiency may be reduced. Therefore, in terms of engineering, it is significant to optimize design of the brake disc structure, for the quality and temperature peak value of the ventilation disc is one of the most important indicators to measure the cost performance.
It is difficult and hot to improve the performance to price ratio of brake by advanced structural optimization scheme [4]. The traditional optimization design has a large amount of computation and a long research and development cycle, which makes it difficult to deal with the interaction effects and meet the current needs of multi-disciplinary coupling design and research [5]. With the application of numerical technology in engineering, it has become one of the development trends of optimization design to express more accurate approximation function relationship in local area with less calculation, such as DOE optimization method [6]. Since DOE calculation is simple, it brings great convenience to design optimization. Through selecting regression model, it can fit the complex response relationship and has good robustness [7]. The mathematical theory of this method is well grounded, systematic, practical, and widely applicable. It has gradually become a powerful tool for complex engineering system design. The optimization problem needs to be transformed into a mathematical model first. The optimization variables and objectives of the model are obtained by discrete sampling technology, and the objective function is established. Then, the advanced search algorithm is used to realize the optimal solution or solution set of optimization variables in the range of constraints.
2. Analysis of heat transfer characteristics
2.1. Establishment of finite element model
In this paper, ANSYS / workbench is used for the parametric modeling of ventilation disc with finite element analysis [8]. For the disc brake, the moving effect of friction heat source is not obvious under the condition of high speed. Therefore, in order to facilitate the parameter structure optimization of the ventilation disc, the brake pad model is omitted, and the friction surface within one week of the brake pad is separated as the bearing surface through freezing and plane cutting method, and the thermal load and boundary condition are considered to have axial symmetry characteristics. Without affecting the optimization results, such treatment effectively improves the calculation efficiency.
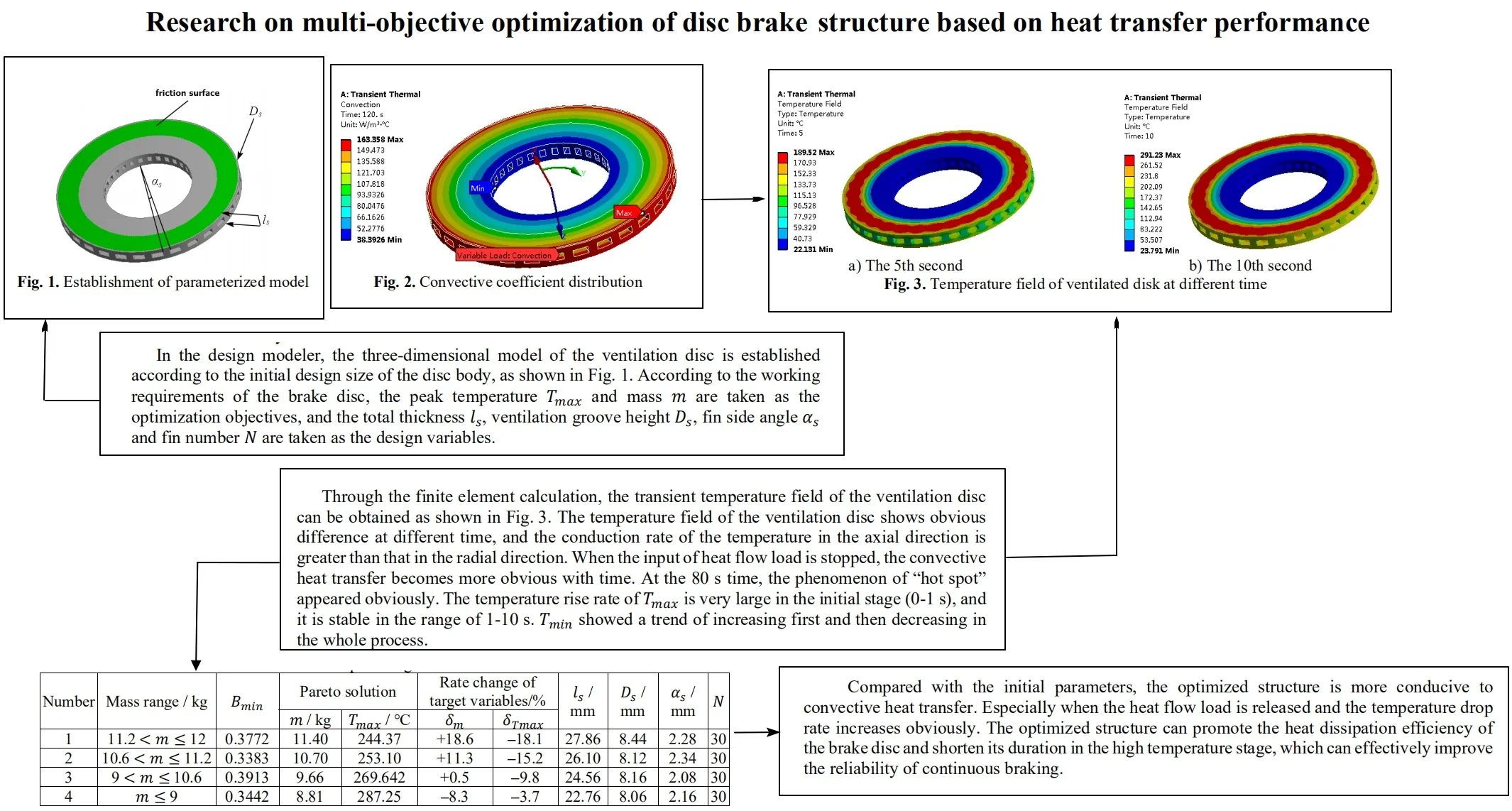
In the design modeler, the three-dimensional model of the ventilation disc is established according to the initial design size of the disc body, as shown in Fig. 1. According to the working requirements of the brake disc, the peak temperature and mass are taken as the optimization objectives, and the total thickness , ventilation groove height , fin side angle and fin number are taken as the design variables.
Fig. 1Establishment of parameterized model
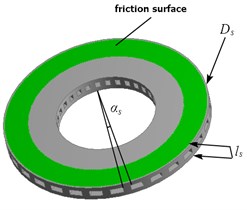
Fig. 2Convective coefficient distribution
Because the key content of the model optimization is the heat transfer performance of the ventilation disc, the stress problem of the model can be ignored, and the transient heat transfer problem of the model can be solved in the transit thermal module. The total time of heat transfer analysis is 120 s and the time step is 1 s. The temperature field distribution of the model is calculated under the condition of constant speed downhill braking for 10 s. The preprocessing of the model mainly includes mesh generation, load application and the definition of boundary conditions. In order to ensure the accuracy of calculation, the tetrahedral structure grid type with a large degree of correlation is used to mesh the model. Finally, the number of mesh elements is 94338, and the number of nodes is 152023 Through the calculation of heat flow density (1 MPa, 60 km/h), the heat flow load of friction surface in 10 s is defined as 8.2×105 w/m2 by tabular data. The thermal radiation direction is defined as 0.28, and ambient temperature is 20 ℃. Establish the cylindrical coordinate system, and define the convection heat transfer coefficient of the end face of the ventilation disc and the ventilation groove surface respectively according to the vehicle speed. The convection heat transfer coefficient is shown in Fig. 2.
2.2. Result analysis
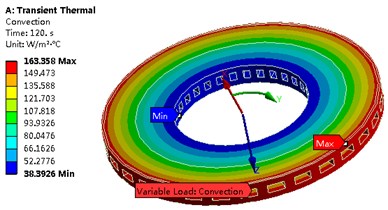
Through the finite element calculation, the transient temperature field of the ventilation disc can be obtained as shown in Fig. 3. The temperature field of the ventilation disc shows obvious difference at different time, and the conduction rate of the temperature in the axial direction is greater than that in the radial direction. When the input of heat flow load is stopped, the convective heat transfer becomes more obvious with time. At the 80 s time, the phenomenon of “hot spot” appeared obviously. The temperature rise rate of is very large in the initial stage (0-1 s), and it is stable in the range of 1-10 s. showed a trend of increasing first and then decreasing in the whole process.
Fig. 3Temperature field of ventilated disk at different time
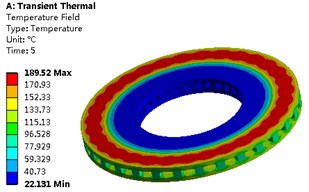
a) The 5th second
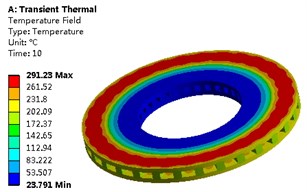
b) The 10th second
3. Construction and solution of optimized mathematical model
3.1. Response function fitting and accuracy checking
The response surface model is also called the fitting function, which can obtain objective function with discrete data, including design variables and target variables (optimization objectives). The CCD (Central Composite Design) method is applied to realize discrete data sampling during the construction of response function, which is the basis for the optimized mathematical model [9]. This method can save the sampling time and shorten the single sampling period on the premise of sufficient sample data. In addition, it can intuitively show the influence of parameter change on performance. Given the cost of manufacturing process, the range of design variables is defined as shown in Table 1. By using the values of the four optimization variables, 145 sample design points combination (including initial values) in the decision space can be constructed.
Given the interaction between structural parameters, the second-order polynomial is used to obtain the response surface function. Define as , as , as and as , the fitting objective function can be expressed as follows:
where , , are undetermined regression coefficient.
According to the least square method, the regression analysis of error can be obtained:
where is the actual discrete response value that obtained from FEA, is the number of samples. Then the regression coefficient of fitting function can be solved by Matlab. According to the fitting principle, it can be known that the error of response surface model is inevitable. In order to ensure the reliability of the optimized mathematical model, it is necessary to verify the fitting accuracy. If the error is within the allowable range, it can prove that the response surface function designed in this paper has good feasibility. The fitting accuracy of response surface function is evaluated by four parameters, including fitting decision coefficient , correcting decision coefficient and root mean square error RMS. The error checking results of response surface functions are calculated. It can be seen that the fitting function is equipped with good fitting accuracy and can effectively ensure the reliability of the optimization results.
Table 1Range of design variable
Design variable | / mm | / mm | /° | |
Initial value | 25 | 10 | 3 | 26 |
Upper limit value / lower limit value | 20/30 | 7/13 | 2/4 | 22/30 |
3.2. Construction of optimized mathematical model
In order to improve the efficiency of optimization calculation, the multi-objective optimization problem is transformed into the single-objective optimization problem [10, 11] when the optimization mathematical model is constructed. In other words, the mass objective function should be transformed into constraints within a specific range. According to the mass and temperature peak value under the initial structure of the brake disc, the searching range of the mass is set as less than 9.6 kg and the temperature peak is set as less than 298 ℃. The objective function and constraint function can be represented respectively as follows:
where is the design variable matrix; is the mass response function; is the temperature peak response function; is the initial value of the optimization target calculated for the parameter test sample; is lower limit of design variables; is upper limit of design variables (search results of need to be integers).
Through continuous iteration operation, the Pareto solution sets [12] of temperature peaks in different mass ranges can be obtained as in Fig. 4, and all the solutions satisfy the optimization mathematical model. In order to verify the optimization results of heat transfer performance, a set of solutions is randomly selected for finite element calculation (20.04 mm, 2.29°, 8.26 mm, 30). Keeping the load and boundary conditions of the finite element model unchanged, the maximum and minimum temperature curves of the brake disc before and after optimization can be shown more clearly by setting the total analysis time of 120 s (braking pressure is canceled during 10th-120th second, no heat source input). It can be seen that the optimized structure is more conducive to heat transfer than the initial parameters, especially when the heat flow load is relieved, the temperature drops significantly, thus promoting the heat dissipation efficiency of the brake disc. It can shorten the time of continuous high temperature stage and effectively enhance the reliability of continuous braking.
The optimization results must meet the cost performance requirements of disc brakes, but the mass and temperature peaks in the optimization objectives are different dimension parameters [13], so it is impossible to evaluate the performance directly from the results. Therefore, a weighted normalization evaluation method is proposed to standardize the data of the optimization objectives [14].
Fig. 4Pareto solution of objective function in different mass ranges
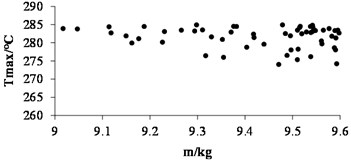
a) 9 9.6
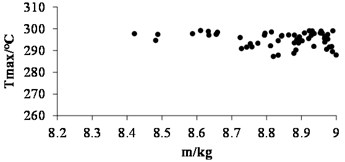
b)9
3.3. Weighted normalization
In weighted normalization, the objective decision value of any Pareto solution of the optimization objective can be expressed as:
According to the manufacturer's agreement, the weighting coefficient of is 0.5. The Pareto solutions in different mass ranges are weighted and normalized by expanding the mass interval, and finally the scatter plots of the target decision-making values in four mass ranges are obtained as shown in Fig. 5. The minimum of objective decision value and the corresponding solution results are shown in Table 3, including the rate change of target variables and structural parameters.
Fig. 5Scatter plot of target decision value under different mass
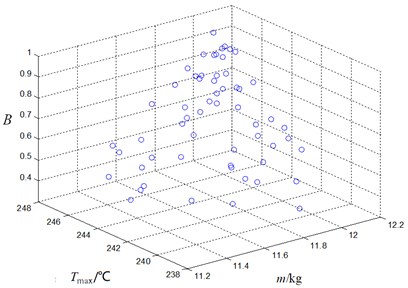
a) 11.2 12 kg
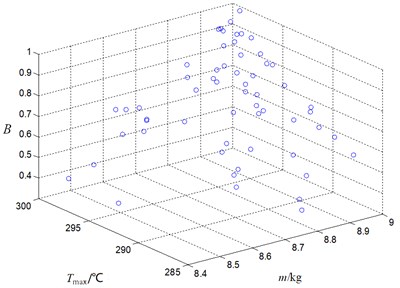
b)9 kg
As can be seen from Table 2, the value in Number 2 is the smallest. Compared with the initial value, the mass increases by 11.3 %, and the peak temperature decreases by 15.2 %. According to the corresponding structural parameters in serial Number 2, the brake disc is manufactured, and the noise level is tested with the same brake pad and load conditions.
Table 2The optimizing decision results
Number | Mass range / kg | Pareto solution | Rate change of target variables/% | / mm | / mm | / mm | ||||
/ kg | / ℃ | |||||||||
1 | 11.2 12 | 0.3772 | 11.40 | 244.37 | +18.6 | –18.1 | 27.86 | 8.44 | 2.28 | 30 |
2 | 10.6 11.2 | 0.3383 | 10.70 | 253.10 | +11.3 | –15.2 | 26.10 | 8.12 | 2.34 | 30 |
3 | 9 10.6 | 0.3913 | 9.66 | 269.642 | +0.5 | –9.8 | 24.56 | 8.16 | 2.08 | 30 |
4 | 9 | 0.3442 | 8.81 | 287.25 | –8.3 | –3.7 | 22.76 | 8.06 | 2.16 | 30 |
4. Conclusions
Based on the DOE optimization scheme, the multi-objective optimization of disc brake is realized. The optimization results effectively improve the heat transfer capacity and cost performance of the disc body, thus improving the thermal fatigue resistance and thermal stability of the brake. In addition, the optimized structure of the ventilation disc can be applied to different types of locomotives, with good economic and social benefits. The conclusions are as follows:
1) For DOE optimization, it is necessary to select a reasonable parameter test sample design scheme, sample within the range of design variables, and calculate the optimization objective according to the spatial decision data. According to the sample calculation results, the response surface model is established, which can verify that the accuracy of the approximate model meets the requirements.
2) Compared with the initial parameters, the optimized structure is more conducive to convective heat transfer. Especially when the heat flow load is released and the temperature drop rate increases obviously. The optimized structure can promote the heat dissipation efficiency of the brake disc and shorten its duration in the high temperature stage, which can effectively improve the reliability of continuous braking.
References
-
L. X. Wang, Y. Y. Gao, and L. Q. Peng, “ANSYS analysis on thermal structure of bionic brake discs,” Journal of Jiangsu University, Vol. 789-790, No. 4, pp. 430–435, 2015.
-
Y. Lei, X. Chen, B. Zhang, and Q. Chen, “Integrated optimization of the fractionation and heat exchange processes in delayed coker with considering steam generation,” Shiyou Xuebao, Shiyou Jiagong/Acta Petrolei Sinica (Petroleum Processing Section), Vol. 31, No. 2, pp. 572–582, Apr. 2015, https://doi.org/10.3969/j.issn.1001-8719.2015.02.040
-
A. L. Nosko, V. V. Mozalev, A. P. Nosko, A. V. Suvorov, and V. N. Lebedeva, “Calculation of temperature of carbon disks of aircraft brakes with account of heat exchange with the environment,” Journal of Friction and Wear, Vol. 33, No. 4, pp. 233–238, Jul. 2012, https://doi.org/10.3103/s1068366612040071
-
E. B. Kosmatopoulos, “An adaptive optimization scheme with satisfactory transient performance,” Automatica, Vol. 45, No. 3, pp. 716–723, Mar. 2009, https://doi.org/10.1016/j.automatica.2008.09.014
-
A. D. Mcphee and D. A. Johnson, “Experimental heat transfer and flow analysis of a vented brake rotor,” International Journal of Thermal Sciences, Vol. 47, No. 4, pp. 458–467, Apr. 2008, https://doi.org/10.1016/j.ijthermalsci.2007.03.006
-
R. B. Patel, N. M. Patel, M. R. Patel, and A. B. Solanki, “Optimization of robust HPLC method for quantitation of ambroxol hydrochloride and roxithromycin using a DoE approach,” Journal of Chromatographic Science, Vol. 55, No. 3, pp. 275–283, Mar. 2017, https://doi.org/10.1093/chromsci/bmw182
-
T. Qiu, A. Zhao, F. Xia, W. Si, and D. O. Wu, “ROSE: robustness strategy for scale-free wireless sensor networks,” IEEE/ACM Transactions on Networking, Vol. 25, No. 5, pp. 2944–2959, Oct. 2017, https://doi.org/10.1109/tnet.2017.2713530
-
S. Chakraborty and A. Sen, “Adaptive response surface based efficient finite element model updating,” Finite Elements in Analysis and Design, Vol. 80, No. 4, pp. 33–40, Mar. 2014, https://doi.org/10.1016/j.finel.2013.11.002
-
S.-E. Fang, Q.-H. Zhang, and W.-X. Ren, “An interval model updating strategy using interval response surface models,” Mechanical Systems and Signal Processing, Vol. 60-61, No. 2, pp. 909–927, Aug. 2015, https://doi.org/10.1016/j.ymssp.2015.01.016
-
K. Deb and H. Gupta, “Introducing robustness in multi-objective optimization,” Evolutionary Computation, Vol. 14, No. 4, pp. 463–494, Dec. 2006, https://doi.org/10.1162/evco.2006.14.4.463
-
C. Mohanty, “Studies on some aspects of multi-objective optimization: a case study of electrical discharge machining process,” Journal of the Electrochemical Society, Vol. 146, No. 10, pp. 3295–3299, 2015.
-
P. J. Attar and E. H. Dowell, “Stochastic analysis of a nonlinear aeroelastic model using the response surface method,” Journal of Aircraft, Vol. 43, No. 4, pp. 1044–1052, Jul. 2006, https://doi.org/10.2514/1.17525
-
X. Wang, “SQP algorithms in balancing rotating machinery,” Mechanical Systems and Signal Processing, Vol. 21, No. 3, pp. 1469–1478, Apr. 2007, https://doi.org/10.1016/j.ymssp.2006.06.003
-
Y.-M. Wang and K.-S. Chin, “Technical importance ratings in fuzzy QFD by integrating fuzzy normalization and fuzzy weighted average,” Computers and Mathematics with Applications, Vol. 62, No. 11, pp. 4207–4221, Dec. 2011, https://doi.org/10.1016/j.camwa.2011.10.005
About this article
The paper is supported by school level scientific research projects (BZXYLG2101), China.
