Analysis of dynamic instability of the wheel set of a railway vehicle using the method of generalized hill determinants

1. Introduction

As is well known, the issues related to vibrations of mechanical systems represent a very voluminous section of applied mechanics. This section is based on fundamental domestic and foreign research in field of nonlinear oscillation theory. This section of mechanics has effective methods and a wide range of solved problems. At the same time, development of modern transport equipment constantly puts forward new urgent problematic issues. One of these issues is related to the study of oscillation in elastic systems transport equipment. One of the most effective ways to improve design and reduce energy costs of transport equipment is based study of the phenomenon resonance. In an oscillating system, which is in resonance state, elastic and inertial forces are mutually balanced. And the energy of the exciter oscillations is spent only on overcoming dissipative forces, while the system itself performs its own motion.

2. Materials and methods

The most common method for finding boundary of the instability region is based on the Fourier series. Another method is the use of generalized Hill determinants. The equations of parametric oscillations linear systems with finite number degrees of freedom are generally represented as:

where $q\left(t\right)$ is the vector of generalized coordinates, $A\left(t\right)$, $B\left(t\right)$ and $C\left(t\right)$ square matrices whose elements are real functions of time. It is assumed that the matrix $A\left(t\right)$ is the positive definite for all $t$, and no restrictions are imposed on the other matrices. Unless otherwise stated, all matrix coefficients are continuous periodic functions of time with period $T$:

The frequency corresponding to this period $\omega =2\pi /T$ is called the parametric excitation frequency. We write Eq. (1) in the Cauchy normal form by introducing the vector of phase variables $\overrightarrow{x}$:

The method of generalized Hill determinants [1] is based on representation one of the solutions general Eq. (3) in the form:

where $\overrightarrow{\chi }\left(t\right)$ – $T$ periodic continuous functions:

Characteristic indices. Let the matrix function $G\left(t\right)$ in Eq. (3) be decomposed into a Fourier series in time:

with constant coefficients – matrices $G_k$ and $H_k$. Expanding the periodic vector function in solution Eq. (4) into a similar series, we look for this solution in the form:

where $h$ – is the unknown characteristic exponent, ${\overrightarrow{a}}_k$ and ${\overrightarrow{b}}_k$ – is the unknown number vectors. Substitution of series Eq. (6) and Eq. (7) into Eq. (3) after equating the coefficients for the same functions time leads to an infinite system linear homogeneous algebraic equations. These are equations for the components of the vectors – the coefficients of the series Eq. (7). The condition existence of a nontrivial solution system is that its determinant is equal to zero [3]. Thus, the characteristic exponents h are roots of the algebraic equation:

where $K$ and $E$ – matrices of infinite order and the matrix $E$ – is identity matrix, and matrix $K$ has following block structure:

where $\omega =2\mathrm{\Omega }.$

Note that under sufficiently broad assumptions about properties matrices $G_k$ and $H_k$ the infinite determinant turns out to be convergent. Consequently, reduction to determinants of finite order is allowed [3].

Now we take into account the third harmonic in solving the Mathieu equation:

Further, following the above method, we get:

3. Results and discussion

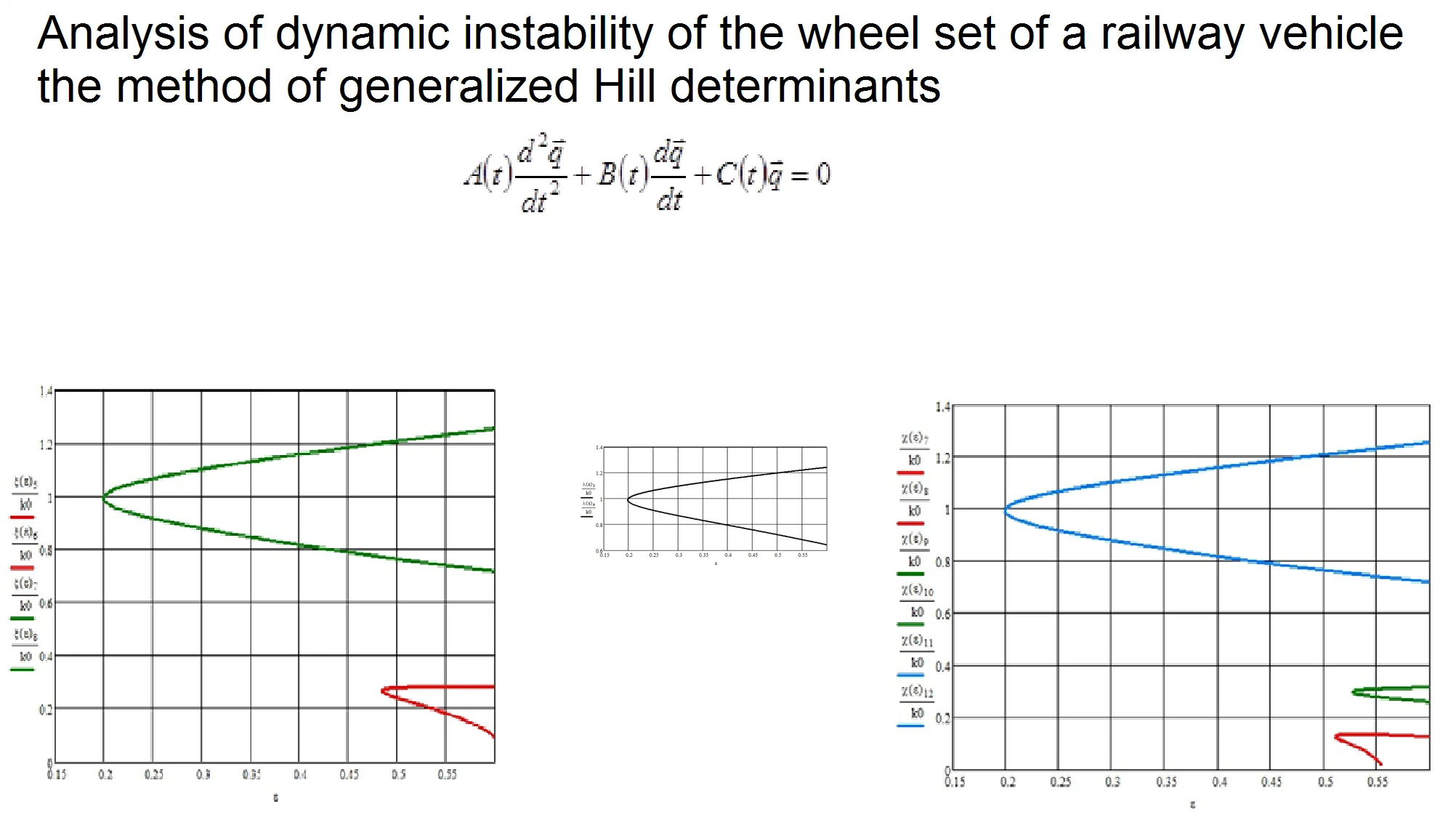
Based on the results of analytical calculations, the authors obtained graphs of the main region of dynamic instability of the wheel set of a railway vehicle. As well parametric resonances when taking into account the third harmonic in solving the Mathieu equation and the zone of instability of the wheel set of the vehicle, taking into account the fifth harmonic in solving the Mathieu equation (see Figs. 1-3).

Fig. 1 shows the main region of dynamic instability of system under consideration.

Fig. 1The main area of dynamic instability wheel set of the vehicle

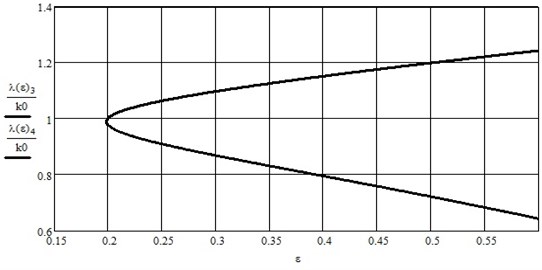
We determine eigenvalues of the matrix Eq. (11) and present results form of the corresponding graphs areas of instability in Fig. 2.

Fig. 2Areas of parametric resonances when taking into account the third harmonics solution of the Mathieu equation

Let us add the fifth harmonic solution of the original equation and after simple transformations, we obtain a matrix of the form:

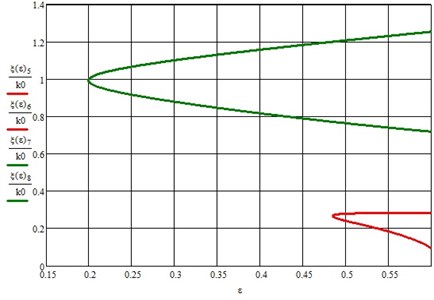
Determining its eigenvalues, we construct the boundaries of the parametric resonance regions shown in Fig. 3.

Fig. 3Zones of instability wheel set of the vehicle taking into account the fifth harmonic solution of the Mathieu equation

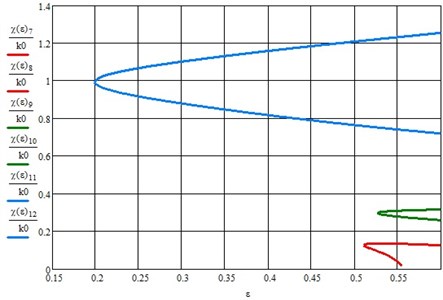
Note here that we have defined only odd zones of dynamic instability. So, to calculate boundaries of the second resonance region, solution of the Mathieu equation must be sought in the form:

It is easy to see that other areas of dynamic instability begin to appear in the figure. Therefore, by continuing to increase number of terms in series Eq. (7), we can refine boundaries of already established parametric resonance zones, while also finding new ones (after all, there are an infinite number of them).

4. Conclusions

As studies have shown, the possibilities of analytical methods are very limited. In practice, they can be used as a rule, only for relatively simple systems and only under certain restrictions on the characteristics of systems. For example, nonlinearity must be weak, i.e. must contain as a factor small parameter and/or random perturbations acting in the system. An analysis of the studies performed showed that in nonlinear problems, each method usually makes it possible to find far from all the statistical characteristics of the system's motion.