Influence of wheelset structural flexibility on dynamic properties of a wide-gauge six-axle heavy-haul locomotive

1. Introduction

Railway vehicle is a coupling system with many degrees of freedom. Some medium- and high-frequency dynamic problems can occur with vehicles and track because of factors such as the high speed and heavy load, but it is difficult to effectively investigate them by using rigid multi-body dynamic methods. One of the effective methods is to use an accurate and reasonable rigid-flexible coupled dynamic model to study the dynamic performance of the vehicle-track coupling system in a wider frequency range [1], [2].

The wheelset is an important part of the rail vehicles. They carry the entire weight of the vehicle system and the forces transmitted from many directions, such as those from the coupling between the wheel and the track. The elastic deformation of the wheelset has an important influence on the characteristics of wheel-rail contacts and the dynamic performance of the vehicle system. In the context of the development of high-speed railways abroad, Popp et al. [3]-[5] carried out earlier systematic studies of the effects of elastic wheelsets on the dynamics of vehicle-track systems. They mainly used the finite element method (FEM) to establish elastic wheelset models. It is concluded that it is necessary to consider the elastic deformations of the wheelsets in the frequency range of 50-500 Hz. Results show that wheelset structural flexibility mainly influences the lateral stability of the vehicle; different wheelset mode shapes have different effects on the dynamic characteristics of the vehicle-track coupling system; and wheelset structural flexibility is one of the important factors to form polygon-shaped wheelsets and to cause rail corrugation.

With the rapid development of the domestic high-speed railway in recent years, the influence of the elastic deformation of the wheelset has been paid more attention to. For example, in [6]-[10], rigid-flexible vehicle-track coupling models were established to investigate the effects of elastic and rigid wheelsets on the dynamic performance of vehicles and the properties of vehicle-track coupling. They carried out combined simulations by using the multi-body dynamic software SIMPACK or UM and the finite element software ANSYS or ABAQUS. The wheelsets were modelled by the FEM while other parts, such as the car body and frame, were regarded as rigid bodies. The results all showed that when the vehicle speed was high or the vehicle ran on the curves, it was necessary to consider the elastic deformation of the wheelset. The response results of the rigid-flexible coupling model could be more reasonable for examining the dynamic performance of the vehicle-track system. Han and Zhang et al. [11] and Zhong et al. [12] investigated the influence of the elastic deformation of the wheelset on the dynamic performance of high-speed railway vehicles as well as the wheel-rail coupling behaviour. Cui et al. [13] and Zhong et al. [14] further studied the rotation effects of the elastic wheelsets on the wheel-rail forces and other dynamic behaviour of high-speed vehicle-track systems.

Heavy-haul transport technology has been recognized as a developmentdirection of railway freight[15], [16]. The increases in the axle weight and freight speed are bound to strengthen the dynamic interaction between the wheel and rail. Thus, many new problems will arise and new challenges will be brought to the dynamic design of heavy-haul railway vehicles [17]-[19]. Gao et al. [20] and Liu et al. [21] studied the elastic deformation of the wheelset and its dynamic effect on a heavy-haul freight wagon with a 30t axle load. Results showed that when the frequency exceeded 20 Hz, the influence of the wheelset structural flexibility on the dynamic performance of the vehicle could be present.

In the above studies, mainly two types of wheelset structures are concerned. One is that the two wheels are rigidly connected to the axle with the axle boxes connected by bearings at both ends of the axle; the other is that there are brake discs installed on the axle. These studies usually ignore the modelling of the axle boxes or equate the masses of the axle boxes to the axle. In fact, for a locomotive vehicle with the motor rigidly suspended on the axle, a large gear will be fixed on the axle deviating from the center, which will directly affect the vibration characteristics of the wheelsets [22], [23]. Meanwhile, the vibration of the axle box has an important influence on the dynamic performance of a vehicle system [24]. It is necessary to model the axle box separately.

For the elastic deformation of the wheelset, most studies focus on the vehicle systems with the B0-B0 type of bogies. Nevertheless, railway vehicles, which have C0-C0 type of bogies, another commonly used type, are seldom examined. In the published literature, Xue et al. [25], Zhang et al. [26] and Spiryagin et al. [27] established rigid multi-body dynamic models of six-axle heavy-haul locomotive-track coupling systems by the commercial software, SIMPACK or GENESYS. And meanwhile, the wheel wear models are established and combined to examine the effects of the wheel wear on the dynamic performance of the locomotives. In the previous paper [28], we established a rigid-flexible vehicle-track coupling dynamic model with elastic wheelsets for a six-axle wide-gauge locomotive by a combined use of the SIMPACK and ANSYS software. The influence of polygonal wheels on the dynamic performance of the locomotive was examined at different speeds. The mass and moment of inertia of the axle box were converted into those of the wheelset in this model, which had a deviation from the actual mass distribution of the wheelset.

In this paper, the vehicle-track coupling model is further improved in Section 2. The axle boxes are modelled separately and it is applied by superposing a vertical short-wave irregularity onto the American fifth-grade track excitation to better study the effect of the elastic deformation of the wheelset. In Section 3, the modal analysis and vibration response characteristics of the rigid and rigid-flexible vehicle systems are compared, respectively. Then in Section 4, according to the relevant national standards of dynamic test and performance evaluation of railway vehicles in wide-gauge railway countries, the influence of wheelset structural flexibility on the vibration response characteristics and dynamic performance of the six-axle heavy-haul locomotive is studied under linear- and curve-track working conditions, respectively, compared to the rigid multi-body dynamic model. Finally, conclusions are drawn in Section 5. The study provides a reference method for the dynamic simulation analysis and performance evaluation of heavy-haul railway locomotives. It is of significance for the equipment design and lightweight research of heavy-haul railway locomotives.

2. Modelling

2.1. Rigid-flexible vehicle-track coupling model with elastic wheelsets

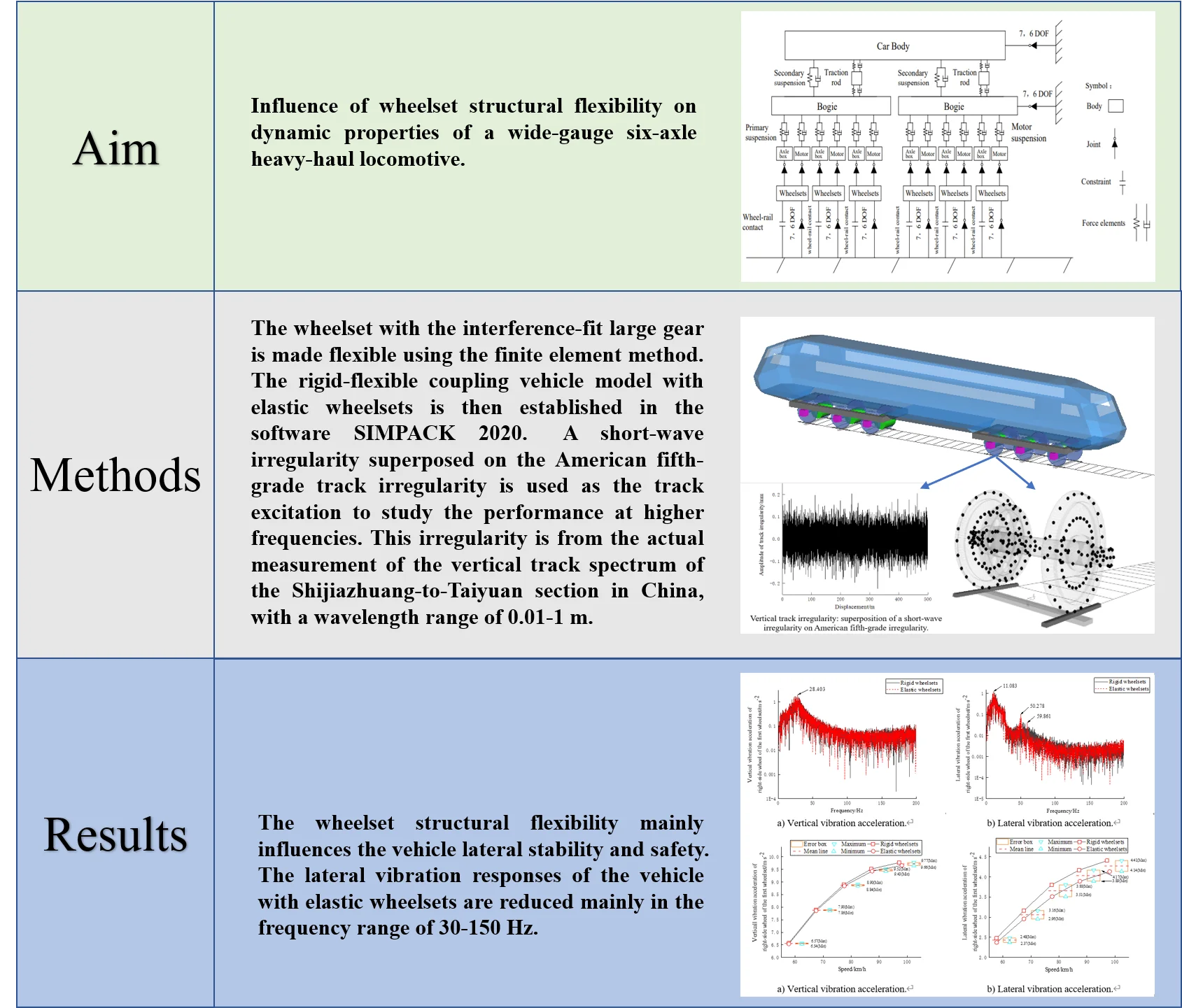
Based on the previous study [28], the present paper improves the rigid-flexible multi-body dynamic model of the six-axle heavy-haul locomotive in the SIMPACK 2020. The main technical parameters and structural characteristics of the bogie of the locomotive are presented in the literature [29]. Fig. 1 shows the topology of the locomotive vehicle and partial parameters used in the model are given in Table 1. Fig. 2 shows the diagram of the rigid-flexible coupling model established in SIMPACK 2020.

Fig. 1Topology of a wide-gauge freight electric locomotive: 7, 6 DOF – 7: general rail track joint, 6 DOF: six degrees of freedom

Table 1Parameters of the wide-gauge locomotive model.

Name	Value	Name	Value
Nominal weight of locomotive	150,000 kg	Longitudinal stiffness of primary suspension	163 MN/m
Car-body weight	95,698 kg	Lateral stiffness of primary suspension	3.3 MN/m
Frame weight	5,756 kg	Vertical stiffness of primary suspension	0.923 MN/m
Wheelset weight	2,672 kg	Longitudinal stiffness of second suspension	0.14 MN/m
Axle-box weight	870 kg	Lateral stiffness of second suspension	0.14 MN/m
Axle weight	25,000 kg	Vertical stiffness of second suspension	5 MN/m

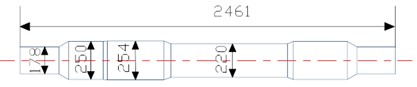
The wide-gauge track model and corresponding wheel tread are used in the vehicle-track coupling model. A Rail-Wheel Pair included in the SIMPACK is set to model the wheel-rail coupling relationship, where the Hertzian contact theory is used for normal force and the Kalker theory for creep force. Fig. 3 gives the structural diagrams of the three components of the wheelset, including the axle, the wheels, and a large gear which are fixed on the axle by interference fit. Wheelset structural flexibility is modelled by the FEM, which will be given in the following section 2.2, where the generation process of the substructure model of the elastic wheelset and some modal information are also detailed. After importing the elastic wheelset into the SIMPACK, the type of body properties is selected as linear flexible because only small elastic deformation of the wheelset is considered. The SIMPACK 2020 has FlexContact to enable users to calculate flexible-rigid contact modelled by using the flexible model.

Fig. 2Rigid-flexible coupling locomotive vehicle model: a) front view; b) top view; c) left view

a)

c)

b)

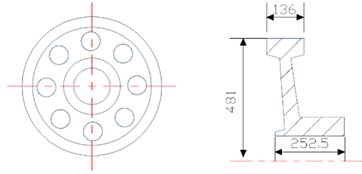
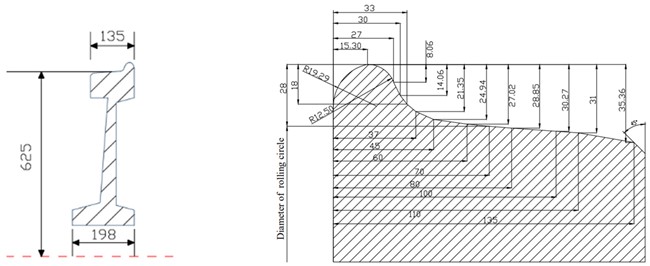
Fig. 3Geometric structures of each part of the wheelset (mm): a) axle; b) front view of large gear (left) and cross-section view of large gear (right); c) cross-section view of wheel (left) and tread size diagram (right)

a)

b)

c)

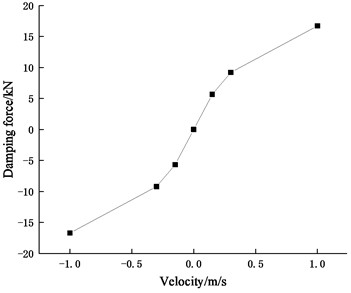
The bogies and car body of the vehicle are modelled as rigid bodies with 6 degrees of freedom based on practical structures. Wheelsets, bogies, and car body are linked by the primary and secondary suspensions. Coil springs and dampers are used in primary suspension and rubber isolators in secondary suspension in this vehicle [29]. The deformations of the springs in primary suspension and the rubber isolators in secondary suspension are considered in three orthogonal translational directions and modelled by linear stiffness and damping models. The dampers in primary suspension are modelled by a piecewise nonlinear model in the vertical direction. The damping force-velocity relationship of the damper is shown in Fig. 4. Separately, the axle boxes and motors are also modelled as rigid bodies with 6 degrees of freedom. The axle boxes are hinged at the ends of the axles and also connected to the corresponding lower points of the primary suspension according to the practical connection relationships. The motors are hinged at the axles, the upper ends of which are connected to the bogies with vertical linear springs.

Fig. 4Damping force-velocity curve of the damper in primary suspension

2.2. Modelling of wheelset structural flexibility

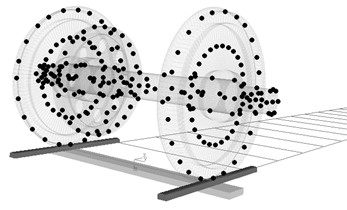
In ANSYS software, after pre-processing, the wheelset is meshed by using the 8-node solid element, Solid185. The mesh size is set as 10 mm. If using 6 elements per wavelength, it’s enough to calculate the dynamic properties at frequencies up to 450 Hz for the maximum velocity of the vehicle as 100 km/h. The hexahedral meshes are in the majority and degenerate into the tetrahedral meshes in some local locations. 356 634 nodes and 329 012 elements are generated. The material parameters are given in Tab 2. Then 261 host nodes with 1 566 degrees of freedom are selected, as shown in Fig. 5. The elastic deformation of the wheelset will be characterized by these host nodes in the rigid-flexible coupling model. Table 3 shows the eigenfrequencies and mode shapes of the wheelset. When modelling wheelset structural flexibility, it is necessary to ensure that the error between the free modes of the wheelset structure by FEM and the substructure reduction modes imported into the SIMPACK software is kept within 5 %.

Table 2Material parameters of the wheelset

Density / (kg/m3)	Modulus of elasticity / GPa	Poisson’s ratios
7 850	210	0.3

Fig. 5Selection of main DOF nodes for the wheelset

a)

b)

Table 3Mode frequencies and shapes of the wheelset [28]

The first torsion	The first bending	The second bending	Big gear swing	Big gear torsion
63.779 Hz	74.691 Hz	111.851 Hz	144.081 Hz	164.155 Hz

2.3. Track spectrum excitation

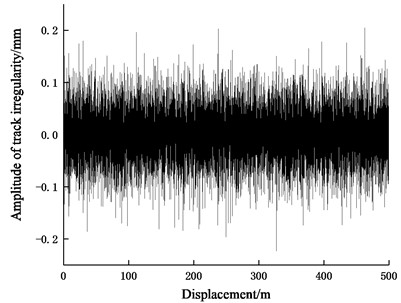
In this paper, the American fifth-grade track irregularity is used as the track spectrum excitation of the vehicle system, the wavelength range of which is in the range of 1.524-304.8 m. In order to better study the medium- and high-frequency vibration characteristics of the elastic wheelsets, a vertical short-wave irregularity is superposed on the American fifth-grade vertical irregularity. The power spectral density function of the short-wave irregularity is approximated as [30]:

1

$S\left(f\right)=0.036f^{-3.15},$

where the unit of $S\left(f\right)$ is mm²/(1/m); $f$ is the spatial frequency with the unit as 1/m. This irregularity is from the actual measurement of the vertical track spectrum of the Shijiazhuang-to-Taiyuan section in China, with a wavelength range of 0.01-1 m. A 500-meter spatial sample of the track irregularity used in this paper is obtained as shown in Fig. 6.

Fig. 6Vertical track irregularity: superposition of a short-wave irregularity on American fifth-grade irregularity

2.4. Vertical wheel-rail force without excitation

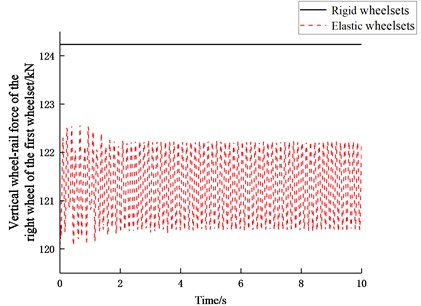
To check the reliability of the rigid-flexible coupling model, the comparison between the rigid model and the rigid-flexible coupling model is carried out by running at 100 km/h on a linear track without excitation. The vertical wheel-rail forces for the two models are shown in Fig. 7. It can be seen that the wheel-rail force of the vehicle model with rigid wheelsets is a constant, which is equal to half of the axle load because there is no outside perturbation for the vehicle. For the vehicle model with elastic wheelsets, the wheel-rail force is harmonic after the vehicle reaches the steady state. This is because a vertical eccentric force acts on the wheel and track as the centres of mass and geometry of the axle are offset resulted from the static deformation of the elastic wheelset. This offset is related to the running speed, track forms (straight and curved), and so on [8], [31], which has an important influence on the wheel-rail contact relationship of high-speed vehicles. The harmonic excitation generated by this offset will act together with the track spectra on the rigid-flexible coupling vehicle model. Nevertheless, since the design speed of the locomotive studied in this paper is 120 km/h and the actual running speed is lower, the effect of the static offset of the axle is negligible in this paper.

Fig. 7Vertical wheel-rail force without excitation

3. Vibration response characteristics of vehicle system

3.2. Vibration response characteristics

The vehicle is set to run at a constant speed of 100 km/h on a 500-metre-long linear track. The track excitation is added between 50 to 500 meters. For comparison, the right-side wheel of the first wheelset, the first motor, and the frame of the first bogie are taken as the research objects. The sampling frequency is set as 500 Hz. Vibration acceleration signals under steady state are analysed in the frequency and time domains. The maximum acceleration values of the time domain results are calculated by the 3$\sigma$ criterion.

3.2.1. Vibration acceleration characteristics of wheel

Figs. 8-9 show the frequency spectra and time domain results of the vibration acceleration of the right-side wheel of the first wheelset, respectively. It can be seen that the elastic deformation of the wheelset has little effect on the vertical vibration characteristics of the locomotive vehicle while has obvious effect on the lateral vibration characteristics. From Fig. 8(b), it can be seen that the lateral vibration acceleration of the wheel of the rigid-flexible coupling vehicle model decreases mainly in the frequency range of 30-150 Hz. Nevertheless, there are two peaks, at frequencies 50.278 Hz and 59.861 Hz respectively, where the first torsion of the wheelset is excited according to the modal analysis.

It can be seen from Fig. 9 that with the increase of the vehicle speed, the vibration acceleration of the wheel of the vehicle model with elastic wheelsets has more reduction compared to the rigid model. It indicates that the wheelset structural flexibility has a certain effect of vibration reduction, especially at higher frequencies, but may induce resonance.

Fig. 8Frequency spectra of vibration acceleration of right-side wheel of the first wheelset at 100 km/h

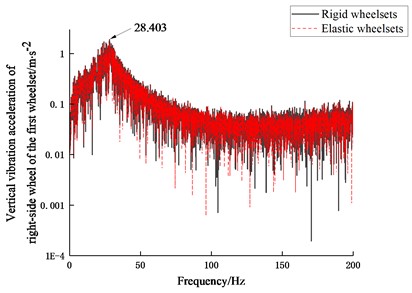
a) Vertical vibration acceleration

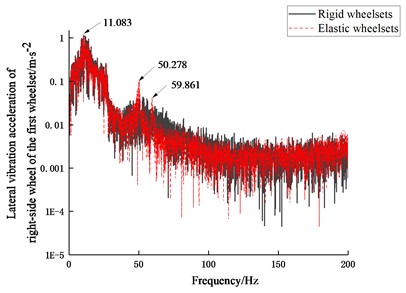
b) Lateral vibration acceleration

3.2.2. Vibration acceleration characteristics of motor

Since the motor is semi-suspended on the bogie and rigidly connected to the axle at the other end, its vibration characteristics are directly influenced by the vibration of the wheelset. As shown in Figs. 10-11, it is obtained that the elastic deformation of the wheelset has little effect on the vertical vibration characteristics of the motor while has obvious effect on the lateral vibration characteristics. The lateral vibration of the motor is reduced compared to the rigid vehicle model.

Fig. 9Maximum values of vibration acceleration of the wheel

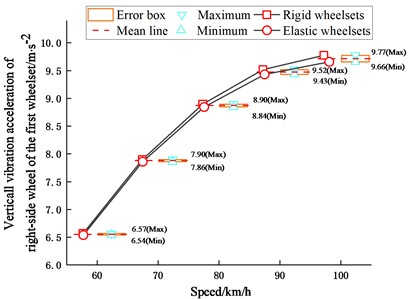
a) Vertical vibration acceleration

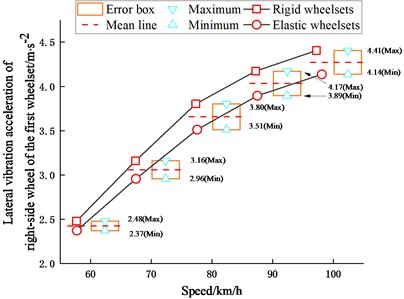
b) Lateral vibration acceleration

Fig. 10Frequency spectra of vibration acceleration of motor at 100 km/h

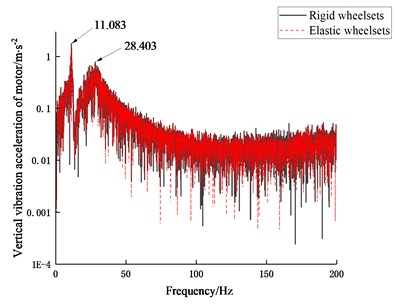
a) Vertical vibration acceleration

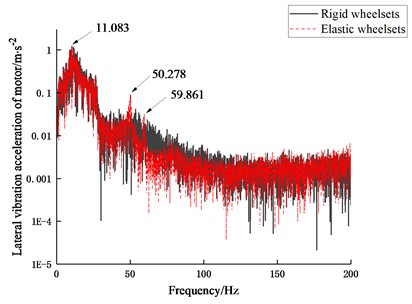
b) Lateral vibration acceleration

Fig. 11Maximum values of vibration acceleration of motor

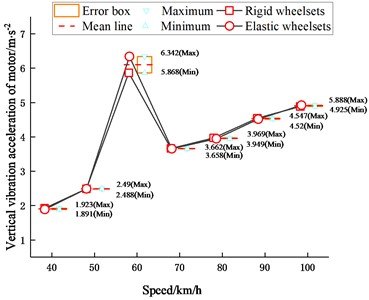
a) Vertical vibration acceleration

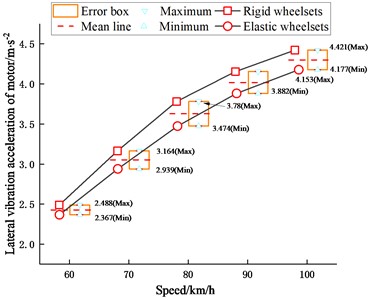
b) Lateral vibration acceleration

The frequency spectrum results in Fig. 10 show that the vertical vibration mode of the motor is excited at the frequency of 11.083 Hz; as shown in Fig. 10(b), the lateral vibration of the motor is mainly reduced in the frequency range of 30-130 Hz. The influence of the wheelset structural flexibility at the two frequencies of 50.278 Hz and 59.861 Hz is also obvious. Moreover, it can be seen from Fig. 11(a) that when the vehicle is running at 60 km/h, the vertical vibration of the motor is significantly increased for both vehicle models. From the comparison of the frequency spectra of the vertical vibration acceleration of the motor at two speeds in Fig. 12 the resonance occurs when the vehicle is running at 60 km/h. In fact, the rotational frequency of the wheel is 4.25 Hz at 60 km/h, whose three-time frequency is close to the modal frequency of the vertical motion of the motor.

Fig. 12Comparison of frequency spectra of vertical vibration acceleration of motor at 60 and 70 km/h

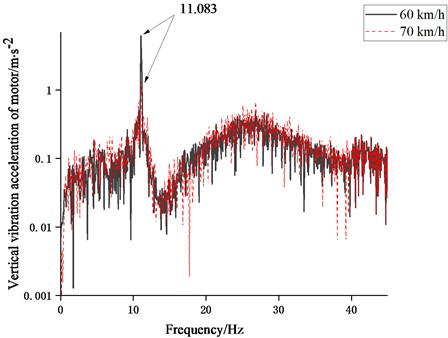
3.2.3. Vibration acceleration characteristics of frame

Similarly, as seen in Figs. 13-14, the wheelset structural flexibility has more effect on the lateral vibration of the frame. From Fig. 13(a) and Fig. 14(a), the wheelset structural flexibility has little effect on the vertical vibration of the frame in the frequency range of 200 Hz when the vehicle is operating at 60-100 km/h. It can be seen from Fig. 13(b) that the vibration of the frame of the rigid-flexible coupling vehicle model is mainly reduced in the frequency range of 30-170 Hz while the resonance occurs at 59.861 Hz. In addition, there are two peaks at 11.944 Hz and 26.458 Hz, corresponding to the nod and vertical motion of the frame, respectively.

Fig. 13Frequency spectra of vibration acceleration of frame at 100 km/h

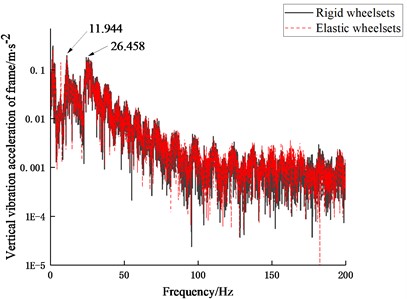
a) Vertical vibration acceleration

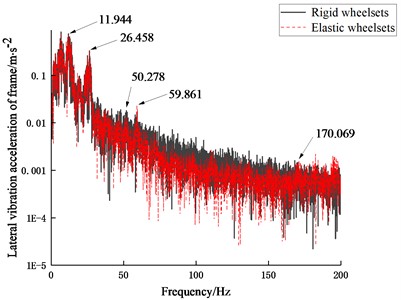
b) Lateral vibration acceleration

4. Effects on dynamic performance of locomotive

ГОСТ P 55495-2013 standard [32] are generally used to evaluate the dynamic performance of wide-gauge locomotive vehicles. The dynamic indicators mainly include the Sperling index (ride comfort), derailment resistance coefficient of the wheel (operation safety), horizontal dynamic load coefficient, and vertical dynamic load coefficients of the suspensions, whose calculation methods have been explained in the previous paper [28]. The vehicle dynamic performance is examined mainly based on these indicators.

Fig. 14Maximum values of vibration acceleration of frame

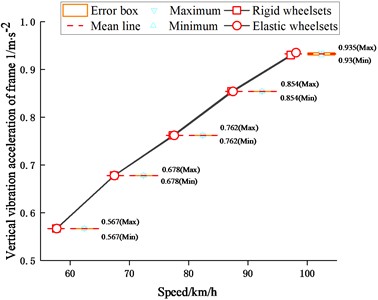
a) Vertical vibration acceleration

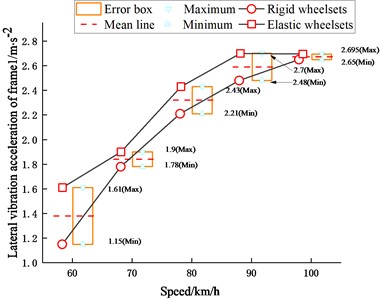
b) Lateral vibration acceleration

4.1. Critical vehicle speed

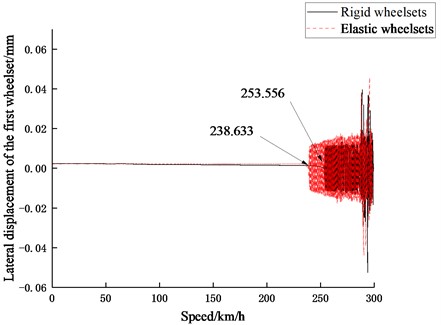
The nonlinear critical speed is calculated based on the deceleration method [33]. The track excitation is added on the first 50 meters. Setting the initial speed as 300 km/h and opening the braking force element for simulation, the vehicle slows down until stops. In the simulation results, the lateral displacement of the wheelset is obtained to evaluate the critical speed of the vehicle. As shown in Fig. 15, the critical speed of the rigid multi-body dynamic vehicle model is 253.556 km/h and that of the rigid-flexible coupling model is 238.633 km/h; it indicates that the wheelset structural flexibility can reduce the critical speed of the vehicle, which is consistent with the results of the related previous studies on the wheelset structural flexibility.

Fig. 15Critical speed of vehicle systems

4.2. On linear track

The vehicle is set to run at speeds of 60 km/h, 70 km/h, 80 km/h, 90 m/h, and 100 km/h, respectively. The Sperling index and wheel-rail force are used to examine the vehicle’s dynamic performance in the linear-track condition.

4.2.1. Sperling index

The vibration acceleration in the seat position of the driver's cab at the front end of the car body is obtained, and the Sperling indexes are calculated to evaluate the ride comfort of the vehicle. As shown in Fig. 16, the wheelset structural flexibility has little effect on the vertical and lateral ride comfort of the vehicle.

Fig. 16Sperling index of the driver's cab

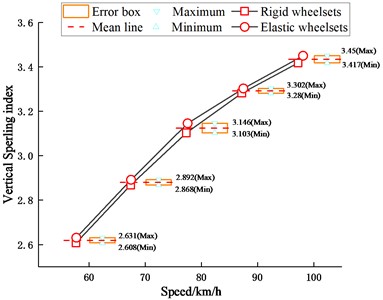
a) Vertical

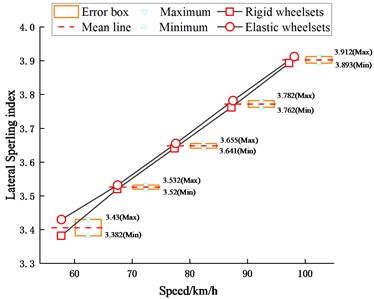
b) Lateral

4.2.2. Wheel-rail force

Wheel-rail dynamic force is one of the important indicators for evaluating vehicle-track dynamics [30]. According to the literature [34], the time domain results of the wheel-rail force are more reliable by using the filtering method of the 97.5th percentile. From the results shown in Fig. 17, it is obtained that the wheelset structural flexibility has a great effect on both vertical and lateral wheel-rail forces. The wheel-rail dynamic forces of the rigid-flexible coupling vehicle model are significantly smaller.

Fig. 17Wheel-rail forces

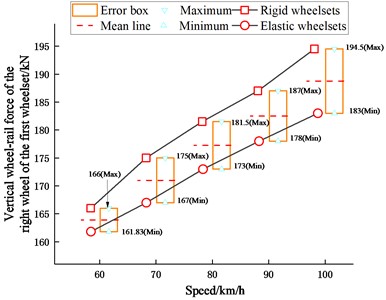
a) Vertical

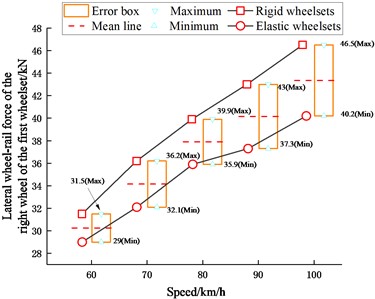
b) Lateral

4.3. On curve track

According to the requirements of the dynamic safety tests of wide-gauge locomotives, a large-radius curve track (curve radius bigger than 600 m) is established [35] with a curve radius of R610 m, the easement curve 60 mm and the superelevation 120 mm. To evaluate the curve-passing performance of the wide-gauge locomotive vehicle, taking the first bogie as the research object, the vertical dynamic load coefficients of the primary and second suspensions and the horizontal dynamic load coefficient are investigated, respectively; taking the right wheel of the first wheelset as the research object, the derailment resistance coefficient of the wheel is investigated; and taking the left wheel of the first wheelset as the research object, the wheel unloading ratio is investigated. For the results, the dynamic load coefficients at different speeds are obtained by using the filtering method of the 3$\sigma$ criterion; other results are obtained by using the filtering method of the 97.5th percentile [34].

4.3.1. Vertical dynamic load coefficient

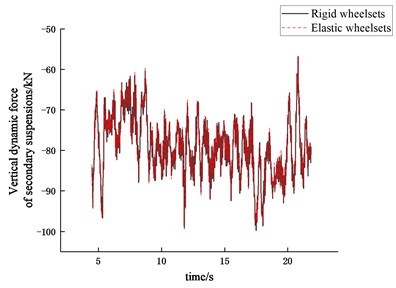
The vertical dynamic load coefficient of the suspension is calculated as the ratio of the vertical dynamic force acting on the upper end of the right suspension device of the first bogie to the vertical static force carried on it. Fig. 18 shows the vertical dynamic load coefficients of the primary and second suspensions when the vehicle is running at different speeds. Figs. 19-20 show the time history of the vertical dynamic force of the primary suspension when the vehicle is running at 40 km/h and that of the second suspension when the vehicle is running at 80 km/h, respectively. It can be obtained that under the curve-track condition, the vertical dynamic load coefficient of the suspension first decreases and then increases rapidly with the increase of the speed because of the influence of the superelevation, but in general, the wheelset structural flexibility has little effect on the vertical dynamic characteristics of the suspension.

Fig. 18Vertical dynamic load coefficients of primary and secondary suspensions

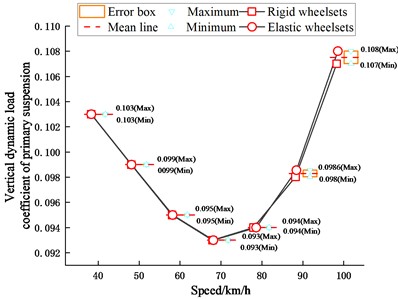
a) Primary suspension

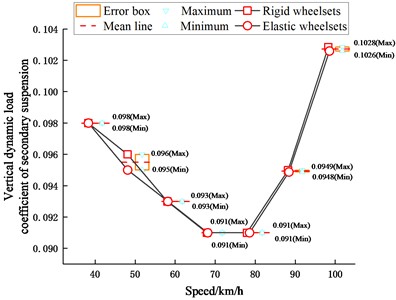
b) Secondary suspension

Fig. 19Time history of vertical dynamic force of primary suspension at 40 km/h

Fig. 20Time history of vertical dynamic force of the second suspension at 80 km/h

4.3.2. Horizontal dynamic load coefficient

The horizontal dynamic load coefficient is calculated using the horizontal dynamic frame force. Fig. 21 shows the horizontal dynamic load coefficients for the vehicle running at different speeds. Figs. 22(a) and (b) show the time histories of the horizontal frame force for the vehicle running at 40 km/h and 80 km/h, respectively. It can be obtained that the horizontal dynamic load coefficient first decreases and then increases rapidly with the increase of the vehicle speed, which is similar to the trend of the vertical dynamic load coefficient. For this vehicle system, the horizontal dynamic load coefficient of the rigid-flexible coupling vehicle model is smaller than that of the rigid vehicle model in the speed range of 40-80 km/h, where the wheelset structural flexibility has an obvious effect; nevertheless, when the vehicle speed is larger than 80 km/h, the influence of the wheelset structural flexibility becomes very small.

Fig. 21Horizontal dynamic load coefficient

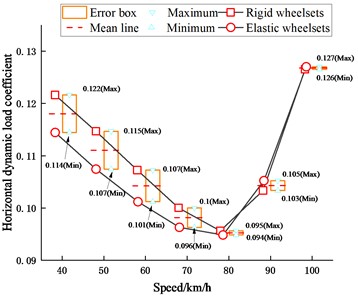
Fig. 22Time history of horizontal frame force

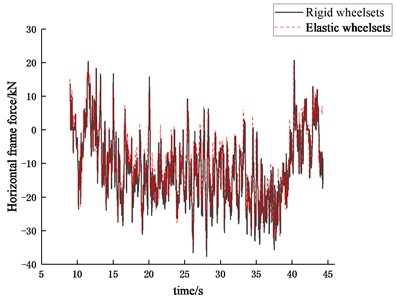
a) 40 km/h

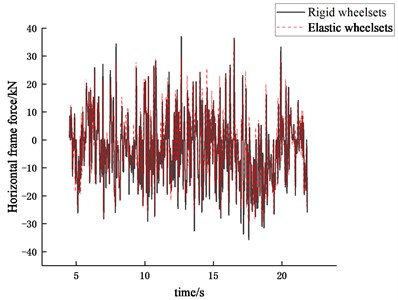
b) 80 km/h

4.3.3. Vehicle safety indicators

Figs. 23-24 show the derailment resistance coefficient of the right wheel of the first wheelset and the wheel unloading ratio of the left wheel of the first wheelset, respectively, when the vehicle is running at different speeds. Figs. 25-26 show the time histories of the derailment coefficient and the wheel unloading ratio when the vehicle running at 40 km/h and 80 km/h, respectively. ГОСТ P 55495-2013 standard uses the derailment resistance coefficient as one of the vehicle safety indicators. The derailment resistance coefficient $\eta$ is calculated as:

2

$\eta \approx 1.48/\lambda ,$

where $\lambda$ is the derailment coefficient. The time histories of the derailment coefficient are given as there is a better expression effect.

From the time domain results, it can be seen that the wheelset structural flexibility has a significant effect on both the derailment resistance coefficient of the wheel and the wheel unloading ratio.

Fig. 23Derailment resistance coefficient of the right wheel

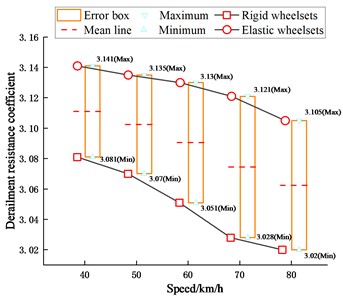
Fig. 24Wheel unloading ratio of the left wheel

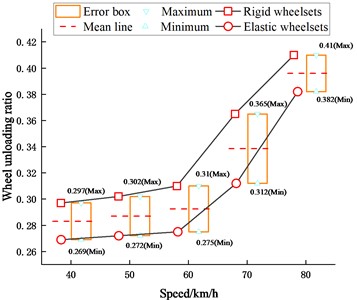
Fig. 25Time history of the derailment coefficient

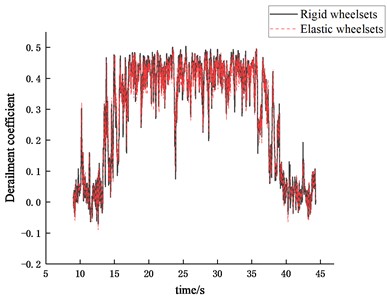
a) 40 km/h

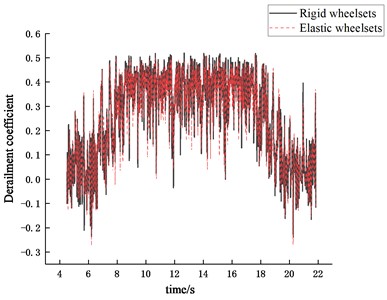
b) 80 km/h

Fig. 26Time history of the wheel unloading ratio

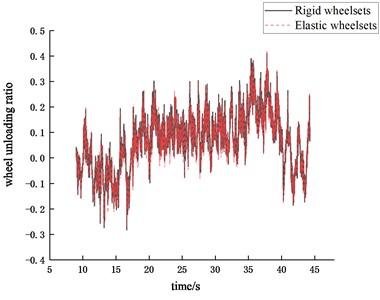
a) 40 km/h

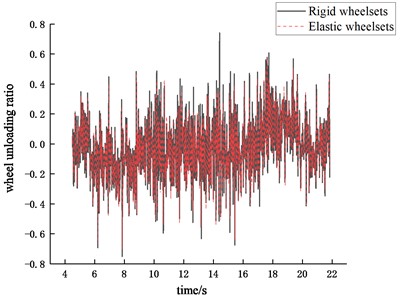
b) 80 km/h

5. Conclusions

This paper takes a wide-gauge freight locomotive with the C0-C0 type of bogies as the research object. The wheelset consists of the axle, two wheels, and a large gear fixed on the axle by interference fit. The wheelset structural flexibility is modelled by the FEM and the rigid-flexible coupling vehicle system model is established. The influence of the wheelset structural flexibility on the vibration response characteristics and dynamic performance of the locomotive vehicle is investigated by comparing it with the rigid multi-body dynamic model and taking the ГОСТ standard as the main evaluation reference.

1) For modelling, to better investigate the influence of the wheelset structural flexibility, the axle box and wheelset are modelled separately as two bodies; the American fifth-grade irregularity with the superposed vertical short-wave irregularity is used as the track excitation. Because of the static deformation of the elastic wheelset, a harmonic excitation will be generated when the vehicle is running at a constant speed and act together with the track excitation.

2) It is obtained from the modal analysis of the locomotive vehicle that the elastic deformation of the wheelset begins to occur from the frequency of 24.631 Hz. According to the results of the acceleration response characteristics of the wheel, motor and frame, the wheelset structural flexibility has a great effect on the lateral vibration properties of the vehicle; the lateral vibration responses of the rigid-flexible coupling vehicle model are reduced mainly in the frequency range of 30-150 Hz. However, resonances occur at the two frequencies of 50.278 Hz and 59.861 Hz, where the rigid-flexible coupling modes occur including the wheelset first torsion. From the results of the free modal analysis of the wheelset, the first torsion, which is the first-order mode shape of the wheelset, occurs at 63.779 Hz. This frequency is close to the above two coupling mode frequencies, so it is easy to give rise to resonance. However, although the first bending mode of the wheelset occurs in the two rigid-flexible coupling modes of the vehicle at the frequencies of 24.631 Hz and 51.614 Hz, no resonance occurs under the excitation condition in this paper. The first bending is the second-order mode shape of the wheelset and the mode frequency is far from the two frequencies, the energy of which is relatively small.

3) From the effect on the dynamic performance of the locomotive, it is obtained that wheelset structural flexibility mainly influences the vehicle lateral stability and safety while almost has no effect on the ride comfort. Compared with the rigid vehicle model, the critical speed of the rigid-flexible coupling model decreases; and in the main speed range of this locomotive running on the curve (40-80 km/h), the horizontal dynamic load coefficient of the rigid-flexible coupling vehicle model is reduced. For the vehicle safety performance, there are also obvious differences in the values of two indicators between the two vehicle models, the derailment resistance coefficient of the wheel and wheel unloading ratio.