Abstract
As one of the important core components of train running parts, the wheel rail related force will directly affect the vehicle running performance and passenger comfort. Take a high-speed train as the research object, the vehicle track coupling dynamic model is established. The influence of wheel polygon on the vibration characteristics of bogie system is analyzed through simulation. The results show that when the wheel polygon wear occurs, the effective value of lateral acceleration of polygonal wheel set axle box is about 18.9 % higher than that of normal wheel set axle box; at the same speed, with the increase of the wave depth of the wheel polygon, the effective values of the transverse and vertical acceleration of the axle box gradually increase; the effective value of axle box vertical vibration acceleration caused by wheel polygon with different amplitude increases first, then decreases and then increases with the change of vehicle speed. The effective value of axle box transverse and vertical acceleration caused by wheel polygon increases with the increase of wave depth or polygon order; the analysis shows that the polygonal wear of the wheel has a great impact on the vibration characteristics of the axle box and can cause the high-frequency vibration of the axle box.
1. Introduction
Bogie is one of the main components to ensure the safe driving of rail vehicles. Its characteristics in the process of vehicle driving directly affect the operation safety and ride comfort of vehicles [1-3].
Due to the influence of various factors such as vehicle speed, track irregularity wavelength and so on when the train is running, the wear of the wheels during the running process will lead to the wheel polygonal changes of different orders, resulting in periodic wheel-rail excitation during the running of the train. Kaller analyzed the wheel rail contact theory, and discussed the application scope and limitations of different contact theories [4-5]; Jin et al., Ma et al. and Johansson et al. measured the wheel out of roundness on site and analyzed the formation mechanism of wheel polygon [6-10]; Song et al. and Liu and Zhai analyzed the relationship between the wheel polygon and the vertical dynamic action of wheel rail. The results show that the edge of wheel polygon will cause the high-frequency vibration of wheel set and rail [11-12].
In this paper, the vehicle track coupling dynamic model is established, and the vehicle dynamic simulation model is established by using SIMPACK. The influence of wheel polygon on the vibration characteristics of axle box and bogie frame is analyzed.
2. Vehicle dynamics model
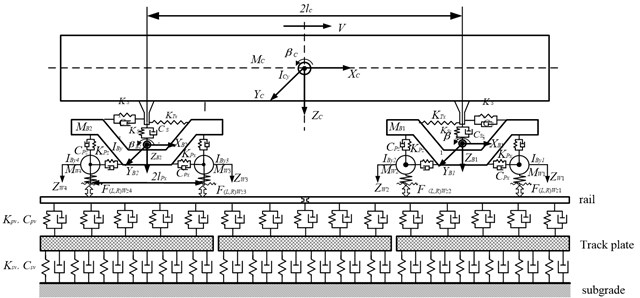
The vibration of axle box system caused by wheel tread damage during vehicle driving is mainly transmitted to the vehicle axle box system through wheel rail interaction. In this paper, the vehicle track coupling dynamic model is adopted in the analysis, as shown in Fig. 1. In the model, the vehicle system is simplified into one vehicle body, two frames and four wheel sets, in which the wheel sets consider four degrees of freedom: heave, traverse, roll and shake head, and the vehicle body and frame consider five degrees of freedom: heave, traverse rolling, shaking head and nodding. The primary spring, primary shock absorber, secondary air spring and anti snake shock absorber are simulated by spring damping system. The rail vibration is analyzed by Euler beam model. The contact between rail and wheel set is solved by Hertz nonlinear elastic contact theory. The vibration differential equation of rail is:
Fig. 1Vehicle track coupling dynamic model
3. Wheel polygon model
The formation of wheel polygon feature is mainly caused by the dynamic imbalance of brake wheel set and regular vibration and impact during wheel operation. For the simulation of wheel polygon, when only one order polygon is dominant in the wheel polygon, the wheel tread shape presents a regular polygon, and the wheel polygon can be represented by a single frequency simple harmonic; when the wheel is dominated by multiple order polygons, the wheel tread shape presents an irregular polygon. At this time, the wheel polygon needs to be represented by a simple harmonic function composed of multiple simple harmonic waves with different frequencies. For the vehicle system excitation caused by wheel polygon, the radial deviation of the wheel is generally expressed by a simple harmonic function of order 1-, and the expression equation is shown in Eq. (3):
where, is the radial deviation of wheel polygon, is the order of the wheel, is the harmonic amplitude of the -th order wheel polygon, is the nominal radius of the wheel, is the actual rolling radius of the wheel when turning , is the angular speed of wheel rotation.
During train operation, the vibration excitation frequency generated by wheel polygon is:
where, is the vibration frequency related to the wheel polygon, is the order of the wheel, is the wheel diameter.
4. Influence of wheel polygon on vibration characteristics of bogie system
In this paper, SIMPACK multi-body dynamics simulation software is used for simulation calculation. During the modeling process, the vehicle body, frame, wheel set, axle box, motor, gear box and other components in the vehicle system are regarded as rigid bodies, as shown in Fig. 2, the simulation dynamics model of the motor car is simulated and established in this paper. Abmp1, abmp2, abmp3 and abmp4 in Fig. 2(a) are the measuring points of the left axle box of the 1-position wheel set of the bogie, the measuring points of the right axle box of the 1-position wheel set of the bogie measuring points of left axle box of bogie 2-position wheel set and right axle box of bogie 2-position wheel set.
Fig. 2SIMPACK simulation model
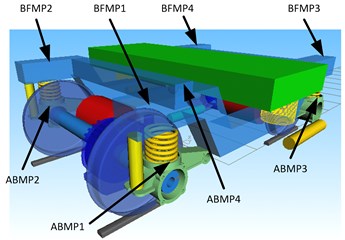
a) Motor car bogie model
b) Rail vehicle model
4.1. Influence of wheel polygon on transverse vibration characteristics of axle box system
During the simulation, the wheel polygon is set at the right wheel of the 2-position wheel set of the front bogie of the vehicle, and the other wheels of the vehicle are normal wheels.
Fig. 3(a) and Fig. 3(b) are the time domain and frequency domain results of lateral vibration acceleration of vehicle axle box under the excitation of wheel polygon order of 20 and amplitude of 0.15 mm when the simulation speed is 300 km/h; when the simulated speed is 300 km/h, it can be seen from the waveform diagram of axle box transverse vibration acceleration under wheel polygon excitation shown in Fig. 3(a) that the amplitude of axle box transverse acceleration on both sides of polygon wheel set is higher than that of normal wheel set.
Fig. 3Transverse vibration characteristics of axle box under wheel 20 edge excitation
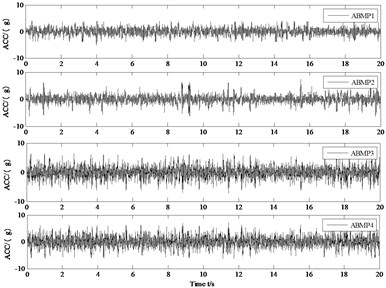
a) Time domain diagram
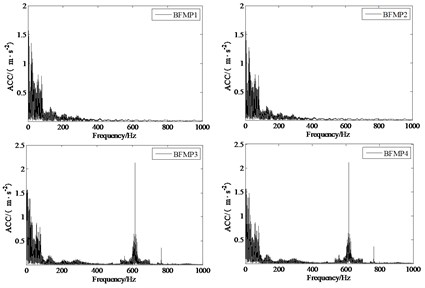
b) Frequency domain diagram
It can be seen from the statistical results in Table 1 that when the wheel set has polygonal wear, the effective value of the transverse acceleration of the axle box on both sides of the polygonal wheel set is greater than that of the axle box on both sides of the normal wheel set; it can be seen from the results that the effective value of the lateral acceleration of the right axle box of the 2-bit wheel set is 18.95 % higher than the average value of the effective value of the lateral acceleration of the axle box of the normal wheel set, and the effective value of the lateral acceleration of the left axle box of the 2-bit wheel set is 18.83 % higher than the average value of the effective value of the lateral acceleration of the axle box of the normal wheel set.
It can be seen from the spectrum diagram of axle box transverse vibration acceleration under polygonal excitation shown in Fig. 3(b) that the transverse vibration frequency of normal wheel set axle box is mainly distributed in 0-400 Hz, the amplitude of polygonal wheel set axle box transverse acceleration relative to normal wheel set axle box transverse acceleration increases significantly in 550-690 Hz frequency domain, and there is a peak at 616.9 Hz (20th order polygon). It can be seen that when the wheel is polygonal, it can cause the lateral vibration of axle box in the polygonal excitation frequency range of wheel.
Table 1Statistical table of axle box lateral acceleration under wheel 20 edge excitation
Position | Min (g) | Max (g) | RMS (g) |
ABMP1 | –7.2208 | 6.3392 | 1.2798 |
ABMP2 | –7.5024 | 6.6904 | 1.2826 |
ABMP3 | –7.5040 | 6.7752 | 1.5224 |
ABMP4 | –7.7888 | 7.0128 | 1.5240 |
4.2. Influence of wheel polygon on vertical vibration of vehicle axle box system
As shown in Fig. 4(a) the vertical vibration acceleration waveform of axle box under polygonal excitation of wheel is shown. It can be seen from the figure that the vertical acceleration amplitude of axle box on both sides of polygonal wheel set is significantly higher than that of normal wheel set. According to the statistical results in Table 2, the effective value of the vertical acceleration of the left axle box of the 2-bit wheel set is 54.80 % higher than the average value of the effective value of the vertical acceleration of the normal axle box, and the effective value of the vertical acceleration of the right axle box of the 2-bit wheel set is 246.04 % higher than the average value of the effective value of the vertical acceleration of the normal axle box.
Fig. 4Vertical vibration characteristics of axle box under wheel 20 edge excitation
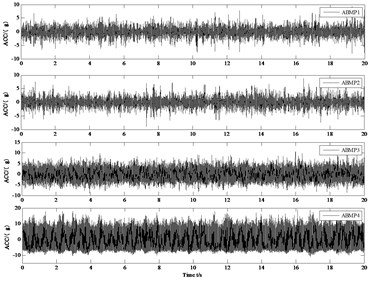
a) Time domain diagram
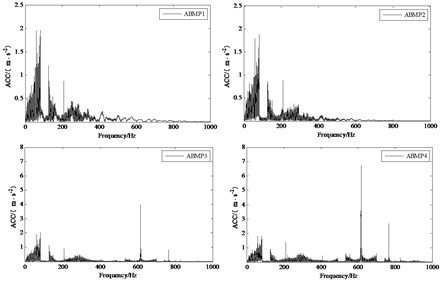
b) Frequency domain diagram
Table 2Statistics of vertical acceleration of axle box under wheel 20 edge excitation
Position | Min (g) | Max (g) | RMS (g) |
ABMP1 | –7.6370 | 7.8580 | 1.6340 |
ABMP2 | –9.0144 | 8.8020 | 1.6214 |
ABMP3 | –8.8855 | 9.8734 | 2.5196 |
ABMP4 | –10.8118 | 19.0699 | 5.6323 |
It can be seen from the spectrum of vertical vibration acceleration of axle box under polygonal excitation shown in Fig. 4(b) that the vertical vibration frequency of axle box of normal wheel set is mainly distributed at 0-400 Hz, and the vibration amplitude of vertical acceleration of axle box of polygonal wheel set is basically unchanged in the frequency domain range of 0-400 Hz relative to the vertical acceleration of axle box of normal wheel set, but the amplitude increases significantly in the frequency domain ranges of 534-690 Hz and 743.7-790 Hz, the peak value appears at 616.9 Hz (20th order polygon) and 766.07 Hz. It can be seen that when the wheel comes out of the polygon, it can cause the high-frequency vibration of the axle box in the vertical direction.
From the comparison of time domain curves of axle box transverse and vertical acceleration shown in Fig. 3(a) and Fig. 4(a), it can be seen that the vibration amplitude of axle box transverse acceleration is much lower than that of axle box vertical acceleration under the same wheel polygon excitation condition; when the wheel polygon appears, it will cause the high-frequency vibration of the axle box in the vertical and horizontal directions, and will have an impact on the axle box in the horizontal and vertical directions. The vertical impact of the axle box caused by the wheel polygon is more significant.
4.3. Influence of different wheel polygon parameters on vibration of axle box system
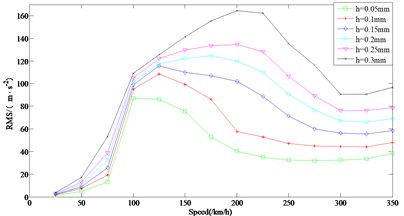
Through the statistics of the order of the real wheel polygon of the simulation example vehicle, it is found that the polytropic side of the wheel is dominated by the 20 order wheel polygon. Therefore, only the lateral and vertical vibration characteristics of the axle box under the excitation of the 20 order polygon at the speed of 25 km/h-350 km/h are simulated and analyzed. Fig. 5(a) and Fig. 5(b) are the characteristic laws of transverse and vertical vibration of axle box under 20 order polygon excitation at 25 km/h-350 km/h respectively. It can be seen from Fig. 5(a) that at the same speed, the effective value of axle box transverse vibration acceleration gradually increases with the increase of wheel polygon wave depth amplitude; it can be seen from the effective value curve of axle box transverse acceleration in the figure that the variation trend of axle box transverse vibration caused by different polygon wave depth amplitudes with vehicle speed is basically the same under the condition of 20th order polygon, with peak points near the vehicle speed of 125 km/h, and the effective value of axle box transverse acceleration increases rapidly in the range of 75 km/h-100 km/h; In the range of 200 km/h-300 km/h, the effective value of transverse vibration acceleration of axle box decreases gradually with the increase of vehicle speed.
Fig. 5Effective value curve of axle box acceleration under different 20th order polygonal wave depth amplitude excitation
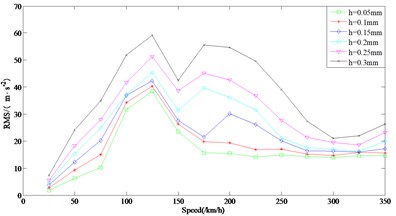
a) Transverse
b) Vertical
As can be seen from Fig. 5(b), when the amplitude of polygonal wave depth is in the range of 0.05 mm-0.3 mm and the vehicle speed is the same, the effective value of vertical vibration acceleration of axle box gradually increases with the increase of amplitude of polygonal wave depth of wheel. According to the effective value curve of axle box vertical acceleration in the figure, the variation trend of axle box vertical vibration caused by different polygonal wave depth amplitudes with vehicle speed is basically the same, showing a trend of first increasing, then decreasing and then increasing. When the vehicle speed is near 300 km/h, the effective value curve of axle box vertical acceleration appears trough point; the effective value of vertical acceleration of axle box caused by polygons with different amplitudes in the interval of 25 km/h-125 km/h is basically similar, and the effective value of vertical acceleration of axle box increases rapidly in the interval of 75 km/h-100 km/h. The variation characteristics of vertical acceleration of axle box in this speed section are the same as those of transverse acceleration of axle box. Under the excitation of the 20th order polygonal wheel, the vehicle speed corresponding to the peak value of the effective value of the vertical acceleration of the axle box increases with the increase of the amplitude of the polygonal wave depth.
Fig. 6V= 300 km/h axle box acceleration RMS
a) Transverse
b) Vertical
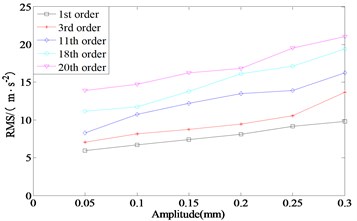
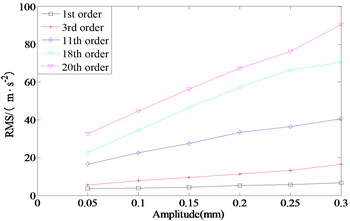
Fig. 6(a) and Fig. 6(b) show the influence law of different wave depth amplitudes of 1st, 3rd, 11th, 18th and 20th order polygons on the vibration acceleration of axle box at the speed of 300 km/h. It can be seen from Fig. 6(a) that under the same vehicle speed, with the increase of wave depth, the effective value of axle box transverse acceleration caused by wheel polygons of different orders shows an increasing trend, and the change rate of effective value of axle box transverse acceleration with the amplitude of wave depth under the five-wheel polygon states is not different.
It can be seen from Fig. 6(b) that under the same vehicle speed, with the increase of wave depth, the effective value of axle box vertical acceleration caused by wheel polygon shows an increasing trend. Under the five-wheel polygon states, the change rate of effective value of axle box vertical acceleration with the amplitude of wave depth gradually increases with the increase of polygon order.
5. Conclusions
1) At the same speed, with the increase of the wave depth of the wheel polygon, the effective values of the transverse and vertical acceleration of the axle box gradually increase; the effective value of axle box vertical vibration acceleration caused by wheel polygons with different amplitudes increases first, then decreases and then increases with the change of vehicle speed.
2) At the same speed, the effective values of transverse and vertical acceleration of axle box caused by wheel polygon increase with the increase of wave depth or polygon order.
3) The analysis shows that the polygonal wear of the wheel has a great impact on the vibration characteristics of the axle box and can cause the high-frequency vibration of the axle box.
References
-
H. L. Shi, P. B. Wu, J. Zeng, and D. F. Zhang, “Flexibility characteristics of suspension system for railway vehicle,” Journal of Traffic and Transportation Engineering, Vol. 14, No. 4, pp. 45–52, 2014.
-
F. Li, M. H. Fu, Y. H. Huang, and W. B. Ni, “Research on car air spring dynamics parameter traits,” China Railway Science, Vol. 24, No. 5, pp. 91–95, 2003.
-
H. Y. Liu, “Study on key dynamics problems of high-speed train,” China Railway Science, Vol. 25, No. 1, pp. 136–138, 2004.
-
J. J. Kalker, “Survey of wheel-rail rolling contact theory,” Vehicle System Dynamics, Vol. 8, No. 4, pp. 317–358, Sep. 1979, https://doi.org/10.1080/00423117908968610
-
B. Jacobson and J. J. Kalker, “Rolling contact phenomena,” in CISM International Centre for Mechanical Sciences, Vienna: Springer Vienna, 2000, https://doi.org/10.1007/978-3-7091-2782-7
-
X. Jin, L. Wu, J. Fang, S. Zhong, and L. Ling, “An investigation into the mechanism of the polygonal wear of metro train wheels and its effect on the dynamic behaviour of a wheel/rail system,” Vehicle System Dynamics, Vol. 50, No. 12, pp. 1817–1834, Dec. 2012, https://doi.org/10.1080/00423114.2012.695022
-
W. H. Ma, S. H. Luo, and R. R. Song, “Analyses of the form reason of wheel polygonization of subway vehicle,” Journal of Mechanical Engineering, Vol. 48, No. 24, pp. 106–111, 2012.
-
A. Johansson and J. C. O. Nielsen, “Out-of-round railway wheels-wheel-rail contact forces and track response derived from field tests and numerical simulations,” Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, Vol. 217, No. 2, pp. 135–146, Mar. 2003, https://doi.org/10.1243/095440903765762878
-
A. Johansson and C. Andersson, “Out-of-round railway wheels-a study of wheel polygonalization through simulation of three-dimensional wheel-rail interaction and wear,” Vehicle System Dynamics, Vol. 43, No. 8, pp. 539–559, Aug. 2005, https://doi.org/10.1080/00423110500184649
-
A. Johansson, “Out-of-round railway wheels-assessment of wheel tread irregularities in train traffic,” Journal of Sound and Vibration, Vol. 293, No. 3-5, pp. 795–806, Jun. 2006, https://doi.org/10.1016/j.jsv.2005.08.048
-
Y. Song, Z. Wang, and Y. Shen, “Research on the control of out-of-round wheel profiles of high-speed railway derived from numerical simulations,” International Journal of Online Engineering, Vol. 9, No. 6, pp. 92–95, 2013.
-
X. Liu and W. Zhai, “Analysis of vertical dynamic wheel/rail interaction caused by polygonal wheels on high-speed trains,” Wear, Vol. 314, No. 1-2, pp. 282–290, Jun. 2014, https://doi.org/10.1016/j.wear.2013.11.048
Cited by
About this article
Z. Niu would like to express appreciation to Professor Su Jian and Dr. Yirui Zhang for valuable discussions that improved the quality and presentation of the paper.
