Constraint following control for unmanned combat platforms based on robot formation systems

Zhu, Song Bai; Yang, Guo Lai

doi:10.21595/vp.2022.22837

Vibroengineering Procedia

Browse Procedia

Published: 25 August 2022

Check for updates

Constraint following control for unmanned combat platforms based on robot formation systems

Song Bai Zhu¹

Guo Lai Yang²

^{1, 2}School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing, 210094, Jiangsu, China

Corresponding Author:

Guo Lai Yang

Cite the article Download PDF

Downloads 322

CrossRef Citations 1

Abstract

With advances in robotics and communications engineering, robots are replacing humans in a variety of jobs. In military applications, the control problem of the robot formation, a major part of unmanned combat platforms, has also become a focus of research. This paper proposes constrained following control to solve the problem of collision avoidance, following and reaching in robot formation systems. First, the state space equations of robot formations are established based on the U-K theory. Second, the collision avoidance following constraint of the system is transformed into an approximate following constraint, and the constrained following error is established. The arrival constraint is added to provide the destination of the formation. Third, the adaptive robust controller is proposed to solve the potential complex uncertainty interference of systems. Uniformly bounded and uniformly ultimately bounded of the constraint following error are guaranteed. Finally, the effectiveness of the controller is verified by simulation experiments.

1. Introduction

Unmanned combat platforms are a class of robotic systems carrying weapons for combat missions that can be controlled by pre-programmed or operated remotely [1]. It reduces casualties and improves combat efficiency through its high mobility, low cost, difficult detection, and long endurance. As one of the main directions for building intelligent weapons platforms, it has become a popular research topic for all major military powers. To improve the efficiency of unmanned combat platforms in battlefield material transportation, reconnaissance, personnel search and rescue, and field operations, an unmanned combat formation platform based on robot formation is proposed. In recent years, several scholars have proposed methods to address the following control [2] and avoidance control [3] of robot formations on the battlefield. However, they ignore the simultaneous nature of following and avoidance in actual combat. In other words, the robots in the formation are required to perform target tracking while keeping the distance between robots within a safe range. The difficulty of the following and avoidance control of robot formations increases due to the complex uncertainty in the battlefield environment.

In the study of control of uncertain systems, Udwadia and Kalaba proposed a control strategy for uncertain mechanical systems. Chen [4] categorized the traditional stability control, trajectory tracking control and optimization control as servo-constrained control based on U-K theory, and applied constrained following control to these situations. Xu [5] applied constraint following control to fuzzy mechanical systems, proposed an index considering control cost and effectiveness, and transformed the gain design of the adaptive method into a constrained optimization problem.

The above study shows the applicability of approximate constraint following methods for the control of uncertain mechanical systems. This paper converts the collision avoidance, following, and arrival control of the robot formation system into an approximate constrained following problem. By designing an adaptive robust control, the constrained following error of the system can be uniformly bounded and uniformly ultimately bounded under the complex uncertainty. The robot formations can achieve the expected performance and have been verified by simulation experiments.

2. Modeling of constrained mechanical systems with uncertainty

An $n$ -dimensional mechanical system can be described as [6]:

1

M (q (t), σ (t), t) \ddot{q} (t) + C (q (t), \dot{q} (t), σ (t), t) \dot{q} + G (q (t), σ (t), t) + f (q (t), \dot{q} (t), σ (t), t) = τ (t),

where $t \in R$ is the time, $q \in R^{n}$ is the displacement, $\ddot{q} \in R^{n}$ is the velocity, $\dot{q} \in R^{n}$ is the acceleration respectively. $τ \in R^{n}$ is the control input. $σ$ is uncertain of the system. $Σ \in R^{p}$ is compact but unknown, and $σ \in Σ \in R^{p}$ . $M (\cdot) > 0$ is the inertia matrix, $C (\cdot)$ is the Coriolis/centrifugal force matrix, $G (\cdot)$ is the gravitational force and $f (\cdot)$ are other interfering forces.

Considering the constraint equations followed by the system, the first-order form is:

2

\sum_{i = 1}^{n} A_{m i} (q, t) {\dot{q}}_{i} (t) = c_{m} (q, t), m = 1, \dots, k .

where $m \leq k \leq n$ , ${\dot{q}}_{i} (t)$ . is the $i$ th component of $\dot{q} (t)$ . Assuming $A = {[A_{m}]}_{k \times n}$ , $c = {[c_{1} c_{2} \dots c_{k}]}^{T}$ , then:

3

A (q, t) \dot{q} (t) = c (q, t) .

The second-order derivative of Eq. (2) with respect to $t$ is:

4

\sum_{i = 1}^{n} A_{m i} (q, t) {\ddot{q}}_{i} (t) = - \sum_{i = 1}^{n} \frac{d A_{m i} (q, t)}{d t} {\dot{q}}_{i} (t) + \frac{d c_{m} (q, t)}{d t} = : b_{m} (\dot{q}, q, t), m = 1, \dots, k .

Similarly, let $b = {[b_{1}, b_{2} \dots b_{k}]}^{T}$ , we have:

5

A (q, t) \ddot{q} = b (\dot{q}, q, t) .

Then, the constraint following error is defined as:

6

β (\dot{q}, q, t) = A (q (t), t) \dot{q} (t) - c (q (t), t) .

Therefore, the control objective changes from $q \to q_{d}$ , $\dot{q} \to {\dot{q}}_{d}$ to $β \to 0$ by constraint following analysis.

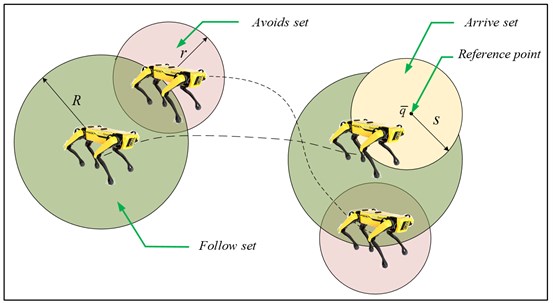
Considering the distance relationship between robots in the formation:

7

d_{q} (t) = {‖q (t)‖}^{2} .

The following sets are defined to guarantee collision avoidance and following performance of the robot:

8

Ψ = \{q_{m} \in R^{n_{m}} ∣ r^{2} < d_{q} (t) < R^{2}\},

where $r$ , $R \in R_{+}$ represent the following-signal transmission radius and the safety distance between robots, respectively. Defining:

9

e_{1} (t) : = l n [(R^{2} - d_{q}) (d_{q} - r^{2})] .

Taking the first derivative of $t$ :

10

{\dot{e}}_{1} = \frac{R^{2} + r^{2} - 2 d_{q}}{(R^{2} - d_{q}) (d_{q} - r^{2})} \sum_{i = 1}^{m} \frac{\partial d_{q}}{\partial q_{i}} {\dot{q}}_{i} = \frac{R^{2} + r^{2} - 2 d_{q}}{(R^{2} - d_{q}) (d_{q} - r^{2})} \frac{\partial d_{q}}{\partial q} \dot{q} .

Considering Eq. (6), let:

11

β_{1} : = {\dot{e}}_{1} = \frac{R^{2} + r^{2} - 2 d}{(R^{2} - d_{q}) (d_{q} - r^{2})} \frac{\partial d_{q}}{\partial q} \dot{q} .

For this typical control following system, defining the following error is:

12

e_{2} (t) : = ‖q (t) - q_{0}‖ - s = Q (q (t)) - s,

where $s$ , $q_{0}$ are the radius and the circle center of the arrival area. Differentiating Eq. (12) with respect to $t$ yields:

13

{\dot{e}}_{2} = \frac{\partial Q (q (t))}{\partial q} \dot{q} (t) .

According to equation Eq. (6), let:

14

β_{2} (q, \dot{q}) = {\dot{e}}_{2} + l e_{2} = \frac{\partial Q (q (t))}{\partial q} \dot{q} (t) + l Q (q (t)) - l s = A_{2} (q (t)) \dot{q} (t) - c_{2} (q (t)),

where $l$ is a constant.

With the above analysis, the original constraints on collision avoidance, following and arrival in the system are transformed into approximate following constraints.

3. Adaptive robust control design

The matrix of Eq. (1) is decomposed to express the uncertainty explicitly:

15

\begin{array}{l} M (q, σ, t) = \bar{M} (q, t) + Δ M (q, σ, t), C (q, \dot{q}, σ, t) = \bar{C} (q, \dot{q}, t) + Δ C (q, \dot{q}, σ, t), \\ g (q, σ, t) = \bar{g} (q, t) + Δ g (q, σ, t), f (q, σ, t) = \bar{f} (q, t) + Δ f (q, σ, t) . \end{array}

For later analysis, let $B : = {\bar{M}}^{- 1}$ , $H : = \bar{M} M^{- 1} - I$ , and $Δ B : = M^{- 1} - {\bar{M}}^{- 1} = B H$ . Let:

16

p_{1} (q, \dot{q}, t) : = {\bar{M}}^{\frac{1}{2}} {(A {\bar{M}}^{- \frac{1}{2}})}^{+} [b + A M^{- 1} (\bar{C} \dot{q} + \bar{g} + \bar{f})],

17

p_{2} (q, \dot{q}, t) : = - κ \bar{M} A^{T} {(A A^{T})}^{- 1} β .

$p_{1}$ is used to control the deterministic part of the system to approach the constrained. $p_{2}$ is used to enable the system close to the constrained quickly. Continued design is necessary to overcome the uncertainty of the system.

Assumption 1: (1) For each $(q, \dot{q}, t) \in R^{n} \times R^{n} \times R α_{1,2} \in {(0, \infty)}^{k}$ , the function $ϕ (α, q, \dot{q}, t) : (0, \infty)^{k} \to R_{+}$ meets:

18

ϕ (α_{1}, q, \dot{q}, t) - ϕ (α_{2}, q, \dot{q}, t) \leq \frac{\partial ϕ}{\partial α} (α_{2}, q, \dot{q}, t) (α_{1} - α_{2}),

and (iii) non-decreasing with respect to each component of its argument $α$ . $ϕ (α, q, \dot{q}, t)$ can be linearly factorized with respect to $α$ , we have:

19

ϕ (α, q, \dot{q}, t) = α^{T} \hat{ϕ} (q, \dot{q}, t) .

Recalling Eq. (6), the adaptive law is proposed:

20

\dot{\hat{α}} = k_{1} \frac{\partial ϕ^{T}}{\partial α} (\hat{α}, q, \dot{q}, t) ‖β‖ - k_{2} \hat{α},

where $\hat{α} (0) > 0$ , $k_{1,2} \in R_{+}$ is adaptive design parameters. An adaptive control term is defined as follows:

21

p_{3} (α, β, q, \dot{q}, t) = - γ [\bar{M} A^{T} {(A A^{T})}^{- 1}] β ϕ^{2},

where:

22

γ = \{\begin{array}{l} 1 / β ϕ, β ϕ > λ, \\ 1 / λ, β ϕ \leq λ . \end{array}

And $λ > 0$ is a scalar constant. Let the system control input $τ$ as:

23

τ (t) = p_{1} (q, \dot{q}, t) + p_{2} (q, \dot{q}, t) + p_{3} (α, β, q, \dot{q}, t) .

4. Simulations

Fig. 1 presents the robot formation system, its state space equation can be expressed as:

24

[\begin{matrix} m_{1} & 0 \\ 0 & m_{1} \end{matrix}] [\begin{array}{l} {\ddot{x}}_{1} \\ {\ddot{y}}_{1} \end{array}] + [\begin{array}{l} C_{1 x} \\ C_{1 y} \end{array}] [\begin{array}{l} {\dot{x}}_{1} \\ {\dot{y}}_{1} \end{array}] + [\begin{array}{l} f_{1 x} \\ f_{1 y} \end{array}] = [\begin{array}{l} τ_{1 x} \\ τ_{1 y} \end{array}],

[\begin{matrix} m_{2} & 0 \\ 0 & m_{2} \end{matrix}] [\begin{array}{l} {\ddot{x}}_{2} \\ {\ddot{y}}_{2} \end{array}] + [\begin{array}{l} C_{2 x} \\ C_{2 y} \end{array}] [\begin{array}{l} {\dot{x}}_{2} \\ {\dot{y}}_{2} \end{array}] + [\begin{array}{l} f_{2 x} \\ f_{2 y} \end{array}] = [\begin{array}{l} τ_{2 x} \\ τ_{2 y} \end{array}] .

According to the design objective, the distance between two robots should satisfy the following conditions:

25

r^{2} < (x_{1} - x_{2})^{2} + (y_{1} - y_{2})^{2} < R^{2} .

Recalling Eq. (7), let $d_{q} = (x_{1} - x_{2})^{2} + (y_{1} - y_{2})^{2}$ . Taking it to Eq. (9):

26

{\dot{e}}_{1} = \frac{2 \{R^{2} + r^{2} - 2 d (x, y)\}}{(R^{2} - d_{q}) (d_{q} - r^{2})} {[\begin{array}{l} x_{1} - x_{2} \\ y_{1} - y_{2} \\ x_{2} - x_{1} \\ y_{2} - y_{1} \end{array}]}^{T} ⌊\begin{array}{l} {\dot{x}}_{1} \\ {\dot{y}}_{1} \\ {\dot{x}}_{1} \\ {\dot{y}}_{2} \end{array}⌋ = A_{1} \dot{q} - c_{1} .

Taking the second derivative of time:

27

{\ddot{e}}_{1} = \frac{2 \{R^{2} + r^{2} - 2 d_{q}\}}{(R^{2} - d_{q}) (d_{q} - r^{2})} {[\begin{array}{l} x_{1} - x_{2} \\ y_{1} - y_{2} \\ x_{2} - x_{1} \\ y_{2} - y_{1} \end{array}]}^{T} ⌊\begin{array}{l} {\ddot{x}}_{1} \\ {\ddot{y}}_{1} \\ {\ddot{x}}_{1} \\ {\ddot{y}}_{2} \end{array}⌋ + \frac{2 \{R^{2} + r^{2} - 2 d_{q}\} (({\dot{x}}_{1} - {\dot{x}}_{2})^{2} + ({\dot{y}}_{1} - {\dot{y}}_{2})^{2})}{(R^{2} - d_{q}) (d_{q} - r^{2})}

- \frac{8 (R^{2} - d_{q}) (d_{q} - r^{2}) + 4 {(R^{2} + r^{2} - 2 d_{q})}^{2}}{(R^{2} - d_{q}) {(d_{q} - r^{2})}^{2}} {[(x_{1} - x_{2}) ({\dot{x}}_{1} - {\dot{x}}_{2}) + (y_{1} - y_{2}) ({\dot{y}}_{1} - {\dot{y}}_{2})]}^{2} = A_{1} \ddot{q} - b_{1} .

Fig. 1Diagram of robot formation

Considering arrival constraints, let $Q (x, y) = (x - \bar{x})^{2} + (y - \bar{y})^{2}$ , combining Eqs. (12) and (13) we obtain:

28

{\dot{e}}_{2} = {[\begin{matrix} 2 (x_{1} - {\bar{x}}_{1}) \\ 2 (y_{1} - {\bar{y}}_{1}) \\ 0 \\ 0 \end{matrix}]}^{T} [\begin{array}{l} {\dot{x}}_{1} \\ {\dot{y}}_{1} \\ {\dot{x}}_{2} \\ {\dot{y}}_{2} \end{array}] + l_{1} {(x_{1} - {\bar{x}}_{1})}^{2} + l_{1} {(y_{1} - {\bar{y}}_{1})}^{2} - l_{1} s_{1}^{2} = : A_{2} \dot{q} - c_{2},

29

{\dot{e}}_{3} = {[\begin{matrix} 0 \\ 0 \\ 2 (x_{2} - x_{1}) \\ 2 (y_{2} - y_{1}) \end{matrix}]}^{T} [\begin{array}{l} {\dot{x}}_{1} \\ {\dot{y}}_{1} \\ {\dot{x}}_{2} \\ {\dot{y}}_{2} \end{array}] + l_{2} {(x_{2} - {\bar{x}}_{2})}^{2} + l_{2} {(y_{2} - {\bar{y}}_{2})}^{2} - l_{2} r_{2}^{2} = : A_{3} \dot{q} - c_{3} .

The derivative of the time for Eqs. (28) and (29) yields:

30

{\ddot{e}}_{3} = {[\begin{matrix} 2 (x_{1} - {\bar{x}}_{1}) \\ 2 (y_{1} - {\bar{y}}_{1}) \\ 0 \\ 0 \end{matrix}]}^{T} [\begin{array}{l} {\ddot{x}}_{1} \\ {\ddot{y}}_{1} \\ {\ddot{x}}_{2} \\ {\ddot{y}}_{2} \end{array}] + 2 {\dot{x}}_{1}^{2} + 2 {\dot{y}}_{1}^{2} + 2 l_{1} (x_{1} - {\bar{x}}_{1}) {\dot{x}}_{1} + 2 l_{1} (y_{1} - {\bar{y}}_{1}) {\dot{y}}_{1} = : A_{2} \ddot{q} - b_{2},

31

{\ddot{e}}_{3} = {[\begin{matrix} 0 \\ 0 \\ 2 (x_{2} - x_{1}) \\ 2 (y_{2} - y_{1}) \end{matrix}]}^{T} [\begin{array}{l} {\ddot{x}}_{1} \\ {\ddot{y}}_{1} \\ {\ddot{x}}_{2} \\ {\ddot{y}}_{2} \end{array}] + 2 {\dot{x}}_{2}^{2} + 2 {\dot{y}}_{2}^{2} + 2 l_{2} (x_{2} - {\bar{x}}_{2}) {\dot{x}}_{2} + 2 l_{2} (y_{2} - y_{1}) {\dot{y}}_{2} = : A_{3} \ddot{q} - b_{3} .

According to Eqs. (26)-(31), we can obtain $A = {[\begin{array}{l} A_{1} & A_{2} & A_{3} \end{array}]}^{T}$ , $c = {[\begin{array}{l} c_{1} & c_{2} & c_{3} \end{array}]}^{T}$ , $b = {[\begin{array}{l} b_{1} & b_{2} & b_{3} \end{array}]}^{T} .$

Some structural parameters of the system are given:

\bar{f} = 0, Δ f = 0.2 s i n (5 t), m_{1,2} = 20, R = 4, r = 1, l_{1,2} = 0.5, s_{1,2} = 0.5,

C_{k} = 1.1, x_{1} (0) = 1, y_{1} (0) = 5, {\dot{x}}_{1} (0) = 1, {\dot{y}}_{1} (0) = 1,

{\bar{x}}_{1} = 4, {\bar{y}}_{1} = 2, x_{2} (0) = 2, y_{2} (0) = 2, {\dot{x}}_{2} (0) = 0.5, {\dot{y}}_{2} (0) = 1

, {\bar{x}}_{2} = 4, {\bar{y}}_{2} = 3, k_{1} = 1, k_{2} = 0.3, κ = 50, ε = 0.1, \hat{α} (0) = 5 .

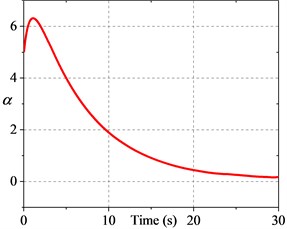
Fig. 2 presents the errors of the system and they converge to zero after a period of time. Fig. 3 illustrates that the distance between robots is difficult to maintain within the desired range when collision avoidance and following constraints are not considered. Fig. 4 shows the variation of the adaptation parameter.

Fig. 2History of constraint-following error β

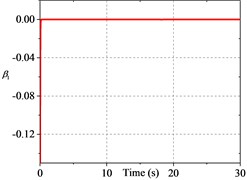
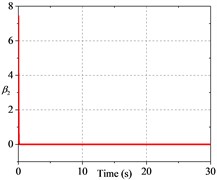
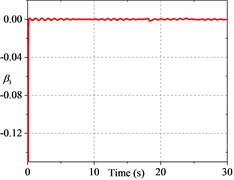
Fig. 3Performance comparison

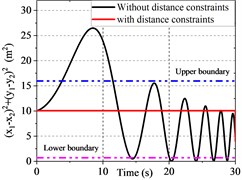
a) Distance between robots

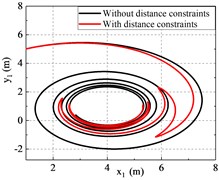
b) Trajectory of robot 1

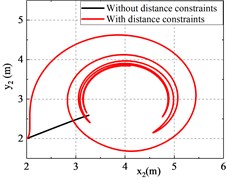
c) Trajectory of robot 2

Fig. 4History of the adaptive parameter

5. Conclusions

This paper presents the collision-following-arrival problem for an unmanned combat platform system based on robot formations. The original constraint is transformed into an approximate following constraint. After that, adaptive robust controllers are designed to cope with the complex uncertainties in the system and drive the system to achieve the desired performance. The main contributions of this paper are the following three points: (1) a more practical formation control problem is proposed by combining the collision avoidance, following and arrival problems of uncertain robot formation systems; (2) an adaptive robust control method is proposed to solve the impact of complex uncertainties on unmanned combat platforms on the battlefield and improve the stability of platform operation; (3) a theoretical reference is provided for robot formation control.

References

D. Shen et al., “An orbital emulator for pursuit-evasion game theoretic sensor management,” in SPIE Defense + Security, Vol. 10196, pp. 122–131, May 2017, https://doi.org/10.1117/12.2266606

Publisher
S. A. Ajwad, E. Moulay, M. Defoort, T. Menard, and P. Coirault, “Collision-free formation tracking of multi-agent systems under communication constraints,” 2021 American Control Conference (ACC), Vol. 5, No. 4, pp. 1345–1350, May 2021, https://doi.org/10.23919/acc50511.2021.9482618

Publisher
D. Shen, K. Pham, E. Blasch, H. Chen, and G. Chen, “Pursuit-evasion orbital game for satellite interception and collision avoidance,” in SPIE Defense, Security, and Sensing, Vol. 8044, No. 7, pp. 284–287, May 2011, https://doi.org/10.1117/12.882903

Publisher
Y.-H. Chen, “Constraint-following servo control design for mechanical systems,” Journal of Vibration and Control, Vol. 15, No. 3, pp. 369–389, Mar. 2009, https://doi.org/10.1177/1077546307086895

Publisher
J. Xu, Y.-H. Chen, and H. Guo, “A new approach to control design for constraint-following for fuzzy mechanical systems,” Journal of Optimization Theory and Applications, Vol. 165, No. 3, pp. 1022–1049, Jun. 2015, https://doi.org/10.1007/s10957-014-0604-9

Publisher
R. M. Rosenberg and W. E. Schmitendorf, “Analytical dynamics of discrete systems,” Journal of Applied Mechanics, Vol. 45, No. 1, pp. 233–234, Mar. 1978, https://doi.org/10.1115/1.3424263

Publisher

Cited by

Adaptive robust control for unmanned combat platform: Obstacles avoiding and dynamic trajectory tracking

Qinqin Sun | Yu Chen | Xiuye Wang | Yinlong Wang

(2024)

About this article

Received

19 July 2022

Accepted

05 August 2022

Published

25 August 2022

SUBJECTS

Vibration control, generation and harvesting

DOI

https://doi.org/10.21595/vp.2022.22837

Keywords

nonlinear dynamical systems

robot formation systems

adaptive robust control

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 01 08

Adaptive neural network vibration suppression control of flexible joints space manipulator based on H∞ theory

Zhangping You, Wenhui Zhang, Jinmiao Shen, Yangfan Ye, Xiaoping Ye, Shuhua Zhou

Research article

2021 12 02

Adaptive robust control for electric cylinder with friction compensation by LuGre model

Darui Lin, Guolai Yang

Research article

2021 08 11

Optimization of trajectory tracking control of 3-DOF translational robot use PSO method based on inverse dynamics control for surgery application

Ngoc Pham Van Bach, Quan Dam Hai, Thanh Bui Trung

Research article

2021 04 07

Adaptive fuzzy control of nonlinear aeroelastic system with measurement noise

Bo Zhang, Jinglong Han, Ruiqun Ma

S. B. Zhu and G. L. Yang, “Constraint following control for unmanned combat platforms based on robot formation systems,” Vibroengineering PROCEDIA, Vol. 44, pp. 40–46, Aug. 2022, https://doi.org/10.21595/vp.2022.22837

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2022.22837
UR  - https://doi.org/10.21595/vp.2022.22837
TI  - Constraint following control for unmanned combat platforms based on robot formation systems
T2  - Vibroengineering PROCEDIA
AU  - Zhu, Song Bai
AU  - Yang, Guo Lai
PY  - 2022
DA  - 2022/08/25
PB  - JVE International Ltd.
SP  - 40-46
VL  - 44
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Zhu_2022,
	doi = {10.21595/vp.2022.22837},
	url = {https://doi.org/10.21595/vp.2022.22837},
	year = 2022,
	month = {aug},
	publisher = {{JVE} International Ltd.},
	volume = {44},
	pages = {40--46},
	author = {Song Bai Zhu and Guo Lai Yang},
	title = {Constraint following control for unmanned combat platforms based on robot formation systems},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]S. B. Zhu and G. L. Yang, “Constraint following control for unmanned combat platforms based on robot formation systems,” Vibroengineering PROCEDIA, vol. 44, pp. 40–46, Aug. 2022, doi: 10.21595/vp.2022.22837.

Copy IEEE

Copied to clipboard!

Zhu, Song Bai, and Guo Lai Yang. “Constraint Following Control for Unmanned Combat Platforms Based on Robot Formation Systems.” Vibroengineering PROCEDIA 44 (August 25, 2022): 40–46. https://doi.org/10.21595/vp.2022.22837.

Copy Chicago

Copied to clipboard!

Constraint following control for unmanned combat platforms based on robot formation systems

Abstract

1. Introduction

2. Modeling of constrained mechanical systems with uncertainty

3. Adaptive robust control design

4. Simulations

5. Conclusions

References

Cited by

About this article

Related Articles