Adaptive neural network vibration suppression control of flexible joints space manipulator based on H∞ theory

1. Introduction

With the development of space technology, the research of space robot technology has been widely valued by scholars all over the world [1-3]. However, most of the research is based on the dynamics research and control algorithm design of space rigid body manipulator, that is, the space base, manipulator and joint are regarded as multi rigid body dynamic system, ignoring the influence of joint flexibility [4-5]. In fact, there is no absolute rigid connection between each manipulator joint of the robot and the driving motor at the base joint, due to the existence of the reducer, there is a certain flexibility between them. The advantage of the mechanical arm with this flexible joint is that it can absorb the impact force generated by external accidental collision and reduce the damage to the mechanical arm [6], but the disadvantage is that the damping delay in the movement process will cause the movement angle of the mechanical arm to no longer be consistent with the movement angle of the driving motor rotor, resulting in error, Its error accumulation will have an impact on the high-precision operation of space robot. Moreover, the joint flexibility of the manipulator will cause vibration in the process of motion at high speed [7-9].

International scholars have made a lot of useful discussions on the control of space robots with external disturbance, and have achieved some research results. [10-13] proposed their own adaptive control methods and designed adaptive learning laws to deal with the parameter uncertainties and changes of the dynamic model. However, the research objects of these achievements are rigid joint robot systems, rather than flexible joints. In fact, for space robots, the material of their manipulator is mainly carbon fiber composite, which is different from the cast iron manipulator of ground robots. Moreover, the transmission mechanism at the joint of the manipulator makes the joint show stronger flexibility, which can absorb energy in the process of collision and avoid damaging the actuator. However, the existence of joint flexibility makes a certain angle error between the rotation angle of the joint link and the motor rotor. If it is not compensated, it will seriously affect the tracking accuracy [14-16]. Moreover, joint flexibility will also lead to the elastic vibration of the manipulator, which will seriously affect the high-precision control of the manipulator [17-19].

In recent years, with the rapid development of space robots, the control of flexible manipulator has gradually attracted the attention of international scholars. Jiang et al. [20] proposed a neural network control method based on velocity feedback for a space manipulator considering joint flexibility. The experimental simulation verified the effectiveness of the control system. Akiko et al. [13] proposed a robust vibration suppression control method to solve the elastic vibration in the control process. Kawai et al. [21] proposed a hybrid control method based on dynamic boundary, which suppresses external disturbance through adaptive adjustment of the boundary. Experiments verify the effectiveness of the control method. Most of the above research is aimed at the control of flexible joint robot with fixed base on the ground, which provides a reference for the vibration suppression control of space manipulator with flexible joints.

Based on the above research, a robust control method based on adaptive neural network is proposed, taking into account the uncertainties such as external disturbance and joint flexibility in engineering practice. The purpose of the controller is to make the actual trajectory track the desired trajectory, compensate the error model caused by uncertain factors, and suppress the elastic vibration caused by joint flexibility. The main technical contributions of the proposed method are summarized below.

Based on the above research, this paper proposes an adaptive neural network control method based on H_∞ robust. The main technical contributions of the proposed method are summarized as follows.

1) Compared with the traditional dynamic model of space robot, the dynamic model of free- floating space robot with flexible joints is established by considering the unknown uncertainties caused by model inaccuracy, external disturbance and joint flexibility. It is more in line with the actual situation of the project.

2) A neural network robust controller based on H_∞ theory is designed. The unknown uncertain model is compensated by neural network, and the robust controller eliminates external disturbance and approximation error. An adaptive learning speed law of neural network weights is designed to realize online real-time adjustment.

3) A feedback compensation controller based on speed differential difference is designed to eliminate the angle error of joint angle and motor rotor, and then suppress the elastic vibration. The feedback algorithm is relatively simple, with small amount of calculation and high real-time performance, which is conducive to the rapid suppression of elastic vibration.

2. Dynamic modeling of space manipulator with flexible joints

The structure of free-floating planar two link space manipulators with flexible joints is established [22, 23], the model is shown in Fig. 1.

Fig. 1Free-floating space robot system with flexible joints

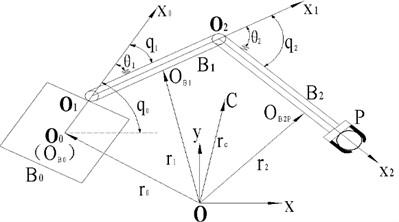
It can be seen from Fig. 1 that its position vector can be expressed as follows:

where $L_{0j}$, $L_{1j}$, $L_{2j}$ are the intermediate variable function, respectively.

Based on Spong model [24], we can get that its joints can be simplified as a linear torsion spring without inertia, as is shown in Fig. 2.

Fig. 2Flexible joint model

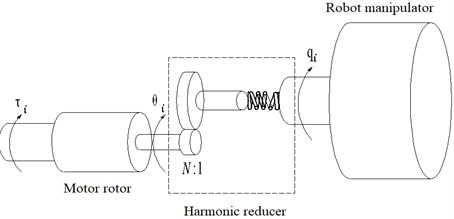
According to the Fig.1. above, due to the existence of flexible springs and other factors, the rotor of the joint motor turns ${\theta }_i$, rotation angle of manipulator rod $q_i$, here ${\theta }_i\ne q_i$. This will result in a continuous accumulation of errors, which will affect the final control accuracy. Based on Lagrange method in theoretical mechanics, the dynamic equation of industrial mechanical manipulator [25-28] can be derived:

where $\theta =[\begin{array}{ll}{\theta }_1& {\theta }_2\end{array}{]}^T$, $q=[\begin{array}{ll}{q}_1& q_2\end{array}{]}^T$, $J_{\theta }=diag(J_{\theta 1},J_{\theta 2})\in {\mathbb{R}}^{2\times 2}$ is the diagonally Positive definite matrix of the motor, $D\left(q\right)\in {\mathbb{R}}^{2\times 2}$ is the symmetric positive definite matrix of the manipulator, $H(q,\dot{q},\dot{\theta })\in {\mathbb{R}}^2$ is the vector containing Coriolis force, centrifugal force, $K=diag(k_1,k_2)$ is joint stiffness coefficient matrix, $\tau =[\begin{array}{ll}{\tau }_1& {\tau }_2\end{array}{]}^T$ Output torque by joint motor.

Define positive definite and diagonal matrices $K_1=K\cdot {\epsilon }^2$, $\epsilon$ is a very small normal number. Order $z=K(\theta -q)$, then the system dynamics Eq. (4)- Eq. (5) can be written as follows:

3. Robust controller design based on neural network

The design idea of the proposed robust vibration suppression controller based on neural network is as follows.

Fig. 3Design idea of robust controller based on neural network

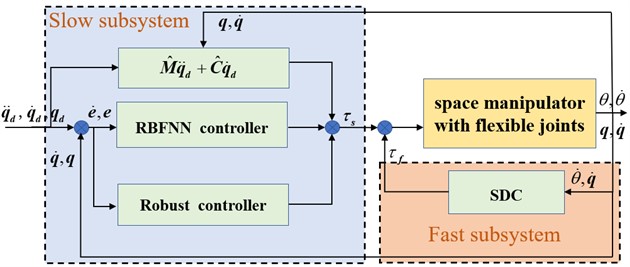
Based on singular perturbation theory, the dynamic model is split according to rigid and flexible characteristics. ${\tau }_s$ is the slow subsystem controller representing the rigid model, and ${\tau }_f$ is the fast subsystem controller representing the flexible model, so the total controller is designed as:

In order to suppress the flexible vibration caused by the fast subsystem model, a speed differential controller (SDC) is designed as:

where $K_f=K_2/\epsilon$, $K_2$ is a positive definite diagonal matrix.

Plug Eq. (9) into Eq. (7), then the dynamic equation of the fast subsystem:

If the joint is rigid, then $\theta =q$. The equivalent rigid model is the dynamic equation of the slowly subsystem:

where $N_s(q,\dot{q})$ replaces $N(q,\dot{q},\dot{\theta })$, when $\dot{\theta }=\dot{q}$.

Eq. (11) is rewritten as:

where $M\left(q\right)=D\left(q\right)+J_{\theta }$,$C(q,\dot{q})\in {\mathbb{R}}^2$.

Its form is not unique, but it can be satisfied by appropriate selection $x^T\left[\dot{M}\right(q)\ddot{q}-2C(q,\dot{q}\left)\right]x=0$, $\forall x\in {\mathbb{R}}^2$.

Considering that in practical engineering, it is impossible to obtain an accurate mathematical model $M$ and $C$, only its estimation model $\widehat{M}$ and $\widehat{C}$ can be obtained.

The controller is designed as follows:

where ${\tau }_c$ acts as compensate items, $q_d$ is the expected value.

Substituting Eq. (13) into Eq. (12), the following formula can be derived:

where $f(q,\dot{q})=\tilde{M}\left(q\right)({\ddot{q}}_d-\alpha \dot{e})+\tilde{C}(q,\dot{q})({\dot{q}}_d-\alpha e)+d$, $e=q-q_d$, $\tilde{M}=M-\widehat{M}$, $\tilde{C}=C-\widehat{C}$.

Let $x=(x_1,x_2{)}^T$, define:

From the above formula, Eq. (14) should be rewritten as:

Because radial basis function neural network (RBFNN) belongs to local generalization network and has fast operation speed, it is used to approximate the unknown model $f(q,\dot{q})$.

According to the nonlinear approximation ability of RBFNN, the following assumptions can be made [29-33]:

Assumption: Given an arbitrary small positive constant ${\epsilon }_M$, there exists an optimal weight vector $w^{\mathrm{*}}$, so that the approximation error$\epsilon$of neural network satisfies $\left|\epsilon \right|=\left|w^{\mathrm{*}T}\phi \right(x)-f(x\left)\right|<{\epsilon }_M$.

Then:

where $x=(q,\dot{q})$, ${\tau }_{NN}^{\mathrm{*}}$ is Neural network optimal control output.

The neural network controller is designed as:

where ${\tau }_{NN}^{}$ is the actual output of neural network, $\widehat{w}$ is the weight vector estimated value $w$,$\varphi (q,\dot{q})$ is Gaussian function.

That is:

where $c_j$ and ${\sigma }_j$ are the center value and the spread value of $j$th basis function respectively. $\left|\right|x-c_j\left|\right|$ is a norm of $x-c_j$.

$\epsilon$ can be used as external disturbance of the system. The form of affine nonlinear system with model error and external disturbance that Eq. (16) can be repaired and corrected is:

where, $f\left(x\right)=\left[\begin{array}{c}{x}_2-\alpha x_1\\ -M^{-1}(C{x}_2-u-{\tau }_c+{\tau }_{NN})\end{array}\right]g\left(x\right)=\left[\begin{array}{c}0\\ -M^{-1}\end{array}\right]$, $z=pe=p{x}_1$, $\alpha$ and $p$ are positive constants.

In order to show the ability of the control system to suppress interference, the following formula is defined as its performance index:

where $J$ is the gain $L_2$ of system Eq. (21).

The controller is designed to suppress elastic vibration and ensure the stability of the control system. That is, the controller can achieve a gain $J$ lower than the given value $k$.

The robust controller based on neural network is designed as:

The adaptive adjustment law of the weight parameters of the neural network is designed as:

where the gain $\eta >0$, the parameters $p$ meets [34]:

where ${\epsilon }_1$ represents given constant. Then the gain $J$ of $L_2$ of the closed-loop system is less than the given value $\gamma$.

Theorem: For the dynamic model Eq. (21), the total controller Eq. (13), neural network controller Eq. (19) and robust controller Eq. (23) are used. If there is a Lyapunov function $L\left(x\right)$ that satisfies the following HJI (Hamilton Jacobi Issacs) inequality, given $k>0$, if $L\left(x\right)\ge 0$ satisfy the following HJI inequality:

Then the gain $J$ of $L_2$ is less than a given value $k$.

Proof: Defining the following function Lyapunov:

where $\tilde{w}=w^{\mathrm{*}}-\widehat{w}$ represents estimation errors of the network weight. Then:

where putting Eq. (9) in the above Eq. (28), the paper can reach the following new expression:

Because:

Then:

That is, the gain of the closed-loop system $J$ of $L_2$ is less than a given value $k$.

4. Simulation experiment

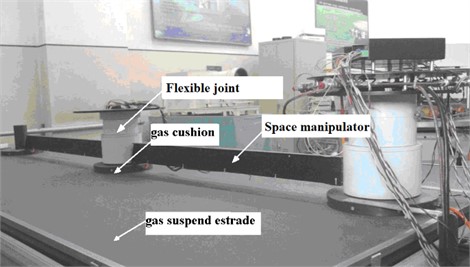
The free-floating two-links space robot as shown in Fig. 4 (Harbin Institute of Technology, Aerospace College, Aircraft Design Laboratory, 2022.5). which is used as a model to verify the effectiveness of the proposed control scheme.

Fig. 42-DOF space manipulator in micro-gravity (Harbin Institute of Technology, 2022.5)

Taking the flexible double joint space robot manipulator as an example, In this simulation, the following reality robot manipulators parameters are chosen [15]: manipulator arm 1 is 2 m, manipulator arm 2 is 1.5 m, $m_1=m_2=$ 2.5 kg, $J_1=$2 kg⋅m², $J_2=$1 kg⋅m², $m_1=$ 1.5 kg, $m_2=$7.5 kg, $r_1=$1.2 m, $r_2=$1.8 m, $J_1=J_2=$6.5 kg⋅m².

External disturbance:$[q_{1}0.1\mathrm{s}\mathrm{i}\mathrm{n}t,q_{2}0.1\mathrm{s}\mathrm{i}\mathrm{n}t{]}^T$.

Desired trajectory: $q_{1d}=2+0.1\mathrm{s}\mathrm{i}\mathrm{n}t$; $q_{2d}=2-0.1\mathrm{s}\mathrm{i}\mathrm{n}t$.

Estimated values: ${\widehat{m}}_1=$ 1.2 kg, ${\widehat{m}}_2=$ 6.5 kg.

The simulation parameters: $\alpha =$30, $\gamma =$ 100, $k=$ 0.1.

The initial joint position and velocity are chosen as 0, network initial weights are 0, the width of Gaussian function is 10, the centers of the Gaussian function are randomly selected between 0 and 1.

In order to verify the superiority of the proposed algorithm, the algorithm in this paper is compared with the classical PID control algorithm. For the convenience of expression, the neural network control algorithm based on H_∞ proposed in this paper is referred to as “NNC”, and the classical PID algorithm is referred to as “PID”. The simulation results are shown in Fig. 5-Fig. 10. Fig. 5-Fig. 7 shows the effect of opening the controller ${\tau }_f$ and using fast and slow composite controller. Fig. 8-Fig. 10 shows the effect of switching off the controller ${\tau }_f$ and using only the fast controller.

4.1. Switching on the controller ${\mathit{\tau }}_{\mathit{f}}$

It can be seen from Fig. 5(a) that the PID controller can achieve good tracking effect in about 8 s. It can be seen from Fig. 5(b) that the NNC algorithm in this paper can ensure that the actual trajectory can quickly track the desired trajectory curve in about 3 s. When the initial error of joint 1 is large, its actual trajectory can accurately track the desired trajectory in less than 3 s; The actual trajectory of joint 2 can accurately track the desired trajectory in about 2 s. It can be seen from Fig. 6 that the maximum error between the angle of joint 1 and the angle of the electronic rotor is about 0.3 rad, and the minimum error between the angle of joint 2 and the angle of the electronic rotor is about 0.1 rad, but both error angles converge to 0 within 2 s; The control of elastic vibration is realized.

Fig. 5Tracking curves of joints: tracking curves based on PID controller (above) and tracking curves of the proposed NNC algorithm (below)

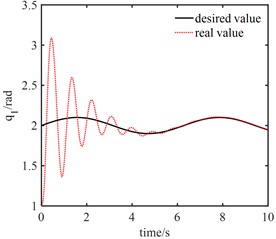
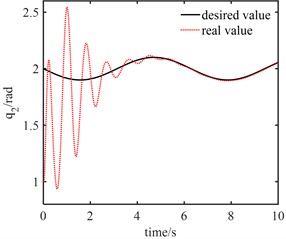
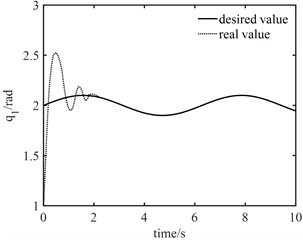
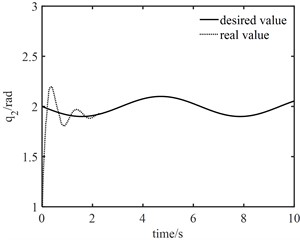
Fig. 6Angle errors between joint angle q and rotor angle θ

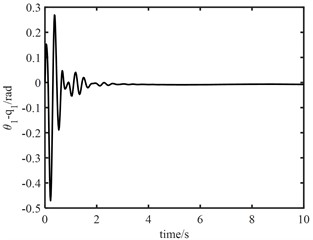
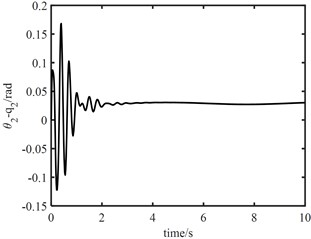
It can be seen from Fig. 7 that the torque output of the model error controller tends to zero approximately 2 s later. It can be seen from Fig. 8 that the joint torque oscillates at the initial stage, but it is not large. The maximum output torque of joint 1 control torque is 10 N.m, and the minimum output torque of joint 2 control torque is 7 N.m. This shows that the proposed algorithm is effective. The robust controller based on neural network can effectively track the desired trajectory, and the fast subsystem controller can suppress the vibration of flexible joints.

Fig. 7Control output signal u

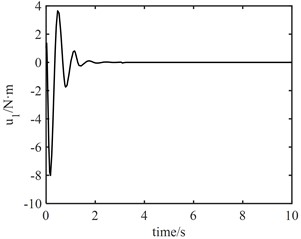
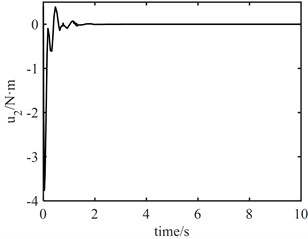
Fig. 8Control output signal τ

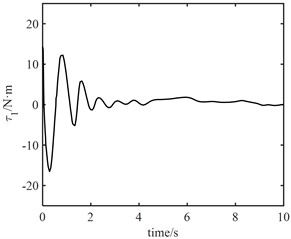
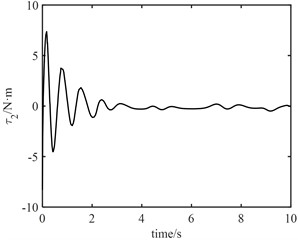
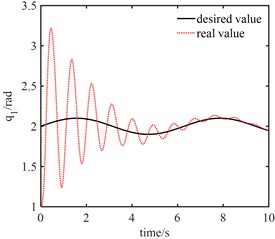
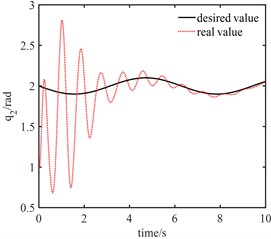
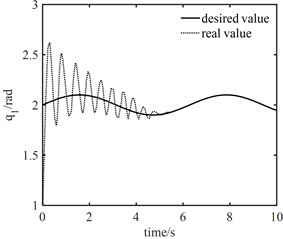
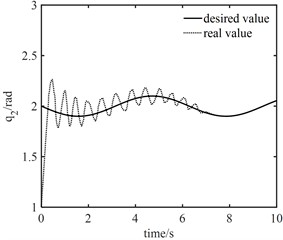
Fig. 9Tracking curves of joints: tracking curves based on PID controller (above) and tracking curves of the proposed NNC algorithm (below)

4.2. Switching off the controller ${\mathit{\tau }}_{\mathit{f}}$

From Fig. 9(a), PID controller can achieve good tracking effect in about 10 s. It can be seen from Fig. 9(b) that when the fast-change subsystem controller ${\tau }_f$ is turned off, only the slow subsystem controller can still ensure that the actual trajectory can track the desired trajectory after a long period of vibration, in which joint 1 accurately tracks the desired trajectory in about 5 s and joint 2 accurately tracks the desired trajectory in about 7 s. This shows that the designed robust controller based on neural network not only realizes the gradual reduction of tracking error, but also has strong robustness to elastic vibration.

Fig. 10Angle errors between joint angle q and rotor angle θ

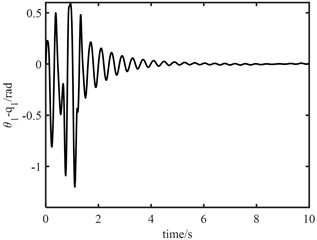
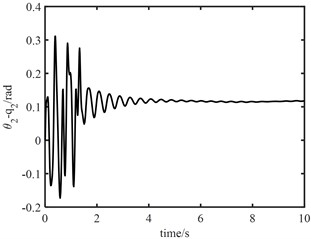
Fig. 11Control output signal u

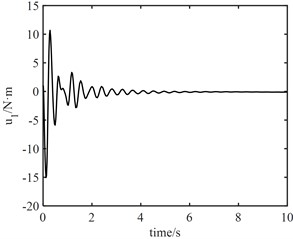
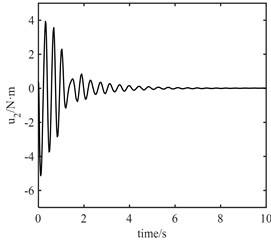
Fig. 12Control output signal τ

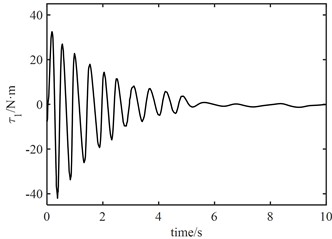
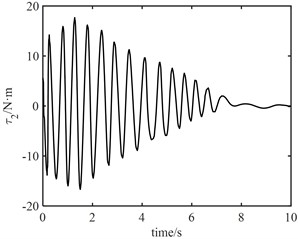
It can be seen from Fig. 10 that the maximum error between joint 1 angle and electronic rotor angle is about 1.0 rad, and the maximum error between joint 2 angle and electronic rotor angle is about 0.3 rad, but both error angles converge to 0 within 2 s, the control of elastic vibration is realized. It can be seen from Fig. 11 that the torque output of the model error controller tends to zero approximately 6 s later. From Fig. 12, it can be seen that the control torque not only increases significantly, but also the maximum torque of joint 1 is about 30 N.m. The torque of joint 2 is about 20 N.m. Moreover, the vibration time of the joint torque is obviously longer, and it tends to be stable at about 7 s. It also shows that the designed controller ${\tau }_f$ of the fast subsystem is effective, which can effectively suppress the vibration, reduce the vibration time and improve the control accuracy.

5. Conclusions

Aiming at the uncertainty of modeling inaccuracy, external interference and joint flexibility in engineering practice, a neural network robust control method based on H_∞ is proposed. The dynamic model of a free-floating space robot with flexible joints is established, and a RBF neural network compensation controller based on H_∞ theory is designed to approximate the uncertain model terms. The approximation error is eliminated by a robust controller. The adaptive online learning rate of neural network weights is designed. A feedback compensation controller based on velocity difference is designed to suppress the elastic vibration for the fast subsystem model. Based on Lyapunov theory, it is proved that the designed controller can ensure that the L₂ gain of the system is less than the given index. Finally, the simulation results verify the effectiveness of the proposed method, which has a good reference value for engineering.