Simulation of dynamic performance and wheel-rail wear of railway wagon under deviation of cargo gravity center

Song, Wei; Wang, Junguo; Zhao, Yongxiang

doi:10.21595/vp.2022.22908

Vibroengineering Procedia

Browse Procedia

Published: 22 October 2022

Check for updates

Simulation of dynamic performance and wheel-rail wear of railway wagon under deviation of cargo gravity center

Wei Song¹

Junguo Wang²

Yongxiang Zhao³

^{1, 2, 3}School of Mechanical Engineering, Southwest Jiaotong University, Chengdu, China

Corresponding Author:

Junguo Wang

Cite the article Download PDF

Downloads 345

CrossRef Citations 3

Abstract

A multibody dynamic model of railway wagon is established by Simpack software, and the derailment coefficient, wheel load reduction rate, impact angle and wear index of freight car are calculated under different gravity center offsets and different curve conditions. The simulation results show that the lateral and longitudinal offsets of cargo gravity center have a great influence on the derailment coefficient, wheel unloading rate, impact angle and wear index of the vehicle. The larger the offset of the cargo gravity center is, the worse the operation performance of the wagon is, the more serious the wheel-rail wear is, and the shorter the transport life of the wagon is. The smaller the radius of the curve is, the greater the impact is.

Simulation of dynamic performance and wheel-rail wear of railway wagon under deviation of cargo gravity center

Highlights

The simplified static model and the multibody dynamic model of a railway freight car is established under different gravity center offsets and different curve conditions.
The derailment coefficient, wheel load reduction rate and impact angle are calculated, the results show that the center of gravity offset has a greater impact on the performance of the wagon. The greater the offset, the worse the performance.
The wear index is calculated, the result shows that the center of gravity offset has a greater impact on the wheel-rail wear of the wagon. The greater the offset, the more serious the wheel-rail wear, the shorter the transport life of the wagon.
With the decrease of curve radius, the deviation of cargo center of gravity has a greater impact on the operation performance and wheel-rail wear.

1. Introduction

With the rapid development of railway transportation, the operating environment has changed greatly, which puts forward higher requirements for vehicle operation efficiency and safety [1]. When the center of gravity of goods deviates, wheel-rail contact is affected, resulting in derailment of freight cars, thus affecting transport efficiency and safety. In reference [2], a numerical model between the longitudinal offset of the cargo center of gravity and derailment coefficient was established. In reference [3], the maximum transverse and longitudinal offsets of the cargo center of gravity after reducing the vehicle load were obtained. In Reference [4], the lateral allowable offset of freight car center of gravity under different loading conditions was analyzed. In Reference [5], the influence of natural vibration characteristics on wheel wear was studied. In Reference [6], the multi-angle wear evolution of the wheel was studied, and the general conditions for the polygonal wear evolution were established. In reference [7], the wheel wear of heavy-duty rail wagon with different axle loads was studied based on Archard wear model.

Previous studies mainly analyzed the influence of cargo center of gravity deviation on vehicle operation safety, but there are few studies on the influence of cargo center of gravity deviation on wheel-rail wear. This paper presents a heavy truck model, the influence of cargo center of gravity deviation on the operation performance and wheel-rail wear is analyzed by calculating the wheel derailment coefficient, wheel unloading rate, impact angle and wear index under curve conditions.

2. Modelling

2.1. Simplified model of railway wagon

When the goods move horizontally or vertically, the position of the center of gravity of the goods on the car body changes, and the stress of the bogie will also change, which affects the vehicle operation performance and wheel-rail wear.

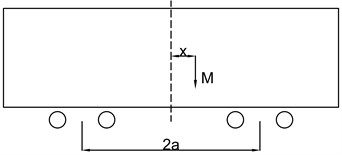
When the center of gravity of goods shifts laterally, there exists following equations:

1

P_{1} = \frac{1}{8} M g (1 + \frac{y}{b}) - \frac{1}{8} \sum F \cdot \frac{h}{b},

2

P_{2} = \frac{1}{8} M g (1 - \frac{y}{b}) + \frac{1}{8} \sum F \cdot \frac{h}{b},

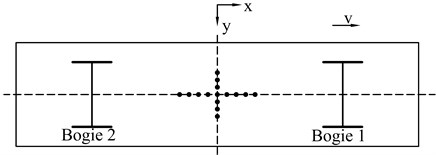
where $P_{1}$ and $P_{2}$ are the wheel-rail vertical force, $b$ is half lateral span, $y$ is lateral offset of the center of gravity, $h$ is center of gravity height, $m$ is weight of the wheelset, $\sum F$ is the lateral force. When the center of gravity of goods shifts longitudinally, there exists following equations:

3

P_{f} = \frac{M g}{4} (1 + \frac{x}{a}),

4

P_{r} = \frac{M g}{4} (1 - \frac{x}{a}),

where $P_{f}$ and $P_{r}$ are the wheelset axle weights of the front and rear bogies, a is half vehicle spacing, $x$ is longitudinal offset of the center of gravity. If $F_{c}$ is wagon centrifugal force, $α$ is the curve superelevation angle, lateral force is expressed as:

5

\sum F = F_{c} c o s α - M g s i n α .

Fig. 1Forces analysis of wagon: a) distribution of cargo gravity center, b) longitudinal offset of gravity center, c) lateral offset of gravity center, d) stress analysis passing curve

Forces analysis of wagon: a) distribution of cargo gravity center, b) longitudinal offset of gravity center, c) lateral offset of gravity center, d) stress analysis passing curve

a)

b)

c)

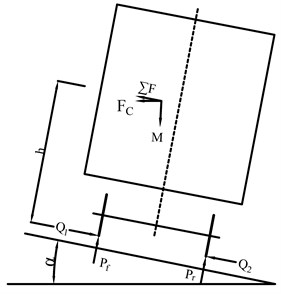
d)

2.2. Vehicle system dynamics model

The SIMPACK software is used to establish the C80 wagon dynamics model, which consists of train body and E22 bogie. The bogie is mainly composed of bolster, side frame, wheelset, axle box device, foundation brake device, cross support device, elastic side bearing, elastic suspension device and damping device. The topology of vehicle dynamics model is shown in Fig. 2.

The system model has 68 DOF as shown in Table 1, and FASTSIM method is used to calculate the creep force, where the wheel-rail friction coefficient is 0.35 and the Kalker coefficient is 1.0.

Fig. 2Topology of multibody dynamics model

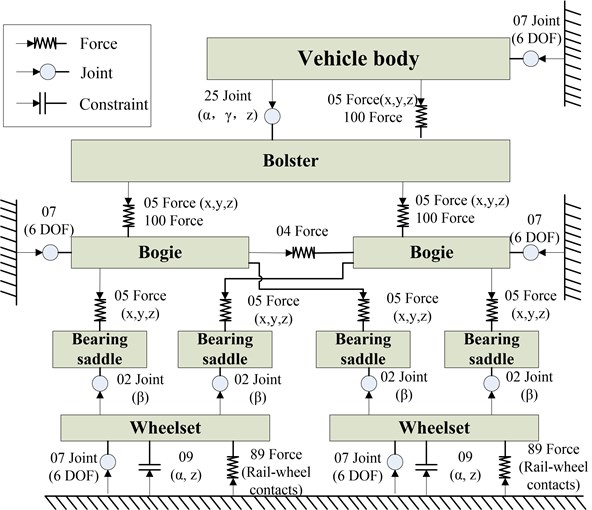
Table 1Degree of freedom of vehicle dynamics model

Component	Longitudinal displacement	Lateral displacement	Vertical displacement	Roll	Pitch	Yaw
Vehicle body	$X_{c}$	$Y_{c}$	$Z_{c}$	$ϕ_{c}$	$θ_{c}$	$ψ_{c}$
Bolster ( $i =$ 2)	–	–	$Z_{b}$	$ϕ_{b}$	–	$ψ_{b}$
Bogie ( $i =$ 4)	$X_{s b}$	$Y_{s b}$	$Z_{s b}$	$ϕ_{s b}$	$θ_{s b}$	$ψ_{s b}$
Bearing saddle ( $i =$ 8)	–	–	–	–	$θ_{g}$	–
Wheelset ( $i =$ 4)	$X_{w}$	$Y_{w}$	$Z_{w}$	$ϕ_{w}$	$θ_{w}$	$ψ_{w}$

3. Dynamics performance index

3.1. Derailment coefficient

The ratio of the lateral force $Q$ of wheel-rail to the vertical force $P$ of wheel-rail at the moment of wheel running is called as derailment coefficient, and its calculation formula is as follows:

6

\{\begin{array}{l} \begin{array}{l} \frac{Q}{P} \leq 1.2, & (250 m \leq R \leq 400 m), \end{array} \\ \begin{array}{l} \frac{Q}{P} \leq 1.0, & (R > 400 m) . \end{array} \end{array}

3.2. Wheel unloading rate

It is defined as ratio of wheel load reduction $Δ P$ to average wheel weight $\bar{P}$ of axle as follows:

7

\{\begin{array}{l} \begin{array}{l} \frac{Δ P}{\bar{P}} \leq 0.65, & (v \leq 160 k m / h), \end{array} \\ \begin{array}{l} \frac{Δ P}{\bar{P}} \leq 0.8, & (v > 160 k m / h) . \end{array} \end{array}

3.3. Wear index

If $W_{D}$ is the wear index, $T_{x}$ and $T_{y}$ are longitudinal and transverse creep force, $γ_{x}$ and $γ_{y}$ are longitudinal and transverse creep rate, $M_{z}$ is spin creep torque, $φ_{z}$ is spin creep coefficient, the wear index is then calculated as follow:

8

W_{D} = T_{x} γ_{x} + T_{y} γ_{y} + M_{Z} φ_{z} .

4. Simulation results and analysis

4.1. Simulation of line conditions

The American track spectrum is adopted to simulate the actual curve route conditions, the maximum allowable lateral offset and longitudinal offset are 0.1 m and 0.5 m respectively. The center of gravity changes between –0.25 m and 0.25 m in the transverse direction and between –3 m and 3 m in the longitudinal direction. Table 2 shows some simulation conditions.

Table 2Simulation of line conditions

Item	Radius (m)	Ultra-high (mm)	Velocity (km/h)
1	400	110	60
2	500	100	60
3	600	80	60

4.2. Lateral offset of center of gravity

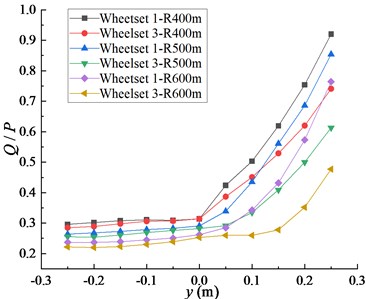
Fig. 3(a) shows the effect of lateral offset of cargo center of gravity on wheel derailment coefficient. When the center of gravity changes from 0 to –0.25 m, the derailment coefficient of the wheelset 1 and wheelset 3 decreases slowly and uniformly, and the derailment coefficient of the wheelset 1 is larger than that of the wheelset 3. When the center of gravity changes from 0 m to 0.25 m horizontally, the derailment coefficients of the wheelset 1 and wheelset 3 increase rapidly. Among them, the increase of the wheelset 1 is greater than that of the wheelset 3.

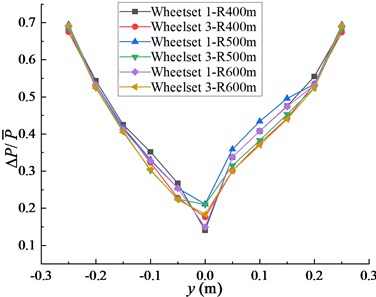
Fig. 3(b) shows the effect of lateral offset of cargo center of gravity on wheel unloading rate. When the gravity center moves horizontally from 0 to −0.25 m and 0.25 m, the wheel unloading rates of the wheelset 1 and wheelset 3 increase rapidly, and the wheel unloading rate of the wheelset 1 is gradually greater than that of the wheelset 3. When the lateral offsets are −0.25 m and 0.25 m, the wheel unloading rate has exceeded the limit of 0.65 specified in the standard. When the lateral offset is 0 m, the wheel unloading rate is the minimum.

Fig. 3a) Influence of lateral offset of cargo gravity center on derailment coefficient, b) influence of lateral offset of cargo gravity center on wheel unloading rate

a) Influence of lateral offset of cargo gravity center on derailment coefficient, b) influence of lateral offset of cargo gravity center on wheel unloading rate

a)

b)

Fig. 4(a) shows the effect of lateral offset of cargo center of gravity on wheel attack angle. When the center of gravity changes from 0 m to –0.25 m, the attack angle of the wheelset 1 increases rapidly, and from 0.5 m to 0.25, the attack angle of the wheelset 1 increases slowly. The lateral offset of center of gravity has little effect on the attack angle of the wheelset 3.

Fig. 4(b) shows the effect of lateral offset of cargo center of gravity on wheel-rail wear index. When the center of gravity moves along 0 m to –0.25 m and 0.25 m, the wear degree of wheelset 1 increases rapidly, and the wear degree of wheelset 3 increases slowly. Under the same lateral offset of gravity center, the wear degree of wheelset gradually decreases with the increase of the radius of the freight car passing through the curve.

Fig. 4a) Influence of lateral offset of cargo gravity center on wheel attack angle, b) influence of lateral offset of cargo gravity center on wheel-rail wear index

a) Influence of lateral offset of cargo gravity center on wheel attack angle, b) influence of lateral offset of cargo gravity center on wheel-rail wear index

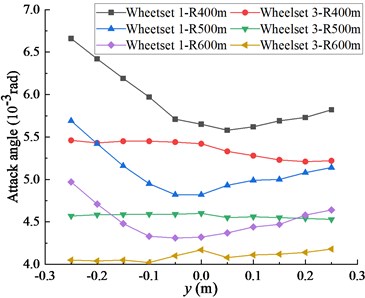
a)

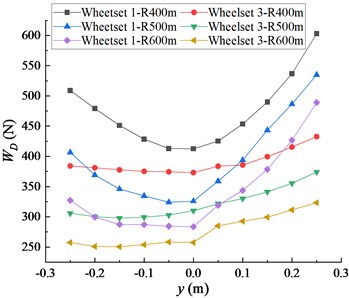
b)

4.3. Longitudinal offset of center of gravity

Fig. 5(a) shows the effect of longitudinal offset of cargo gravity center on derailment coefficient. When the center of gravity changes from –3 m to 3 m along the longitudinal direction, the derailment coefficient of wheelset 1 decreases and that of wheelset 3 increases. When the center of gravity moves from 0 m to –3 m longitudinally, the derailment coefficient of wheelset 1 is greater than that of wheelset 3. When the center of gravity moves from 0 m to 3 m longitudinally, the derailment coefficient of wheelset 3 is greater than that of wheelset 1.

Fig. 5(b) shows the effect of vertical offset of cargo center of gravity on wheel unloading rate. When the center of gravity changes from 0 to –3 m, the wheel unloading rate of wheelset 1 increases rapidly, and the wheel unloading rate of wheelset 3 decreases slowly. When the center of gravity changes from 0 m to 3 m, the wheel unloading rate of wheelset 3 increases gradually, while the wheel unloading rate of wheelset 1 decreases slowly.

Fig. 6(a) shows the effect of longitudinal offset of cargo center of gravity on wheel attack angle. When the offset of center of gravity is 0.5 m, the attack angles of wheelset 1 and 3 are the same. When the center of gravity moves from 0.5 m to −3 m along the longitudinal direction, the attack angle of wheelset 1 increases and has always been greater than that of wheelset 3, so the performance of wagon passing curve decreases. When the center of gravity moves from 0.5 m to 3 m along the longitudinal direction, the attack angle of wheelset 3 increases, and the attack angle of wheelset 3 is always greater than that of wheelset 1, so the performance of wagon passing curve decreases. When the center of gravity deviates, the radius of the curve increases, and the attack angle decreases accordingly, so as to improve the passing curve performance of freight cars.

Fig. 6(b) shows the effect of longitudinal offset of cargo center of gravity on wheel-rail wear. When the center of gravity moves from 0 m to 3 m longitudinally, the wheel-rail wear of wheelset 1 increases. When the center of gravity moves from 0 m to –3 m longitudinally, the wheel-rail wear of wheelset 3 increases. Under the same lateral offset of gravity center, the wear degree of wheelset gradually decreases with the increase of the radius of the freight car passing through the curve.

Fig. 5a) Influence of longitudinal offset of cargo gravity center on derailment coefficient, b) influence of longitudinal offset of cargo gravity center on wheel unloading rate

a) Influence of longitudinal offset of cargo gravity center on derailment coefficient, b) influence of longitudinal offset of cargo gravity center on wheel unloading rate

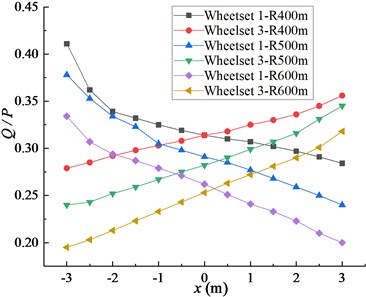
a)

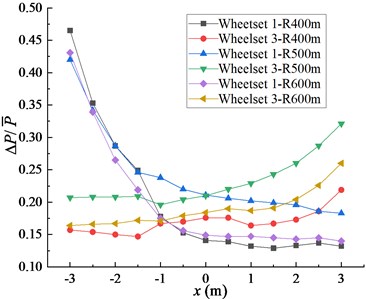
b)

Fig. 6a) Influence of longitudinal offset of cargo gravity center on wheel attack angle, b) influence of longitudinal offset of cargo gravity center on wheel-rail wear index

a) Influence of longitudinal offset of cargo gravity center on wheel attack angle, b) influence of longitudinal offset of cargo gravity center on wheel-rail wear index

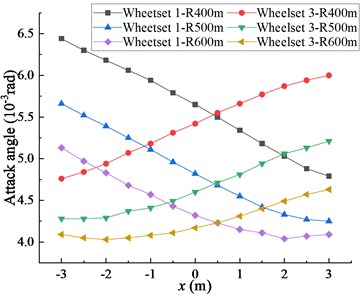
a)

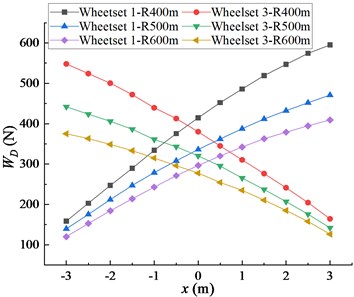
b)

5. Conclusions

1) When the center of gravity is shifted laterally, the wheel unloading rate increases, and the change trend is the same under different curve conditions. The attack angle of wheelset 1 and the wheel-rail wear index of wheelset 1 and 3 increase, the worse the vehicle curve operation performance is, and the wheel-rail wear is serious. When the center of gravity is shifted right, the derailment coefficient of the guide wheel increases greatly.

2) When the center of gravity of the goods deviates longitudinally, the operation performance of the freight car curve decreases. When the center of gravity moves forward, the wheel-rail wear of wheelset 1 increases. When the center of gravity moves backward, the wheel-rail wear of wheelset 3 increases.

3) The larger the deviation of the cargo center of gravity is, the worse the operation performance of the freight car is, and the more serious the wheel-rail wear is, which leads to the decrease of the safety of the freight car and the decrease of the transportation life. Therefore, the center of gravity of goods should be avoided as far as possible. If the center of gravity of goods deviates, increasing the curve radius can improve the operation performance of freight cars and reduce wheel-rail wear.

References

W. Wang, Q. Y. Peng, Q. Wang, and X. B. Xiao, “Effect analysis of coupler force on heavy-haul train safety under eccentric loads,” Journal of Southwest Jiaotong University, Vol. 56, pp. 378–384, 2021.

Search CrossRef
C. Chen, M. Han, and Y. L. Wang, “Study on allowable lateral deviation of the center of gravity of goods based on safety criteria regarding derailment coefficient,” Journal of the China Railway Society, Vol. 30, pp. 12–16, 2008.

Search CrossRef
L. Y. Zhang and X. Zhang, “Study on freight longitudinal allowable deflection based on safety criteria for derail coefficient,” Railway Transport and Economy, Vol. 33, pp. 81–85, 2011.

Search CrossRef
J. J. Sun and Z. S. Ren, “Research on the safety range of COG (Center of Gravity) deviation of goods on XL25G luggage cars,” Rolling Stock, Vol. 47, pp. 1–5, 2009.

Search CrossRef
G. Tao, Z. Wen, Q. Guan, X. Zhao, Y. Luo, and X. Jin, “Locomotive wheel wear simulation in complex environment of wheel-rail interface,” Wear, Vol. 430-431, pp. 214–221, Jul. 2019, https://doi.org/10.1016/j.wear.2019.05.012

Publisher
B. Peng, S. Iwnicki, P. Shackleton, and Y. Song, “General conditions for railway wheel polygonal wear to evolve,” Vehicle System Dynamics, Vol. 59, No. 4, pp. 568–587, Apr. 2021, https://doi.org/10.1080/00423114.2019.1697458

Publisher
P. P. Shao, M. H. Fu, Y. Zhou, and L. L. Yang, “Research on the evaluation of wheel-rail wear of heavy haul railway based on Archard’s model,” Railway Locomotive and Car, Vol. 32, pp. 42–45, 2012.

Search CrossRef

Cited by

Using numerical simulation to analyze the strength properties of the developed demountable body of a trolley

R A Peshkov | P A Tretyakov | A V Fedorov | D V Kuplevatsky | A V Mineev

(2024)

Effect of line parameters on wheel wear of heavy–haul freight vehicle

Hongkun Wang | Yongxiang Zhao | Yayun Qi | Yufeng Cao

(2024)

Study on the Mechanism of Wheel Asymmetric Wear of Heavy-Haul Freight Vehicles

(2024)

About this article

Received

21 August 2022

Accepted

09 September 2022

Published

22 October 2022

SUBJECTS

Vibration in transportation engineering

DOI

https://doi.org/10.21595/vp.2022.22908

Keywords

railway wagon

multibody dynamics

derailment

wear

Acknowledgements

The work is supported by Sichuan Science and Technology Program (No. 2020YFH0080) and Sci. & tech. innovation project of Shenhua Railway Freight Car Trans. Co., Ltd (SHGF-13-77).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2024 02 23

Influence of sliding wear on contact characteristics based on 3-D wheel/rail contact model

Jihao Han, Yunpeng Wei, Tao Yang

Research article

2024 01 21

Effect of train traction on the wheel polygonal wear of high-speed trains

Tiancheng Tang, Zengchuang Zhao, Bowen Wu, Wenjing Wang, Jiabao Pan

Research article

2023 09 21

Multibody system dynamics modelling and simulation of a high-speed train for its suspension optimization

Yongming Wu, Shiping Liu, Dazhuo Wu, Wenlin Wang

Research article

2023 09 21

Effect of an inter-vehicle damper on the dynamics of a high-speed train

Wenlin Wang, Shiping Liu, Dazhuo Wu

W. Song, J. Wang, and Y. Zhao, “Simulation of dynamic performance and wheel-rail wear of railway wagon under deviation of cargo gravity center,” Vibroengineering PROCEDIA, Vol. 45, pp. 46–52, Oct. 2022, https://doi.org/10.21595/vp.2022.22908

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2022.22908
UR  - https://doi.org/10.21595/vp.2022.22908
TI  - Simulation of dynamic performance and wheel-rail wear of railway wagon under deviation of cargo gravity center
T2  - Vibroengineering PROCEDIA
AU  - Song, Wei
AU  - Wang, Junguo
AU  - Zhao, Yongxiang
PY  - 2022
DA  - 2022/10/22
PB  - JVE International Ltd.
SP  - 46-52
VL  - 45
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Song_2022,
	doi = {10.21595/vp.2022.22908},
	url = {https://doi.org/10.21595/vp.2022.22908},
	year = 2022,
	month = {oct},
	publisher = {{JVE} International Ltd.},
	volume = {45},
	pages = {46--52},
	author = {Wei Song and Junguo Wang and Yongxiang Zhao},
	title = {Simulation of dynamic performance and wheel-rail wear of railway wagon under deviation of cargo gravity center},
	journal = {59th International Conference on Vibroengineering in Dubai, United Arab Emirates, October 22, 2022}
}

Copy Bibtex

Copied to clipboard!

[1]W. Song, J. Wang, and Y. Zhao, “Simulation of dynamic performance and wheel-rail wear of railway wagon under deviation of cargo gravity center,” Vibroengineering PROCEDIA, vol. 45, pp. 46–52, Oct. 2022, doi: 10.21595/vp.2022.22908.

Copy IEEE

Copied to clipboard!

Song, Wei, Junguo Wang, and Yongxiang Zhao. “Simulation of Dynamic Performance and Wheel-Rail Wear of Railway Wagon under Deviation of Cargo Gravity Center.” Vibroengineering PROCEDIA 45 (October 22, 2022): 46–52. https://doi.org/10.21595/vp.2022.22908.

Copy Chicago

Copied to clipboard!

Simulation of dynamic performance and wheel-rail wear of railway wagon under deviation of cargo gravity center

Abstract

Highlights

1. Introduction

2. Modelling

2.1. Simplified model of railway wagon

2.2. Vehicle system dynamics model

3. Dynamics performance index

3.1. Derailment coefficient

3.2. Wheel unloading rate

3.3. Wear index

4. Simulation results and analysis

4.1. Simulation of line conditions

4.2. Lateral offset of center of gravity

4.3. Longitudinal offset of center of gravity

5. Conclusions

References

Cited by

About this article

Related Articles