Multibody system dynamics modelling and simulation of a high-speed train for its suspension optimization

2.1. Modelling the nonlinear components

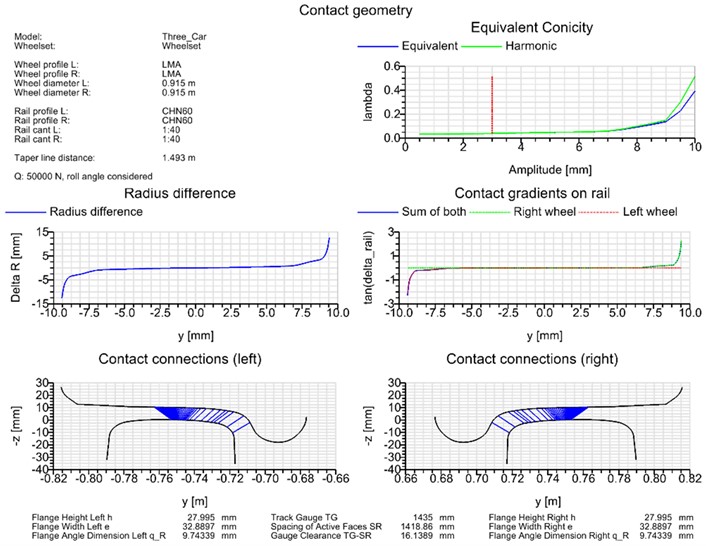
MBS modelling of the above CRH train is carried out in the SIMPACK software environment. In modelling nonlinear wheel-rail contact, the Chinese LMA worn wheel profile and the CN 60 kg/m Chinese standard rail profile are used, the simplified Kalker’s law is employed to calculate the creep force, thus, the obtained nonlinear geometry of wheel-rail contact is demonstrated by Fig. 2.

Fig. 2The nonlinear geometry of wheel-rail contact

The suspension system includes the primary suspension with coil spring and axle damper, the secondary suspension with air springs and vertical and lateral hydraulic dampers and the inter-car suspension with coupler and draft gear, and with inter-car hydraulic dampers.

In modelling the nonlinear railroad irregularities, the American fifth grade track profiles are used as track inputs, in which the vertical and alignment profile spectrums are respectively formulated by:

and:

the cross level and gauge profile spectrums are formulated by:

where the meaning, value and dimension of the parameter symbols in Eqs. (1-3) are documented in Table 2. Thus, the final nonlinear railroad irregularities in time domain are obtained and shown in Fig. 3.

Fig. 3The obtained nonlinear random a) vertical and b) lateral railroad irregularity profiles

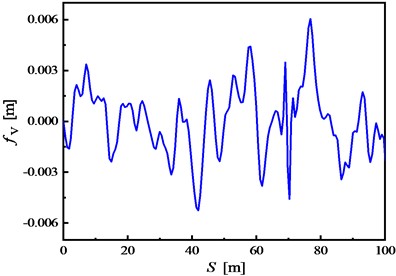
a)

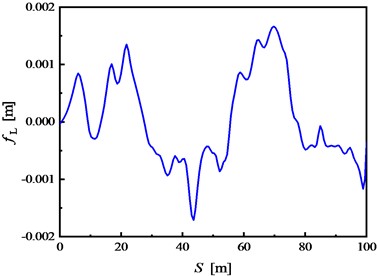
b)

2.2. The main dynamic indices

The ride comfort index $W$ for simulation of the high-speed train can be calculated by:

where $A$ is the car-body vibration acceleration (m/s²), $f$ is vibration frequency (Hz) and $F\left(f\right)$ is coefficient for frequency correction. Thus, the class for ride comfort evaluation of the high-speed train calculated by Eq. (4) can be shown by Table 2.

In addition, the derailment coefficient $N$ for evaluating curving behavior of the high-speed train can be calculated by:

where $Q$ is the wheel-rail lateral force (kN), $P$ is the wheel-rail vertical force (kN), $\alpha$ is the angle of wheel flange (rad) and $\mu$ is the wheel-rail friction coefficient.

2.3. MBS model of the high-speed train

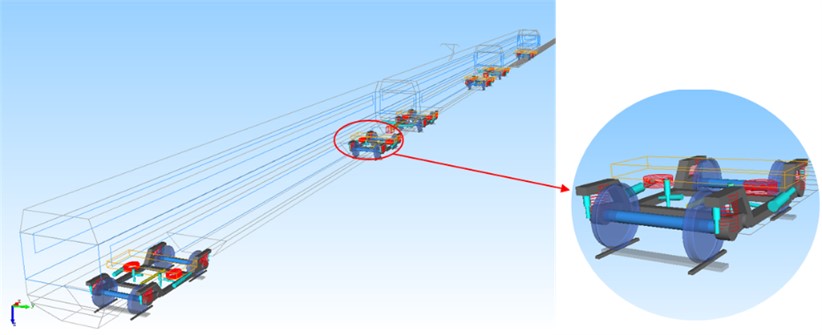
The finally obtained MBS model of the CRH train is illustrated in Fig. 4, for simplicity, this model consists of three vehicles “Mc-Tp-M”. Followed nominal force calculation shows that the acceleration of the MBS model in its equilibrium state is 6.24E-10 m/s², which is far less than the evaluation criteria of 1E-4 m/s², indicating that the established MBS model is pretty accurate.

Fig. 4MBS model of the CRH high-speed train

3.1. Nonlinear stability

Vehicle system dynamics of the CRH train are simulated by using the above MBS model. Fig. 5 demonstrates nonlinear stability characteristics of the train. As an example, Fig. 5(a) shows lateral excursion behavior of the No. 3 wheelset of the head carat different speeds, Fig. 5(a) illustrates that when vehicle speed equals to or exceeds 380 km/h, lateral vibration of the No. 3 wheelset diverges, thus, critical speed of the head car is 380 km/h.

Fig. 5(b) summarizes the wheelset lateral excursion limit cycles of the three vehicles. Fig. 5(b) indicates that when vehicle speed falls between 370-380 km/h, limit cycles of the three vehicles occur, thus, it can be concluded from the simulation that nonlinear critical speed of the CRH train is 378 km/h, which is consistent with the actual test result of the CRH train [12].

3.2. Ride comfort

Fig. 6 demonstrates riding performance of the CRH train. As an example, Fig. 6(a) shows lateral acceleration of the middle car-body at different speeds, it indicates that the accelerations fall within a scope of –0.5 m/s²~0.4 m/s², which means good ride comfort.

Fig. 5Nonlinear stability characteristics of the CRH train: a) lateral excursion of the No. 3 wheelset of the head car, b) wheelset lateral excursion limit cycles of the three vehicles

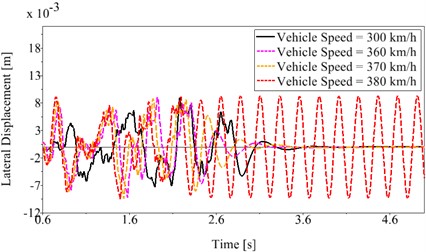
a)

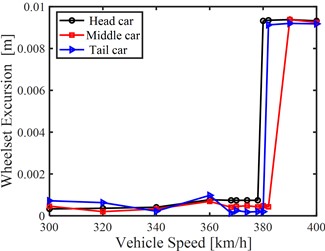
b)

Fig. 6(b) concretely summarizes the vertical and lateral ride comfort indices of the three vehicles, referring to Table 2, vertical ride comfort of the CRH train is in “Excellent” level, while lateral ride comfort of the CRH train is in “Good” level. The simulated ride comfort results also agree well with actual test result of the CRH train [12].

Fig. 6Riding performance of the CRH train: a) lateral acceleration of the middle car-body, b) vertical and lateral ride comfort indices of the three vehicles

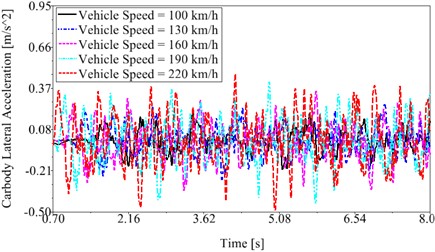
a)

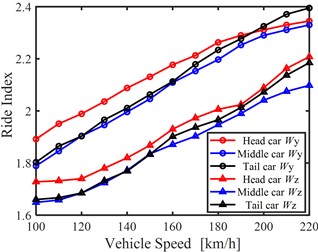
b)

3.3. Curve negotiation performance

Fig. 7 demonstrates curving behavior of the CRH train.

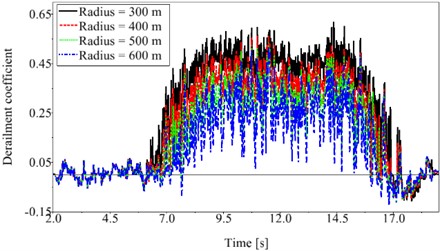
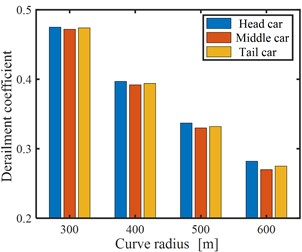
Fig. 7Curving behavior of the CRH train: a) derailment coefficient profile of the middle car, b) a summary of RMS derailment coefficients of the three vehicles

a)

b)

Fig. 7(a) shows derailment coefficient profiles of the middle car when it is passing through different curves at a constant speed of 80 km/h, Fig. 7(a) indicates that the maximum derailment coefficient is less than 0.6 when the train is negotiating a tight curve with 300 m radius.

In addition, Fig. 7(b) summarizes the RMS derailment coefficients of the three vehicles, Fig. 7(b) indicates that curving performance of CRH train is good. The simulated derailment coefficient level is also consistent with the actual test result and field curving performance of the CRH train [12].