Effect of vehicle-track vertical coupling vibrations on frame-mounted traction motor dynamics

Yu, Yuewei; Zhao, Leilei; Zhou, Changcheng

doi:10.21595/jve.2019.20900

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 February 2020

Check for updates

Effect of vehicle-track vertical coupling vibrations on frame-mounted traction motor dynamics

Yuewei Yu¹

Leilei Zhao²

Changcheng Zhou³

^{1, 2, 3}School of Transportation and Vehicle Engineering, Shandong University of Technology, Zibo, China

Corresponding Author:

Changcheng Zhou

Cite the article Download PDF

Downloads 1431

WoS Core Citations 1

CrossRef Citations 1

Abstract

In order to reveal the effect of the vehicle-track vertical coupling vibrations on the frame-mounted traction motor dynamics, a vehicle-track vertical coupling dynamic model with considering the influence of the frame-mounted traction motor is established, and the correctness of the model is verified by real vehicle test. In case of the investigated vehicle model, the influences of the vehicle-track vertical coupling vibrations and the suspension parameters on the frame-mounted traction motor dynamics are discussed. The results show that the traction motor is significantly affected by the train system, when the motor is equivalent to the bogie frame mass, the phenomenon of underestimation exists to evaluate the vibration of the motor. In addition, suspension parameters have a great impact on the traction motor dynamics, rational selection suspension parameters can help to attenuate the vibration of the traction motor, and alleviate uneven the distribution of the air gap magnetic field of the traction motor.

Effect of vehicle-track vertical coupling vibrations on frame-mounted traction motor dynamics

Highlights

A vehicle-track vertical coupling dynamic model with considering the influence of the frame-mounted traction motor is established.
The influences of the vehicle-track vertical coupling vibrations on the frame-mounted traction motor dynamics are discussed.
The influences of the suspension parameters on the vertical vibration responses of the frame-mounted traction motor dynamics are discussed.

1. Introduction

Finding out the vibration mechanism of each subsystem is the key to ensure the safety and smooth operation of trains, and is also the premise of the design of railway vehicles’ main components [1, 2]. Many scholars have carried out a lot of research around this. For example, Dimitriu [3] compared the vertical vibration of trains under the rigid and elastic carbody from the comfort perspective by establishing a vertical dynamic model of railway vehicles with considering the elastic deformation of the car body. Lu et al. [4] proposed a solution method of the vehicle-track vertical coupling dynamic model based on the symplectic method, and discussed the influence of the track damping and vehicle speed on the train vertical dynamic responses. Nagai et al. [5] studied the influence of the passenger number and the passenger distribution on the railway vehicle’s car body vibration by establishing a passenger-body coupling vibration analysis model. However, for trains driven by traction motors, due to the limitation of computer performance, most of the early studies on train’s dynamic performance based on multi-body dynamics always simplified the traction motor to the spring-up and/or spring-down mass. In fact, for railway vehicles with power bogie system, the traction motor and the train system are a coupling system [6, 7], therefore, when ignoring the coupling between the traction motor and the train system, it will inevitably affect the analysis results of the train system’s vibration response, and also cannot analyze the dynamic characteristics of the traction motor during train operation.

In recent years, with the continuous deepening of research, researchers in various countries have carried out many related studies on trains and traction motors [2]. Alfi et al. [8] analyzed the influence of the motor connection stiffness on the critical speed of railway vehicles, and used dynamic absorbers to explain the impact of the drive system elastic suspension on vehicle lateral stability. Yao et al. [9] discussed the mechanism of the impact of elastic suspension on locomotive dynamic performance. The results show that when the lateral suspension frequency of the drive system is close to the wheel-set rotational frequency, the locomotive has the best lateral dynamic performance. Besides, the small lateral suspension damping helps to improve the lateral stability of the locomotive and reduce the force of the wheel and the rail. Luo et al. [10] analyzed the influence of the suspension parameters of traction drive device on locomotive lateral dynamic performance. The results indicate that the mass of the traction drive device and the lateral stiffness of primary suspension have a great influence on the rigid suspension locomotive, but little influence on the elastic suspension locomotive. When locomotive’s running speed is above 160 km/h, the suspension mode of the traction device should adopt elastic suspension type. In addition, on the basis of considering the coupling vibration of the train system and the traction motor synthetically, Senini et al. [11] used computer to establish a dynamic simulation method for the wheel-rail interactions, and studied the impact of the wheel slip/rotation effect and the wheel diameter on the load of the motor. Zhai [12, 13] studied the vibration characteristics of the traction motor and the dynamic interaction between the locomotive and the track by establishing a locomotive-track vertical coupling dynamic model with considering the influence of the axle-mounted traction motor, and then, he used the model to calculate and compare the dynamic characteristics of the locomotive to the track under the rigid and elastic suspension modes of the axle-mounted traction motor, and studied the influence of the vehicle vibration on the dynamics of pantograph mounting system [14]. Chen et al. [15, 16] studied the effect of the locomotive dynamic characteristics on the root crack of the transmission system under traction drive conditions by establishing a heavy-haul electric locomotive-track vertical longitudinal coupling dynamic model with considering the dynamic effect of gear transmission. Liu et al. [17] analyzed the dynamic force of the wheel and the rail under curve driving conditions by using the locomotive-track vertical coupling dynamic model.

As stated above, although many scholars have done a lot of research on the dynamic characteristics of the train system and the traction motor under the coupling of the train and the motor, most of them are aimed at axle-mounted traction motor. Therefore, it is impossible to accurately describe the actual vibration of the train system and the traction motor under the influence of the frame-mounted traction motor. It shows that, the vertical coupling vibration mechanism between the frame-mounted traction motor and the train system needs to be further studied. In this paper, according to the structural characteristics of a train with frame-mounted traction motor, a vehicle-track vertical coupling dynamic model with considering the influence of the frame-mounted traction motor is established. Then, by considering both the track irregularity excitation and the traction motor vibration characteristics, the vertical vibration responses of the train with frame-mounted traction motor are simulated, and the correctness of the dynamic model established is verified by the real vehicle test. In case of the investigated vehicle model, the influences of the vehicle-track vertical coupling vibrations and the suspension parameters on the frame-mounted traction motor dynamics are discussed. The research made in this paper can provide an effective model reference for the analysis of the dynamic characteristics of the frame-mounted traction motor and the optimization design of the motor suspension parameters.

2. Vehicle-track vertical coupling dynamic model with considering the frame-mounted traction motor

2.1. Physical model of the vertical coupling system

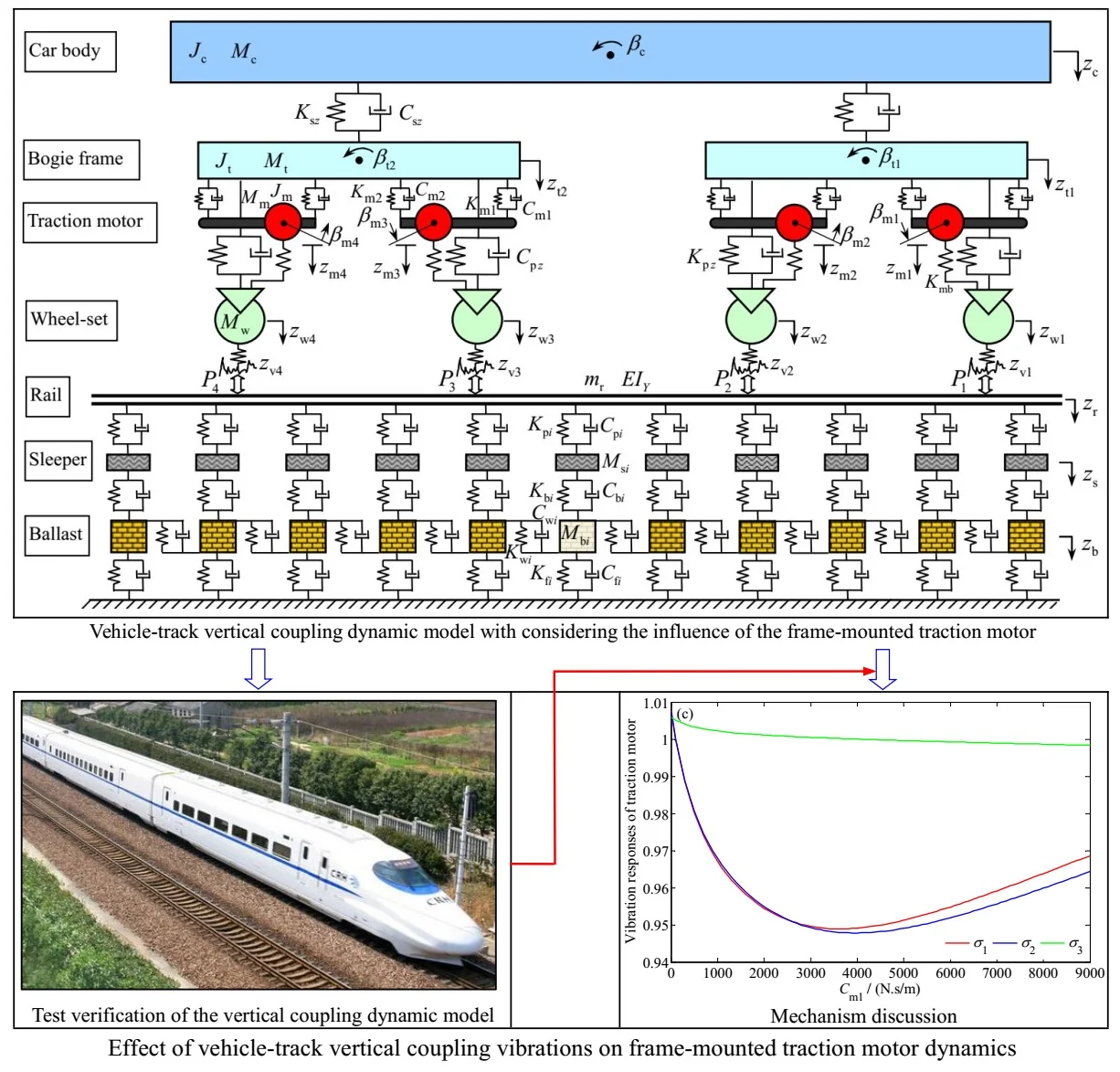
According to the actual structure of a train, the influence of the gear meshing in the transmission system and the radial clearance in the motor bearing are neglected, the effect of the lubricating oil film between the bearing inner/outer rings and the rolling body is not considered, and in the vertical direction, the bearing is equivalent to an elastic element, the motor is equivalent to a single mass spring-damping vibration system, a vehicle-track vertical coupling vibration dynamic model with considering the influence of the frame-mounted traction motor is established, as shown in Fig. 1. Here, $M_{c}$ , $M_{t}$ , $M_{w}$ , and $M_{m}$ are the half of the car body mass, the bogie frame mass, the wheel-set and motor rotor total mass, and the motor stator and the shell total mass, respectively; $J_{c}$ , $J_{t}$ , and $J_{m}$ are the half of the car body moment inertia, the frame moment inertia, and the motor stator and the shell total moment inertia, respectively; $C_{p z}$ and $C_{s z}$ are the vertical equivalent damping of one side of the primary suspension and secondary suspension, respectively; $K_{p z}$ and $K_{s z}$ are the vertical equivalent stiffness of one side of the primary suspension and secondary suspension, respectively; $C_{m 1}$ and $C_{m 2}$ are the damping between the frame and driving system, respectively; $K_{m 1}$ and $K_{m 2}$ are the stiffness between the frame and driving system, respectively; $K_{m b}$ is the equivalent stiffness of the bearing; $m_{r}$ , $M_{s i}$ , and $M_{b i}$ are the rail mass per unit length, the half of the sleeper mass, and the single side ballast mass, respectively; $I_{Y}$ is the rail section inertia, $E$ is the rail elastic modulus; $K_{p i}$ , $K_{b i}$ , $K_{w i}$ , and $K_{f i}$ are the rail pad stiffness, the ballast support stiffness, the ballast shear stiffness, and the subgrade support stiffness, respectively; $C_{p i}$ , $C_{b i}$ , $C_{w i}$ , and $C_{f i}$ are the rail pad damping, the ballast damping, the ballast shear damping, and the subgrade damping, respectively. In addition, $z_{c}$ , $z_{t 1}$ - $z_{t 2}$ , $z_{m 1}$ - $z_{m 4}$ , and $z_{w 1}$ - $z_{w 4}$ are the vertical displacements of the car body, the bogie frame, the traction motor, and the wheel-set, respectively; $β_{c}$ , $β_{t 1}$ - $β_{t 2}$ , and $β_{m 1}$ - $β_{m 4}$ are the pitch displacements of the car body, the bogie frame, and the traction motor, respectively; $z_{r}$ , $z_{s}$ , and $z_{b}$ are the vertical displacements of the rail, the sleeper, and the ballast, respectively. $P_{1}$ - $P_{4}$ are the wheel-rail forces; $z_{v 1}$ - $z_{v 4}$ are the track irregularities of each wheel-set, and $z_{v 2} = z_{v 1} (t - τ_{1})$ , $z_{v 3} = z_{v 1} (t - τ_{2})$ , $z_{v 4} = z_{v 1} (t - τ_{3})$ , where, $t$ denotes time, $τ$ is the time lag, $τ_{1} = 2 L_{t} / v$ , $τ_{2} = 2 L_{c} / v$ , $τ_{3} = 2 (L_{t} + L_{c}) / v$ , $L_{c}$ and $L_{t}$ are the half distances of the vehicle spacing and the bogie wheelbase, respectively, $v$ is the train running speed.

Fig. 1Vehicle-track vertical coupling dynamic model with considering the influence of the frame-mounted traction motor

2.2. Mathematical model of the vertical coupling system

According to the Newton’s second law and the Elastic vibration theory, the vibration differential equations of each subsystem in the model shown in Fig. 1 can be derived as follows:

– Vertical vibration of the car body:

1

M_{c} {\ddot{z}}_{c} = - K_{s z} (z_{c} - L_{c} β_{c} - z_{t 1}) - C_{s z} ({\dot{z}}_{c} - L_{c} {\dot{β}}_{c} - {\dot{z}}_{t 1})

- K_{s z} (z_{c} + L_{c} β_{c} - z_{t 2}) - C_{s z} ({\dot{z}}_{c} + L_{c} {\dot{β}}_{c} - {\dot{z}}_{t 2}) .

– Pitching vibration of the car body:

2

J_{c} {\ddot{β}}_{c} = [K_{s z} (z_{c} - L_{c} β_{c} - z_{t 1}) + C_{s z} ({\dot{z}}_{c} - L_{c} {\dot{β}}_{c} - {\dot{z}}_{t 1})

- K_{s z} (z_{c} + L_{c} β_{c} - z_{t 2}) - C_{s z} ({\dot{z}}_{c} + L_{c} {\dot{β}}_{c} - {\dot{z}}_{t 2})] L_{c} .

Vertical vibration of the front bogie frame:

3

M_{t} {\ddot{z}}_{t 1} = - K_{p z} (z_{t 1} + L_{t} β_{t 1} - z_{w 2}) - C_{p z} ({\dot{z}}_{t 1} + L_{t} {\dot{β}}_{t 1} - {\dot{z}}_{w 2})

- K_{m 1} (z_{t 1} - L_{b} β_{t 1} - z_{m 1} + L_{1} β_{m 1}) - K_{p z} (z_{t 1} - L_{t} β_{t 1} - z_{w 1})

- C_{m 1} ({\dot{z}}_{t 1} - L_{b} {\dot{β}}_{t 1} - {\dot{z}}_{m 1} + L_{1} {\dot{β}}_{m 1}) - C_{p z} ({\dot{z}}_{t 1} - L_{t} {\dot{β}}_{t 1} - {\dot{z}}_{w 1})

- C_{s z} ({\dot{z}}_{t 1} - {\dot{z}}_{c} + L_{c} {\dot{β}}_{c}) - K_{m 2} [z_{t 1} - (L_{b} - L_{1} - L_{2}) β_{t 1} - z_{m 1} - L_{2} β_{m 1}]

- C_{m 2} [{\dot{z}}_{t 1} - (L_{b} - L_{1} - L_{2}) {\dot{β}}_{t 1} - {\dot{z}}_{m 1} - L_{2} {\dot{β}}_{m 1}]

- K_{m 2} [z_{t 1} + (L_{b} - L_{1} - L_{2}) β_{t 1} - z_{m 2} + L_{2} β_{m 2}]

- C_{m 2} [{\dot{z}}_{t 1} + (L_{b} - L_{1} - L_{2}) {\dot{β}}_{t 1} - {\dot{z}}_{m 2} + L_{2} {\dot{β}}_{m 2}]

- K_{m 1} (z_{t 1} + L_{b} β_{t 1} - z_{m 2} - L_{1} β_{m 2}) - K_{s z} (z_{t 1} - z_{c} + L_{c} β_{c})

- C_{m 1} ({\dot{z}}_{t 1} + L_{b} {\dot{β}}_{t 1} - {\dot{z}}_{m 2} - L_{1} {\dot{β}}_{m 2}) .

– Pitching vibration of the front bogie frame:

4

J_{t} {\ddot{β}}_{t 1} = K_{p z} (z_{t 1} - L_{t} β_{t 1} - z_{w 1}) L_{t} + C_{p z} ({\dot{z}}_{t 1} - L_{t} {\dot{β}}_{t 1} - {\dot{z}}_{w 1}) L_{t}

- K_{p z} (z_{t 1} + L_{t} β_{t 1} - z_{w 2}) L_{t} - C_{p z} ({\dot{z}}_{t 1} + L_{t} {\dot{β}}_{t 1} - {\dot{z}}_{w 2}) L_{t}

+ K_{m 1} (z_{t 1} - L_{b} β_{t 1} - z_{m 1} + L_{1} β_{m 1}) L_{b} + C_{m 1} ({\dot{z}}_{t 1} - L_{b} {\dot{β}}_{t 1} - {\dot{z}}_{m 1} + L_{1} {\dot{β}}_{m 1}) L_{b}

- K_{m 1} (z_{t 1} + L_{b} β_{t 1} - z_{m 2} - L_{1} β_{m 2}) L_{b} - C_{m 1} ({\dot{z}}_{t 1} + L_{b} {\dot{β}}_{t 1} - {\dot{z}}_{m 2} - L_{1} {\dot{β}}_{m 2}) L_{b}

+ K_{m 2} [z_{t 1} - (L_{b} - L_{1} - L_{2}) β_{t 1} - z_{m 1} - L_{2} β_{m 1}] (L_{b} - L_{1} - L_{2})

+ C_{m 2} [{\dot{z}}_{t 1} - (L_{b} - L_{1} - L_{2}) {\dot{β}}_{t 1} - {\dot{z}}_{m 1} - L_{2} {\dot{β}}_{m 1}] (L_{b} - L_{1} - L_{2})

- K_{m 2} [z_{t 1} + (L_{b} - L_{1} - L_{2}) β_{t 1} - z_{m 2} + L_{2} β_{m 2}] (L_{b} - L_{1} - L_{2})

- C_{m 2} [{\dot{z}}_{t 1} + (L_{b} - L_{1} - L_{2}) {\dot{β}}_{t 1} - {\dot{z}}_{m 2} + L_{2} {\dot{β}}_{m 2}] (L_{b} - L_{1} - L_{2}) .

– Vertical vibration of the rear bogie frame:

5

M_{t} {\ddot{z}}_{t 2} = - K_{p z} (z_{t 2} - L_{t} β_{t 2} - z_{w 3}) - C_{p z} ({\dot{z}}_{t 2} - L_{t} {\dot{β}}_{t 2} - {\dot{z}}_{w 3})

- K_{m 1} (z_{t 2} - L_{b} β_{t 2} - z_{m 3} + L_{1} β_{m 3}) - K_{p z} (z_{t 2} + L_{t} β_{t 2} - z_{w 4})

- C_{m 1} ({\dot{z}}_{t 2} - L_{b} {\dot{β}}_{t 2} - {\dot{z}}_{m 3} + L_{1} {\dot{β}}_{m 3}) - C_{p z} ({\dot{z}}_{t 2} + L_{t} {\dot{β}}_{t 2} - {\dot{z}}_{w 4})

- K_{m 2} [z_{t 2} - (L_{b} - L_{1} - L_{2}) β_{t 2} - z_{m 3} - L_{2} β_{m 3}]

- C_{m 2} [{\dot{z}}_{t 2} - (L_{b} - L_{1} - L_{2}) {\dot{β}}_{t 2} - {\dot{z}}_{m 3} - L_{2} {\dot{β}}_{m 3}]

- K_{m 2} [z_{t 2} + (L_{b} - L_{1} - L_{2}) β_{t 2} - z_{m 4} + L_{2} β_{m 4}]

- C_{m 2} [{\dot{z}}_{t 2} + (L_{b} - L_{1} - L_{2}) {\dot{β}}_{t 2} - {\dot{z}}_{m 4} + L_{2} {\dot{β}}_{m 4}]

- K_{m 1} (z_{t 2} + L_{b} β_{t 2} - z_{m 4} - L_{1} β_{m 4}) - K_{s z} (z_{t 2} - z_{c} - L_{c} β_{c})

- C_{s z} ({\dot{z}}_{t 2} - {\dot{z}}_{c} - L_{c} {\dot{β}}_{c}) - C_{m 1} ({\dot{z}}_{t 2} + L_{b} {\dot{β}}_{t 2} - {\dot{z}}_{m 4} - L_{1} {\dot{β}}_{m 4}) .

– Pitching vibration of the rear bogie frame:

6

J_{t} {\ddot{β}}_{t 2} = K_{p z} (z_{t 2} - L_{t} β_{t 2} - z_{w 3}) L_{t} + C_{p z} ({\dot{z}}_{t 2} - L_{t} {\dot{β}}_{t 2} - {\dot{z}}_{w 3}) L_{t}

- K_{p z} (z_{t 2} + L_{t} β_{t 2} - z_{w 4}) L_{t} - C_{p z} ({\dot{z}}_{t 2} + L_{t} {\dot{β}}_{t 2} - {\dot{z}}_{w 4}) L_{t}

+ K_{m 1} (z_{t 2} - L_{b} β_{t 2} - z_{m 3} + L_{1} β_{m 3}) L_{b} + C_{m 1} ({\dot{z}}_{t 2} - L_{b} {\dot{β}}_{t 2} - {\dot{z}}_{m 3} + L_{1} {\dot{β}}_{m 3}) L_{b}

- K_{m 1} (z_{t 2} + L_{b} β_{t 2} - z_{m 4} - L_{1} β_{m 4}) L_{b} - C_{m 1} ({\dot{z}}_{t 2} + L_{b} {\dot{β}}_{t 2} - {\dot{z}}_{m 4} - L_{1} {\dot{β}}_{m 4}) L_{b}

+ K_{m 2} [z_{t 2} - (L_{b} - L_{1} - L_{2}) β_{t 2} - z_{m 3} - L_{2} β_{m 3}] (L_{b} - L_{1} - L_{2})

+ C_{m 2} [{\dot{z}}_{t 2} - (L_{b} - L_{1} - L_{2}) {\dot{β}}_{t 2} - {\dot{z}}_{m 3} - L_{2} {\dot{β}}_{m 3}] (L_{b} - L_{1} - L_{2})

- K_{m 2} [z_{t 2} + (L_{b} - L_{1} - L_{2}) β_{t 2} - z_{m 4} + L_{2} β_{m 4}] (L_{b} - L_{1} - L_{2})

- C_{m 2} [{\dot{z}}_{t 2} + (L_{b} - L_{1} - L_{2}) {\dot{β}}_{t 2} - {\dot{z}}_{m 4} + L_{2} {\dot{β}}_{m 4}] (L_{b} - L_{1} - L_{2}) .

– Vertical vibration of the first wheel-set:

7

M_{w} {\ddot{z}}_{w 1} = - K_{p z} (z_{w 1} - z_{t 1} + L_{t} β_{t 1}) - C_{p z} ({\dot{z}}_{w 1} - {\dot{z}}_{t 1} + L_{t} {\dot{β}}_{t 1})

- K_{m b} (z_{w 1} - z_{m 1}) - K_{H} (z_{w 1} - z_{v 1}) - P_{1} (t) + P_{0} .

– Vertical vibration of the second wheel-set:

8

M_{w} {\ddot{z}}_{w 2} = - K_{p z} (z_{w 2} - z_{t 1} - L_{t} β_{t 1}) - C_{p z} ({\dot{z}}_{w 2} - {\dot{z}}_{t 1} - L_{t} {\dot{β}}_{t 1})

- K_{m b} (z_{w 2} - z_{m 2}) - K_{H} (z_{w 2} - z_{v 2}) - P_{2} (t) + P_{0} .

– Vertical vibration of the third wheel-set:

9

M_{w} {\ddot{z}}_{w 3} = - K_{p z} (z_{w 3} - z_{t 2} + L_{t} β_{t 2}) - C_{p z} ({\dot{z}}_{w 3} - {\dot{z}}_{t 2} + L_{t} {\dot{β}}_{t 2})

- K_{m b} (z_{w 3} - z_{m 3}) - K_{H} (z_{w 3} - z_{v 3}) - P_{3} (t) + P_{0} .

– Vertical vibration of the forth wheel-set:

10

M_{w} {\ddot{z}}_{w 4} = - K_{p z} (z_{w 4} - z_{t 2} - L_{t} β_{t 2}) - C_{p z} ({\dot{z}}_{w 4} - {\dot{z}}_{t 2} - L_{t} {\dot{β}}_{t 2})

- K_{m b} (z_{w 4} - z_{m 4}) - K_{H} (z_{w 4} - z_{v 4}) - P_{4} (t) + P_{0} .

– Vertical vibration of the first traction motor:

11

M_{m} {\ddot{z}}_{m 1} = - K_{m 1} (z_{m 1} - L_{1} β_{m 1} - z_{t 1} + L_{b} β_{t 1})

- K_{m 2} [z_{m 1} + L_{2} β_{m 1} - z_{t 1} + (L_{b} - L_{1} - L_{2}) β_{t 1}] - K_{m b} (z_{m 1} - z_{w 1})

- C_{m 2} [{\dot{z}}_{m 1} + L_{2} {\dot{β}}_{m 1} - {\dot{z}}_{t 1} + (L_{b} - L_{1} - L_{2}) {\dot{β}}_{t 1}]

- C_{m 1} ({\dot{z}}_{m 1} - L_{1} {\dot{β}}_{m 1} - {\dot{z}}_{t 1} + L_{b} {\dot{β}}_{t 1}) + M_{m} e ω^{2} c o s (ω t) .

– Pitching vibration of the first traction motor:

12

J_{m} {\ddot{β}}_{m 1} = K_{m 1} (z_{m 1} - L_{1} β_{m 1} - z_{t 1} + L_{b} β_{t 1}) L_{1} + C_{m 1} ({\dot{z}}_{m 1} - L_{1} {\dot{β}}_{m 1} - {\dot{z}}_{t 1} + L_{b} {\dot{β}}_{t 1}) L_{1}

- K_{m 2} [z_{m 1} + L_{2} β_{m 1} - z_{t 1} + (L_{b} - L_{1} - L_{2}) β_{t 1}] L_{2}

- C_{m 2} [{\dot{z}}_{m 1} + L_{2} {\dot{β}}_{m 1} - {\dot{z}}_{t 1} + (L_{b} - L_{1} - L_{2}) {\dot{β}}_{t 1}] L_{2} .

– Vertical vibration of the second traction motor:

13

M_{m} {\ddot{z}}_{m 2} = - K_{m 1} (z_{m 2} + L_{1} β_{m 2} - z_{t 1} - L_{b} β_{t 1})

- K_{m 2} [z_{m 2} - L_{2} β_{m 2} - z_{t 1} - (L_{b} - L_{1} - L_{2}) β_{t 1} - K_{m b} (z_{m 2} - z_{w 2})]

- C_{m 2} [{\dot{z}}_{m 2} - L_{2} {\dot{β}}_{m 2} - {\dot{z}}_{t 1} - (L_{b} - L_{1} - L_{2}) {\dot{β}}_{t 1}]

- C_{m 1} ({\dot{z}}_{m 2} + L_{1} {\dot{β}}_{m 2} - {\dot{z}}_{t 1} - L_{b} {\dot{β}}_{t 1}) + M_{m} e ω^{2} c o s (ω t) .

– Pitching vibration of the second traction motor:

14

J_{m} {\ddot{β}}_{m 2} = - K_{m 1} (z_{m 2} + L_{1} β_{m 2} - z_{t 1} - L_{b} β_{t 1}) L_{1}

+ C_{m 2} [{\dot{z}}_{m 2} - L_{2} {\dot{β}}_{m 2} - {\dot{z}}_{t 1} - (L_{b} - L_{1} - L_{2}) {\dot{β}}_{t 1}] L_{2}

+ K_{m 2} [z_{m 2} - L_{2} β_{m 2} - z_{t 1} - (L_{b} - L_{1} - L_{2}) β_{t 1}] L_{2}

- C_{m 1} ({\dot{z}}_{m 2} + L_{1} {\dot{β}}_{m 2} - {\dot{z}}_{t 1} - L_{b} {\dot{β}}_{t 1}) L_{1} .

– Vertical vibration of the third traction motor:

15

M_{m} {\ddot{z}}_{m 3} = - K_{m 1} (z_{m 3} - L_{1} β_{m 3} - z_{t 2} + L_{b} β_{t 2})

- K_{m 2} [z_{m 3} + L_{2} β_{m 3} - z_{t 2} + (L_{b} - L_{1} - L_{2}) β_{t 2}] - K_{m b} (z_{m 3} - z_{w 1})

- C_{m 2} [{\dot{z}}_{m 3} + L_{2} {\dot{β}}_{m 3} - {\dot{z}}_{t 2} + (L_{b} - L_{1} - L_{2}) {\dot{β}}_{t 2}]

- C_{m 1} ({\dot{z}}_{m 3} - L_{1} {\dot{β}}_{m 3} - {\dot{z}}_{t 2} + L_{b} {\dot{β}}_{t 2}) + M_{m} e ω^{2} c o s (ω t) .

– Pitching vibration of the third traction motor:

16

J_{m} {\ddot{β}}_{m 3} = K_{m 1} (z_{m 3} - L_{1} β_{m 3} - z_{t 2} + L_{b} β_{t 2}) L_{1}

- C_{m 2} [{\dot{z}}_{m 3} + L_{2} {\dot{β}}_{m 3} - {\dot{z}}_{t 2} + (L_{b} - L_{1} - L_{2}) {\dot{β}}_{t 2}] L_{2}

- K_{m 2} [z_{m 3} + L_{2} β_{m 3} - z_{t 2} + (L_{b} - L_{1} - L_{2}) β_{t 2}] L_{2}

+ C_{m 1} ({\dot{z}}_{m 3} - L_{1} {\dot{β}}_{m 3} - {\dot{z}}_{t 2} + L_{b} {\dot{β}}_{t 2}) L_{1} .

– Vertical vibration of the forth traction motor:

17

M_{m} {\ddot{z}}_{m 4} = - K_{m 1} (z_{m 4} + L_{1} β_{m 4} - z_{t 2} - L_{b} β_{t 2})

- K_{m 2} [z_{m 4} - L_{2} β_{m 4} - z_{t 2} - (L_{b} - L_{1} - L_{2}) β_{t 2}] - K_{m b} (z_{m 4} - z_{w 4})

- C_{m 2} [{\dot{z}}_{m 4} - L_{2} {\dot{β}}_{m 4} - {\dot{z}}_{t 2} - (L_{b} - L_{1} - L_{2}) {\dot{β}}_{t 2}]

- C_{m 1} ({\dot{z}}_{m 4} + L_{1} {\dot{β}}_{m 4} - {\dot{z}}_{t 2} - L_{b} {\dot{β}}_{t 2}) + M_{m} e ω^{2} c o s (ω t) .

– Pitching vibration of the forth traction motor:

18

J_{m} {\ddot{β}}_{m 4} = - K_{m 1} (z_{m 4} + L_{1} β_{m 4} - z_{t 2} - L_{b} β_{t 2}) L_{1}

+ K_{m 2} [z_{m 4} - L_{2} β_{m 4} - z_{t 2} - (L_{b} - L_{1} - L_{2}) β_{t 2}] L_{2}

- C_{m 1} ({\dot{z}}_{m 4} + L_{1} {\dot{β}}_{m 4} - {\dot{z}}_{t 2} - L_{b} {\dot{β}}_{t 2}) L_{1} + C_{m 2} [{\dot{z}}_{m 4} - L_{2} {\dot{β}}_{m 4} - {\dot{z}}_{t 2} - (L_{b} - L_{1} - L_{2}) {\dot{β}}_{t 2}] L_{2} .

– Vertical vibration of the rail:

19

{\ddot{q}}_{k} (t) = - \sum_{i = 1}^{N} C_{p i} z_{k} (x_{i}) \sum_{h = 1}^{N M} z_{h} (x_{i}) {\dot{q}}_{h} (t) - \frac{E I_{Y}}{m_{r}} {(\frac{k π}{L})}^{4} q_{k} (t)

- \sum_{i = 1}^{N} K_{p i} z_{k} (x_{i}) \sum_{h = 1}^{N M} z_{h} (x_{i}) q_{h} (t) + \sum_{i = 1}^{N} C_{p i} z_{k} (x_{i}) {\dot{z}}_{s i} (t)

+ \sum_{i = 1}^{N} K_{p i} z_{k} (x_{i}) z_{s i} (t) + \sum_{n = 1}^{4} P_{n} (t) z_{k} (x_{w n}), （k = 1, \dots, N M） .

– Vertical vibration of the sleeper:

20

M_{s i} {\ddot{z}}_{s i} (t) = - (C_{p i} + C_{b i}) {\dot{z}}_{s i} (t) - (K_{p i} + K_{b i}) z_{s i} (t) + C_{b i} {\dot{z}}_{b i} (t) + K_{b i} z_{b i} (t)

+ C_{p i} \sum_{h = 1}^{N M} z_{h} (x_{i}) {\dot{q}}_{h} (t) + K_{p i} \sum_{h = 1}^{N M} z_{h} (x_{i}) q_{h} (t), （i = 1, \dots, N） .

– Vertical vibration of the ballast:

21

M_{b i} {\ddot{z}}_{b i} (t) = C_{b i} {\dot{z}}_{s i} (t) + K_{b i} z_{s i} (t) + C_{w i} {\dot{z}}_{b (i + 1)} (t) - (C_{b i} + C_{f i} + 2 C_{w i}) {\dot{z}}_{b i} (t)

- K_{w i} z_{b (i + 1)} (t) + C_{w i} {\dot{z}}_{b (i - 1)} (t) - (K_{b i} + K_{f i} + 2 K_{w i}) z_{b i} (t) + K_{w i} z_{b (i - 1)} (t),

（i = 1, \dots, N） .

Here, $L_{1}$ is the distance between the driving system mass center and the end beam suspension point, $L_{2}$ is the distance between the driving system mass center and the crossbeam suspension point, $L_{b}$ is the half of the frame length, $e$ is the rotor eccentricity, $ω$ is the speed of the rotor. $P_{0}$ is the static force of the wheel and the rail, $P_{n} (t)$ is the vertical force of the wheel and the rail, $N M$ is the rail modal order, $N$ is the sleeper number; $q_{k} (t)$ is the regular vibration mode coordinate of the rail, in which $k$ is the mode order number; $z_{h} (x_{i})$ is the transposed matrix of $z_{k} (x_{i})$ ; the expression of $z_{k} (x_{i})$ and $P_{n} (t)$ can be written as [18]:

z_{k} (x) = \sqrt{\frac{2}{m_{r} L}} s i n \frac{k π x}{L},

P_{n} (t) = \{\begin{array}{l} {\{\frac{1}{G} [z_{w n} (t) - z_{r} (x_{w n}, t) - z_{v n} (t)]\}}^{3 / 2}, z_{w n} (t) - z_{r} (x_{w n}, t) - z_{v n} (t) \geq 0, \\ 0, z_{w n} (t) - z_{r} (x_{w n}, t) - z_{v n} (t) < 0, \end{array}

where, $G$ is the contact constant of the wheel and the rail, for the taper tread wheel $G =$ 4.57 $R$ ^-0.149×10^-8 (m/N^2/3), for the wear type tread wheel $G =$ 3.86 $R$ ^-0.115×10^-8 (m/N^2/3), $R$ is the wheel radius.

2.3. Numerical solution of the system dynamic response

By analyzing the mathematical model of the vertical coupling system, it can be seen that, the equation group is a large, complex nonlinear dynamic differential equation group (with 18+ $N M$ +2 $N$ DOFs). It is difficult to solve it by the analytic method. Therefore, we need to use numerical integration method to solve it. According to Eqs. (1-21), they can be expressed as the following matrix and vector form:

22

M \{\ddot{X}\} + C \{\dot{X}\} + K \{X\} = \{P\},

where, $M$ , $C$ , and $K$ are the mass, damping, and stiffness matrices of the vertical coupling system, respectively; ${\ddot{X}}$ , ${\dot{X}}$ , and { $X$ } are the generalized acceleration, velocity, and displacement vectors, respectively; { $P$ } is the force vector.

According to Eq. (22), using the Newmark- $β$ implicit integration algorithm, the time-domain responses of the vehicle-track vertical coupling vibration dynamic model with considering the influence of the frame-mounted traction motor can be calculated. The iterative process of solving the equation is as follows:

{X}_{m} = \frac{K + \frac{M}{γ Δ t^{2}} + \frac{β C}{γ Δ t}}{(\begin{array}{l} \{{P}_{m - 1} + M [\frac{{X}_{m - 1}}{γ Δ t^{2}} + \frac{{V}_{m - 1}}{γ Δ t} + (1 - 2 γ) \frac{{A}_{m - 1}}{2 γ}] \\ + C [β \frac{{X}_{m - 1}}{γ Δ t} + (β - γ) \frac{{V}_{m - 1}}{γ} + (β - 2 γ) \frac{{A}_{m - 1} Δ t}{2 γ}]\} \end{array})},

{A}_{m} = \frac{[{X}_{m} - {X}_{m - 1}]}{γ Δ t^{2}} - \frac{{V}_{m - 1}}{γ Δ t} - (1 - 2 γ) \frac{{A}_{m - 1}}{2 γ},

{V}_{m} = {V}_{m - 1} + (1 - β) {A}_{m - 1} Δ t + β {A}_{m} Δ t,

where, $Δ t$ is the time integration step, $m$ represents the iterative step; $β$ and $γ$ are the parameters to control the accuracy and stability of the integration method.

3. Test verification of the vertical coupling dynamic model

In order to verify the correctness of the vertical coupling dynamic model, the field measurements have been made by Shandong Zhiheng Vibration Damping Tech Co., Ltd, on a high-speed train which has been widely employed in China, and the analysis and test results are compared and analyzed. The wheel tread type of the train is wear type. The parameters of the traction motor and the train system can be found in Table 1, and the parameters of the ballasted track employed in this paper can be referenced to Zhai et al. [19]. The train running speed is 200 km/h, the corresponding motor rotor speed is 392 r/s, the eccentricity of the rotor is 1.5×10^-4 m, and the sampling frequency is 1 000 Hz.

Table 1System parameters values

Symbol	Unit	Value	Symbol	Unit	Value
$M_{c}$	kg	17 000	$K_{p z}$	N/m	275 000
$M_{t}$	kg	1 500	$K_{s z}$	N/m	200 000
$M_{w}$	kg	700	$K_{m b}$	N/m	1.0×10⁴
$M_{m}$	kg	220	$K_{m 1}$	N/m	1.0×10⁶
$J_{c}$	kg·m²	1 138 500	$K_{m 2}$	N/m	1.0×10⁶
$J_{t}$	kg·m²	1 355	$L_{c}$	m	9.0
$J_{m}$	kg·m²	13.7	$L_{t}$	m	1.2
$C_{p z}$	N·s/m	30 000	$L_{1}$	m	0.3
$C_{s z}$	N·s/m	40 000	$L_{2}$	m	0.5
$C_{m 1}$	N·s/m	100	$L_{b}$	m	1.8
$C_{m 2}$	N·s/m	100	$R$	m	0.457 5

Track irregularity is the excitation source of the wheel-rail system and the main cause of the vehicle vibration and wheel-rail force. It has an important impact on the dynamic characteristics of railway vehicles [20, 21]. Among them, the track vertical irregularity is the main cause of the trains’ vertical vibration. In order to make the simulation conditions as consistent as possible with the line conditions in the real vehicle test, the German track spectrum is adopted for the track irregularity. Since the track irregularity is usually expressed in the form of power spectral density, the time-frequency conversion method provided by Zhai et al. [19] is used to transform the track irregularity into a time-domain sample as the input of the system, and the vertical vibration responses of the train system and the traction motor are analyzed. Here, the spatial frequency analytical expression of the power spectral density of the track vertical irregularity is [22]:

23

S_{v} (Ω) = \frac{A_{v} Ω_{c}^{2}}{(Ω^{2} + Ω_{r}^{2}) (Ω^{2} + Ω_{c}^{2})},

where, $S_{v} (Ω)$ is the power spectral density of the track vertical irregularity, $Ω$ is the spatial frequency of the track irregularity, $A_{v}$ is the roughness coefficient of the rail; $Ω_{c}$ and $Ω_{r}$ are the truncated space frequencies. Each known parameter value is shown in Table 2. Here, the low interference spectrum is suitable for the vehicle speed of greater than or equal to 250 km/h, the high interference spectrum is suitable for the vehicle speed below 250 km/h.

Table 2Parameters of the track vertical irregularity

Track level	Parameter
Track level	$A_{v}$ /(m²·rad/m)	$Ω_{c}$ /(rad/m)	$Ω_{r}$ /(rad/m)
Low interference	4.032×10^-7	0.824 6	0.020 6
High interference	10.8×10^-7	0.824 6	0.020 6

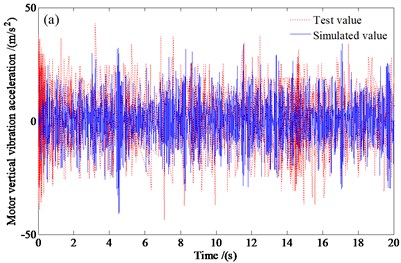
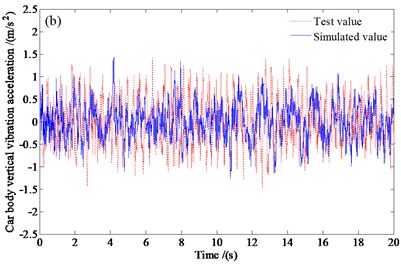
Fig. 2 shows the simulation analysis and test results of the vertical vibration accelerations of the traction motor and the car body, respectively.

From Fig. 2, it can be seen that, the vertical vibration acceleration responses of the traction motor and the car body calculated by simulation are in good agreement with the vibration responses measured by the actual vehicle test, but the peak values are slightly smaller than the measured results. In which, the maximum values of the vertical vibration accelerations of the traction motor and the car body simulated are 41.157 m/s² and 1.429 m/s², respectively, and the measured maximum values are 43.661 m/s² and 1.479 m/s², respectively. Thus, the vertical vibration accelerations of the traction motor and the car body calculated by the dynamic model established in this paper are in good agreement with the measured data, which shows that the vehicle-track vertical coupling vibration dynamic model with considering the influence of the frame-mounted traction motor proposed is correct.

Fig. 2Vertical random vibration response of the railway vehicle: a) the vertical vibration acceleration of the traction motor, b) the vertical vibration acceleration of the car body

Vertical random vibration response of the railway vehicle: a) the vertical vibration acceleration of the traction motor, b) the vertical vibration acceleration of the car body

4. The influence of the vehicle-track vertical coupling vibrations on the frame-mounted traction motor dynamics

In order to find out the influences of the vehicle-track vertical coupling vibrations on the frame-mounted traction motor dynamics, by using the dynamic model established in Section 2, taking the high-speed train described in Section 3 as an example, the vertical vibration responses of the train with or without frame-mounted traction motor under the excitation of track irregularity shown in Eq. (23) are analyzed. In which, the simulation time step is 0.002 s, the simulation time is 10 s, and the train speed is 250 km/h. In addition, in the process of simulation calculation, except the traction motor, other dynamic parameters and line parameters of the train are identical.

4.1. Influence of train system on the vibration response of the traction motor

Figs. 3-4 show the power spectral density curves of the vertical and pitching accelerations of the traction motor, and the relative clearance between the stator and rotor of the motor with or without the train system obtained by simulation. Since the similarity of the vibration laws of the four motors, only the analysis results of the first motor are given here. Note that, the influence of the random track irregularity disturbance is neglected when the train system is not considered.

Fig. 3Power spectral density curve of the traction motor vibration acceleration: a) the vertical acceleration of the traction motor, b) the pitching acceleration of the traction motor

Power spectral density curve of the traction motor vibration acceleration: a) the vertical acceleration of the traction motor, b) the pitching acceleration of the traction motor

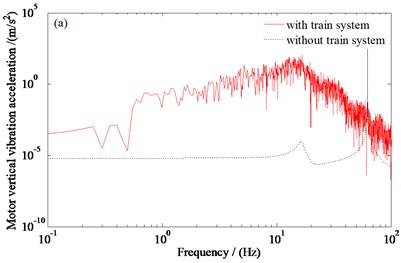
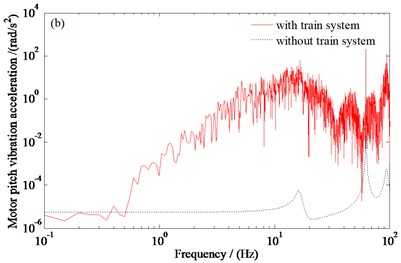
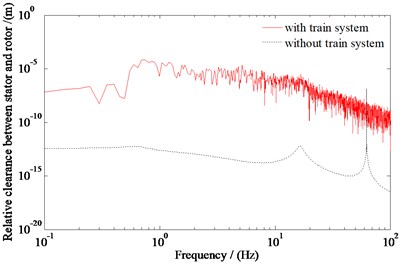
Fig. 3 and Fig. 4 show that, the vertical vibration responses of the traction motor increase significantly after considering the train system. When considering the train system, the root mean square values of the vertical and pitching vibration accelerations of the traction motor are 23.095 m/s² and 23.121 rad/s², respectively; the root mean square value of the relative clearance between the stator and rotor of the motor is 7.650×10^-3 m. When the train system is not considered, the root mean square values of the vertical and pitching vibration accelerations of the traction motor are 17.185 m/s² and 17.185 rad/s², respectively; the root mean square value of the relative clearance between the stator and rotor of the motor is 1.013×10^-4 m. The results show that the traction motor is significantly affected by the train system. Therefore, the influence of the train system should be taken into account when analyzing the vibration characteristics of the traction motor.

Fig. 4Power spectral density curve of the relative clearance between the stator and rotor

4.2. Influence of electromechanical coupling on the vibration response of the traction motor

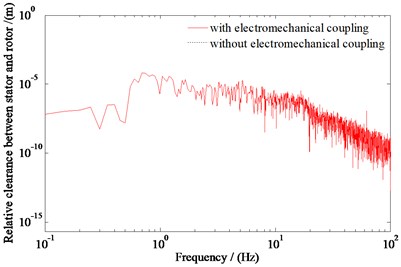
Fig. 5 and Fig. 6 show the power spectral density curves of the vertical and pitching acceleration of the traction motor, and the relative clearance between the stator and rotor of the motor with or without the electromechanical coupling obtained by simulation. Since the similarity of the vibration laws of the four motors, only the analysis results of the first motor are given here. Here, when the electromechanical coupling is not considered, the motor is equivalent to the frame mass.

Fig. 5Power spectral density curve of the traction motor vibration acceleration: a) the vertical acceleration of the traction motor, b) the pitching acceleration of the traction motor

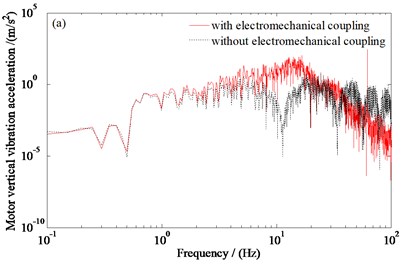
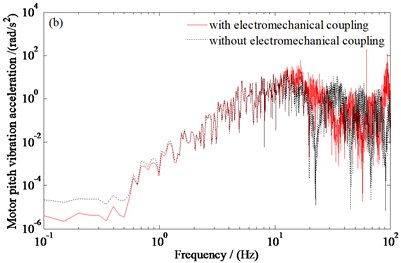
From Fig. 5 and Fig. 6, it can be seen that, the vertical vibration responses of the traction motor increases with considering the electromechanical coupling. When considering the electromechanical coupling, the root mean square values of the vertical and pitching vibration accelerations of the traction motor are 23.095 m/s² and 23.121 rad/s², respectively; the root mean square value of the relative clearance between the stator and rotor of the motor is 7.650×10^-3 m. When the electromechanical coupling is not considered, the root mean square values of the vertical and pitching vibration accelerations of the traction motor are 22.579 m/s² and 21.761 rad/s², respectively; the root mean square value of the relative clearance between the stator and rotor of the motor is 0 m. The results show that when the motor is equivalent to the bogie frame mass, the phenomenon of underestimation exists to evaluate the vibration of the motor. Therefore, the coupling effect between the train system and the traction motor should be considered in the analysis of the vibration characteristics of the motor.

Fig. 6Power spectral density curve of the relative clearance between the stator and rotor

5. The influence of the suspension parameters on the frame-mounted traction motor dynamics

In order to find out the influences of the suspension parameters on the frame-mounted traction motor dynamics, taking the high-speed train described in Section 3 as an example, the influences of the stiffness parameters $K_{m 1}$ , $K_{m 2}$ and damping parameters $C_{m 1}$ and $C_{m 2}$ on the vibration responses of the traction motor are studied by using the coupling system model.

Fig. 7The influences of the suspension parameters on the vibration responses of the traction motor: a) the influence of Km1, b) the influence of Km2, c) the influence of Cm1, d) the influence of Cm2

The influences of the suspension parameters on the vibration responses of the traction motor: a) the influence of Km1, b) the influence of Km2, c) the influence of Cm1, d) the influence of Cm2

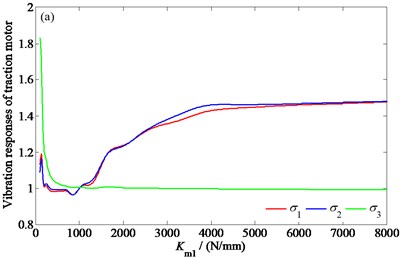
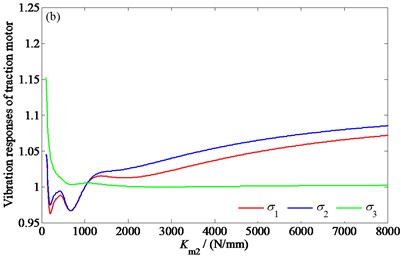
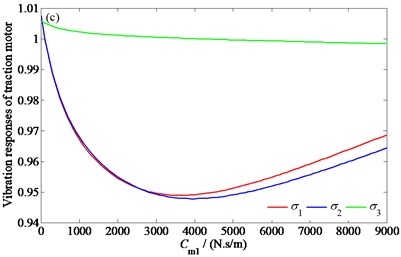
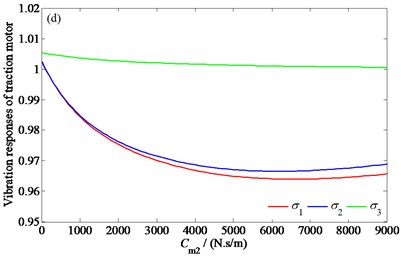
Fig. 7 shows the change of the root mean square values of the vertical and pitching vibration accelerations of the traction motor, and the relative clearance between the motor stator and rotor with the stiffness parameters $K_{m 1}$ , $K_{m 2}$ and damping parameters $C_{m 1}$ and $C_{m 2}$ , respectively. In order to represent each response in a same figure, ${\ddot{z}}_{m 1}$ , ${\ddot{β}}_{m 1}$ , and $z_{m 1}$ - $z_{w 1}$ are treated as follows: $σ_{1} = σ_{{\ddot{z}}_{m 1}} / σ_{{\ddot{z}}_{m 1 b}}$ , $σ_{2} = σ_{{\ddot{β}}_{m 1}} / σ_{{\ddot{β}}_{m 1 b}}$ , $σ_{3} = σ_{(z_{m 1} - z_{w 1})} / σ_{(z_{m 1 b} - z_{w 1 b})}$ , where, $b$ represents the vibration responses under the original vehicle parameters. Since the similarity of the vibration laws of the four motors, only the analysis results of the first motor are given here.

As can be seen from Fig. 7, with the increase of $K_{m 1}$ and $K_{m 2}$ , $σ_{1}$ and $σ_{2}$ decrease first, then increase and finally stabilize, $σ_{3}$ decreases first and then stabilizes; with the increase of $C_{m 1}$ and $C_{m 2}$ , $σ_{1}$ and $σ_{2}$ decrease first and then increase, and $σ_{3}$ hardly changes. It can be seen that, under the condition of a given mass of the motor, there are optimal $K_{m 1}$ , $K_{m 2}$ , $C_{m 1}$ , and $C_{m 2}$ values which minimize the vertical and pitching vibration accelerations of the motor, and the values of $K_{m 1}$ and $K_{m 2}$ in a certain range of stiffness can help to reduce the relative clearance between the stator and the rotor of the motor, that is, to improve the uneven distribution of the air gap magnetic field of the motor. Among them, the sensitivity degree of $σ_{1}$ and $σ_{2}$ to each suspension parameter is in the order of $K_{m 1}$ , $K_{m 2}$ , $C_{m 1}$ , and $C_{m 2}$ .

6. Conclusions

In this paper, a vehicle-track vertical coupling dynamic model with considering the influence of the frame-mounted traction motor is established. And then, by considering both the track irregularity excitation and the traction motor vibration characteristics, the vertical vibration responses of the train with frame-mounted traction motor are simulated, and the correctness of the dynamic model established is verified by the real vehicle test. According to the results, the following conclusions can be drawn:

1) Traction motor is significantly affected by the train system, when the motor is equivalent to the bogie frame mass, the phenomenon of underestimation exists to evaluate the vibration of the motor, therefore, when analyzing the vibration characteristics of the traction motor, the coupling effect between the train system and the traction motor should be considered.

2) Suspension parameters have a great impact on the vibration responses of the traction motor. There are optimal $K_{m 1}$ , $K_{m 2}$ , $C_{m 1}$ , and $C_{m 2}$ values which minimize the vertical and pitching vibration accelerations of the motor. Rational selection of suspension parameters will help to attenuate the vibration of the traction motor, and alleviate uneven the distribution of air gap magnetic field of the traction motor. The dynamic model can be further used to optimize the stiffness and damping parameters of the traction motor suspension system.

References

Evans J., Berg M. Challenges in simulation of rail vehicle dynamics. Vehicle System Dynamics, Vol. 47, Issue 8, 2009, p. 1023-1048.

Publisher
Zhai W. M. Vehicle-Track Coupled Dynamics. Fourth Edition, Science Press, Beijing, 2015.

Search CrossRef
Dimitriu M. On the critical points of vertical vibration in a railway vehicle. Archive of Mechanical Engineering, Vol. 61, Issue 4, 2014, p. 609-625.

Publisher
Lu F., Kennedy D., Williams F. W., et al. Symplectic analysis of vertical random vibration for coupled vehicle track systems. Journal of Sound and Vibration, Vol. 317, Issues 1-2, 2008, p. 236-249.

Publisher
Nagai M., Yoshida H., Tohtake T., et al. Coupled vibration of passenger and lightweight car-body in consideration of human-body biomechanics. Vehicle System Dynamics, Vol. 44, 2006, p. 601-611.

Publisher
Wu X. W., Chi M. R., Gao H. The study of post-derailment dynamic behavior of railway vehicle based on running tests. Engineering Failure Analysis, Vol. 44, Issue 5, 2014, p. 382-399.

Publisher
Wu X. W., Chi M. R., Gao H. Post-derailment dynamic behaviour of a high-speed train under earthquake excitations. Engineering Failure Analysis, Vol. 64, 2016, p. 97-110.

Publisher
Alfi S., Mazzola L., Bruni S. Effect of motor connection on the critical speed of high-speed railway vehicles. Vehicle System Dynamics, Vol. 46, 2008, p. 201-214.

Publisher
Yao Y., Zhang K. L., Luo S. H. The mechanism of dynamic effect of the driving system elastically mounted on the bogie frame of locomotive. Journal of Vibration Engineering, Vol. 25, Issue 5, 2012, p. 481-487.

Search CrossRef
Luo Y., Jin D. C. Research on the rules of suspension parameters to driving equipments suspended in bogie frames. China Railway Science, Vol. 4, 2007, p. 78-82.

Search CrossRef
Senini F., Flinders S., Oghanna W. Dynamic Simulation of Wheel-Rail Interaction for Locomotive Traction Studies. Railroad Conference, Pittsburgh, 1993.

Search CrossRef
Zhai W. M. Locomotive-and-track system coupling dynamics and its application to the study of hoeomotwe performance. China Railway Science, Vol. 2, 1996, p. 58-73.

Search CrossRef
Zhai W. M. Study of wheel/rail dynamic performance of electric drive locomotive. Electric Drive for Locomotives, Vol. 6, 1996, p. 10-13.

Search CrossRef
Zhai W. M., Cai C. B. Effect of locomotive vibrations on pantograph-catenary system dynamics. Vehicle System Dynamics, Vol. 29, 1998, p. 47-58.

Publisher
Chen Z. G., Zhai W. M., Wang K. Y. Dynamic investigation of a locomotive with effect of gear transmissions under tractive conditions. Journal of Sound and Vibration, Vol. 408, 2017, p. 220-233.

Publisher
Chen Z. G., Zhai W. M., Wang K. Y. Vibration feature evolution of locomotive with tooth root crack propagation of gear transmission system. Mechanical Systems and Signal Processing, Vol. 115, 2019, p. 29-44.

Publisher
Liu P. F., Zhai W. M., Wang K. Y., et al. Theoretical and experimental study on vertical dynamic characteristics of six-axle heavy-haul locomotive on curve. Transport, Vol. 33, 2018, p. 291-301.

Publisher
Jin X. S., Wen Z. F., Wang K. Y., et al. Three-dimensional train–track model for study of rail corrugation. Journal of Sound and Vibration, Vol. 293, Issues 3-5, 2006, p. 830-855.

Publisher
Zhai W. M., Wang K. Y., Cai C. B. Fundamentals of vehicle-track coupled dynamics. Vehicle System Dynamics, Vol. 47, Issue 11, 2009, p. 1349-1376.

Publisher
Sowiński B. Interrelation between wavelengths of track geometry irregularities and rail vehicle dynamic properties. The Archives of Transport, Vols. 25-26, Issue 1-2, 2013, p. 97-108.

Search CrossRef
Sowiński B., Kostrzewski M. Railway vehicle transient vibration as a factor of track irregularities formation. Proceedings of the 13th Mini Conference on Vehicle System Dynamics, Identification and Anomalies, 2012.

Search CrossRef
Mao J. F., Yu Z. W., Xiao Y. J. Random dynamic analysis of a train-bridge coupled system involving random system parameters based on probability density evolution method. Probabilistic Engineering Mechanics, Vol. 46, 2016, p. 48-61.

Publisher

Cited by

Improved Dynamics Model of Locomotive Traction Motor with Elasticity of Rotor Shaft and Supporting Bearings

Yuqing Liu | Zaigang Chen | Jieyu Ning | Kaiyun Wang | Wanming Zhai

(2022)

About this article

Received

10 July 2019

Accepted

03 November 2019

Published

15 February 2020

SUBJECTS

Vibration in transportation engineering

DOI

https://doi.org/10.21595/jve.2019.20900

Keywords

train

traction motor

mounted on the bogie frame

electromechanical coupling

dynamic characteristics

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2022 08 25

Study on the influence of wheel polygon on the vibration characteristics of bogie system

Zhihui Niu, Fangchao Pang, Xinfeng Zhang, Tianqiang Du, Jian Su

Research article

2022 05 15

Dynamic characteristic analysis of a multi-power coupling transmission system considering non-torque loads

Ruizhi Shu, Jinghua Ma, Jin Huang, Shuaishuai Ge, Benyuan Fu, Rulong Tan, Zheng Zou

Research article

2019 03 31

Study on an elastic lever system for electromagnetic energy harvesting from rail vibration

Ping Wang, Fan Yang, Mingyuan Gao, Yuan Wang

Research article

2017 06 30

Vibration signal analysis and fault diagnosis of bogies of the high-speed train based on deep neural networks

Yang Zhao, Zheng Hong Guo, Jian Ming Yan

Y. Yu, L. Zhao, and C. Zhou, “Effect of vehicle-track vertical coupling vibrations on frame-mounted traction motor dynamics,” Journal of Vibroengineering, Vol. 22, No. 1, pp. 184–196, Feb. 2020, https://doi.org/10.21595/jve.2019.20900

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2019.20900
UR  - https://doi.org/10.21595/jve.2019.20900
TI  - Effect of vehicle-track vertical coupling vibrations on frame-mounted traction motor dynamics
T2  - Journal of Vibroengineering
AU  - Zhou, Changcheng
AU  - Yu, Yuewei
AU  - Zhao, Leilei
PY  - 2020
DA  - 2020/02/15
PB  - JVE International Ltd.
SP  - 184-196
IS  - 1
VL  - 22
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

@article{Zhou_2020,
	doi = {10.21595/jve.2019.20900},
	url = {https://doi.org/10.21595/jve.2019.20900},
	year = 2020,
	month = {feb},
	publisher = {{JVE} International Ltd.},
	volume = {22},
	number = {1},
	pages = {184--196},
	author = {Changcheng Zhou and Yuewei Yu and Leilei Zhao},
	title = {Effect of vehicle-track vertical coupling vibrations on frame-mounted traction motor dynamics},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]C. Zhou, Y. Yu, and L. Zhao, “Effect of vehicle-track vertical coupling vibrations on frame-mounted traction motor dynamics,” Journal of Vibroengineering, vol. 22, no. 1, pp. 184–196, Feb. 2020, doi: 10.21595/jve.2019.20900.

Copy IEEE

Copied to clipboard!

Zhou, Changcheng, Yuewei Yu, and Leilei Zhao. “Effect of Vehicle-Track Vertical Coupling Vibrations on Frame-Mounted Traction Motor Dynamics.” Journal of Vibroengineering 22, no. 1 (February 15, 2020): 184–96. https://doi.org/10.21595/jve.2019.20900.

Copy Chicago

Copied to clipboard!

Effect of vehicle-track vertical coupling vibrations on frame-mounted traction motor dynamics

Abstract

Highlights

1. Introduction

2. Vehicle-track vertical coupling dynamic model with considering the frame-mounted traction motor

2.1. Physical model of the vertical coupling system

2.2. Mathematical model of the vertical coupling system

2.3. Numerical solution of the system dynamic response

3. Test verification of the vertical coupling dynamic model

4. The influence of the vehicle-track vertical coupling vibrations on the frame-mounted traction motor dynamics

4.1. Influence of train system on the vibration response of the traction motor

4.2. Influence of electromechanical coupling on the vibration response of the traction motor

5. The influence of the suspension parameters on the frame-mounted traction motor dynamics

6. Conclusions

References

Cited by

About this article

Related Articles