Effect of annulus drilling fluid on lateral vibration of drillstring

Yang, Chunxu; Wang, Rui-He; Han, Laiju; Xue, Qilong; Li, Lixin

doi:10.21595/jve.2019.20473

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 February 2020

Check for updates

Effect of annulus drilling fluid on lateral vibration of drillstring

Chunxu Yang¹

Rui-He Wang²

Laiju Han³

Qilong Xue⁴

Lixin Li⁵

^{1, 2}Petroleum Engineering College of China University of Petroleum, Qingdao, P. R. China

^{3, 1}Shengli Petroleum Engineering Co. Ltd, Drilling Technology Research Institute, Dongying, P. R. China

⁴School of Engineering and Technology, China University of Geosciences, Beijing, P. R. China

⁵Chinese Academy of Geological Sciences, Beijing, P. R. China

Corresponding Author:

Lixin Li

Cite the article Download PDF

Downloads 1348

WoS Core Citations 2

CrossRef Citations 2

Abstract

Annular drilling fluid between the drillstring and borehole wall has a great influence on lateral vibration of drillstring and the influence involves the added mass. Assuming the drilling fluid is incompressible, we derive the added mass coefficient that annular drilling fluid influences on lateral vibration of drillstring in the case of axial flow of drilling fluid. When the axial flow of drilling fluid is considered, the added mass coefficient is difficult to solve. We apply CFD method and dynamic mesh technique to establish the calculation model for the flow in the annulus caused by the vibration of drillstring in the annulus. The pressure distribution and velocity distribution of annular drilling fluid are obtained. The added mass force of the drilling fluid acting on the drillstring along the direction of the drillstring is obtained from the pressure distribution, and the added mass coefficient of the lateral vibration of the drillstring is obtained. This paper provides the basis to solve the added mass coefficient of the lateral vibration of drillstring considering axial flow of drilling fluid.

Highlights

The added mass coefficient of the annular drilling fluid’s influence on the lateral vibration of the drillstring is derived
Using CFD method and dynamic mesh technology to simulate the annular flow caused by the vibration of drillstring in the annular drilling fluid under two-dimensional conditions
Providing the basis to solve the added mass coefficient that drillstring of lateral vibration under consideration of axial flow

1. Introduction

It has been proved that drilling dynamics and its interactions with the surroundings are the essential reason of a lot of dangerous drilling accidents, such as the poor cementing quality induced by the deterioration of borehole quality and the failure of drilling tools caused by strong vibration [1, 2]. As the most common dynamics phenomenon, severe vibrations of drillstring must be paid enough attention. The drillstring is consisted of several drill pipes, drill collars, stabilizers and connections, both are under heavy dynamic loads with extreme complexity. If the excited frequency of drillstring closes to the natural frequencies of its components, the energy will be absorbed. Once the resonance appears and the energy boosts, the amplitude of drillstring vibration will be increased, and the bending of drillstring will be intensified, by which the early fatigue of tools will occur [3], and the tools life will be reduced significantly. There are three typical modes of drillstring vibration, namely are the longitudinal vibration (also called axial vibration) mode, the transverse (also referred to lateral or bending) mode and the torsional (also known as stick-slip) mode. The destructive nature of each type of vibration is different, it is well known that lateral vibration [4] is the main reason for drillstring failure as the study of drillstring dynamics goes further. Many dangerous phenomena related to drilling are normally caused by the dynamics of the drillstring and its interactions with the surroundings.

The destructive nature of each type of vibration is different, among them, the longitudinal vibration owns the most intuitionistic destructive behavior and action. The axial vibration of the drillstring can be defined using discrete mass segments and springs [5] and the frequency response function can be used to demonstrate the similarity of the model to the real drillstring response. Aadnoy et al. [6] studies using the static model of the drillstring and the rotation of the drillstring to reduce the drillstring borehole friction during torsional vibration. Wolf S. F. et al. [7] measured down hole parameters like bottom force and acceleration during vertical drilling, and it was found that resonant frequency of the system is lower than intrinsic frequency of drillstring [8]. The bending moment obtained by static simulation is one order of magnitude smaller than the real one, and a high bending moment was observed at the bottom which cannot be surveyed at the wellhead [9]. Qilong X. et. al. [10-11] studied the effect of annulus drilling fluid damping on drillstring lateral vibration, and it was found that the additional quality caused by drilling fluid is at the same order of magnitude of the quality of drillstring, which cannot be neglected. Some studies are dedicated to better understanding the full dynamics of rotary drilling systems [12-14]. Sunit [15] develops the global dynamics of coupled axial torsional vibration and the possibility of bit bounce. Brebbia [16] used the boundary element method of solid mechanics to calculate velocity potential in fluid flow, which makes the calculation method simpler. Sarpkaya [17, 18] studied the added mass of cylindrical vortex-induced oscillation (VIO) through experiments. It was found that the added mass varied greatly with the ratio of amplitude to diameter, and the added mass was negative at some time. Villaggio [19] calculated the added mass of an infinite cylinder with elastic deformation, but the elastic vibration was not considered in the calculation process. Heisig G. et al. [20] studied the impact between drillstring and borehole wall and deduced the lateral vibration model of drillstring.

During the downward movement of the drillstring, the lateral vibration of the drillstring is the most complex movement of the drillstring vibration, and the drilling fluid in the drillstring and the borehole annulus is the main factor causing the lateral vibration of the drillstring. Lateral vibration is mainly caused by drillstring deformation which is caused by fluid-solid coupling and interrelation between drilling fluid and drillstring. Added mass is usually involved in solving fluid-solid coupling systems. None of works has obtained added mass coefficients in the case of axial motion. This paper mainly analyses the mass effect of annular drilling fluid on drillstring lateral resonance and calculates added mass coefficients by potential flow theory under the condition of axial motion, which provides a reference for engineering application of drilling process.

2. Methods and models

2.1. Basic assumptions

Assuming the diameter of the drillstring is $d$ , the diameter of the borehole wall is $D$ , and the axial direction of the drillstring is the $Z$ direction, as shown in Fig. 1. If the lateral movement of the drillstring is a harmonic motion in the Y direction, the displacement of the drillstring can be expressed by the following formula:

1

y = y (z) e^{i ω t},

where $y (z)$ is the amplitude of the drillstring vibration, $ω$ is the frequency of the drillstring vibration, and $t$ is the time, $i = \sqrt{- 1}$ .

Assuming that the fluid is homogeneous and incompressible, the sound velocity in the drilling fluid is considered to be very fast, and ignoring the influence of the vibration frequency of the drillstring, there is a velocity potential function $φ (r, z, θ, t) = ψ (r, θ, z) e^{i ω t}$ and the following formula is satisfied:

2

\nabla^{2} ψ = \frac{\partial^{2} ψ}{\partial r^{2}} + \frac{\partial ψ}{r \partial r} + \frac{\partial^{2} ψ}{r^{2} \partial θ^{2}} + \frac{\partial^{2} ψ}{\partial z^{2}} = 0 .

In the formula, $\nabla^{2}$ is a Laplacian operator, $φ$ is a potential function of velocity and $ψ$ is an amplitude function.

2.2. Derivation of added mass coefficient

Density and pressure at any point in drilling fluid can be expressed as:

3

\{\begin{array}{l} ρ = ρ_{0} + ρ_{e}, (ρ_{0} ≫ ρ_{e}), \\ p = p_{0} + p_{e}, (p_{0} ≫ p_{e}) . \end{array}

Subscripts 0 and $e$ represent the mean and fluctuation values, respectively, and assuming the fluctuation of the pressure is a harmonic function of time and satisfies the wave equation, the pressure and velocity at any point in the drilling fluid can be expressed by the following equations:

4

\{\begin{array}{l} v_{r} = \frac{\partial ϕ}{\partial r}, v_{θ} = \frac{\partial ϕ}{r \partial θ}, v_{z} = \frac{\partial ϕ}{\partial z}, \\ p_{e} = ρ \frac{\partial ϕ}{\partial t} . \end{array}

Fig. 1Schematic diagram of the movement of the drillstring in the annulus of drilling fluid

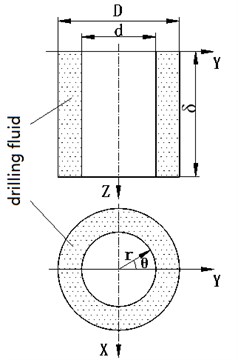
The boundary conditions of the drilling fluid can be expressed as:

5

\{\begin{array}{l} v_{r} |_{r = \frac{D}{2}} = 0, \\ v_{r} |_{r = \frac{d}{2}} = c o s θ \frac{\partial y}{\partial t} . \end{array}

Using the method of separation of variables, $ψ (r, θ, z)$ can be expressed as the following form:

6

ψ (r, θ, z) = R (r) Θ (θ) Z (z) .

The following formula can be obtained by substituting Eq. (6) into Eq. (2):

7

\frac{d^{2} R}{d r^{2}} Θ Z + \frac{d R}{r d r} Θ Z + \frac{d^{2} Θ}{r^{2} d θ^{2}} R Z + \frac{d^{2} Z}{d z^{2}} R Θ = 0,

8

\frac{d^{2} R}{R d r^{2}} + \frac{1}{r R} \frac{d R}{d r} - \frac{m^{2}}{r^{2}} = - \frac{1}{Z} \frac{d^{2} Z}{d z^{2}} = - μ .

(1) When $x =$ 0, by solving the differential equation the following formulas can be obtained:

9

\{\begin{array}{l} Θ (θ) = A_{1} s i n (m θ) + A_{2} c o s (m θ), m = 1,2, \dots, \\ Z (z) = B_{1} + B_{2} z, \\ R (r) = C_{1} r^{m} + C_{2} r^{- m} . \end{array}

Velocity potential function can be obtained from Eqs. (6)-(9):

10

φ = [A_{1} s i n (m θ) + A_{2} c o s (m θ)] [B_{1} + B_{2} z] [C_{1} r^{m} + C_{2} r^{- m}] e^{i ω t} .

By using the boundary condition Eq. (5) and substituting Eq. (10) into Eq. (4), the solution is obtained:

11

\{\begin{array}{l} y (z) = Z (z) = B_{1} + B_{2} z, \\ φ (r, θ, z, t) = i ω (B_{1} + B_{2} z) \frac{d^{2}}{d^{2} - D^{2}} (r + \frac{D^{2}}{4 r}) c o s θ e^{i ω t}, \\ p_{e} = - ω^{2} ρ (B_{1} + B_{2} z) \frac{d^{2}}{d^{2} - D^{2}} (r + \frac{D^{2}}{4 r}) c o s θ e^{i ω t} . \end{array}

In the formula, $B_{1}$ , $B_{2}$ are the coefficients of linear vibration of drillstring along the axial direction when $μ = 0$ .

According to the pressure $p_{e}$ of drilling fluid, the added mass force acting on the drillstring along the direction of drillstring movement can be calculated:

12

P_{f} = - \int_{0}^{δ} \int_{0}^{2 π} \frac{d}{2} (p_{o} + p_{e}) |_{r = \frac{d}{2}} c o s θ d θ d z = - \frac{π d^{2}}{4} ω^{2} ρ \frac{D^{2} + d^{2}}{D^{2} - d^{2}} e^{i ω t} (B_{1} δ + \frac{1}{2} B_{2} δ^{2}) .

By introducing the concept of added mass force, there are:

13

m_{f} \frac{\partial^{2} y}{\partial t^{2}} = P_{f} = \frac{π d^{2}}{4} δ ρ C_{M} \frac{\partial^{2} y}{\partial t^{2}} = - \frac{π d^{2}}{4} ω^{2} ρ \frac{D^{2} + d^{2}}{D^{2} - d^{2}} e^{i ω t} (B_{1} δ + \frac{1}{2} B_{2} δ^{2}) .

Solving the equation above, $C_{M}$ is written as:

14

C_{M} = \frac{D^{2} + d^{2}}{D^{2} - d^{2}} \cdot \frac{2 B_{1} + B_{2} δ}{2 (B_{1} + B_{2} z)} .

(2) When $μ > 0$ , by solving the differential equation the following formulas can be obtained:

15

\{\begin{array}{l} Θ (θ) = A_{1} s i n (m θ) + A_{2} c o s (m θ), m = 1,2, \dots, \\ Z (z) = B_{1} e^{\sqrt{μ} z} + B_{2} e^{- \sqrt{μ} z}, \\ R (r) = C_{1} J_{m} (\sqrt{μ} r) + C_{2} Y_{m} (\sqrt{μ} r) . \end{array}

In the formula, $J_{m} (\sqrt{μ} r)$ is the $m$ -Bessel function of the first kind and $Y_{m} (\sqrt{μ} r)$ is the $n$ -Bessel function of the second kind.

Substituting velocity potential function into Eqs. (4) and (5), the following formulas are obtained:

16

\{\begin{array}{l} y (z) = Z (z) = B_{1} e^{\sqrt{μ} z} + B_{2} e^{- \sqrt{μ} z}, \\ φ (r, θ, z, t) = i ω (B_{1} e^{\sqrt{μ} z} + B_{2} e^{- \sqrt{μ} z}) H (\sqrt{μ} r) c o s θ e^{i ω t}, \\ p_{e} = - ω^{2} ρ (B_{1} e^{\sqrt{μ} z} + B_{2} e^{- \sqrt{μ} z}) H (\sqrt{μ} r) c o s θ e^{i ω t}, \\ H (\sqrt{μ} r) = \frac{Y_{1}^{'} (\sqrt{μ} \frac{D}{2}) J_{1} (\sqrt{μ} r) - J_{1}^{'} (\sqrt{μ} \frac{D}{2}) Y_{1} (\sqrt{μ} r)}{J_{1}^{'} (\sqrt{μ} \frac{d}{2}) Y_{1}^{'} (\sqrt{μ} \frac{D}{2}) - J_{1}^{'} (\sqrt{μ} \frac{D}{2}) Y_{1}^{'} (\sqrt{μ} \frac{d}{2})} . \end{array}

In the formula, $B_{1}$ and $B_{2}$ the coefficients of axial vibration of drillstring when $u =$ 0.

Similarly, the following formula is obtained:

17

C_{M} = H (\sqrt{μ} \frac{d}{2}) \frac{B_{1} - B_{2} - B_{1} e^{\sqrt{μ} δ} + B_{2} e^{- \sqrt{μ} δ}}{\sqrt{μ} δ (B_{1} e^{\sqrt{μ} z} + B_{2} e^{- \sqrt{μ} z})} \cdot \frac{2}{d} .

(3) When $μ < 0$ , the following equation is obtained by solving the equation:

18

\{\begin{array}{l} Θ (θ) = A_{1} s i n (m θ) + A_{2} c o s (m θ), m = 1,2, \dots, \\ Z (z) = B_{1} s i n (\sqrt{- μ} z) + B_{2} c o s (\sqrt{- μ} z), \\ R (r) = C_{1} I_{m} (\sqrt{- μ} r) + C_{2} K_{m} (\sqrt{- μ} r) . \end{array}

In the formula, $I_{m} (\sqrt{μ} r)$ is $m$ -order virtual scalar Bessel function, $K_{m} (\sqrt{μ} r)$ is $m$ -order virtual scalar Hankel function.

According to the boundary conditions, the following solution is obtained:

19

\{\begin{array}{l} y (z) = Z (z) = B_{1} s i n (\sqrt{- μ} z) + B_{2} c o s (\sqrt{- μ} z), \\ φ (r, θ, z, t) = i ω [B_{1} s i n (\sqrt{- μ} z) + B_{2} c o s (\sqrt{- μ} z)] H (\sqrt{- μ} r) c o s θ e^{i ω t}, \\ p_{e} = - ω^{2} ρ [B_{1} s i n (\sqrt{- μ} z) + B_{2} c o s (\sqrt{- μ} z)] H (\sqrt{- μ} r) c o s θ e^{i ω t}, \\ H (\sqrt{- μ} r) = \frac{K_{1}^{'} (\sqrt{- μ} \frac{D}{2}) I_{1} (\sqrt{- μ} r) - I_{1}^{'} (\sqrt{- μ} \frac{D}{2}) K_{1} (\sqrt{- μ} r)}{I_{1}^{'} (\sqrt{- μ} \frac{d}{2}) K_{1}^{'} (\sqrt{- μ} \frac{D}{2}) - I_{1}^{'} (\sqrt{- μ} \frac{D}{2}) K_{1}^{'} (\sqrt{- μ} \frac{d}{2})} . \end{array}

In the formula, $B_{1}$ and $B_{2}$ are the coefficients of axial vibration of drillstring when $u <$ 0:

20

C_{M} = H (\sqrt{- μ} \frac{d}{2}) \frac{B_{1} c o s \sqrt{- μ} δ - B_{2} s i n \sqrt{- μ} δ - B_{1}}{\sqrt{- μ} δ [B_{1} \sin (\sqrt{- μ} z) + B_{2} \cos (\sqrt{- μ} z)]} \cdot \frac{2}{d} .

From the above Eqs. (14), (17), (20), it can be seen that after considering the axial flow of drilling fluid, the added mass coefficient $C_{M}$ is related to the axial motion $y (z)$ , but the solution is difficult to obtain. We can consider using CFD method and dynamic mesh technology to establish the calculation model of drill string’s lateral vibration in annular drilling fluid, and then we can get pressure distribution and velocity distribution in drilling fluid. According to the pressure distribution and velocity distribution, the added mass force of drilling fluid along the direction of drillstring motion acting on drillstring is calculated, and the added mass coefficient of drillstring lateral vibration is obtained.

3. Results and discussion

When CFD method and dynamic mesh technology are used to solve the added mass coefficient $C_{M}$ , the calculation model of drillstring lateral vibration in annular drilling fluid is established firstly, and the added mass force acting on drillstring is calculated by pressure distribution, thus the added mass coefficient of drillstring lateral vibration is obtained. In modeling, we can build a two-dimensional model. Without considering the axial flow, the added mass coefficient can be obtained by numerical simulation. Then, the method is compared with the added mass coefficient (approximately 2.7) calculated by the known theoretical formula [18]. If the error between the two methods is small, the feasibility of the method is proved.

3.1. Geometric modeling and mesh generation

The two-dimensional geometric model of drillstring in annular drilling fluid is shown in Fig. 2(a). The inner circle is drillstring, diameter $d =$ 127 mm, the outer circle is shaft wall, diameter $D =$ 187 mm and the annulus fills with drilling fluid, density $ρ =$ 1150 kg/m³. Since the model is simple, there is no need to simplify it, we can directly generate the grid. We use the dynamic mesh technology, which generally uses the triangular mesh. The divided meshes are shown in Fig. 2(b).

Fig. 2Computing model and meshes

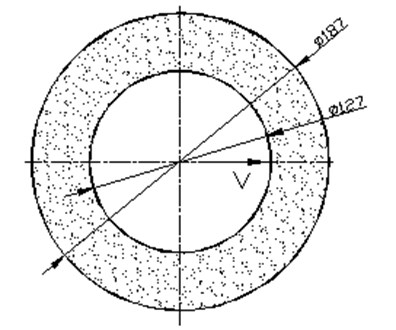
a) Geometric model

b) Divided meshes

3.2. Physical model

Under the incompressible assumption, a standard $k$ - $ε$ turbulence model is selected for numerical simulation based on the turbulence governing equations. K-epsilon ( $k$ - $ε$ ) turbulence model is the most common model used in Computational Fluid Dynamics (CFD) to simulate mean flow characteristics for turbulent flow conditions. It is a two-equation model that gives a general description of turbulence by means of two transport equations (PDEs). The original impetus for the K-epsilon model was to improve the mixing-length model, as well as to find an alternative to algebraically prescribing turbulent length scales in moderate to high complexity flows.[21]

The $k$ - $ε$ turbulence model is a semi-empirical and semi-theoretical formula, and $k$ and $ε$ are determined by the following equations:

21

\frac{\partial}{\partial t} (ρ k) + \frac{\partial}{\partial x_{i}} (ρ k u_{i}) = \frac{\partial}{\partial x_{j}} [(μ + \frac{μ_{t}}{σ_{k}}) \frac{\partial k}{\partial x_{j}}] + G_{k} + G_{b} - ρ ε - Y_{M} + S_{k},

22

\frac{\partial}{\partial t} (ρ ε) + \frac{\partial}{\partial x_{i}} (ρ ε u_{i}) = \frac{\partial}{\partial x_{j}} [(μ + \frac{μ_{t}}{σ_{ε}}) \frac{\partial ε}{\partial x_{j}}] + C_{1 ε} \frac{ε}{k} (G_{k} + C_{3 ε} G_{b}) - C_{2 ε} ρ \frac{ε^{2}}{k} + S_{ε} .

Among them, $G_{k}$ is the turbulent kinetic energy term caused by the average velocity gradient. Its formula is written as:

23

G_{k} = μ_{t} (\frac{\partial u_{i}}{\partial μ_{j}} + \frac{\partial u_{j}}{\partial x_{i}}) \frac{\partial u_{i}}{\partial x_{j}} .

In the formula, $μ_{t}$ is the turbulent viscosity, $μ_{t} = ρ C_{μ} \frac{k^{2}}{ε}$ and $C_{μ}$ is the empirical constant.

$G_{b}$ in Eq. (21) and Eq. (22) is a term of turbulent kinetic energy generated by buoyancy, and its formula is as follows:

24

G_{b} = β g_{i} \frac{μ_{t}}{P r_{l}} \frac{\partial T}{\partial x_{i}} .

Among them, $β$ is the coefficient of thermal expansion, $β = - \frac{1}{ρ} \frac{\partial ρ}{\partial t}$ ; $P r_{l}$ is the Plandtl number of energy turbulence, $P r_{l} =$ 0.85.

In Eq. (21), Y_M indicates the impact of turbulent fluctuating expansion on dissipative energy in compressible fluid. The formula is as follows:

25

Y_{M} = 2 ρ ε M_{t}^{2} .

Among them, $M_{t}$ is the Mach number of turbulence, $M_{t} = \sqrt{k / a^{2}}$ ; $a$ is the sound velocity, $a = \sqrt{γ R T}$ .

For compressible flow, $G_{b} =$ 0, $Y_{M} =$ 0.

$σ_{k}$ and $σ_{ε}$ in Eq. (21) and Eq. (22) are turbulent Prandtl numbers corresponding to turbulent kinetic energy and dissipation rate; $C_{1 ε}$ , $C_{2 ε}$ , $C_{3 ε}$ are empirical constants, and $S_{k}$ , $S_{ε}$ are self-defined source terms, which can be ignored when the external energy does not exist.

According to the recommended values and experimental verification, the constant values of the model are respectively $C_{1 ε} =$ 1.44, $C_{2 ε} =$ 1.92, $C_{μ} =$ 0.09, $σ_{k} =$ 1.0, $σ_{ε} =$ 1.3.

3.3. Boundary condition setting

The boundary conditions of the calculation model of drillstring lateral vibration influenced by annular drilling fluid are set as follows. The annular part is set as a deformable fluid area and the drillstring motion equation is $x = A s i n (θ t)$ . In the formula, $A$ is the amplitude and $θ$ is the angular frequency. The vibration velocity of drillstring is imported into FLUENT by UDF programming. The standard $k$ - $ε$ turbulence model is selected to simulate the unsteady transient flow, and the grid is set as a moving grid. By changing the parameters of the motion equation, the motion of three different cases was simulated. The cases are amplitude 5 mm and frequency 1.5 Hz, amplitude 10 mm and frequency 2 Hz, amplitude 15 mm and frequency 1.5 Hz, respectively.

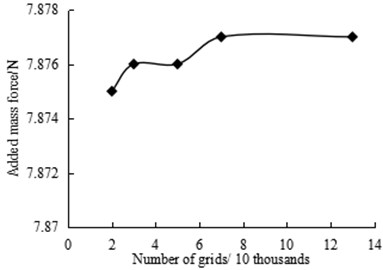
Fig. 3Added mass force for different grid numbers at 1.25 s

3.4. Verification of grid independence

In order to verify the independence of the grid, on condition that the amplitude is 5 mm and the frequency is 1 Hz, the simulation of 20000, 30000, 50000, 70000 and 130000 grids is carried out respectively. Fig. 3 shows the added mass force for different grid numbers at 1.25 s.

As can be seen from Fig. 3, when the number of grids changes from 20 thousands to 130 thousands, the value of added mass force changes little with the increase of the number of grids. It can be considered that when the number of grids is 70000, the simulation result is independent of the grid, so 70000 grids are taken as the calculation grid.

3.5. Analysis of calculation results

After calculation, when amplitude is 5 mm, frequency is 1 Hz, the pressure contours and velocity vector plots at 1.18 s, 1.25 s, 1.32 s and 1.37 s are shown in Fig. 4 and Fig. 5.

Fig. 4Pressure distribution contour at different time

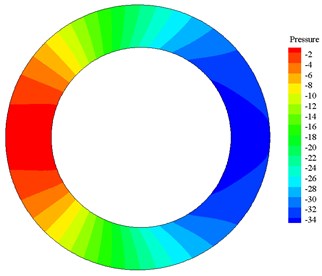
a) Pressure distribution at 1.18 s

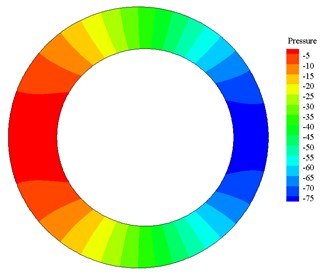
b) Pressure distribution at 1.25 s

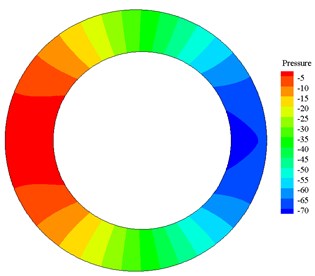
c) Pressure distribution at 1.32 s

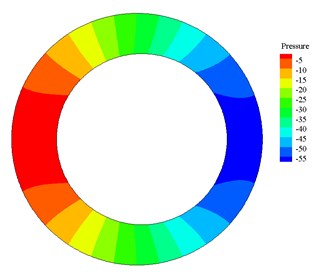
d) Pressure distribution at 1.37 s

Pressure distribution contours in Fig. 4 and velocity vector plots in Fig. 5 correspond to each other. In Fig. 4 and Fig. 5, from (a) to (b) the high-pressure area on the left side becomes wider, the pressure increases, the velocity decreases and is positive (the right is positive direction). According to the motion equation, the acceleration is negative, and the magnitude of acceleration increases continuously, so from (a) to (b) drillstring decelerates to the right. When motion time of drillstring reaches 1.25 s, the pressure reaches the maximum, the acceleration reaches the maximum and the velocity is 0. From (b) to (c) and then to (d), the high-pressure zone on the left side narrows, the pressure decreases, the velocity increases and is negative (the left is in negative direction). According to the equation of motion, the acceleration is negative and the acceleration decreases, so the drillstring accelerates to the left. It shows that the pressure produced by the flow impedes the movement of the drillstring, which is the added mass effect.

By reading out the force on the drillstring, the added mass coefficient can be obtained as shown in tables 1, 2 and 3. As can be seen from Tables 1, 2 and 3, the added mass coefficient of drillstring lateral vibration is independent of amplitude and frequency, and the error between the simulation results and theoretical calculation results is small, which meets the needs of engineering calculation.

Fig. 5Velocity vector plot at different time

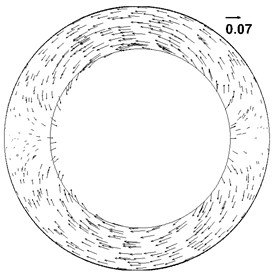
a) Velocity vector plot at 1.18 s

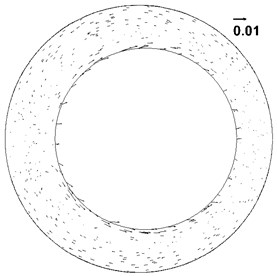
b) Velocity vector plot at 1.25 s

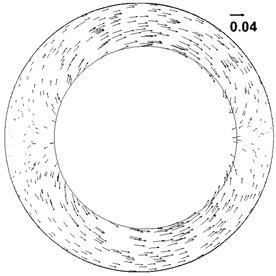
c) Velocity vector plot at 1.32 s

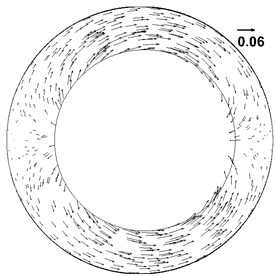
d) Velocity vector plot at 1.37 s

Table 1Added mass coefficient calculation results in case of amplitude 5mm, frequency 1 Hz

Time / s	Added mass force / N	Added mass force coefficient	Error
1.18	–7.00	2.69	0.78 %
1.25	–7.877	2.74	0.98 %
1.32	–7.204	2.77	2.04 %
1.37	–5.860	2.80	2.98 %

Table 2Added mass coefficient calculation results in case of amplitude 15 mm, frequency 1.5 Hz

Time / s	Added mass force / N	Added mass force coefficient	Error
0.084	36.246	2.62	3.34 %
1.111	46.638	2.78	2.30 %
1.223	47.999	2.87	5.42 %
1.25	38.248	2.79	2.67 %

Table 3Added mass coefficient calculation results in case of amplitude 10 mm, frequency 2 Hz

Time / s	Added mass force / N	Added mass force coefficient	Error
0.565	–43.349	2.59	4.92 %
0.625	–65.009	2.83	4.02 %
0.815	43.522	2.60	4.50 %
0.875	65.06	2.83	4.10 %

3.6. Relevant verification of internal liquid influence on lateral vibration

Under the condition that only pipe interior is filled with drill fluid, we use the hammer strike experiments ware conducted of pipe outer diameter of 20 mm, 27 mm and 29 mm, the pipe instinct frequency was obtained. The interior mass additional coefficient of each outer diameter was computed, and instinct frequency was calculated through simulation taking its mass effect into consideration. Experimental measurement and simulation results are shown in Table 4.

As can be seen in Table 4, as the external diameter increases, the frequency increases. The simulation results are in good agreement with the test results, and the error is within 2%. Therefore, this method correctness has not been verified. We using CFD method and dynamic mesh technology, the pressure distribution and velocity distribution of annular drilling fluid are obtained, and the added mass force of drilling fluid acting on drillstring along the direction of drillstring motion is calculated from the pressure distribution, thus the added mass coefficient of drillstring lateral vibration is obtained.

Table 41st order natural frequency of drillstring when the interior is full of liquid

Outer diameter	Simulation frequency (Hz)	Experimental frequency (Hz)	Relative error	Internal additive mass coefficient
20 mm	46.42	45.52	1.98 %	0.23
27 mm	63.43	62.62	1.30 %	0.20
29 mm	68.60	69.35	1.08 %	0.22

4. Conclusions

1) Based on the assumption of incompressible fluid, in the case of drilling fluid axial flow, the added mass coefficient of the annular drilling fluid’s influence on the lateral vibration of the drillstring is derived in this paper.

2) Considering the difficulty of calculating the added mass factor in case of the axial flow of drilling fluid, we use CFD method and dynamic mesh technology to simulate the annular flow caused by the vibration of drillstring in the annular drilling fluid under two-dimensional conditions. The added mass coefficient of drillstring lateral vibration is obtained. The error between the simulation results and theoretical calculation results is small, which meets the needs of engineering calculation.

3) According to the pressure and velocity distribution of annular drilling fluid obtained by simulation, when the pressure reaches the maximum, the velocity decreases to 0, and the drillstring decelerates to the right; when the pressure decreases, the velocity increases and the drillstring accelerates to the left. Fluid pressure creates added mass effect on drillstring.

References

Ritto T. G., Escalante M. R., Sampaio R., Rosales M. B. Drill-string horizontal dynamics with uncertainty on the frictional force. Journal of Sound and Vibration, Vol. 332, Issue 1, 2013, p. 145-153.

Publisher
Xue Qilong, Leung Henry, Huang Leilei, et al. Modeling of torsional oscillation of drillstring dynamics. Nonlinear Dynamics, Vol. 96, Issues 1, 2019, p. 267-283.

Publisher
Ren Fushen, Wang Baojin, Chen Suli, Yao Zhigang, Bai Baojun Nonlinear model and qualitative analysis for coupled axial/torsional vibrations of drill string. Shock and Vibration, Vol. 2016, 2016, p. 1646814.

Publisher
Mitchell R. F., Allen M. B. Lateral vibration: the key to BHA failure analysis. World Oil, Vol. 200, Issue 4, 1985, p. 101-106.

Search CrossRef
Elsayed M. A., Phung C. C. Modeling of drillstrings. Proceedings of the 24th ASME International Conference on Offshore Mechanics and Arctic Engineering, Halkidiki, Greece, 2005.

Publisher
Aadnoy B. S., Fazaelizadeh M., Hareland G. A 3D analytical model for wellbore friction. Journal of Canadian Petroleum Technology, Vol. 49, Issue 10, 2010, p. 25-36.

Publisher
Wolf S. F., Zacksenhouse M., Arian A. Field measurements of downhole drillstring vibrations. SPE Annual Technical Conference and Exhibition, Society of Petroleum Engineers, Nevada, 1985, p. 22-26.

Publisher
Alley S. D., Sutherland G. B. The use of real-time downhole shock measurements to improve BHA component reliability. SPE Annual Technical Conference and Exhibition, Dallas, Texas, 1991.

Publisher
Batchelor G. K. An Introduction to Fluid Dynamics. Cambridge University Press, Cambridge, 1967.

Search CrossRef
Xue Qilong, Wang Ruihe, Sun Feng, Huang Zhiyuan Chaotic vibration analysis of the bottom rotating drillstring. Shock and Vibration, Vol. 2014, 2014, p. 429164.

Publisher
Xue Qilong, Henry L., Wang Ruihe, Liu Baolin, Huang Leilei, Guo Shenglai The chaotic dynamics of drilling. Nonlinear Dynamics, Vol. 3, Issue 83, 2016, p. 2003-2018.

Publisher
Khulief Y. A., Al Naser H. Finite element dynamic analysis of drillstrings. Finite Elements in Analysis and Design, Vol. 41, Issue 13, 2005, p. 1270-1288.

Publisher
Sampaio R., Piovan M. T., VeneroLozano G. Coupled axial/torsional vibrations of drill-strings by means of non-linear model. Mechanics Research Communications, Vol. 34, Issue 5, 2007, p. 497-502.

Publisher
Kapitaniak M., Hamaneh V. V., Chávez J. P., et al. Unveiling complexity of drill-string vibrations: Experiments and modelling. International Journal of Mechanical Sciences, Vols. 101-102, 2015, p. 324-337.

Publisher
Sunit K., Gupta N., Pankaj Wahi Global axial-torsional dynamics during rotary drilling. Journal of Sound and Vibration, Vol. 375, Issue 4, 2016, p. 332-352.

Publisher
Brebbia C. A., Wrobel L. C. Boundary element method for fluid flow. Advances in Water Resources, Vol. 2, 1979, p. 83-89.

Publisher
Sarpkaya T. Vortex-induced oscillations: a selective review. Journal of Applied Mechanics, Vol. 46, Issue 2, 1979, p. 241.

Publisher
Sarpkaya T. A critical review of the intrinsic nature of vortex-induced vibrations. Journal of Fluids and Structures, Vol. 19, Issue 4, 2004, p. 389-447.

Publisher
Piero Villaggio The added mass of a deformable cylinder moving in a liquid. Continuum Mechanics and Thermodynamics, Vol. 8, Issue 2, 1996, p. 115-120.

Publisher
Heisig G., Neubert M. Lateral drillstring vibrations in extended-reach wells. IADC/SPE Drilling Conference, New Orleans, Louisiana, 2000.

Publisher
Larsson I. A. S., Lindmark E. M., Lundström T. S., Nathan J. G. Secondary flow in semi circular ducts. Journal of Fluids Engineering, Vol. 133, 2011, p. 101206-101214.

Publisher

Cited by

Influence of non-Newton rheological parameters of drilling fluid on axial-lateral-torsional coupling vibration of rotating drill string

Jun Liu | Yili Chen | Shuang Liang | Mengqi Cai | Yasin Md

(2024)

Effect of Annular Gas‐Liquid Two‐Phase Flow on Dynamic Characteristics of Drill String

Baojin Wang | Zhongyang Wang | Liuci Wang | Pengyu Sun | Junhong Park

(2021)

About this article

Received

25 December 2018

Accepted

14 July 2019

Published

15 February 2020

SUBJECTS

Flow induced structural vibrations

DOI

https://doi.org/10.21595/jve.2019.20473

Keywords

annular drilling fluid

lateral vibration

drillstring

added mass coefficient

CFD

Acknowledgements

This study was funded by Natural Science Foundation of China (51704264), National Project “R&D of Key Tools and Equipment for Accelerating Drilling Speed and Efficiency in Complex Formations” (No. 2016ZX05021-003).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 03 13

Vibration-collision mechanism of dual-stabilizer bottom hole assembly system in vertical wellbore trajectory

Pan Fang, Kang Yang, Gao Li, Qunfang Feng, Shujie Ding

Research article

2020 03 31

Dynamic analysis of the longitudinal vibration on bottom drilling tools

Chunxu Yang, Rui He Wang, Laiju Han, Qilong Xue

Research article

2018 11 15

Dynamic stability of lateral vibration of a tubing string in flowing production

Song Tang, Zheng Liang, Guang Hui Zhao

Research article

2017 12 01

Transient vibration analysis of BTA deep-hole drilling shaft system

Guohong Ma, Xingquan Shen

C. Yang, R.-H. Wang, L. Han, Q. Xue, and L. Li, “Effect of annulus drilling fluid on lateral vibration of drillstring,” Journal of Vibroengineering, Vol. 22, No. 1, pp. 197–208, Feb. 2020, https://doi.org/10.21595/jve.2019.20473

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2019.20473
UR  - https://doi.org/10.21595/jve.2019.20473
TI  - Effect of annulus drilling fluid on lateral vibration of drillstring
T2  - Journal of Vibroengineering
AU  - Li, Lixin
AU  - Yang, Chunxu
AU  - Wang, Rui-He
AU  - Han, Laiju
AU  - Xue, Qilong
PY  - 2020
DA  - 2020/02/15
PB  - JVE International Ltd.
SP  - 197-208
IS  - 1
VL  - 22
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

@article{Li_2020,
	doi = {10.21595/jve.2019.20473},
	url = {https://doi.org/10.21595/jve.2019.20473},
	year = 2020,
	month = {feb},
	publisher = {{JVE} International Ltd.},
	volume = {22},
	number = {1},
	pages = {197--208},
	author = {Lixin Li and Chunxu Yang and Rui-He Wang and Laiju Han and Qilong Xue},
	title = {Effect of annulus drilling fluid on lateral vibration of drillstring},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]L. Li, C. Yang, R.-H. Wang, L. Han, and Q. Xue, “Effect of annulus drilling fluid on lateral vibration of drillstring,” Journal of Vibroengineering, vol. 22, no. 1, pp. 197–208, Feb. 2020, doi: 10.21595/jve.2019.20473.

Copy IEEE

Copied to clipboard!

Li, Lixin, Chunxu Yang, Rui-He Wang, Laiju Han, and Qilong Xue. “Effect of Annulus Drilling Fluid on Lateral Vibration of Drillstring.” Journal of Vibroengineering 22, no. 1 (February 15, 2020): 197–208. https://doi.org/10.21595/jve.2019.20473.

Copy Chicago

Copied to clipboard!

Effect of annulus drilling fluid on lateral vibration of drillstring

Abstract

Highlights

1. Introduction

2. Methods and models

2.1. Basic assumptions

2.2. Derivation of added mass coefficient

3. Results and discussion

3.1. Geometric modeling and mesh generation

3.2. Physical model

3.3. Boundary condition setting

3.4. Verification of grid independence

3.5. Analysis of calculation results

3.6. Relevant verification of internal liquid influence on lateral vibration

4. Conclusions

References

Cited by

About this article

Related Articles