A reduced chemical kinetic mechanism of diesel fuel for HCCI engines

2.1. Skeletal reduction

The importance of reversible reactions that rapidly reach equilibrium was taken as a skeletal reduction criterion, and the formula of the importance index $I_{A,i}$ can be expressed as follows:

The meanings of the parameters $i$, $v_{A,i}$ and ${\omega }_i$ in the formula could be found in reference [8].

Setting a very small number as the threshold value $\xi$, when $I_{A,i}<\xi$, the $i$th elementary reaction will be deemed as unimportant reaction and eliminated.

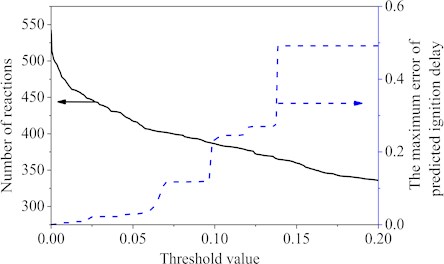
The sampled reduction data came from the auto-ignition results (pressures 10-30 atm, equivalence ratios 0.3-1, temperatures 700 K-1300 K) of the Wang’s mechanism [25]. The c₇h₈, nc₇h₁₆, n₂, o₂, co₂ and h₂o of Wang’s mechanism species were picked out as the important species that cannot be removed. The different threshold values were used to remove the unimportant reactions separately. Fig. 1 showed the curves of the reactions number and the maximum ignition delay time error corresponding to the different threshold values. From the Fig. 1, it was easy to see that when the threshold value increased, the maximum ignition delay time error became larger and the elementary reactions were deleted more. Fig. 1 also showed that 140 reactions were subsequently eliminated using a threshold value of approximately 0.0655, and the maximum error of the first reduction was 7 %. Within the set interval, as the threshold value was greater than 0.0655, the maximum error value would be more than 10 %, so the threshold value was chosen as 0.0655 in the first step.

Fig. 1Number of reactions and the maximum error value under different threshold values

2.2. Time scale reduction

The second step was to get quasi-steady-state species, the criterion of getting the quasi-steady-state species can be written in the following form:

where, $\epsilon$ was the threshold value.

Again using the databases from auto-ignition of the Wang’s mechanism, the quasi-steady-state species can be obtained by using the criterion [26]. Fig. 2 showed the curves of the specie number and the maximum ignition delay time error corresponding to the different threshold values. Choosing $\epsilon =$ 0.005, 32 QSS species, namely ic₈ketab, tc₃h₆o₂hco, ic₃h₇co, ac₈h₁₆ooh-b, ac₈h₁₆ooh-bo₂, nc₃h₇co, ch₂cch₂oh, ac₈h₁₇, nic₄h₉, ch₃co, ac₈h₁₇o₂, ch₂oh, ch, nc₇ket₂₄, c₇h₁₄ooh₂-4, ic₄h₇o, A₁-, tc₄h₉, tc₃h₆cho, ic₄h₅, tc₃h₆o₂cho, ic₃h₇, c₆h₅ch₂o, nc₃h₇, c₆h₄ch₃, ch₂, pc₄h₉, hco, c₇h₁₅-2, c₂h₃co and ic₃h₅co, were obtained. Deleting these QSS species resulted in a final 77-species and 73 global-steps reduced mechanism. From the point of view of ignition delay only, comparing the final mechanism with the original Wang’s mechanism, it was found that the maximum error value of final 77-species mechanism was 7.2 %. Within the set interval, as the threshold value was greater than 0.005, the maximum error value would be more than 10 %, so the threshold value was chosen as 0.005 in the second step.

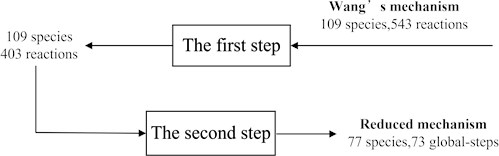
Fig. 3 showed the reduction with two steps. The first step was to remove the 140 unimportant reactions (from 543 reactions to 403 reactions) and the second step was to determine the quasi-steady state components (from 109 species to 77 species). Obviously, the number of species was reduced by one third.

Fig. 2Number of reactions and the maximum error value under different threshold values

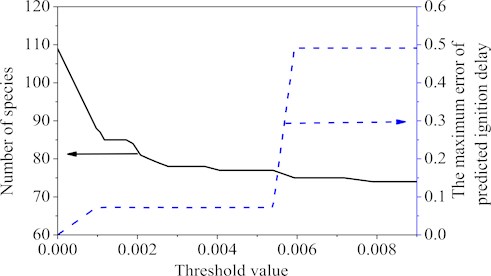
Fig. 3The reduction steps

3.1. Ignition delay time

Fig. 4 showed the $n$-heptane ignition delay curves of Wang’s mechanism and the final 77-species reduced mechanism under the following working conditions: the pressure 40 atm, equivalence ratios 0.5-1 and initial temperatures 700 K-1240 K. No matter high or low temperature, the ignition delay curves of the final reduced mechanism precisely mimicked that of the Wang’s mechanism.

Fig. 4Ignition delay time curves of n-heptane/air mixtures of the Wang’s and reduced mechanisms at various equivalence ratios. Experimental data are obtained from reference [27]

Fig. 5 showed the toluene ignition delay time curves of Wang’s and the final 77-species reduced mechanisms under the following working conditions: the pressure 50 atm, equivalence ratios 0.5-1 and initial temperatures 1000 K-1400 K. It was seen that the very good overlap of the two ignition delay time curves was obtained for the entire parameter range.

Fig. 5Ignition delay time curves of toluene/air mixtures from the Wang’s and reduced mechanisms at various equivalence ratios. Experimental data are obtained from reference [28]

Fig. 6 showed the ignition delay time curves of two component mixture ($n$-heptane and toluene) using the Wang’s and the final 77-species reduced mechanisms under the following working conditions: the pressures 10-50 atm, equivalence ratio 0.3 and initial temperatures 800-1250 K. It was seen that the three curves (10 atm, 30 atm and 50 atm) of the final 77-species reduced mechanism were all approximately identical to that of the Wang’s mechanism for the entire parameter range.

Fig. 6Ignition delay time of toluene/n-heptane/air mixtures from the Wang’s and reduced mechanisms at various pressures. Experimental data are obtained from reference [29]

3.2. Species profiles

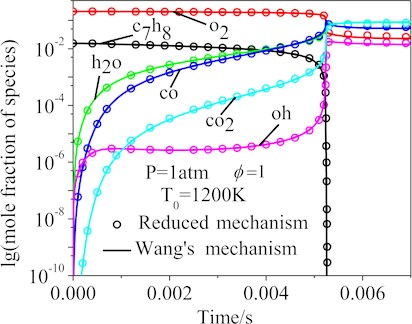
Fig. 7 showed the computed main species mole fraction of the $n$-heptane/toluene/air mixtures using the Wang’s and the final 77-species reduced mechanisms under the following working conditions: the pressure 1 atm, equivalence ratio 1 and initial temperatures 1200 K. The mole fractions curves of the important species of the Wang’s and the final 77-species reduced mechanisms, such as c₇h₈, oh, co, o₂, co₂ and h₂o, were in good agreement.

Fig. 7The calculated concentration changes of the main species using the Wang’s and reduced mechanisms

3.3. Validation in HCCI engines

The key parameters of the HCCI engine, such as, compression ratio, bore, stroke, displacement, connecting rod, etc., were from Reference [30].

The simulation conditions were set as follows: 1. the engine speed of 900 r/min, the incipient temperature of 365 K, the incipient pressure of 2 atm and the equivalence ratio of 0.25; 2. the engine speed of 900 r/min, the incipient temperature of 393 K, the incipient pressure of 1atm and the equivalence ratio of 0.2857.

Fig. 8 showed the cylinder pressure curves of the two simulation conditions by using a single zone model. It was easy to see that under given conditions, the cylinder pressure curves calculated by the Wang’s and the final 77-species reduced mechanisms were almost identical (the maximum error of the conditions 1 and 2 was 4.2 %). It was also easy to see that the maximum cylinder pressure calculated by the Wang’s and the final 77-species reduced mechanisms was larger than the experimental data [30]. The deviations were primarily induced by the adiabatic hypothesis.

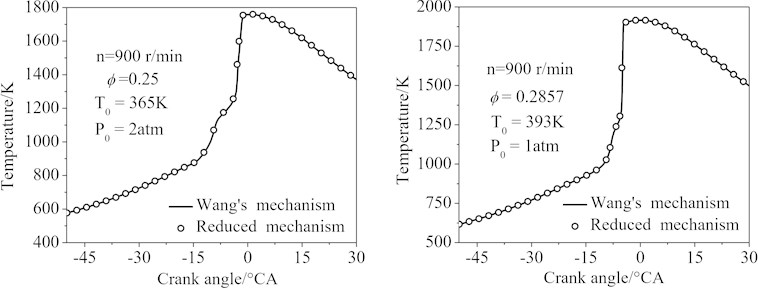
Fig. 9 showed the temperature profiles of the two simulation conditions. It was seen that the curves calculated by the final 77-species reduced mechanism matched that of Wang’s mechanism almost exactly (the maximum error of the conditions 1 and 2 was 6.5 %).

Fig. 8The cylinder pressure of the HCCI engine

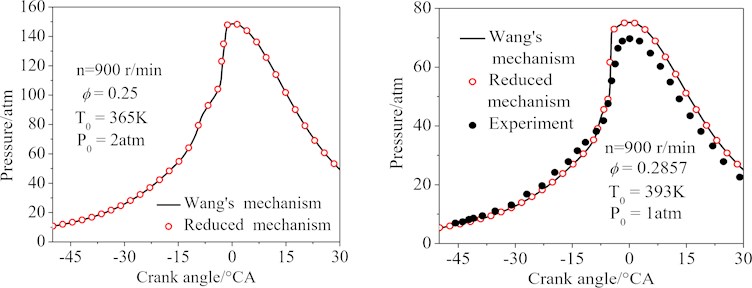
Fig. 9The temperature of the HCCI engine