Buckling of mono-axially compressed rectangular grids

1. Introduction

Grid structures are structural systems extensively used in many engineering applications for their many advantages: (a) they are efficient in transferring concentrated loads, (b) participate as a whole to the load carrying action, (c) are easy to inspect or repair because are open structures.

In the past, grid structures consisting of ribs and skins have been largely studied. Ref. [1] grouped analytical models for grid structures into two categories: exact models, which consider the grid geometry simulating ribs and skin individually, and equivalent models, which smear the grid as a homogenized plate. Grid structures can have different configuration: with or without skins (at the inner and outer surface of the shell), made of composite materials, multiple geometries, and shapes. In recent years, many studies have been carried out on the buckling behavior of reinforced cylindrical shells with cross stiffeners [2]. However, rectangular beam grids are the most common in practice and their buckling load is an important parameter to know.

In this work, the buckling behavior of rectangular beam grids is studied analytically. The critical load of mono-axially compressed rectangular beam grids is derived by using two different models: (i) the Kirchhoff's orthotropic plate, and (ii) a planar system of beams, both axially loaded in-plane. The two models are intrinsically different: the plate is meant as an equivalent model of homogenized continuum, in which the beams “are smeared” on the plate; the frame, instead, preserves the discrete nature of the constituent members. To solve the plate, the classic separation of the variables is adopted; to solve the frame, it is conjectured that the envelope of the buckled beams is a smooth function, so that a variational procedure can be applied.

Indeed, the Rayleigh-Ritz energy method had already been adopted long time ago [3], but it seems to have been forgotten nowadays. Here, the method of Ref. [3] is reproposed with slight changes. On the other hand, several orthotropic plate theories are available in literature [4]-[7]. The Kirchhoff's orthotropic model is chosen here for its simplicity.

The paper is organized as follows. In Section 2 the problem is posed. In Section 3 the Kirchhoff’s orthotropic theory is used for an equivalent plate, and the bifurcation condition is derived. In Section 4 the Rayleigh-Ritz energy method is worked out for the beam assembly, and the relevant critical load is computed. In Section 5 some parametric studies are carried out and the analytical solutions are validated by comparison with numerical Finite Element results. Finally, in Section 6 some conclusions are drawn.

2. Problem position

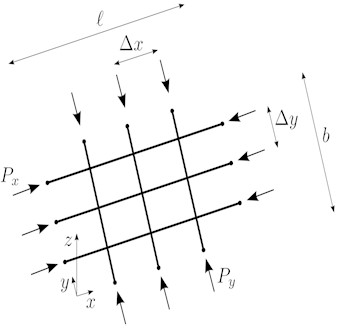
A rectangular $\mathcal{l}\times b$ beam grid with rectangular $\mathrm{\Delta }x\times \mathrm{\Delta }y$ mesh is considered (see Fig. 1). The grid is composed of two orders of continuous beams, simply supported at the ends. The $x$-direction and $y$-direction beams are prestressed by forces $P_x$ and $P_y$, respectively, positive when they generate compression. Therefore, in general, the grid is biaxially prestressed. $p$ and $q$ are the numbers of beams in $x$-direction and in $y$-direction, respectively. It is consequently $\mathcal{l}/\mathrm{\Delta }x=q+1$ and $b/\mathrm{\Delta }y=p+1$. Each order of beams consists of equal beams of uniform section. The flexural and torsional stiffness of the single beam in $i$-direction are denoted by $E{I}_i$ and $G{J}_i$, respectively.

Fig. 1Beam grid

3. Equivalent orthotropic plate model

A rectangular Kirchhoff’s orthotropic plate, simply supported on the whole contour is considered. The plate is monoaxially prestressed by forces $p_x$ uniformly distributed and normal to the edges. Denoting by $w\left(x,y\right)$ the out of plane displacement of the point $\left(x,y\right)$, the indefinite equilibrium equation is written as:

where $D_i\left(i=x,y\right)$ and $H$ are the flexural and the torsional stiffnesses of the plate, respectively. They are evaluated by enforcing energy equivalences between the plate and the grid, and turn out to be equal to:

A linear combination with unknown coefficients of products of sinusoidal functions is used as trial functions, namely:

where $A_{nm}$ are unknown coefficients and $n$, $m$ are integer numbers, even unknowns. Each term of the series describes a deformation in which the plate bends in $n$ half-waves (of length $\mathcal{l}/n$) in the $x$-direction and $m$ half-waves (of length $b/m$) in the $y$-direction. Denoting by $\alpha ≔\mathcal{l}/b$ the aspect ratio and substituting Eq. (3) in Eq. (1), ${\infty }^2$ critical loads are found, each associated with the pair $\left(n,m\right)$, i.e:

Since we are interested in the smallest of these loads, we need to minimize $p_{xc}\left(n,m\right)$ with respect to the two variables. Accordingly, $m=1$ must be taken, while $n$ must be determined by trial and error. By letting $\delta ≔D_x/D_y$, $\gamma ≔H/D_y$ and $p_{xc}={\mu }_{xc}{\pi }^2{D}_x/b^2$, the nondimensional critical load ${\mu }_{xc}$ is determined as:

It is observed that, when $\alpha$ is an integer, the minimum critical load occurs at $n=\alpha$, and it is equal to ${\mu }_{xc,min}=1+2\frac{\gamma \hspace{0.17em}}{\delta }+\frac{1}{\delta }.$The same limit value is found for any $\alpha$ sufficiently large. When the plate is isotropic (i.e., when $\delta =\gamma =1$), then, the well-known value ${\mu }_{xc,min}=4$ is recovered.

4. Beam assembly model

The grid is considered as an assembly of beams undergoing flexure and torsion. It is conjectured that, in the buckled configuration, the beams lie on a smooth surface $w=w(x,y)$, which is still given by Eq. (3), so that, by using the Raileigh-Ritz model, the problem can be solved in closed-form.

The Total Potential Energy (TPE) of the grid is defined as sum of flexural ($f$), torsional ($t$) and geometric ($g$) energy of the two orders of beams, $\mathrm{\Pi }={\mathrm{\Pi }}_x^f+{\mathrm{\Pi }}_y^f+{\mathrm{\Pi }}_{xy}^t+{\mathrm{\Pi }}_x^g+{\mathrm{\Pi }}_y^g$.

By accounting for ${\theta }_x=w_{,y}$, ${\theta }_y=w_{,x}$, the single energy terms read:

Assume, for simplicity's sake, that $E{I}_x=E{I}_y=EI$ and $G{J}_x=G{J}_y=GJ$. By imposing stationarity of the TPE, the equilibrium equation follows, from which the buckling critical load is derived as:

where, $\rho ≔P_y/P_x$ is the ratio between the magnitudes of the two loads and $n$, $m$ are the values which minimize $P_{xc}$. In the special case of $\rho =0$, by introducing the dimensionless parameters $\mathrm{\Delta }\xi ≔\mathrm{\Delta }x/\mathcal{l}$, $\mathrm{\Delta }\eta ≔\mathrm{\Delta }y/b$ and by letting $\alpha ≔l/b$ the aspect ratio of the grid, $\beta =GJ/EI$ the torsional-to-flexural stiffness ratio, and $P_{xc}={\mu }_{xc}{\pi }^{2}EI/b^2$, the critical nondimensional load ${\mu }_{xc}$ is determinated:

It should be noticed that when $m=p+1$, Eq. (8) becomes indeterminate, because the flexural and prestress energies are zero (indeed, the beams are located at the nodal lines of the deformed configuration).

5. Numerical results

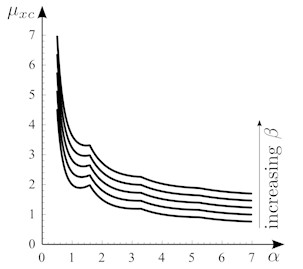
A parametric study is carried out by using the beam assembly model (Eq. (8)). Since ${\mu }_{xc}={\mu }_{xc}(∆\xi ,∆\eta ,\alpha ,\beta ,n,m)$, as a first analysis, $∆\xi$, $∆\eta$ are fixed and ${\mu }_{xc}$ (minimized with respect to $n,m$) plotted vs the aspect ratio $\alpha$ for different stiffness ratios $\beta$ (Fig. 2(a)). The classic signature curves, typical of homogeneous and isotropic plates, is obtained. However, differently from those, it is observed that the critical load slowly decreases with $\alpha$. This result can be interpreted by making use of the equivalent plate model. Indeed, since the nondimensional steps $∆\xi$, $∆\eta$ are kept constants, also the number of beams parallel to the $x$ and $y$-direction are constant, so that, while the aspect ratio increases, the equivalent stiffnesses per unit length of the plate decrease, entailing a decreasing of the critical load.

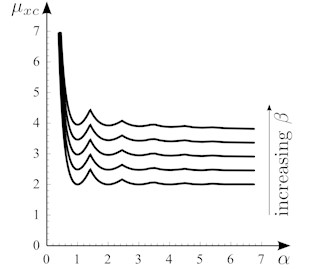
As a second analysis, only $∆\eta$ is kept constant, while the $\mathrm{\Delta }\xi =\hspace{0.17em}\mathrm{\Delta }\eta /\alpha$ is taken, thus obtaining the plot in Fig. 2(b). It is seen that the critical load now tends to an asymptotic value for large $\alpha$. Indeed, the case analyzed is representative of a family of grids in which the width $b$ is kept constant together with the number of beams in the $x$-direction, while the length $\mathcal{l}$ is increased, together with the number of beams in the $y$-direction, to keep their dimensional step $\mathrm{\Delta }x$ constant. Again, by resorting to the equivalent plate model, since the plate stiffnesses per unit length are equal for any member of the family, the tendency to an asymptotic value is consistently observed.

Fig. 2Frame model nondimensional critical load of the rectangular grid, subject to mono-axial compression vs the aspect ratio α, for β=0,…,1: a) Δξ=Δη=0.09; b) Δη=0.01, Δξ= Δη/α

a)

b)

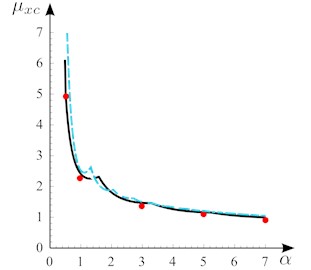
The analytical results are compared with a Finite Element analysis for validation. The FE model is made of an assembly of Euler-Bernoulli beams. Constraints at the ends do not permit $z$-displacements for all the beams, and $x$- and $y$-displacement for beams in the $y$ and $x$-directions, respectively. The loads are applied as concentrated forces at the ends of the beams, directed as the beam longitudinal axes (see Fig. 1). One of the (analytical) curves in Figs. 2(a) and 2(b) is compared in Figs. 3(a) and 3(b) with FE results, and a very good agreement is found. In the same figures, the results provided by the Kirchhoff’s orthotropic plate theory (Eq. (5)) are also reported; they turn out to be close to those relevant to the assembly beam model.

Fig. 3Nondimensional critical load of the rectangular grid, subject to mono-axial compression vs the aspect ratio α, for β= 0.25: a) Δξ=Δη=0.09; b) Δη=0.01, Δξ= Δη/α. Rayleigh-Ritz energy method (solid black line), Kirchhoff's orthotropic plate theory (dashed cyan line), FE analysis (dots)

a)

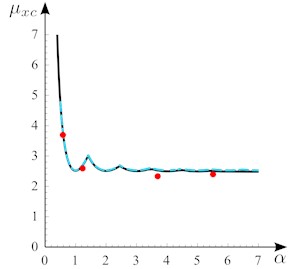
b)

As a third analysis, a study is performed, in which the dimension $b$, $\mathcal{l}$ of the grid are kept constant, while the number of beams is increased. Fig. 4 compares the two analytical model with FE results. It refers to a square dominion ($b=\mathcal{}\mathcal{l}$) with an equal number of beams ($p=q$). It is seen that when the number of beams is sufficiently large (e.g., $q=\text{9}$, corresponding to $\mathrm{\Delta }\eta =\text{0.1}$) the error is reasonable (about 6 %), and tends to zero with $q$. However, when $q$ is smaller, the grid model gives a result better than the homogenized plate.

Fig. 4Comparison of results: a) nondimensional critical load of the rectangular grid, subject to mono-axial compression vs the number of beams q=p, for β=0.25; b) percentage error (PE) from FE results. Rayleigh-Ritz energy method (blue), Kirchhoff's orthotropic plate theory (magenta), FE analysis (dots)

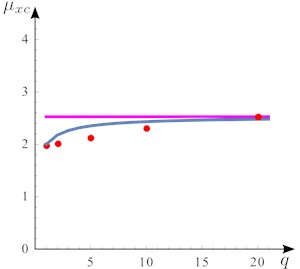
a)

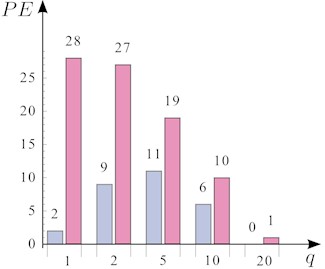
b)

6. Conclusions

A buckling analysis of a simply supported rectangular grid, subject to mono-axial compression, was carried out. Two models were used: (a) a homogenized Kirchhoff’s orthotropic plate, and (b) an assembly of beams tackled via an energy method. Analytical results were compared with Finite Element analyses. The following conclusions were drawn.

1) The Rayleigh-Ritz energy method supplies results in good agreement with FE models for all the cases analyzed.

2) The Kirchhoff's orthotropic plate model is also in good agreement with FE results only when the number of beams is sufficiently large.

The results should be important to the research, since based on analytical solutions that, unlike the numerical approaches, allow to study the influence of the parameters without redoing the model. The main contribution of this study is the interpretation of the grid mechanical behavior. Indeed, it has been proven here, that the surface enveloping the buckled grid is close to that describing the buckling of a homogeneous plate, while giving better results.