Differential quadrature method (DQM) for studying initial imperfection effects and pre- and post-buckling vibration of plates

Makvandi, Hesam; Moradi, Shapour; Poorveis, Davood; Heidari Shirazi, Kourosh

doi:10.21595/jve.2017.18252

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 February 2018

Check for updates

Differential quadrature method (DQM) for studying initial imperfection effects and pre- and post-buckling vibration of plates

Hesam Makvandi¹

Shapour Moradi²

Davood Poorveis³

Kourosh Heidari Shirazi⁴

^{1, 2, 3, 4}Shahid Chamran University of Ahvaz, Faculty of Engineering, Ahvaz, Iran

Corresponding Author:

Shapour Moradi

Cite the article Download PDF

Downloads 2174

WoS Core Citations 2

CrossRef Citations 2

Abstract

The effects of initial geometric imperfection and pre- and post-buckling deformations on vibration of isotropic rectangular plates under uniaxial compressive in-plane load have been studied. The differential equations of plate motions, using the Mindlin theory and Von-Karman stress-strain relations for large deformations, were extracted. The solution of nonlinear differential equations was assumed as the summation of dynamic and static solutions. Due to a large static plate deflection as compared with its vibration amplitude, the differential equations were solved in two steps. First, the static equations were solved using the differential quadrature method and the arc-length strategy. Next, considering small vibration amplitude about the deformed shape and eliminating nonlinear terms, the natural frequencies were extracted using the differential quadrature method. The results for different initial geometric imperfection and different boundary conditions reflect the impact of the mentioned factors on the natural frequencies of plates.

1. Introduction

Because of the high strength-to-weight ratio, plates have been widely used in various industrial applications. Due to this widespread use, the vibrations of thin-walled structures have been investigated by many researchers and still attract more attention. Numerous studies in vibration analysis of plates and shells with different shapes and boundary conditions were conducted. Nevertheless, there are some differences between the theoretical and experimental results that could be caused by the geometrical imperfection or structural deformations in the case of a loaded structure. Therefore, some researchers focused on the effect of initial imperfection and pre- and post-buckling deformations on the dynamic behavior of plates.

The effects of geometric imperfections on vibrations of uniaxial and biaxial compressed rectangular plates were studied by Hui and Leissa [1]. Ilanko and Dickinson [2] and Ilanko [3] investigated the vibration of geometrically imperfect and simply supported rectangular plates under uni-axial loading in the pre- and post-buckled state using the Galerkin method. NG and White [4] developed the Rayleigh-Ritz and finite element methods to study the effects of pre- and post-buckling deformations on natural frequencies of uniaxial isotropic rectangular plates. They concluded that by increasing the load, the fundamental frequency of plate decreases in the pre-buckling state and increases in the postbuckling state. Employing analytical methods, Pasic and Herrmann [5] extracted the non-linear free vibration frequencies of buckled plates with deformable loaded edges.

The Galerkin method was used by Sassy and Ostigu [6] to compute the effects of initial imperfection on postbuckling and vibration frequencies of plates. They observed that responses heavily depended on the initial imperfection amplitude and boundary conditions. The finite difference method was implemented by Williams et al. [7] to solve the postbuckling equations of circular plates. They employed the lumped mass modeling method to study the vibration of plates around their buckled shape.

The Galerkin method was also used by Girish and Ramachandra [8] to investigate post-buckling and vibration of composite plates, subjected to thermal loads and initial geometric imperfections. Li et al. [9] studied the nonlinear vibration of thermally post-buckled orthotropic circular plates. They obtained two sets of coupled ordinary differential equations; one for the thermal post-buckling, and the other for linear vibrations of the plate about the post-buckled configuration. These sets are solved numerically using the shooting method. Panda and Singh [10, 11] evaluated the thermal post-buckling strength of a laminated composite shell panel with the help of the finite element method. They assumed that the structural buckling is caused by thermal loads. They used the Green-Lagrange strain-displacement relations of the higher-order shear deformation theory.

To the best of authors’ knowledge, the dynamic behavior of geometrically imperfect plates considering shear deformations and different boundary conditions using the differential quadrature method has not been yet investigated. Therefore, this study considers effects of initial imperfection and pre- and post-buckling deformations on natural frequencies and modal shapes of uniaxially loaded rectangular isotropic plates. The governing differential equations of the plate are derived applying the Mindlin theory considering the Von-Karman stress-strain relations. The solution includes two steps. In the first step, static nonlinear differential equations transform to a system of nonlinear algebraic equations using the differential quadrature method and then they will be solved using the arc-length strategy. Then, after assuming small amplitude vibration about buckled shape and eliminating the non-linear terms, the differential quadrature method will be applied to the linearized differential equations of motion and to the corresponding boundary conditions. The natural frequencies and mode shapes of the buckled plate could be determined by solving the resulting eigenvalue problem.

2. Governing equations

Using the Mindlin theory and considering the effect of initial geometric imperfection in the Von-Karman strain-displacement relations, the midplane strains of a plate with dimensions shown in Fig. 1 could be obtained. Fig. 1 shows the geometry of a thin rectangular plate with the length $a$ width $b$ , and thickness $h$ . There is a geometrical imperfection in the form of the plate first buckling mode shape with the amplitude $w_{0}$ . The plate is under uniaxial compression $P$ acting across its width:

1

ε_{x} = \frac{\partial u}{\partial x} + z \frac{\partial α}{\partial x} + \frac{1}{2} {(\frac{\partial w}{\partial x})}^{2} + \frac{\partial w}{\partial x} \frac{\partial w_{0}}{\partial x}, ε_{y} = \frac{\partial v}{\partial y} + z \frac{\partial β}{\partial y} + \frac{1}{2} {(\frac{\partial w}{\partial y})}^{2} + \frac{\partial w}{\partial y} \frac{\partial w_{0}}{\partial y},

ε_{z} = 0,

γ_{x y} = \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} + z \frac{\partial α}{\partial y} + z \frac{\partial β}{\partial x} + \frac{\partial w}{\partial x} \frac{\partial w}{\partial y} + \frac{\partial w}{\partial x} \frac{\partial w_{0}}{\partial y} + \frac{\partial w}{\partial y} \frac{\partial w_{0}}{\partial x},

γ_{x z} = (\frac{\partial w}{\partial x} + α), γ_{y z} = (\frac{\partial w}{\partial y} + β),

where $u$ , $v$ and $w$ are displacements in the $x$ , $y$ and $z$ directions, and $α$ and $β$ are rotations about the $x$ and $y$ axis, respectively. The stress relations for homogenous plates are given by:

2

σ_{x x} = \frac{E}{1 - ν^{2}} (ε_{x x} + ν ε_{y y}), σ_{y y} = \frac{E}{1 - ν^{2}} (ε_{y y} + ν ε_{x x}),

σ_{z z} = \frac{E}{1 - ν^{2}} (ν ε_{x x} + ν ε_{y y}), τ_{x y} = \frac{E}{2 (1 + ν)} (γ_{x y}),

τ_{x z} = \frac{E}{2 (1 + ν)} (γ_{x z}), τ_{y z} = \frac{E}{2 (1 + ν)} (γ_{y z}),

where $E$ is the Young’s modulus of elasticity and $ν$ is the Poisson’s ratio. Using Eqs. (1) and (2), the resultant forces and moments (Fig. 2) can be obtained as:

3

[\{\begin{array}{l} N_{x} \\ N_{y} \\ N_{x y} \end{array}\}, \{\begin{array}{l} M_{x} \\ M_{y} \\ M_{x y} \end{array}\}] = \int_{- \frac{h}{2}}^{\frac{h}{2}} \{\begin{array}{l} σ_{x x} \\ σ_{y y} \\ τ_{x y} \end{array}\} (1, z) d z, [\{\begin{array}{l} Q_{x} \\ Q_{y} \end{array}\}] = \int_{- \frac{h}{2}}^{\frac{h}{2}} \{\begin{array}{l} τ_{x z} \\ τ_{y z} \end{array}\} d z .

Fig. 1Rectangular plate under uniaxial in plane compressive load

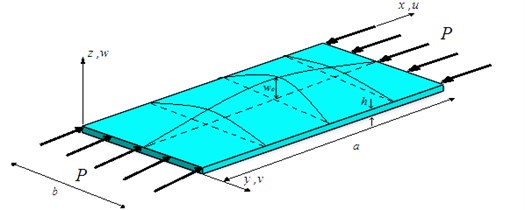
Fig. 2Forces and moments on plate element

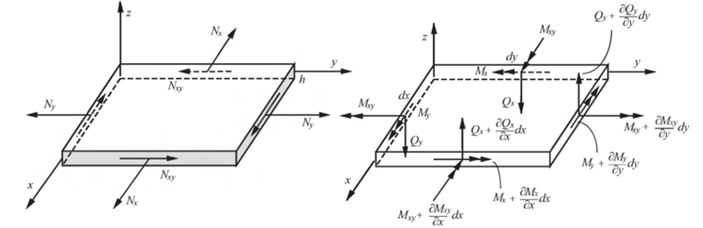
The governing differential equations of motion for the element depicted in Fig. 2 can be written as:

4

\frac{\partial N_{x}}{\partial x} + \frac{\partial N_{x y}}{\partial y} = μ \frac{\partial^{2} u}{\partial t^{2}},

5

\frac{\partial N_{x y}}{\partial x} + \frac{\partial N_{y}}{\partial y} = μ \frac{\partial^{2} v}{\partial t^{2}},

6

\frac{\partial^{2} M_{x}}{\partial x^{2}} + 2 \frac{\partial^{2} M_{x y}}{\partial x \partial y} + \frac{\partial^{2} M_{y}}{\partial y^{2}}

= μ \frac{\partial^{2} w}{\partial t^{2}} - (N_{x} \frac{\partial^{2} (w + w_{0})}{\partial x^{2}} + 2 N_{x y} \frac{\partial^{2} (w + w_{0})}{\partial x \partial y} + N_{y} \frac{\partial^{2} (w + w_{0})}{\partial y^{2}}),

7

\frac{\partial M_{x}}{\partial x} + \frac{\partial M_{x y}}{\partial y} - Q_{x} = I_{x} \frac{\partial^{2} α}{\partial t^{2}},

8

\frac{\partial M_{x y}}{\partial x} + \frac{\partial M_{y}}{\partial y} - Q_{y} = I_{y} \frac{\partial^{2} β}{\partial t^{2}},

where $μ = ρ h$ . $ρ$ is the plate density, and $I_{x} = I_{y} = ρ h^{3} / 12$ . Substituting obtained forces and moments into Eqs. (4-8), one can obtain the nonlinear differential equations of motions in term of displacements. This nonlinear system of differential equations can be solved using the differential quadrature method.

3. Initial imperfection

As already mentioned earlier, the initial geometric imperfection could cause difference between the experimental and theoretical behaviors of plates. In the current study, the geometrical imperfections are presented in terms of the first buckling modal shape of the plate. Table 1 represents the initial imperfection functions used for the various boundary conditions.

Table 1Initial geometric imperfection functions

Boundary condition	Initial geometric imperfection
SSSS	$w_{0} = W_{0} (s i n \frac{n π x}{a}) (s i n \frac{n π y}{b})$
CCCC	$w_{0} = W_{0} (1 - c o s \frac{2 n π x}{a}) (1 - c o s \frac{2 n π y}{b})$
CSCS (Loaded clamped sides)	$w_{0} = W_{0} (1 - c o s \frac{2 n π x}{a}) (s i n \frac{n π y}{b})$
SCSC (Loaded simply supported sides)	$w_{0} = W_{0} (s i n \frac{n π x}{a}) (1 - c o s \frac{2 n π y}{b})$

To investigate the effects of initial imperfection on natural frequencies of a rectangular plate, the governing equations are solved in no-load condition. Hence, the nonlinear terms in these equations are neglected. The DQ method application to the resultant equations and their corresponding boundary conditions results in the following eigenvalue problem:

9

[\begin{array}{l} A_{B B} & A_{B I} \\ A_{I B} & A_{I I} \end{array}] \{\begin{array}{l} X_{B} \\ X_{I} \end{array}\} = - ω^{2} [\begin{matrix} 0 & 0 \\ B_{I B} & B_{I I} \end{matrix}] \{\begin{array}{l} X_{B} \\ X_{I} \end{array}\},

where $X_{B}$ and $X_{I}$ are displacement vectors of boundary and interior points, respectively. The natural frequencies and modal shapes of the plate can be extracted from the solution of the eigenvalue problem.

4. Post-buckling

As it has already been mentioned, the deformation of plate under compressive in plane load can change its dynamic behavior. In order to evaluate this effect, natural frequencies of rectangular plate under uniaxial in-plane load are calculated using governing equations. To solve these equations, the solution is considered as a summation of static (time-independent solution) and dynamic ones (time-dependent solution). This represents the plate vibration about the deformed shape. Therefore, the solution can be written as:

10

w = w_{s} + w_{d}, u = u_{s} + u_{d}, v = v_{s} + v_{d}, α = α_{s} + α_{d}, β = β_{s} + β_{d},

where $w_{s}$ , $u_{s}$ , $v_{s}$ , $α_{s}$ and $β_{s}$ are the postbuckling static responses and $w_{d}$ , $u_{d}$ , $v_{d}$ , $α_{d}$ and $β_{d}$ are the dynamic responses about the buckled shape. Substituting Eq. (10) in the governing equations and eliminating the time-dependent terms the plate buckling equations can be obtained.

In the process of solution of these nonlinear differential equations, they will be converted to a set of nonlinear algebraic equations using the DQ method. then, the resultant equations and their corresponding boundary conditions will be solved using the arc-length method. If one uses the Newton-Raphson method to solve these equations, the load will control the path. In other words, the load increases with fixed load steps while displacements are unknown. This algorithm usually is not able to pass the bifurcation point, therefore, it is required to use the arc-length method, where the load is considered as a variable along with the displacement and a constraint on the load increase is used [14-16].

5. Pre- and post-buckling vibration

After solving static equilibrium equations in the first step, the result will be replaced in the differential equations of motion of the buckled plate. Eliminating the nonlinear time-dependent terms and the terms which only depend on the static response, the results will be obtained in the form of the following equations:

11

\frac{E h}{1 - ν^{2}} [\begin{matrix} u_{d, x x} + w_{s, x x} w_{d, x} + w_{d, x x} w_{s, x} + w_{d, x x} w_{0, x} + w_{d, x} w_{0, x x} \\ + ν (v_{d, x y} + w_{d, x y} w_{s, y} + w_{s, x y} w_{d, y} + w_{d, x y} w_{0, y} + w_{d, y} w_{0, x y}) \end{matrix}]

+ \frac{E h}{2 (1 + ν)} [\begin{matrix} u_{d, y y} + v_{d, x y} + w_{d, x y} w_{s, y} + w_{s, x y} w_{d, y} + w_{s, x} w_{d, y y} \\ + w_{d, x} w_{s, y y} + w_{0, x y} w_{d, y} + w_{0, x} w_{d, y y} + w_{d, x y} w_{0, y} + w_{d, x} w_{0, y y} \end{matrix}] = μ {\ddot{u}}_{d},

12

\frac{E h}{1 - ν^{2}} [\begin{matrix} v_{d, y y} + w_{d, y y} w_{s, y} + w_{s, y y} w_{d, y} + w_{d, y y} w_{0, y} + w_{d, y} w_{0, y y} \\ + ν (u_{d, x y} + w_{d, x y} w_{s, x} + w_{s, x y} w_{d, x} + w_{d, x y} w_{0, x} + w_{d, x} w_{0, x y}) \end{matrix}]

+ \frac{E h}{2 (1 + ν)} [\begin{matrix} u_{d, x y} + v_{d, x x} + w_{d, x y} w_{s, x} + w_{s, x y} w_{d, x} + w_{s, x} w_{d, x y} \\ + w_{d, x} w_{s, x y} + w_{0, x x} w_{d, y} + w_{0, x} w_{d, x y} + w_{d, x x} w_{0, y} + w_{d, x} w_{0, x y} \end{matrix}] = μ {\ddot{v}}_{d},

13

K_{s} G h (α_{d, x} + w_{d, x x}) + K_{s} G h (β_{d, y} + w_{d, y y}) + \frac{E h}{1 - ν^{2}} (u_{d, x x} w_{s, x} + u_{s, x x} w_{d, x}

+ w_{d, x x} w_{s, x}^{2} + 2 w_{s, x x} w_{s, x} w_{d, x} + w_{d, x x} w_{0, x} w_{s, x} + w_{s, x x} w_{0, x} w_{d, x} + 2 w_{s, x} w_{d, x} w_{0, x x}

+ ν (v_{d, x y} w_{s, x} + v_{s, x y} w_{d, x} + w_{d, x y} w_{s, x} w_{0, y} + w_{s, x y} w_{d, x} w_{0, y} + w_{0, x y} w_{d, x} w_{s, y}

+ w_{0, x y} w_{s, x} w_{d, y})) + \frac{E h}{1 - ν^{2}} (u_{d, x x} w_{0, x} + w_{d, x x} w_{0, x} w_{s, x} + w_{s, x x} w_{0, x} w_{d, x} + w_{d, x x} w_{0, x}^{2}

+ w_{0, x x} w_{0, x} w_{d, x} v + ν (v_{d, x y} w_{0, x} + w_{d, x y} w_{0, x} w_{s, y} + w_{s, x y} w_{0, x} w_{d, y} + w_{d, x y} w_{0, x} w_{0, y}

+ w_{0, x y} w_{0, x} w_{d, y})) + \frac{E h}{1 - ν^{2}} (u_{d, x} w_{s, x x} + u_{s, x} w_{d, x x} + \frac{1}{2} w_{s, x}^{2} w_{d, x x} + w_{s, x x} w_{s, x} w_{d, x}

+ w_{s, x x} w_{0, x} w_{d, x} + w_{d, x x} w_{0, x} w_{s, x} + ν (v_{d, y} w_{s, x x} + v_{s, y} w_{d, x x} + \frac{1}{2} w_{s, y}^{2} w_{d, x x}

+ w_{d, y} w_{s, x x} w_{0, y} + w_{s, y} w_{d, x x} w_{0, y} + w_{s, y} w_{s, x x} w_{d, y})) + \frac{E h}{1 - ν^{2}} (u_{d, x} w_{0, x x}

+ w_{0, x x} w_{0, x} w_{d, x} + ν (v_{d, y} w_{0, x x} + w_{d, y} w_{0, x x} w_{0, y})) + \frac{E h}{1 - ν^{2}} (v_{d, y y} w_{s, y} + v_{s, y y} w_{d, y}

+ w_{d, y y} w_{s, y}^{2} + 2 w_{s, y y} w_{0, y} w_{d, y} + w_{d, y y} w_{0, y} w_{s, y} + w_{s, y y} w_{0, y} w_{d, y} + 2 w_{s, y} w_{d, y} w_{0, y y}

+ ν (u_{d, x y} w_{s, y} + u_{s, x y} w_{d, y} + w_{s, x y} w_{o, x} w_{d, y} + w_{s, x y} w_{d, y} w_{0, x} + w_{d, x y} w_{s, y} w_{0, x}

+ w_{0, x y} w_{s, x} w_{d, y} + w_{s, x y} w_{d, y} w_{s, x})) + \frac{E h}{1 - ν^{2}} (v_{d, y y} w_{0, y} + w_{d, y y} w_{0, y} w_{s, y}

+ w_{s, y y} w_{0, y} w_{d, y} + w_{d, y y} w_{0, y}^{2} + w_{0, y y} w_{0, y} w_{d, y}_ν (u_{d, x y} w_{0, y} + w_{d, x y} w_{0, y} w_{s, x} v

+ w_{s, x y} w_{0, y} w_{d, x} + w_{d, x y} w_{0, x} w_{0, y} + w_{0, x y} w_{0, y} w_{d, x})) + \frac{E h}{1 - ν^{2}} (u_{d, x} w_{0, x x}

+ w_{0, x x} w_{s, x} w_{d, x} + w_{0, x x} w_{s, x} w_{d, x} + ν (v_{d, y} w_{0, x x} + w_{0, x x} w_{s, y} w_{d, y}

+ w_{0, x x} w_{0, y} w_{d, y}) + \frac{E h}{1 - ν^{2}} (v_{d, y} w_{s, y y} + v_{s, y} w_{d, y y} + \frac{1}{2} w_{d, y y} w_{s, y}^{2} + w_{s, y y} w_{d, y} w_{s, y}

+ w_{d, y y} w_{s, y} w_{0, y} + w_{d, y} w_{s, y y} w_{s, y} v + ν (u_{s, x} w_{d, y y} + u_{d, x} w_{s, y y} + \frac{1}{2} w_{d, y y} w_{s, x}^{2}

+ w_{d, x} w_{s, y y} w_{0, x} + w_{s, x} w_{d, y y} w_{0, x})) + \frac{E h}{1 - ν^{2}} (v_{d, y} w_{0, y y} + w_{0, y y} w_{s, y} w_{d, y}

+ w_{0, y y} w_{0, y} w_{d, y} + ν (u_{d, x} w_{0, y y} v + w_{d, x} w_{0, y y} w_{s, x} + w_{d, x} w_{0, y y} w_{0, x})

+ \frac{E h}{2 (1 + ν)} (u_{s, x y} w_{d, y} + u_{d, x y} w_{s, y} + v_{s, x x} w_{d, y} + v_{d, x x} w_{s, y} + w_{d, x x} w_{s, y}^{2}

+ 2 w_{s, x x} w_{s, y} w_{d, y} + 2 w_{0, x x} w_{s, y} w_{d, y} + w_{s, x y} w_{d, x} w_{s, y} + w_{s, x y} w_{d, x} w_{s, y}

+ w_{d, x y} w_{s, x} w_{s, y} + w_{s, x y} w_{s, x} w_{d, y} + w_{d, x y} w_{0, x} w_{s, y} + w_{0, x} w_{s, x y} w_{d, y}

+ w_{s, x x} w_{0, y} w_{d, y} + w_{d, x x} w_{0, y} w_{s, y} + w_{0, x y} w_{s, y} w_{d, x} + w_{0, x y} w_{s, x} w_{d, y}))

+ \frac{E h}{2 (1 + ν)} (u_{d, x y} w_{0, y} + v_{d, x x} w_{0, y} + w_{s, x x} w_{d, y} w_{0, y} + w_{d, x x} w_{s, y} w_{0, y} + w_{s, x y} w_{d, x} w_{0, y}

+ w_{d, x y} w_{s, x} w_{0, y} + w_{0, x y} w_{d, y} w_{0, y} + w_{d, x y} w_{s, y} w_{0, y} + w_{d, x y} w_{0, x} w_{0, y} + w_{d, x x} w_{0, y}^{2}

+ w_{0, x y}^{2} w_{0, y} w_{d, x})) + \frac{E h}{2 (1 + ν)} (u_{d, y y} w_{s, x} + u_{s, y y} w_{d, x} + v_{s, x y} w_{d, x} + v_{d, x y} w_{s, x}

+ w_{s, x y} w_{s, x} w_{d, y} + w_{s, x y} w_{d, x} w_{s, y} + w_{d, x y} w_{s, x} w_{s, y} + w_{d, y y} w_{s, x}^{2} + 2 w_{s, y y} w_{d, x} w_{s, x}

+ w_{d, x y} w_{s, x} w_{0, y} + w_{s, x y} w_{d, x} w_{0, y} + w_{d, y y} w_{s, x}^{2} + w_{0, x y} w_{s, x} w_{d, y} + w_{0, x y} w_{d, x} w_{s, y}

+ w_{d, y y} w_{0, x} w_{s, x} + w_{d, x} w_{0, x} w_{s, y y} + 2 w_{s, y y} w_{d, x} w_{s, y})) + \frac{E h}{2 (1 + ν)} (u_{d, y y} w_{0, x}

+ v_{d, x y} w_{0, x} + w_{d, x y} w_{0, x} w_{s, y} + w_{s, x y} w_{0, x} w_{d, x} + w_{s, y y} w_{0, x} w_{d, x} + w_{d, y y} w_{0, x} w_{s, x}

+ w_{d, y y} w_{0, x}^{2} + w_{d, x y} w_{0, x} w_{0, y} + w_{0, y y} w_{d, x} w_{0, x} + w_{d, y} w_{0, x y} w_{0, x}))

+ \frac{E h}{(1 + ν)} (u_{s, y} w_{d, x y} + u_{d, y} w_{s, x y} + v_{s, x} w_{d, x y} + v_{d, x} w_{s, x y} + w_{d, x y} w_{s, x} w_{s, y}

+ w_{s, x y} w_{d, x} w_{s, y} + w_{s, x y} w_{s, x} w_{d, y} + w_{d, x y} w_{0, x} w_{s, y} + w_{s, x y} w_{0, x} w_{d, y}

+ w_{s, x y} w_{d, x} w_{0, y} + w_{d, x y} w_{s, x} w_{0, y})) + \frac{E h}{(1 + ν)} (u_{d, y} w_{0, x y} + v_{d, x} w_{0, x y}

+ w_{0, x y} w_{s, x} w_{d, y} + w_{0, x y} w_{d, x} w_{s, y} + w_{0, x y} w_{0, x} w_{d, y} + w_{0, x y} w_{d, x} w_{0, y})) = μ {\ddot{w}}_{d} .

14

\frac{E h^{3}}{12 (1 - ν^{2})} (α_{d, x x} + ν β_{d, x y}) + \frac{E h^{3}}{24 (1 + ν)} (α_{d, y y} + β_{d, x y}) - K_{s} G h (α_{d} + w_{d, x}) = I_{x} {\ddot{α}}_{d},

15

\frac{E h^{3}}{12 (1 - ν^{2})} (β_{d, x x} + ν α_{d, x y}) + \frac{E h^{3}}{24 (1 + ν)} (α_{d, x y} + β_{d, x x}) - K_{s} G h (β_{d} + w_{d, y}) = I_{y} {\ddot{β}}_{d},

The DQ method is also used to discretize these equations and corresponding boundary conditions which result in a system of eigenvalue equations. The solution of this eigenvalue problem provides the natural frequencies and modal shapes of buckled plate.

6. Results

In this section, with the aim of the accuracy and reliability verification for the proposed method, the developed formulation will be used to investigate several case studies. Using the presented method, the natural frequencies of a simply supported square plate for different initial imperfection amplitudes are calculated without any external compressive load. The results are compared with those obtained from the FEM in Fig. 3. The plate is 1000 mm long, 1000 mm wide, and 10 mm thick. The elasticity modulus, Poisson’s ratio and density of the plate are 200 GPa, 0.3 and 7800 Kg/m³, respectively. The results are compared with those of the commercial software package for finite element analyses. The FEM model consists of 100 shell elements. As it can be seen in figure 3, DQ results and FEM results are in a very good agreement. Furthermore, the figure shows that an increase in the initial imperfection amplitude results in an increase of plate stiffness, and therefore causes an increase in the natural frequencies.

Fig. 4 shows the load ratio (i.e. $P / P_{c r}$ ) in terms of the transverse displacement of the center point of specified plate. The results show the excellent accuracy of the proposed method as compared with the FEM. It should be noted that the solution of the nonlinear problems, unlike the linear ones, only satisfies the boundary conditions and guarantees the energy conservation law [17]. Hence, the full compliance of responses in such an analysis seems unlikely.

Fig. 5 shows the effect of initial imperfection amplitudes on the buckling behavior of the plate. An increase in the imperfection amplitude has a considerable impact on the behavior of the plate in vicinity of critical load. Therefore, an increase of the imperfection amplitude changes the plate buckling behavior. For example, at $W_{0} / h =$ 1, the critical load is indistinguishable. A decrease of the imperfection amplitude will make the buckling behavior more visible, and the results become closer to the results of a flat plate. On the other hand, it can be seen that, if the axial load increases, the effects of geometrical imperfection will decrease. As a result of this, for deflections larger than 1.5 times of the thickness, the corresponding curves are coincided. Since the imperfection is negligible as compared with the plate deflections, its effect disappears and leads to the convergence of the diagrams. It can be concluded that with the existence of imperfection, it is inevitable to use the nonlinear analysis in order to obtain the buckling load of plate.

Fig. 3Variations of natural frequencies against initial imperfection amplitude ratio

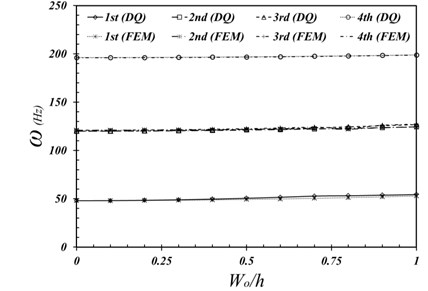
Fig. 4Comparison of load-deflection curves as given by DQ (…) and FEM (---)

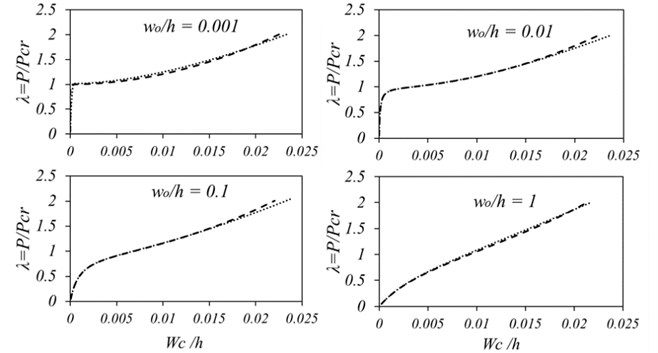
Fig. 5Load-deflection curves of SSSS square plate for different amount of initial imperfection amplitude

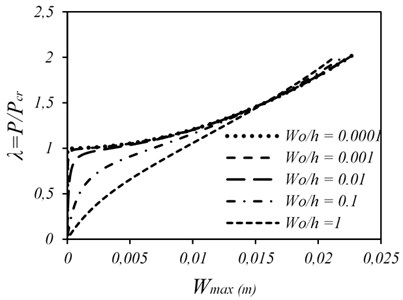
Fig. 6first five frequencies of SSSS plate (wo/h= 0.1)

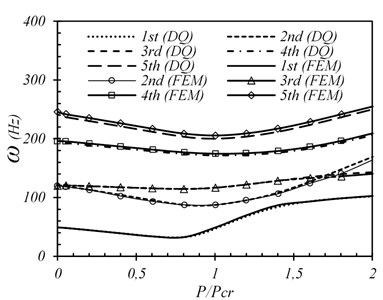
The variations of the first five natural frequencies of a simply supported plate with different amounts of initial imperfections in the state of the pre- and post-buckling vibration are presented in Figs. 6-8. It can be seen that as far as the applied compressive load increases from zero to the buckling load ( $P / P_{c r} <$ 1), all the frequencies decrease smoothly due to a reduction in the plate stiffness. A load increase to buckling load and beyond causes an increase in the frequencies ( $P / P_{c r} >$ 1). It can also be concluded that the lowest natural frequencies of the structure occur at the buckling load ( $P / P_{c r} =$ 1). Natural frequencies decrease due to a reduction in the plate stiffness before the critical load and then increase as a consequence of a rise in the plate deformation which causes an increase in the plate stiffness by dominating the stretching stiffness over the bending stiffness.

Fig. 9 shows the first five mode shapes of a simply supported square plate, before and after buckling. In this figure, the pre- and post-buckling loads are 0.5 and 1.5 times the critical load, respectively. Looking at Fig. 9, one can conclude that the first and second mode shapes have more variations as compared with the other modes. This is also shown in Figs. 6-8.

Fig. 7First five frequencies of SSSS plate (wo/h= 0.01)

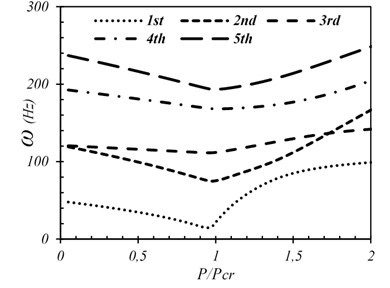
Fig. 8First five frequencies of SSSS plate (wo/h= 0.001)

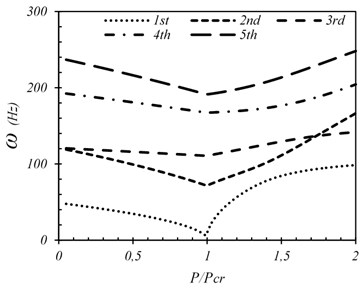
Fig. 9First five mode shape of SSSS Square plate at pre-buckling (P/Pcr= 0.5) and post-buckling state (P/Pcr= 1.5)

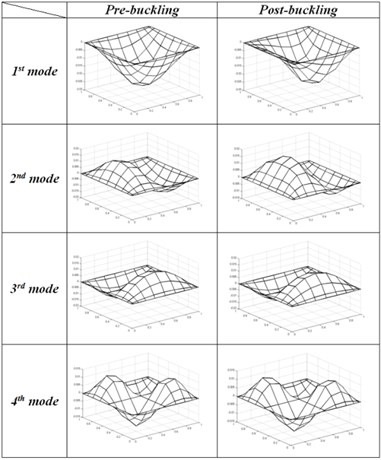
Fig. 10 shows the variation of the first four natural frequencies of the aforementioned plate with different initial imperfection amplitudes against the compressive load. It can be seen that the first two frequencies are more sensitive with respect to changes in the initial imperfection amplitudes than the last two ones. However, as the compressive in-plane load increases from the buckling load, the effect of imperfection amplitude decreases. This is due to the fact that after buckling, the plate curvature increases and the initial imperfection becomes negligible as compared with it.

The solution for the other boundary conditions can also be calculated using the same method. Frequencies and mode shapes for different combinations of simply supported and clamped boundary conditions are provided in Figs. 11-14.

Fig. 10Variations of first four natural frequencies of SSSS plate with load ratio, wo/h= 0.001 (_), wo/h= 0.01 (…) and wo/h= 0.1 (---)

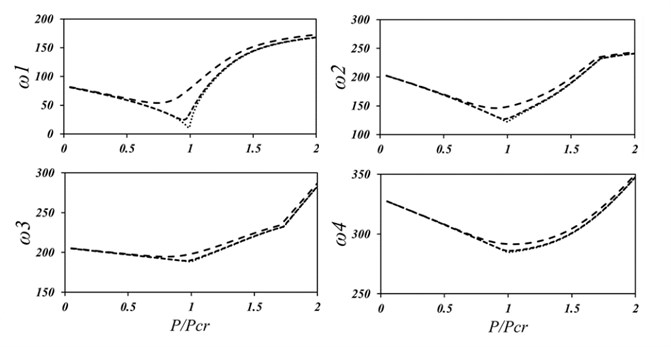
Fig. 11First five frequencies of fully clamped plate (wo/h= 0.01)

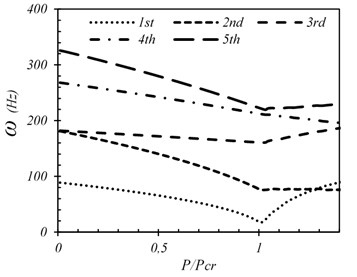
Fig. 11 presents the variations of the first five natural frequencies of a fully clamped square plate under uniaxial compressive loads. The figure shows that an increase of the applied compressive load from zero toward the buckling load results in a smooth reduction in all the natural frequencies. After the buckling, due to an increase in the stretching stiffness of the plate, the curves for the odd frequencies also start increasing. However, the even natural frequencies continue decreasing after the buckling. Besides, the figure also shows that after the buckling, the fundamental natural frequency increases with the applied load increase and exceeds the second frequency. The first mode shape of the plate is the first symmetric bending-stretching mode, whereas the second mode is the bending mode shape. Fig. 12 shows mode shapes of a fully clamped plate before and after the intersection.

Fig. 12first five mode shape of CCCC Square plate at pre-buckling (P/Pcr= 0.5) and post-buckling state (P/Pcr= 1.4)

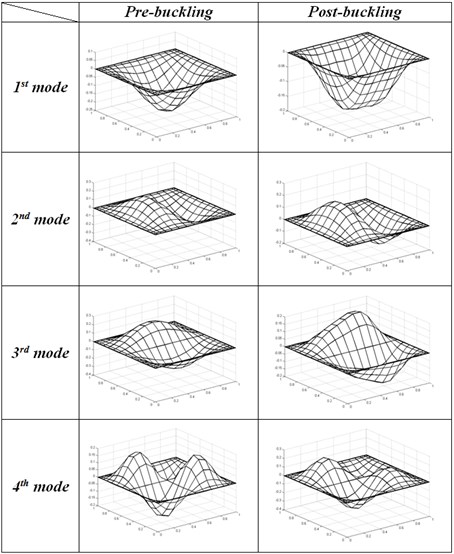
Fig. 13First five frequencies of CSCS plate (wo/h= 0.01)

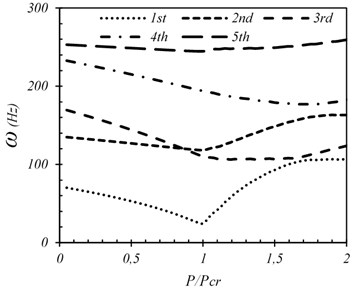
Fig. 14First five frequencies of SCSC plate (wo/h= 0.01)

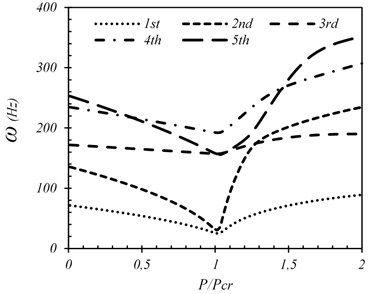
Fig. 13 illustrates the variations of natural frequencies of an imperfect square plate with imperfection amplitude of 0.01 h, where all the loaded edges are clamped, and the rest ones are simply supported. The figure shows that all the frequencies decrease as the load factor increases. However, as the load continues increasing after buckling, the first, second, third and fifth frequencies increase due to the dominance of the stretching stiffness over the bending stiffness, while the forth frequency still decreases because it has a bending mode. It can be seen that at a load of 0.848 $P_{c r}$ , the second and the third frequencies intersect. After the intersection, the second frequency continues increasing its distance as compared with the third frequency.

Fig. 14 demonstrates the variations of the natural frequencies of a plate with two simply supported loaded edges and two clamped edges having imperfection amplitude equal to 0.01 h. with the increase of the applied compressive load up to the buckling load, all of the natural frequencies decrease smoothly. But, as far as the applied load increases from this point, due to the stretching stiffness, an increase in all frequencies takes place at once. Furthermore, at load ratios of 0.418, 1.281 and 1.444, there are intersections between the fourth and fifth, the second and third and again, the fourth and the fifth frequencies, respectively.

7. Conclusions

In this study, the effects of initial geometric imperfection and pre- and post-buckling deformations on natural frequencies of plates under uniaxial in-plane loads were investigated. The solution of the nonlinear differential equations consists of static and dynamic parts. The differential quadrature method together with an arc-length strategy was used to solve the static part, while the dynamic part was linearized and then solved using the differential quadrature method. The effects of initial imperfection and plate deformation on frequencies and mode shapes were examined for four different combinations of clamped and simply supported boundary conditions. The accuracy and the integrity of results were investigated using results obtained from a commercial software package for the finite element methods.

It was observed that in a fully simply supported plate, with the increase of the initial imperfection, the natural frequencies also increase. However, an increase in the in-plane compressive load before the buckling load generally reduces the natural frequencies and afterwards increases them. The increase in natural frequencies for some modes results in their intersection. Furthermore, the investigation shows that the frequencies are sensitive to the imperfection amplitudes, especially about the buckling load. The similar behaviors with some differences could be seen for other combinations of the boundary conditions. It could be concluded that the effects of initial imperfection and in-plane compressive loads before and after the buckling are highly dependent on the boundary conditions. The research also shows that prior to buckling, an increase in the applied compressive load results in a smooth decrement of all natural frequencies for a SSSS plate, with no intersections between the modal shapes. However, for SCSC and CSCS plates the same conclusion can be drawn except that there are some intersections between natural frequencies. The mode intersections happen more frequently after the buckling for all the boundary conditions.

References

Hui D., Leissa A. W. Effects of geometric imperfections on vibrations of biaxially compressed rectangular flat plates. Transactions of the ASME, Vol. 50, 1983, p. 750-756.

Publisher
Ilanko S., Dickinson S. M. The vibration and post-buckling of geometrically imperfect, simply supported, rectangular plates under uni-axial loading, Part I: Theoretical approach. Journal of Sound and Vibration, Vol. 118, Issue 2, 1987, p. 313-336.

Publisher
Ilanko S. Vibration and post-buckling of in-plane loaded rectangular plates using a multiterm Galerkin’s method. Journal of Applied Mechanics, Vol. 69, 2002, p. 589-592.

Publisher
Ng C. F., White R. G. Dynamic behavior of postbuckled isotropic plates under in-plane compression. Journal of Sound and Vibration, Vol. 120, Issues 1-8, 1988, p. 1-18.

Publisher
Pasic H., Herrmann G. Non-linear free vibration of buckled plates with deformable loaded edges. Journal of Sound and Vibration, Vol. 87, Issues 1-8, 1983, p. 105-114.

Publisher
Sassi S., Ostigu G. L. Analysis of the variation of frequencies for imperfect rectangular plates. Journal of sound and vibration, Vol. 177, Issue 5, 1994, p. 675-687.

Publisher
Williams M., Griffin B., Homeijer B., Sankar B., Sheplak M. Vibration of post-buckled homogeneous circular plates. IEEE Ultrasonics Symposium, 2007.

Publisher
Girish J., Ramchandra L. S. Thermal postbuckled vibrations of symmetrically laminated composite plates with initial geometric imperfections. Journal of Sound and Vibration, Vol. 282, 2005, p. 1137-1153.

Publisher
Li S. R., Batra R. C., Ma L. S. Vibration of thermally post-buckled orthotropic circular plates. Journal of Thermal Stresses, Vol. 30, 2007, p. 43-57.

Publisher
Panda S. K., Singh B. N. Nonlinear free vibration of spherical shell panel using higher order shear deformation theory – a finite element approach. International Journal of Pressure Vessels and Piping, Vol. 86, 2009, p. 373-383.

Publisher
Panda S. K., Singh B. N. Thermal post-buckling behaviour of laminated composite cylindrical/hyperboloidal shallow shell panel using nonlinear finite element method. Composite Structures, Vol. 91, 2009, p. 366-374.

Publisher
Bellman R. E., Kashef B., Casti J. Differential quadrature: a technique for the rapid solution of nonlinear partial differential equation. Journal of Computer Physics, Vol. 1, 1971, p. 133-143.

Publisher
Quan J. R., Chang C. T. New insights in solving distributed system of equations by quadrature-method. Journal of Compute Chemistry Engineering, Vol. 13, 1989, p. 1017-1024.

Publisher
Wempner G. A. Discrete approximation related to nonlinear theories of solids. International Journal of Solids and Structures, Vol. 7, 1971, p. 1581-1599.

Publisher
Riks E. The application of Newton’s method to the problem of elastic stability. Journal of Applied Mechanics, Vol. 39, 1972, p. 1060-1065.

Publisher
Forde B. D. R., Stiemer S. F. Improved arc length orthogonality methods for nonlinear finite element analysis. Computers and Structures, Vol. 27, 1987, p. 625-630.

Publisher
Chia C. Y. Nonlinear Analysis of Plates. McGraw-Hill, New York, 1980.

Search CrossRef

Cited by

Effect of crack characteristics on the vibration behavior of post-buckled functionally graded plates

Emadaldin Sh Khoram-Nejad | Shapour Moradi | Mohammad Shishehsaz

(2023)

A novel compliant assembly variation analysis with consideration of initial deviation and welding shrinkage

(2021)

About this article

Received

14 February 2017

Accepted

12 August 2017

Published

15 February 2018

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/jve.2017.18252

Keywords

post-buckling

vibration

imperfection

shear deformation

differential quadrature

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2019 11 28

Comparative study for modal analysis of circular plates with various cutouts and end conditions

Vedanth Bhatnagar, Pavan Kishore Mamaduri, Sreenivasulu B

Research article

2018 08 15

Free longitudinal vibrations of functionally graded tapered axial bars by pseudospectral method

Sri Harikrishna Pillutla, Sudheer Gopinathan, Vasudeva Rao Yerikalapudy

Research article

2017 09 30

Shooting method for free vibration of FGM Reissner-Mindlin circular plates resting on elastic foundation in thermal environments

Qing-Lu Li, Wei-Di Luan, Zuo-Quan Zhu

Research article

2016 12 31

Vibration and post-buckling of a functionally graded beam subjected to non-conservative forces

Qing Lu Li, Jing Hua Zhang

H. Makvandi, S. Moradi, D. Poorveis, and K. Heidari Shirazi, “Differential quadrature method (DQM) for studying initial imperfection effects and pre- and post-buckling vibration of plates,” Journal of Vibroengineering, Vol. 20, No. 1, pp. 103–115, Feb. 2018, https://doi.org/10.21595/jve.2017.18252

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2017.18252
UR  - https://doi.org/10.21595/jve.2017.18252
TI  - Differential quadrature method (DQM) for studying initial imperfection effects and pre- and post-buckling vibration of plates
T2  - Journal of Vibroengineering
AU  - Moradi, Shapour
AU  - Makvandi, Hesam
AU  - Poorveis, Davood
AU  - Heidari Shirazi, Kourosh
PY  - 2018
DA  - 2018/02/15
PB  - JVE International Ltd.
SP  - 103-115
IS  - 1
VL  - 20
SN  - 1392-8716
ER  - 

Copy Ris

Copied to clipboard!

@article{Moradi_2018,
	doi = {10.21595/jve.2017.18252},
	url = {https://doi.org/10.21595/jve.2017.18252},
	year = 2018,
	month = {feb},
	publisher = {{JVE} International Ltd.},
	volume = {20},
	number = {1},
	pages = {103--115},
	author = {Shapour Moradi and Hesam Makvandi and Davood Poorveis and Kourosh Heidari Shirazi},
	title = {Differential quadrature method ({DQM}) for studying initial imperfection effects and pre- and post-buckling vibration of plates},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]S. Moradi, H. Makvandi, D. Poorveis, and K. Heidari Shirazi, “Differential quadrature method (DQM) for studying initial imperfection effects and pre- and post-buckling vibration of plates,” Journal of Vibroengineering, vol. 20, no. 1, pp. 103–115, Feb. 2018, doi: 10.21595/jve.2017.18252.

Copy IEEE

Copied to clipboard!

Moradi, Shapour, Hesam Makvandi, Davood Poorveis, and Kourosh Heidari Shirazi. “Differential Quadrature Method (DQM) for Studying Initial Imperfection Effects and Pre- and Post-Buckling Vibration of Plates.” Journal of Vibroengineering 20, no. 1 (February 15, 2018): 103–15. https://doi.org/10.21595/jve.2017.18252.

Copy Chicago

Copied to clipboard!

Differential quadrature method (DQM) for studying initial imperfection effects and pre- and post-buckling vibration of plates

Abstract

1. Introduction

2. Governing equations

3. Initial imperfection

4. Post-buckling

5. Pre- and post-buckling vibration

6. Results

7. Conclusions

References

Cited by

About this article

Related Articles