Vibration and post-buckling of a functionally graded beam subjected to non-conservative forces

1. Introduction

Follower forces are non-conservative whose lines of action are affected by the deformation of the elastic system on which they act. Bolotin [1] analyzed the stability of a clamped-free rod subjected to a concentrated compressing follower force at the free end, named Beck’s problem. Leipholz [2] studied infinitesimal stability of elastic beams subjected to uniformly and linearly continuously distributed, tangential follower forces. By using finite element method, Vitaliani et al. [3] and Detinko [4] investigated the stability problem of cantilever beams and semi-circle arches with large elastic deformations under end tip follower load, the load-displacement diagram and load-square of frequency curves were present. Based on the theory of accuratly axial extension beam, Li and Zhou [5] studied the post-buckling behaviors of a homogenous beam with hinged-fixed ends under uniformly distributed tangential follower forces.

The concept of functionally gradient materials (FGM) was first introduced in 1984 by a group of materials scientists in Japan [6, 7]. FGM are both macroscopically and microscopically heterogeneous composites which are normally made from a mixture of ceramics and metals with continuous composition gradation from pure ceramic on one surface to full metal on the other. This leads to gradual and smooth change in the material profile as well as the effective material properties, making them distinguish from the conventional fiber-matrix composites and preferable in many fields of engineering applications. So, the studies of the mechanical behaviors of FGM structures under the mechanical and thermal loadings have being attracted more and more attentions of scientists and also have become a new research field of solid mechanics. Xiang and Yang [8] studied both free and forced vibrations of an FGM beam with variable thickness under thermally induced initial stresses based on the Timoshenko beam theory. Reddy and Chin[9] investigated the dynamic thermo-elastic response of functionally graded cylinders and plates. Li et al. [10] studied the thermal post-buckling of FGM Timoshenko beams with material properties changing continuously in the thickness direction by a power law function. Li et al. [11] further examined free vibration of FGM beams with surface-bonded piezoelectric layers in thermal environment. Employing the finite element method, Bhangale and Ganesan [12] carried out thermo-elastic buckling and vibration analysis of a sandwich beam made from FGM. Ying et al. [13]presented solutions for bending and free vibration of FGM beams resting on a Winkler-Pasternak elastic foundation. Aydogdu and Taskin [14] investigated the free vibration behavior of a simply supported FGM beam based on the theory of classical beam. Yang and Chen [15] studied the free vibration and elastic buckling of FGM beams with open edge cracks by using classical beam theory. The authors [16] of this paper carried out free vibration of FGM Euler-Bernoulli beams with post-buckling configuration subjected to axial force and presented characteristics curves of the first three lower frequencies versus the load parameters. Zhang and Zhou [17] defined a physical neutral surface that is different from the geometric mid-surface of a plate and studied the bending, vibration and nonlinear bending behaviors of FGM doubly curved shallow shin shell. Ma and Lee [18] derived governing equations for both the static behavior and dynamic response of FGM beams on the physical neutral surface. Ramesh and Mohan Rao [19] discussed the natural frequencies of vibration of a rotating pre-twisted functionally graded cantilever beam. Ghiasian et al. [20] studied the static and dynamic buckling of an FGM beam subjected to uniform temperature rise loading and uniform compression. Recently, Li et al. [21] studied the free vibration of FGM beams based on both the classical and first-order shear deformation beam theories. Recently, Zhang et al. [22] present the thermal shock responses of cylindrical shell by differential quadrature solutions.

To the author’s knowledge, fewer researchers have given much attention to the static behaviors of FGM beams subjected to non-conservative forces. Especially, the dynamic response of buckled FGM beams due to follower loadings has not been appeared. Therefore, the present paper focus on the harmonic responses of vibrations of post-buckled FGM beams under distributed tangential follower force. We consider an FGM elastic beam with one end hinged and the other fixed, subjected to a uniformly distributed tangentially compressing follower forces. First, the dynamic governing equations of this problem are established on the basis of the geometrically nonlinear theory for axially extensible beams. By assuming that the amplitude of the vibrated beam is small and its response is harmonic, the above mentioned nonlinear partial differential equations are reduced to two sets of coupled ordinary differential equations. One is for the static post-buckling deformation and the other is for the linear vibration in post-buckling configurations. Finally, by using the shooting method in conjunction with an analytical continuation, the post-buckling configurations as well as the linear responses of the pre-buckling and post-buckling FGM beam are obtained. The equilibrium paths as well as the post-buckling configurations of the deformed FGM beam are plotted. The characteristic relationships between frequencies and load parameter are presented numerically. The material properties are assumed to vary continuously through the thickness of the beam. Effects of material properties on the post-buckling behavior and vibration of the FGM beam are discussed in detail.

2. Basic equations

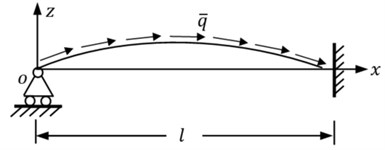
Consider a beam made from functionally graded material, with initial length $l$ and rectangular cross-section of width $b$ and height $h$, subjected to a distributed non-conservative force $\stackrel{-}{q}$ along the axis of the beam as shown in Fig. 1. Take $x$-coordinate along the axial line of the beam, $z$-coordinate along the thickness. According to Leipholz’s point of view [2], divergence type systems, which are fairly frequent in practice, can be treated by disregarding damping.

Fig. 1A hinged-fixed functionally graded material beam subjected to uniformly distributed follower force

2.1. Material properties of FGM

It is assumed that the material properties (such as the Young’s modulus, $E$, mass density, $\rho$) of the beam vary along the height of the beam and obey the following relation [9]:

1

$P=P_c{V}_c+P_m（1-V_c）,$

where the subscripts $c$ and $m$ denote the ceramic and metallic constituents, respectively, $V_c$ denotes the volume fraction of ceramic and follows a simple power low as:

2

$V_c={\left(\frac{1}{2}+\frac{z}{h}\right)}^n,$

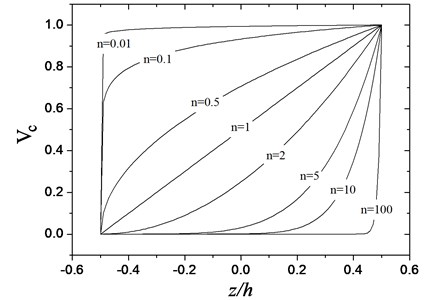
where $n$ is the gradient index of FGM. According to this distribution, the bottom surface of the functionally graded beam is pure metal and the top surface is pure ceramic, and for different values of $n$ one can obtain different volume fractions of ceramics. Fig. 2 shows the variations of volume fraction of ceramic constituent through the thickness of beam for various values of $n$ calculated from Eq. (2). Generally, Poisson’s ratio $v$ varies in a small range. For simplicity, we assume $v$ be a constant for functionally graded materials. The effective Young’s modulus $E\left(z\right)$ and mass density $\rho \left(z\right)$ of the FGM beam follow the distribution law of Eqs. (1) and (2), namely:

3

$E\left(z\right)=E_c{\left(\frac{1}{2}+\frac{z}{h}\right)}^n+E_m\left[1-{\left(\frac{1}{2}+\frac{z}{h}\right)}^n\right],$

4

$\rho \left(z\right)={\rho }_c{\left(\frac{1}{2}+\frac{z}{h}\right)}^n+{\rho }_m\left[1-{\left(\frac{1}{2}+\frac{z}{h}\right)}^n\right],$

where $E_c$ and $E_m$ are elastic modulus of ceramic and metal, ${\rho }_c$ and ${\rho }_m$ are mass density of ceramic and metal respectively.

Fig. 2Variations of the volume fraction of ceramic versus the dimensionless thickness of the functionally grated material beam for different values of n

On the assumption that the cross-section remains plane during deforming, one can get the strain at an arbitrary point in the cross-section:

5

$\epsilon \left(x,z\right)=R-1-\frac{d\theta }{dx}z.$

The stress-strain relation of FGM beam is:

6

$\sigma \left(x,z\right)=E\left(z\right)\epsilon \left(x,z\right).$

Axis force $N\left(x\right)$ and bending moment $M\left(x\right)$ are:

7

$N\left(x\right)={\iint }_A\sigma dA={\iint }_{A}E\left(z\right)\left(R-1-\frac{d\theta }{dx}z\right)dA=A_1\left(R-1\right)-B_1\frac{d\theta }{dx},$

8

$M\left(x\right)={\iint }_A\sigma zdA={\iint }_{A}E\left(z\right)z\left(R-1-\frac{d\theta }{dx}z\right)dA=-B_1\left(R-1\right)+D_1\frac{d\theta }{dx},$

in which $A_1=bh{E}_c{F}_1/2$, $B_1=b{h}^2{E}_c{F}_2/4$, $D_1=b{h}^3{E}_c{F}_3/8$, $F_1$, $F_2$ and $F_3$ are the resultant stiffness coefficients calculated by:

$F_1={\int }_{-1}^1{f}_E(\eta ,n,r_E)d\eta ,F_2={\int }_{-1}^1{f}_E(\eta ,n,r_E)\eta d\eta ,F_3={\int }_{-1}^1{f}_E(\eta ,n,r_E){\eta }^{2}d\eta ,$
$f_E\left(\eta ,n,r_E\right)={\left(\frac{1+\eta }{2}\right)}^n+r_E\left[1-{\left(\frac{1+\eta }{2}\right)}^n\right],r_E=\frac{E_m}{E_c},\eta =\frac{2z}{h}.$

The axial force in the cross section also can be expressed as:

9

$N\left(x\right)=-H\mathrm{c}\mathrm{o}\mathrm{s}\theta -V\mathrm{s}\mathrm{i}\mathrm{n}\theta ,$

where $H$ and $V$ are the internal resultant forces in the longitudinal and transverse directions, respectively.

Substituting Eq. (6) into Eqs. (7)-(8), obtains:

10

$\frac{d\theta }{dx}=\frac{1}{(F_2^2-F_1{F}_3)E_{c}I}\left[\frac{1}{3}{F}_{2}h\left(H\mathrm{c}\mathrm{o}\mathrm{s}\theta +V\mathrm{s}\mathrm{i}\mathrm{n}\theta \right)-\frac{2}{3}{F}_{1}M\right],$

11

$R=\frac{1}{(F_2^2-F_1{F}_3)E_{c}I}\left[\frac{1}{6}{F}_3{h}^2\left(H\mathrm{c}\mathrm{o}\mathrm{s}\theta +V\mathrm{s}\mathrm{i}\mathrm{n}\theta \right)-\frac{h}{3}{F}_{2}M\right]+1,$

where $I=b{h}^3/12$.

3. Solutions to the problem

To analyze the free vibration of the FGM beam in the vicinity of static pre-buckling and post-buckling equilibrium states, we seek solutions of Eq. (16) of the following form:

where $U_s\left(X\right)\text{,}$$W_s\left(X\right)\text{,}$${\theta }_s\left(X\right)\text{,}$$H_s\left(X\right)\text{,}$$V_s\left(X\right)\text{,}$$M_s\left(X\right)$ indicate the solution of statically post-buckling of the beam, $U_d(X,\tau )$, $W_d(X,\tau )$, ${\theta }_d(X,\tau )$, $H_d(X,\tau )$, $V_d(X,\tau )$, $M_d(X,\tau )$ indicate the dynamic responses near the nonlinear static configuration for the FGM beam.

3.1. Post-buckling solutions

The governing equations of the nonlinear static problem of the FGM beam under a compressing follower loading can be obtained from Eq. (18) by neglecting the inertial terms, which are as follows:

19

$\frac{d{U}_s}{dX}=R_s\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_s-1,$
$\frac{d{W}_s}{dX}=R_s\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_s,$
$\frac{d{\theta }_s}{dX}=\frac{1}{F_2^2-F_1{F}_3}\left[\frac{F_2}{3\delta }\left(H_s\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_s+V_s\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_s\right)-\frac{2F_1}{3}{M}_s\right],$
$\frac{d{H}_s}{dX}=R_{s}q\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_s,$
$\frac{d{V}_s}{dX}=R_{s}q\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_s,$
$\frac{d{M}_s}{dX}=R_s\left(-H_s\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_s+V_s\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_s\right),$
$R=1+\frac{1}{F_2^2-F_1{F}_3}\left[\frac{F_3}{6{\delta }^2}\left(H_s\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_s+V_s\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_s\right)-\frac{F_2}{3\delta }{M}_s\right].$

The boundary conditions of the FGM beam corresponding to the post-buckling, in dimensionless form, are shown in Fig. 1 can be expressed as:

20

$W_s=H_s=M_s=0,\mathrm{}\mathrm{}\mathrm{}\mathrm{}{\theta }_s=\beta ,\mathrm{a}\mathrm{t}X=0,$
$U_s=W_s={\theta }_s=0,\mathrm{}\mathrm{}\mathrm{}\mathrm{a}\mathrm{t}\mathrm{}\mathrm{}\mathrm{}X=1.\mathrm{}$

The last one of Eqs. (20a) is a normalized condition prescribed for the beam, and $\beta$ is the rotational angle of the cross-section of the left end.

Due to the strong non-linearity and the coupling including in Eq. (19), it is very difficult to obtain any analytical solution of this problem. Herein, a shooting method is employed to numerically solve the problem. First, we transform the two-point boundary value problem into an initial value problem with some unknown initial parameters. Then, the unknown parameters are estimated to start computations by the fourth order Runge-Kutta method, and these estimates are modified by the Newton-Raphson method until specified boundary conditions at the terminal point are satisfied. The details about this numerical approach can be found in the literatures, such as works by Li and Zhou [23]; William et al. [24]; Ma and Wang [25].

Based on the bifurcation theory, the minimum eigenvalue of the linearized problem $(\beta \to 0)$ of the nonlinear boundary value problem is the critical load of the beam instability, denoted by $q_{cr}$. When $q<q_{cr}$ the initial equilibrium of the beam is stable, when $q>q_{cr}$, the beams go into post-buckled state.

In what follows, a ceramic (zirconia) and metal (Ti-6AI-4V) system of FGM is considered. The material parameters, Young’s modulus, Poisson’s ratio and mass density are taken from the Ref. [25] which are summarized in Table 1.

Table 1Material parameters of ceramic, zirconia and metal Ti-6AL-4V in the FGM system

Materials	Young’s modulus $E$ (GPa)	Poission’s ratio $v$	Mass density ${\rho }_0$ (kg/m)
Zirconia	244.27	0.3	4429
Ti-6AL-4V	122.56	0.3	3000

In the following numerical computation for the post-buckling deformation of the FGM beam, we prescribe the slenderness $\delta =$ 30. For some specific values of $\beta$, post-buckling equilibrium configurations are presented. The post-buckling equilibrium paths of the FGM beam with different values of $(\beta ,q)$ are calculated and plotted in Fig. 3, in which the gradient index of FGM beam is $n=$ 0.5.

Fig. 3Equilibrium configurations of the hinged-fixed beam with some prescribed values of β under follower force (n=0.5)

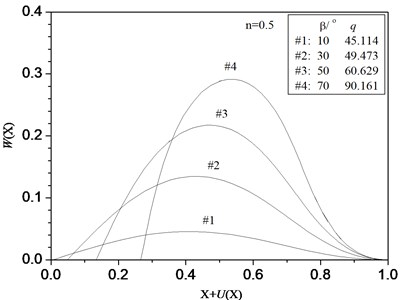
Fig. 4Characteristic curves of β vs. load q of the hinged-fixed FGM beam with different values of n

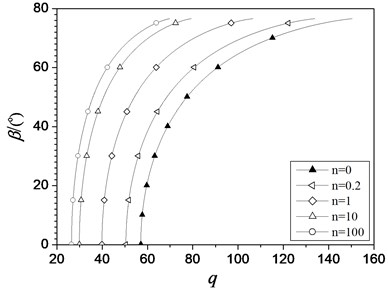
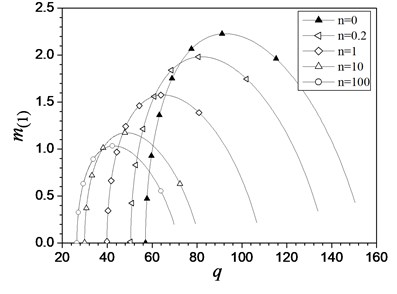
The typical post-buckling paths of hinged-fixed FGM beams are shown in Figs. 4-6. Fig. 4 and Fig. 5 show the rotational angle and left end displacement vs. load parameter $q$ for different values of material constant $n$, respectively. Fig. 6 show right end bending moment vs. load parameter $q$ for different values of material constant $n$. The post-buckling behaviors of ceramic beam are in excrement agreement with those of homogenous beam [5]. It is clear that the deflection of the FGM beam is higher than that of pure ceramic beam (i.e. $n=0$). It also can be seen that the load-deformation behaviors of FGM beam are similar than those of homogenous beams. The coordinates of intersection points of the curves with $q$-axis give the dimensionless critical buckling load parameters $q_{cr}$. It is clear that the critical buckling load decreases with the increase of the value of $n$. This is because pure ceramic beam has higher stiffness than the functionally graded beam.

Fig. 5Characteristic curves of U(0) vs. load q of the hinged-fixed FGM beam with different values of n

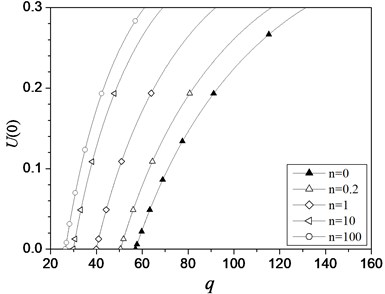
Fig. 6Characteristic curves of m(1) vs. load q of the hinged-fixed FGM beam with different values of n

3.3. Harmonic responses of the linear vibrations

We find the solution in synchronous of terms as:

22

$\left(U_d,W_d,{\theta }_d,H_d,V_d,M_d\right)=\left(u_d,w_d,{\mathrm{\Theta }}_d,h_d,v_d,m_d\right)\mathrm{c}\mathrm{o}\mathrm{s}\omega \tau ,$

where $\omega$ is the natural frequency of the beam system, and $u_d$, $w_d$, ${\mathrm{\Theta }}_d$, $h_d$, $v_d$, $m_d$ are shape functions. The substitution of Eq. (21) into Eq. (16) and (19) achieve the ordinary differential equations for the amplitude functions as:

23

$\frac{d{h}_d}{dX}=R_s\left[{\omega }^2{u}_d-q{\mathrm{\Theta }}_d\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_s\right]+\mathrm{\Gamma }q\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_s,$
$\frac{d{v}_d}{dX}=R_s\left[{\omega }^2{w}_d+q{\mathrm{\Theta }}_d\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_s\right]+\mathrm{\Gamma }q\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_s,$
$\frac{d{u}_d}{dX}=-R_s{\mathrm{\Theta }}_d\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_s+\mathrm{\Gamma }\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_s,$
$\frac{d{w}_d}{dX}=R_s{\mathrm{\Theta }}_d\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_s+\mathrm{\Gamma }\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_s,$
$\frac{d{\Theta }_d}{dX}=\frac{1}{F_2^2-F_1{F}_3}\left\{\frac{F_2}{3\delta }\left[(h_d+V_s{\mathrm{\Theta }}_d)\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_s+(v_d-H_s{\mathrm{\Theta }}_d)\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_s\right]-\frac{2F_1}{3}{m}_d\right\},$
$\frac{d{m}_d}{dX}=R_s\left[-(h_d+V_s{\mathrm{\Theta }}_d)\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_s+(v_d-H_s{\mathrm{\Theta }}_d)\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_s\right]$
$\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}-\frac{F_5}{4F_4{\delta }^2}{\omega }^2{\mathrm{\Theta }}_d+\mathrm{\Gamma }\left(V_s\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_s-H_s\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_s\right),$

where:

24

$\mathrm{\Gamma }=\frac{\left\{\frac{F_3}{6{\delta }^2}\left[\left(H_s{\mathrm{\Theta }}_d-v_d\right)\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_s-F_3\left(V_s{\mathrm{\Theta }}_d+h_d\right)\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_s\right]+\frac{F_2}{3\delta }{m}_d\right\}}{F_1{F}_3-F_2^2}.$

For the beam with hinged-fixed ends, the boundary conditions corresponding to vibration problem are as follows:

25

$w_d=h_d=m_d=0,\mathrm{}\mathrm{}\mathrm{}\mathrm{a}\mathrm{t}\mathrm{}\mathrm{}X=0,$
$u_d=w_d={\theta }_d=0,\mathrm{}\mathrm{}\mathrm{}\mathrm{a}\mathrm{t}\mathrm{}\mathrm{}X=1.$

If the beam is not buckled, that is $U_s=W_s={\theta }_s=V_s=M_s=0$, then Eqs. (22)-(25) govern the linear vibrations of pre-buckled beam.

3.3.1. Numerical simulation and discussions

Here, we also use the shooting method to seek for the numerical solutions to this problem, and specify the geometric parameter $\lambda =$ 150. The two boundary value problems are solved simultaneously in the numerical computation, in order to ensure the same discrete points for both the post-buckling solution and the vibration ones are the same in the numerical integration of the fourth-order Runge-Kutta method.

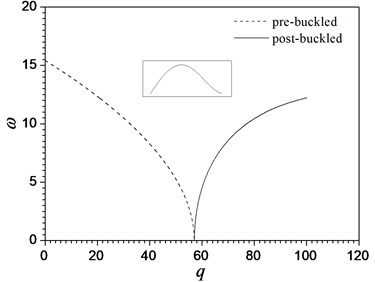
In the special case that the beam is homogenous $(n=$ 0$)$pure ceramic beam, the first divergence load parameter obtained in this paper is 57.07, which is very close to the accurate solution [3, 5]. Fig. 7 shows the relation curves between the non-conservative load parameters and non-dimensional frequency for different vibration modes.

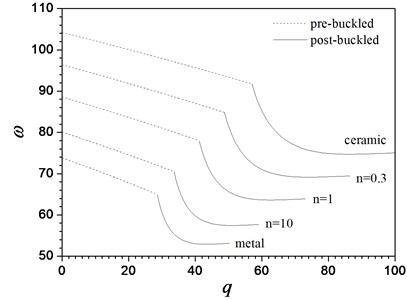
Figs. 8 shows the characteristic curves of the first three order dimensionless natural frequencies versus the dimensionless load parameter of the FGM beam with different values of the material constant $n$ in pre-buckling (dashed lines) and post-buckling (solid lines) states. As it usually appears, the first-order frequency becomes zero when $q=q_{cr}$. The results in Figs. 7 show that a beam with a specified value of $n$ in an unbuckled state, the first three frequencies decease with the increase of the load parameters. This decrease in frequencies with loading is attributed to the fact that the loading induced compressive stress weakens the beam stiffness. In the post-buckling domain, the first and second order frequencies increasing with the increasing $q$, but the third-order frequencies decrease with the increasing $q$. However, as the post-buckling deformation become more significant, the frequencies seem to tend to a constant. As expected, the fundamental frequencies approach zero at the buckling points. The material constant $n$ has obvious effects on the frequencies. With the increase in the value of $n$, the frequencies decrease in the pre-buckling states but increase in the post-buckling states except for the third-order frequencies of the FGM beam. We also find that the load-frequency curves are continuous but not smooth at the point of the critical load $q_{cr}$. Li et al. [26] reveal that this is because a bifurcation points of the corresponding equilibrium paths over which the beam goes into its secondary equilibrium state, i.e. post-buckling state.

Fig. 7Variations of the first three frequencies ω near the nonlinear buckled configuration with load parameters q for a homogeneous ceramics beam

a) The fundamental frequency

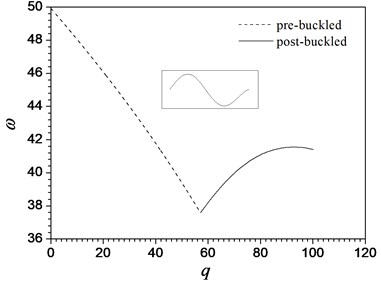
b) The second-mode frequency

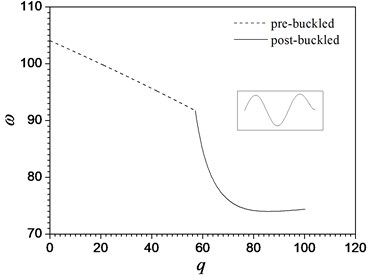
c) The third-mode frequency

4. Conclusions

The post-buckling and small free vibration in the vicinity of the post-buckling configurations of hinged-fixed FGM beam subjected to distributed non-conservative forces were investigated. Based on the geometrically nonlinear theory considering the extensibility of the FGM beam, governing equations for the problem were derived, and then a shooting method technique is employed to numerically solve the nonlinear equations. The deformed configuration, post-buckling equilibrium paths and characteristic curves of the lower order frequencies during pre-buckling and post-buckling vs. the load parameters were presented. Effects of material constant $n$on the critical buckling loading, the post-buckling behaviors and the frequencies of the FGM beam were discussed in detail. The following conclusions are arrived from present study.

Fig. 8Variation of the first three frequenciesω near the nonlinear buckled configuration with load parameters q for a hinged-fixed FGM beam for different values of material constant n

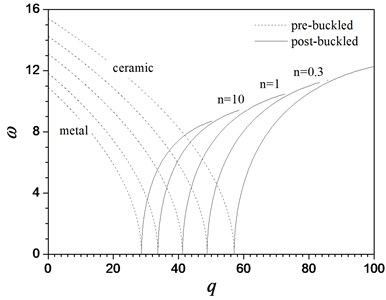
a) The fundamental frequency

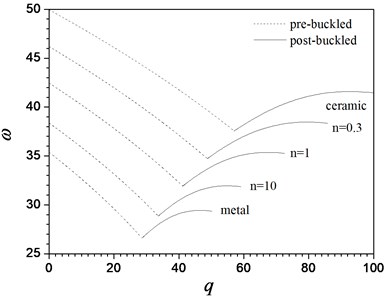
b) The second-mode frequency

c) The third-mode frequency

1. Post-buckling behaviors of FGM beam exhibit bifurcations under follower force. The critical buckling load decreases and the post-buckling deflection increases with increasing the volume of $n$, it is due to the increase of the volume fraction of the metal reduces the bending stiffness of the whole beam.

2. All the lower order frequencies of the FGM beam decrease monotonously with the increase of the load parameter in the pre-buckling states. The fundamental frequency of the FGM beam becomes zero at the critical load. However, for the FGM beam in a post-buckling domain, the first and second order frequencies increase along with the increment of load parameters, except for the third order frequencies. The dimensionless frequency for FGM beam decreases with the increase of the gradient index $n$.

3. The numerical results show that the buckling can be reduced or delayed by adjusting the material gradient index and the distributed non-conservative force. At the same time, the adjustment of the natural frequency of the non-conservative system is realized.