Non-regularity damage evaluation in reinforced concrete structures via fragility curves

1. Introduction

Both in-plant and in-height non-regularity features have a major impact on the dynamic behaviour of structures. For example, in-plant non-regularity is responsible of torsional effects, whilst in-height non-regularity typically affects modal participation of higher modes [1], [2]. International codes approach the matter in different ways [3]-[5], but they do not consider it from a risk assessment point of view.

In this paper, in-plan and in-height damage effects are evaluated by developing fragility curves, within the Cloud Analysis framework [6]–[8].

To this aim, four reinforced concrete (RC) frames are designed based on the Italian Code provisions [4], assuming that they are located in a high seismicity zone. The structural layouts are defined to achieve different levels of non-regularity, which is measured by TIR [9]. Nonetheless, the structures are designed to stay in the same range of verifications.

To perform parametric non-linear dynamic time history analyses, a set of 61 unscaled recorded ground motions are selected. For each record, three different intensity measures (IMs) are calculated, to correlate damage and ground motion. The selected damage parameter is the demand/capacity ratio, which is calculated in terms of chord-rotation of horizontal elements. To account for record-to-record variability, a bootstrap procedure is also applied to each correlation [10]. For each linear regression, the corresponding fragility curve is hence calculated. The structures characterised by the highest non-regularity should show more fragile median fragility curves, and the dispersion of the correlation should be bigger.

2. Reference RC structures

The reference 3D buildings used in this study are four multi-storey reinforced concrete (RC) frames exhibiting varying degrees of regularity. The first structure, referred to as the “Regular Frame” (RF), features a square plan measuring 15 meters in width. The frame is further divided into three bays, each with a length of 5 meters. The seismic action is defined according to [4] for a high seismicity location. The other structures (“NRF1”, “$NRF{2}_{Q2}$” and “$NRF{2}_{Q4}$”, in the following) are designed based on the RF layout, by progressively removing bays and columns to achieve the desired levels of non-regularity (see Fig. 1).

The aim of present study is in fact to assess the seismic responses of different structures by varying their in-plan and in-height regularity. To achieve this goal, the selected structures are designed to be as similar as possible from a provisional point of view. Both the RF and NRF1 structures are hence designed adopting a behaviour factor $q=$ 3.9. To note that for torsional deformable RC structures, the Italian Code prescribes $q=$ 2. As such, to account for this difference in $q$, the NRF2 system is designed in both ways and two torsional deformable structures (“$NRF{2}_{Q2}$” and “$NRF{2}_{Q4}$”) are analysed. To account for design-given uncertainty, the response spectrum analysis results are checked to have the same level of design.

Fig. 1Reference structures: a) RF; b) NRF1 and c) NRF2

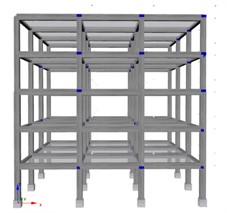
a)

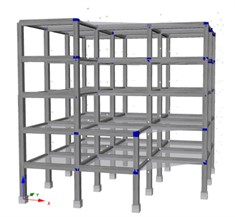
b)

c)

3. Intensity measure selection

In this work the median geometric mean value over all possible non-redundant rotation angles is used (GMrotD50) [11].

One structure-independent and two structure-dependent scalar IMs are selected among the most referred in practice, which are:

1) The Peak Ground Acceleration (PGA);

2) For structure-dependent IM, spectral acceleration is evaluated at a mean period $T_{1m}$, which is defined as the average of fundamental periods in x and y directions [9], as defined in Eq. (1):

The spectra acceleration is also evaluated as the geometric mean over a range of periods [12], [13], as expressed in Eq. (2):

Last measure is used to properly consider the rotational modes of the non-regular structures, making it a very efficient intensity measure [14]–[16]. To note that the range of periods should be selected to include higher modes effect and period elongations due to accumulation of damage. Five periods are selected in present study, including modes with mass participation higher than 10 %:

3.3. Record selection

In this work, fragility is assessed via Non-Linear Time History Analysis (NLTHAs) [17]. The Cloud Analysis procedure is selected to develop fragility curves due to its reduced computational cost of approach [18]. Moreover, it is based on the use of unscaled ground motion records avoiding possible biases introduced by scaling [19], [20].

The number of records needed for the estimation of fragility curves varies between 40 and 100 depending on the selected method of evaluation [21]–[24].

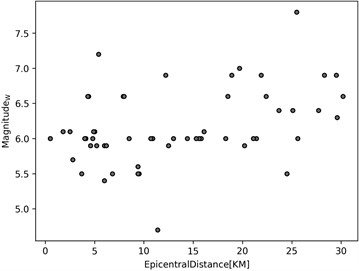
In present study, following the selection parameters in [7], a set of 61 unscaled strong ground-motion records are taken into account from the European Strong Motion Database [25]. The corresponding Magnitude – Distance scatter plot is shown in Fig. 2.

Fig. 2Magnitude – distance scatter plot

4. Results and discussion

For practical reasons, Fig. 3 shows only one IM-EDP correlation and the corresponding fragility curves.

Fig. 3Results for NRF2Q4

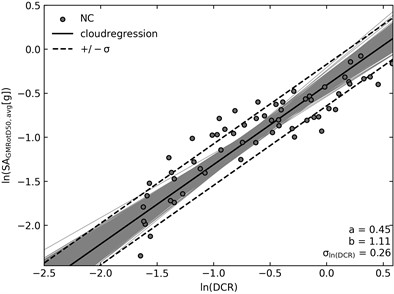
a) Linear regressions

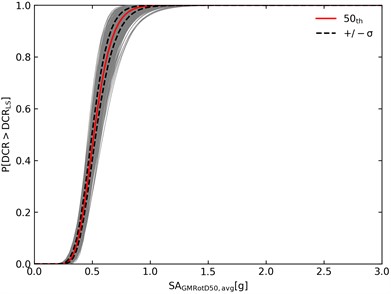
b) Fragility curves

As shown, the IM $S_{a,avg}$ trend is associated to less scatter around the mean value. This indicates that $S_{a,avg}GMRotD50$ is the most efficient IM [14], [16]. The pictures show median regression values and the confidence interval for the prediction. The dots represent IM-EDP couples. The median estimated parameters from the bootstrap procedure are also reported. The grey lines show the single bootstrap realizations.

Finally, the response of all RC structures are shown in Fig. 4: the damage evaluation is carried out by qualitatively compare the median fragility curves of reference structures.

The median linear regressions and fragility curves do not show a clear increment of fragility, which should be expected consistent / proportional to non-regularity increment. The $NRF{2}_{Q4}$ frame is the most vulnerable, meanwhile NRF1 and $NRF{2}_{Q2}$are less vulnerable. To explain this inconsistency, the total amount of accelerograms could be reduced to the highest thirty-one accelerograms which gave the highest EDP and then re-apply the whole methodology. This has been decided to account for possible bias in the record selection process. In this case, the linear regressions and the fragility curves are made without bootstrapping.

The curves are shown in Fig. 5.

Fig. 4Median regressions and fragility curves for all the examined RC structures

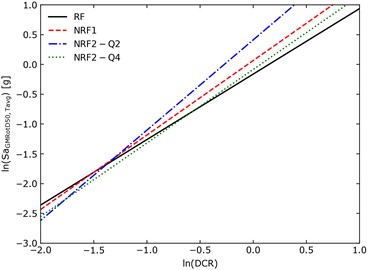
a) Linear regressions

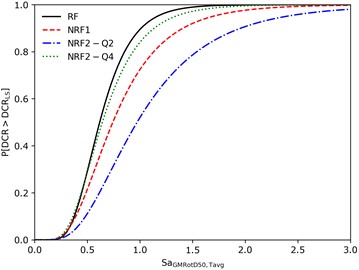
b) Fragility curves

Fig. 5Regressions and fragilities for the new seismic input

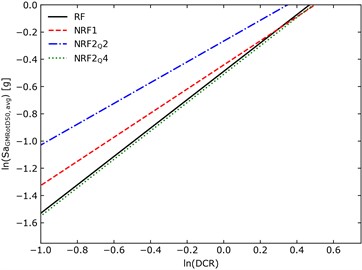
a) Linear regressions

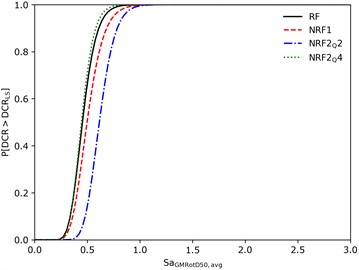
b) Fragility curves

5. Conclusions

In this paper, linear regression and fragility curves were presented, via Cloud Analysis procedure, for a selection of three-dimensional (3D) reinforced concrete (RC) frames characterized by increasing levels of non-regularity in-plan and in-height.

To this aim, the input consisted in 61 unscaled recorded ground motions. Three Intensity Measures and one local EDP were considered for the linear regression correlation. A bootstrap procedure was also implemented to account for epistemic uncertainties.

As shown, the fragility curves did not prove the expected damage incrementation with structural non-regularity, which was indeed emphasized by raw EDPs. To account for possible bias in record selection, linear regressions and fragility curves were defined for a reduced sample of accelerograms, with negligible differences in comparative outcomes.

Such an inconsistency could be probably justified by seismological aspects and statistical modelling issues. The selection of ground motions did not account for near-site effects (i.e., directivity, fling, spectral shape, etc.). Moreover, linear regression might not be the best statistical model to correlate EDPs with IMs that are not sufficient to represent the ground motion. These aspects will be thus necessarily explored in future extended studies.