Binary rat swarm optimizer algorithm for computing independent domination metric dimension problem

1. Introduction

Independent graph dominance numbers have recently been introduced in [1]. Robot navigation [2-4], network discovery and verification [5], localization of wireless sensor networks [6], combinatorial optimization [7], and applications to pharmaceutical chemistry [8] are only a few areas where metric dimension is used. Domination theory is applied in wireless communication networks [9], electrical networks [10], Backbone based routing [11], or spine based routing [12, 13] and chemical structures [14]. The independent domination set with the minimum cardinality is a logical choice for usage in any network type for information transmission.

2. Problem description

Let $d(u,v)$ be the shortest path between two vertices $u,v\in V\left(G\right)$ in the connected graph $G=(V,E)$. If the representation $r\left(v|B\right)=\left(d\right(v,x_1),d(v,x_2),...,d(v,x_k\left)\right)$ is unique for every $v\in V\left(G\right)$, then the ordered vertex set $B=\{x_1,x_2,...,x_k\}\subseteq V\left(G\right)$ is a resolving set of $G$. If every vertex of $V\backslash B$ has at least one neighbor that belongs to $B$, then $B$ is a dominating resolving set of $G$. A dominating resolving set $B$ is independent if no two vertices in $B$ are adjacent.

Let $Card\left(X\right)$ stand for the cardinality of a set $X$. The metric dimension of $G$, denoted as $dim\left(G\right)$, the domination metric dimension of $G$, denoted as $Ddim\left(G\right)$, and the independent domination metric dimension of $G$, denoted as ${\gamma }_{ir}\left(G\right)$, are as follows:

– $dim\left(G\right)=min\left\{Card\right(B):B$is a resolving set of$G\},$

– $Ddim\left(G\right)=min\left\{Card\right(B):B$is a domination resolving set of$G\},$

– ${\gamma }_{ir}\left(G\right)=min\left\{Card\right(B):B$is an independent dominating resolving set of$G\}.$

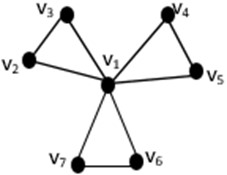
Example 2.1. The set $B=\{v_2,v_4,v_6\}$ is a minimal resolving set for the friendship graph $F_{r_7}$ given in Fig. 1, and hence $dim\left(F_{r_7}\right)=3$. Here, $B$ is also a minimal domination resolving set since every vertex of$V⧵B$ has at least one neighbor that belongs to $B$. For example, $v_3$ is adjacent to $v_1$and $v_2$. Also, $v_5$ adjacent to $v_1$ and $v_4$. In the same regard, $v_7$ adjacent to $v_1$ and $v_6$. Also, $v_1$adjacent to $v_2$, $v_3$, $v_4$, $v_5$, $v_6$ and $v_7$, and so $Ddim\left(F_{r_7}\right)=3$. On the other hand, $B$ is also independent domination resolving set of $F_{r_7}$. The set $B=\{v_2,v_4,v_6\}$ is a minimal independent domination resolving set of $F_{r_7}$, so ${\gamma }_{ir}\left(F_{r_7}\right)=3$.

Fig. 1Friendship graph Fr7

Three elements are combined in the independent domination metric dimension problem: independent, dominance, and metric dimension of graphs. Integer programming is used to discuss the difficulty of determining the metric dimension of a graph $G$ [8]. Let $D=\left[d_{ij}\right]$ be the distance matrix of $G$, $d_{ij}=d(v_i,v_j)$ for $1\le i$, $j\le n$. For $x_i\in \{0,1\}$, $1\le i\le n$, the function $F$ is defined by $F(x_1,x_2,...,x_n)=x_1+x_2+···+x_n.$

Minimizing $F$ subject to the $\left(\begin{array}{c}n\\ 2\end{array}\right)$ constraints $\left|d_{i1}-d_{j1}\right|x_1+\left|d_{i2}-d_{j2}\right|x_2+\dots +\left|d_{in}-d_{jn}\right|x_n>0$ is equivalent to finding a basis in the sense that if $x_1^{\text{'}},x_2^{\text{'}},\dots ,x_n^{\text{'}}$ is a set of values for which $F$ reaches its minimum, for $1\le i<j\le n$. Then $B=\{v_i,x_i^{\text{'}}=1\}$ is a basis for $G$ and conversely, if $B=\{v_{i1},v_{i2},\dots ,v_{in}\}$ is a basis for $G$ and if we define:

then $F(x_1^{\text{'}}$,$x_2^{\text{'}},\dots ,x_n^{\text{'}})$is a minimum subject to the given constraints.

Both the metric dimension problem and the dominant set problem are NP-complete [15, 16]. As a result, the independent domination metric dimension ${\gamma }_{ir}\left(G\right)$ is a typical NP-complete problem that involves determining if ${\gamma }_{ir}\left(G\right)\le K$ for a given graph $G$ and input $K$. The remaining part of the paper is structured as follows: A literature review is presented in Section 3. In Section 4, the Rat Swarm Optimizer Algorithm is introduced. The BRSOA for calculating the independent domination metric dimension is provided in Section 5. Results of calculations are reported in Section 6. Section 7 presents the conclusion and recommendations for future work.

3. Literature review

For a number of graphs in the literature, the metric dimension, domination metric dimension, and independent domination metric dimension are all theoretically specified. Following is a brief summary of the key recently discovered theoretical metric dimension results [17-25]. The metric dimension of subdivisions of several graphs, including the Lilly graph, the Tadpole graph, and the special trees star tree, bistar tree, and coconut tree is determined theoretically in [17], the bary centric subdivision of Möbius ladders and the generalized Petersen multigraphs in [18], trapezoid network, $Z-\left(P_n\right)$ network, open ladder network, tortoise network in [19], French windmill graph and Dutch windmill graph in [20], total graph of path power three and four in [21], two types of bicyclic graphs in [22], Mobius Ladder in [23], power of paths and complement of paths in [24], and Kayak Paddles graph and Cycles with chord in [25].

Theoretically, the independent metric dimensions are identified in [26, 27]. Cartesian product and corona of graphs are determined in [26], finite projective planes, finite biplanes in [27] and Titanium dioxide nanotube in [28]. The independent domination metric dimensions of the path graph, cycle graph, friendship graph, helm graph, and fan graph are determined theoretically in [1]. In [29, 30], the dominant metric dimension is found theoretically. The Path graph, cycle graph, star graph, complete graph, and complete bipartite graph are determined in [29], the corona product graph of $G$ and $H$ is studied whenever $H$ is a path graph, and the cycle graph, complete bipartite graph, complete graph, and star graph are determined in [30]. The connected domination metric dimensions of the complete graph, path graph, and cycle graph are determined theoretically in [31]. To compute the metric dimension problem heuristically, however, only a small number of algorithms have been presented [32-34]. For determining the metric dimension of numerous classes of graph instances, such as pseudo-Boolean, crew scheduling, and graph coloring, a genetic algorithm has been proposed in [32]. A limited number of distinct individuals with the same objective value, the binary representation, frozen gene mutation, and the caching technique were all used. Infeasible individuals are changed by the addition of the required nodes in order to become feasible. In [33], Particle Swarm Optimization is used for determining the metric dimension where an infeasible particle is mended by adding some vertices until the particle becomes feasible and a real-valued vector of vertices is converted to a binary-valued vector using a linear function. The Particle Swarm Optimization is tested by computing the metric dimension of hypercube graphs. In order to enhance the current upper bounds in [34], a variable neighborhood search method has been suggested for tackling metric dimension and minimal doubly resolving set problems. The metric dimension problem and the minimal doubly resolving set problem are divided into a series of sub problems with an auxiliary objective function as the foundation for the variable neighborhood search method. Additionally, the equivalent new integer linear programming formulations for both problems are suggested. The connected domination metric dimension problem is resolved here by encoding and adapting the operations of the equilibrium optimization algorithm. Using theoretically computed graph results, the proposed binary equilibrium optimization algorithm is put to the test and contrasted with competing techniques. Also see more details in the literature [35-38], and some future notions may be applied to some applications like [39-41]. In the binary forms of the metaheuristics, a transfer function plays a crucial role, according to Mirjalili and Lewis in [42]. It has a major effect on both the balance between exploration and exploitation and the avoidance of local optima. In 2013, Sharafi et al. [43] altered the definition of the velocity vector to the probability of mutation in each cat dimension, introduced a transfer function to the tracking mode of the cat swarm algorithm, and converted the continuous cat swarm algorithm into a discrete binary cat swarm algorithm. A binary variant of the bat technique, which is likewise a probability value that uses a transfer function to convert velocity data to updated positions, was proposed by Mirjalili et al. [44] in 2014. A discrete binary bat method (BINBA) was proposed by Sabba and Chikhi [45] in the same year to solve binary space optimization problems.

4. Rat swarm optimizer (RSO) algorithm

5. Binary rat swarm optimizer algorithm for independent dominant metric dimension

Because it maintains a population of solutions and explores a wide region to find the optimum global solution, the Rat Swarm Optimizer Algorithm can solve difficult optimization problems with several locally optimal solutions. This benefit enables a binary variant of the approach to be applied to the dominant independent metric dimension problem. Using position vectors located within the continuous real domain, search agents can navigate the search space in the continuous form of RSOA. By using an $S$-shaped transfer function to turn the continuous variable RSOA into a binary one, we may convert it to binary values. Position changes in discrete binary search space necessitate flipping between 0 and 1. The initialization phase makes use of the subsequent equation. Transfer function merits particular consideration and investigation since it plays a significant role in the discrete RSO algorithm:

where $rand(\bullet )$ refers to a random number between 0 and 1. To convert continuous values to binary ones, a transfer function is used. The sigmoid function ($S$) is applied as follows in this study:

where $S$ is the function output and $x^d$ denotes the continuous-valued location at dimension $d$. To create a binary value, use the equation below:

The proposed algorithm deals with the dominant independent resolving set problem as an optimization problem where it searches for the best solution, so each search agent can be represented as a one-dimensional vector $SA{binary}_{ij}=({SA}_{i1},\mathrm{}{SA}_{i2},...,\mathrm{}{SA}_{ij})$, for which $SA{binary}_{ij}$ is a binary-valued position vector if the $j$-th element of the vector has a value of 1, it means that vertex $j$ belongs to $B$. If every $v\in V\left(G\right)$ has a distinct representation $r\left(v\right|B)$, then $B$ is an independent dominant resolving set. The value of a binary-valued position vector is produced by computing the value of the $S$-shaped transfer function. In the BRSOA algorithm, when a search agent is not feasible as an independent dominant resolving set, that search agent is repaired by adding a vertex from $V\backslash B$. This repair is applied until that object becomes an independent dominant resolving set.

The algorithm represents each solution (individual) in the population as a string of binary in which 1 means that the independent dominant resolving set will be chosen, then the corresponding value will be “1”, and if the independent dominant resolving set is not selected, then the corresponding value will be “0”. The pseudo-code in Algorithm 1.

6. Comparison

To further demonstrate the excellence of proposed BRSOA, we choose BWOA, BPSO, BGSA, BGWO and BMFO algorithms to conduct experiments under the same conditions and compared the results. The results on graphs are shown in Tables 3-6, which indicate that proposed BRSOA algorithm, outperforms other algorithms on graphs, reaching 443.3 sec in BRSOA, 1562.4 sec in BWOA, 1239.7 sec in BPSO, 975.3 sec in BGSA, 1198.4 sec in BGWO, 1156.1 sec in BMFO for path graph and 294.3 sec in BRSOA, 739.8 sec in BWOA, 617.3 sec in BPSO, 476.8 sec in BGSA, 532.5 sec in BGWO and 761.4 sec in BMFO for cycle graph and 296.2 sec in BRSOA, 774.8 sec in BWOA, 592.8 sec in BPSO, 588.4 sec in BGSA, 596.3sec in BGWO, and 634.3 sec in BMFO for friendship graph and 356.9 sec in BRSOA, 879.3 sec in BWOA, 812.6 sec in BPSO, 786.9 sec in BGSA, 807.6 sec in BGWO and 843.7 sec in BMFO for triangular snake graph. It proves the correctness and superiority of proposed BRSOA. Figs. 2, 3, 4 and 5 show the superiority of the proposed BRSOA on the BWOA, BPSO, BGSA, BGWO and BMFO according to the independent domination resolving number.

Fig. 2The superiority of BRSOA on the BWOA, BPSO, BGSA, BGWO and BMFO

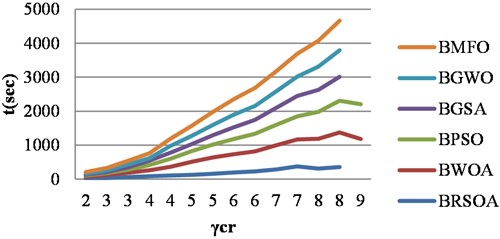
Fig. 3The superiority of BRSOA on the BWOA, BPSO, BGSA, BGWO and BMFO

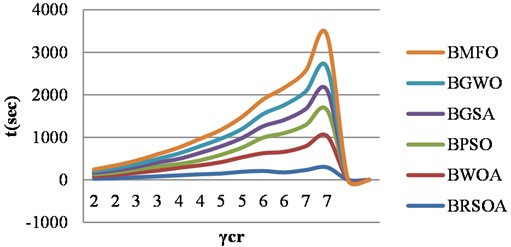
Fig. 4The superiority of BRSOA on the BWOA, BPSO, BGSA, BGWO and BMFO

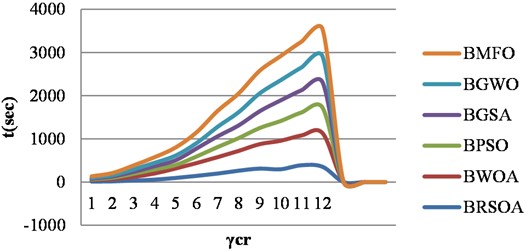
Fig. 5The superiority of BRSOA on the BWOA, BPSO, BGSA, BGWO and BMFO

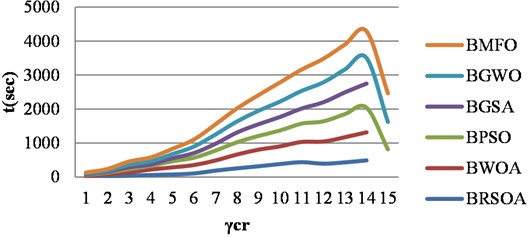
7. Conclusions

In this paper, a binary variant of the basic Rat Swarm Optimizer Algorithm (BRSOA) is adapted for determining the minimum independent domination resolving set of graphs and compared to BWOA, BPSO, BGSA, BGWO and BMFO. Comparisons were performed on the graphs: path graph, cycle graph, friendship graph and triangular snake graph. Experimental results and their analysis confirmed the superiority of the proposed BRSOA for solving the independent domination metric dimension problem. For further work in the future, we plan to compute other variants of metric dimension by other metaheuristic algorithms and compare them with competitive algorithms.