Modeling of unsteady-state creep of asphalt concrete

2.1. Materials

A hot fine-grained dense asphalt concrete of type B, meeting the requirements of the standard ST RK 1225-2013 [13], was prepared using a bitumen of grade BND 100-130, obtained at the Pavlodar petrochemical plant and meeting the requirements of the standard ST RK 1373-2013 [14]. Composition of the asphalt concrete: crushed stone – 43 % (5-10 mm – 20 %, 10-15 mm – 13 %, 15-20 mm – 10 %), sand – 50 %, mineral powder – 7 %; bitumen - 4.8 % [3, 6].

2.2. Sample preparation

The asphalt concrete samples in the shape of a rectangular beam with dimensions of 50×50×150 mm were made as follows. First, the asphalt concrete samples were prepared in the form of a slab with dimensions of 350×350×50 mm according to the standard EN 12697-33-2003 [15], which were then cut into the above beams.

2.3. Testing

The asphalt concrete samples (beams) were tested for creep under uniaxial tension at temperatures of 22-24 °C until complete failure at different stresses (from 0.084 to 0.3053 MPa). In individual tests, temperature and stress were kept constant throughout the experiment. The tests were carried out in a special installation with a heat chamber [3, 6]. 61 asphalt concrete samples were tested at seven different stresses. The elongation of the samples over time was measured by two indicators of a clock type and recorded with a video camera, which were then processed and analyzed.

3.1. Unsteady-state creep curves

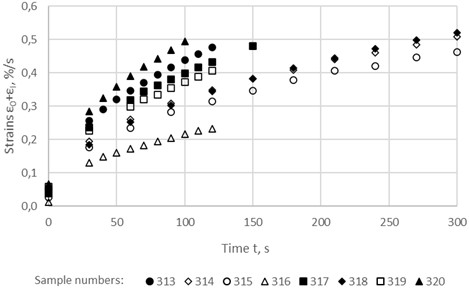
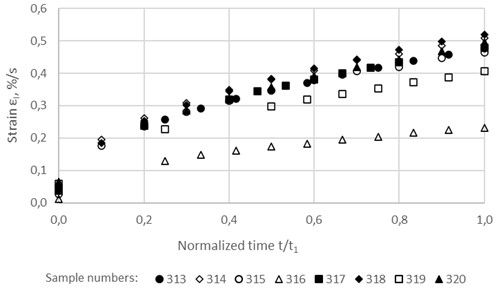
The unsteady-state creep curves of the asphalt concrete samples at two stresses (0.084 MPa and 0.1852 MPa), constructed from the test results, are shown in Fig. 1 and 2. It can be seen that the curves of parallel samples are characterized by significant heterogeneity; All characteristics are very different: conditionally instantaneous strain ${\epsilon }_{о}$, unsteady-state creep strains ${\epsilon }_I\left(t\right)$, limiting strain of hardening ${\epsilon }_1$ and limiting time of hardening $t_1$.

Fig. 1Unsteady-state creep curves of the asphalt concrete samples at a stress of 0.084 MPa

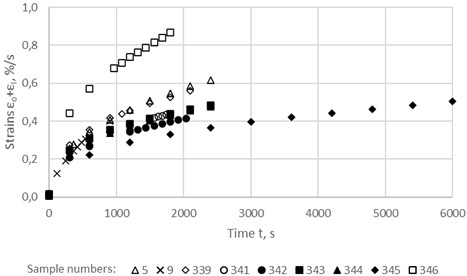
Fig. 2Unsteady-state creep curves of the asphalt concrete samples at a stress of 0.1852 MPa

Normalized versions of these curves are presented in Fig. 3 and 4, in which time is normalized in relation to the limiting time of hardening, i.e. time $t$ is replaced by the ratio $t/t_1$. The conditionally instantaneous strain ${\epsilon }_{о}$ is excluded from all curves, i.e. all creep curves represent only unsteady-state creep strains and have a zero value at $t=$0.

Fig. 3Normalized unsteady-state creep curves of the asphalt concrete samples at a stress of 0.084 MPa

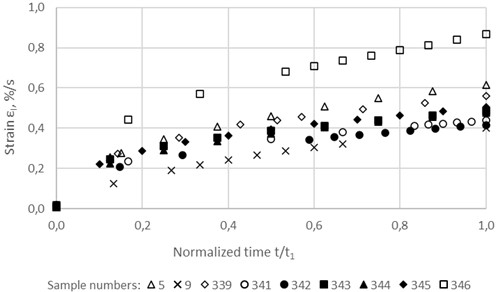
Fig. 4Normalized unsteady-state creep curves of the asphalt concrete samples at a stress of 0.1852 MPa

3.2. Approximation of unsteady-state creep curves

As noted in the introductory part of the article, the creep curve of an asphalt concrete is divided into three characteristic sections. Then the entire creep curve can be represented by the following expression:

where ${\epsilon }_{о}$ – conditionally instantaneous strain; ${\epsilon }_I\left(t\right)$, ${\epsilon }_{II}\left(t\right)$, ${\epsilon }_{III}\left(t\right)$ – unsteady-state, steady-state and accelerated creep strains, respectively.

In this article, the unsteady-state creep of the asphalt concrete is approximated by a power function of the following form:

where ${\epsilon }_1$ – limiting strain of hardening, ${\epsilon }_1={\epsilon }_I\left(t_1\right)$, %; $t_1$ – limiting time of hardening, i.e. duration of unsteady-state creep, s; $\xi$ – hardening rate.

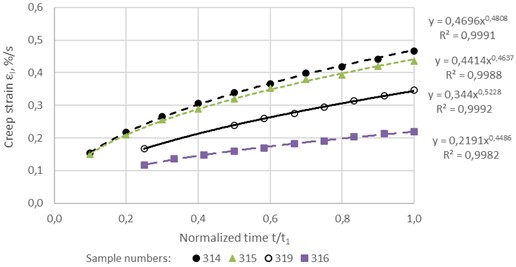
As illustrative examples, Figs. 5-6 show the experimental values of strain of the asphalt concrete samples and the corresponding approximating curves. As you can see, the degree of approximation accuracy is very high: the values of the reliability indicators ($R^2$) range from 0.9988 to 0.9999. And for all the remaining 53 samples, an approximation of the same high degree was obtained: $R_{min}^2=$0,9347; $R_{max}^2$= 1.

Fig. 5Approximation of unsteady-state creep curves of two samples (No. 5, 9, 343 and 346) of the asphalt concrete at a stress of 0.084 MPa

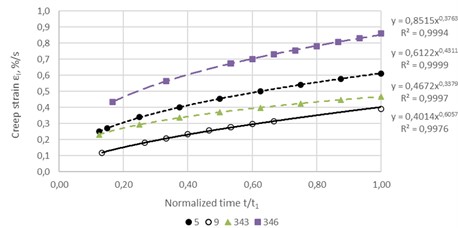
Fig. 6Approximation of unsteady-state creep curves of two samples (No. 314, 315, 316 and 319) of the asphalt concrete at a stress of 0.1852 MPa

3.3. Characteristics of unsteady-state creep

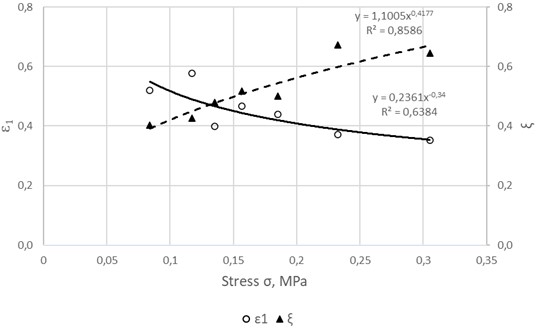
Important characteristics of unsteady-state creep of materials are the limiting time of hardening, limiting strain of hardening, and hardening rate. For the studied asphalt concrete, the dependences of these characteristics on stress are shown in Figs. 7-8.

Fig. 7Dependence of limiting time of hardening on stress

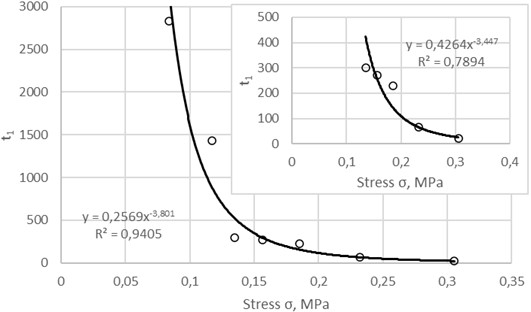
It can be seen that all of these dependencies are described with high accuracy by a power function. The most sensitive characteristic to changes in stress turned out to be the limiting time of hardening $t_1$. At a stress of 0.084 MPa, the value of $t_1$ is equal to 2826 s, and at stresses of 0.135 MPa and 0.3053 MPa it is equal to 300 s and 20.62 s, respectively, i.e. with an increase in stress by 1.6 and 3.6 times, $t_1$ decreases by almost 10 and 140 times, respectively.

The limiting strain of hardening ${\epsilon }_1$ and the hardening rate $\xi$ turned out to be relatively weakly dependent on stress. Thus, with an increase in stress by 3.63 times in the range from 0.084 MPa to 0.3053 MPa, ${\epsilon }_1$ decreases by 1.5 times, and $\xi$ increases by 1.6 times.

Fig. 8Dependence of limiting strain of hardening on stress