Abstract
To provide a reference for designers, taking a 30 m + 40 m + 30 m prestressed concrete continuous beam bridge as an example, this paper compares the differences between Chinese Codes and Southern African Codes in terms of load effect, prestressing requirements and design safety. The results show that the actual number of prestressed strands required by the Southern African Code in the mid-span section is 11.63 %-12.50 % larger than that required by the Chinese Code. The actual number of prestressed strands required by the Southern African Code in the fulcrum section is 16.33 %-30.00 % lower than that required by the Chinese Code. The safety margin factor of the section designed by the Southern African Code is higher than that of the Chinese Code, and has a higher safety reserve.
Highlights
- To provide a reference for designers, taking a 30 m + 40 m + 30 m prestressed concrete continuous beam bridge as an example, this paper compares the differences between Chinese Codes and Southern African Codes in terms of load effect, prestressing requirements and design safety.
- The actual number of prestressed strands required by the Southern African Code in the mid-span section is 11.63 %-12.50 % larger than that required by the Chinese Code.
- The actual number of prestressed strands required by the Southern African Code in the fulcrum section is 16.33 %-30.00 % lower than that required by the Chinese Code.
1. Introduction
As a periodic structure [1], [2], prestressed concrete continuous bridges have the advantages of economy, stable driving, durability, and easy maintenance. Therefore, prestressed concrete continuous bridges occupy a large proportion in the existing short and medium-span bridges in China. About 20 % of the road network of the Southern African Development Community is paved, of which mainly are short and medium-span bridges.
The Southern African Code is mainly applicable to main roads. It mainly refers to Southern African Bridge Code TMH7 [3]: Code of Practice for the design of highway bridges and culverts in Southern African, which in turn makes reference to BS5400 [4], and has been revised to be applicable to Southern African. The same as the Chinese Code, the Southern African Code also adopts the concept of limit state, which is divided into the serviceability (service) limit state and the ultimate (strength) limit state. Zhang [5] considered the differences in longitudinal and transverse distribution of traffic load between the Chinese and Southern African Codes, and carried out longitudinal influence line loading on simply supported and continuous beams. It was found that the normal load (NA) effect of the Southern African Code was more than 30 % larger than that the lane load effect of the Chinese Code, but only the NA load in the traffic load of the Southern African Code was considered, and the abnormal load (NB) and super load (NC) were not considered. It can be seen that the comparison between the Chinese and Southern African Codes is incomplete, the differences in the combination of effects, material properties, and calculation of bearing capacity are not considered.
In this paper, the bending moments of prestressed concrete continuous bridge girders with span of 30 m+40 m+30 m under dead load and traffic load of different codes is calculated, and the combination of actions and prestressing requirements of the Chinese and Southern African Codes under serviceability limit state and ultimate limit state are compared.
2. Comparison of effects
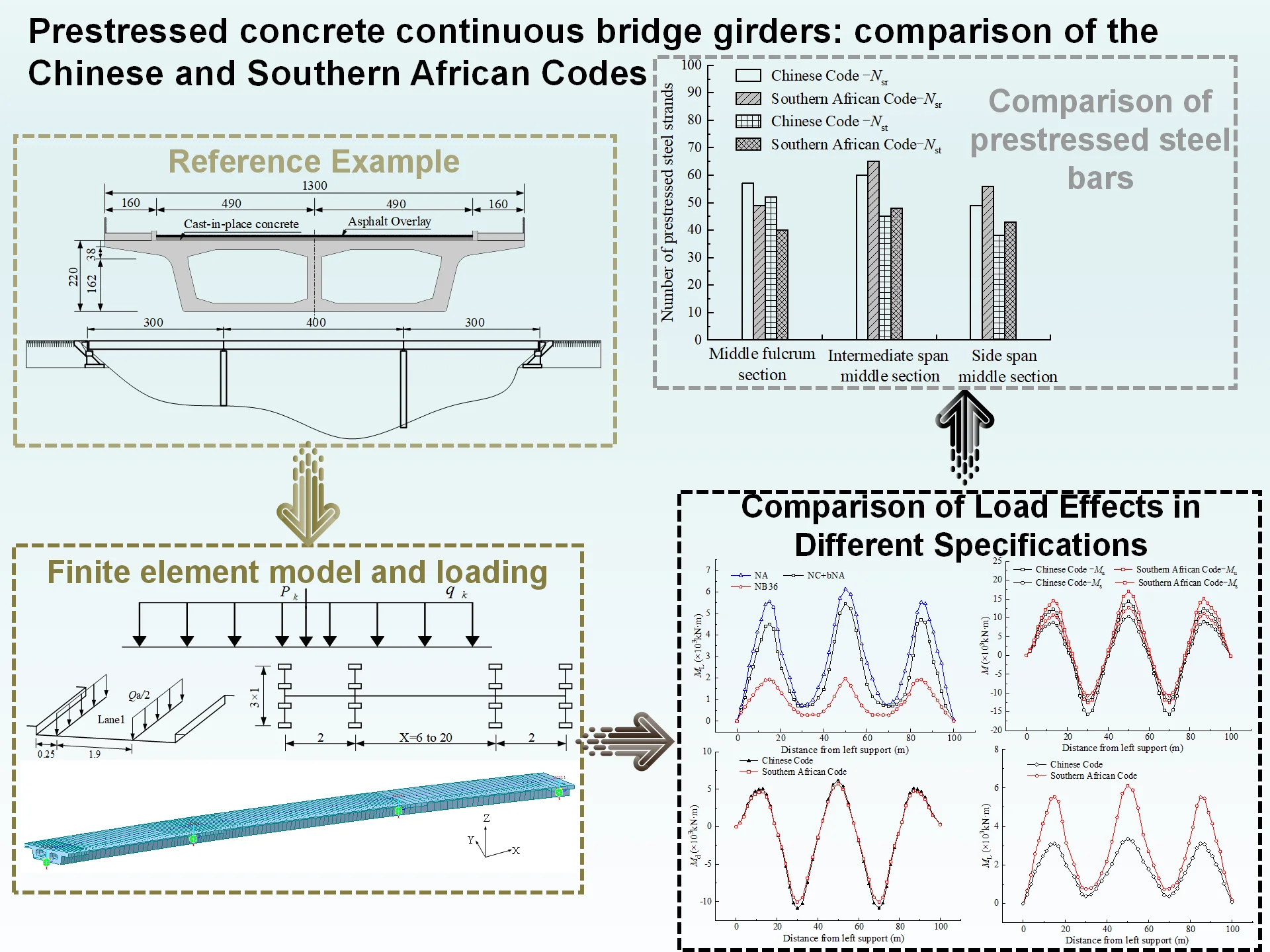
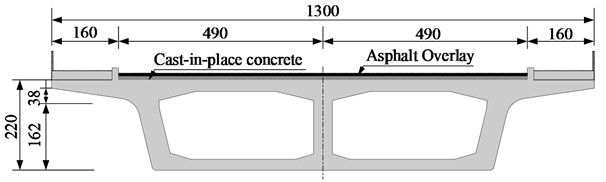
In this paper, a prestressed concrete continuous bridge in Southern African is selected as an example, and the span arrangement is 30 m+40 m+30 m. The post-tensioned prestressed concrete single-box double-chamber beam is adopted. The beam height is 2.2 m, the thickness of the flange plate is 0.2 m, and the typical section is shown in Fig. 1. The half-bridge deck is arranged as 1.6 m (sidewalk) + 4.9 m (carriageway), and the bridge deck pavement is 6 cm thick cast-in-place concrete layer and 10 cm thick asphalt pavement layer.
The MIDAS CIVIL model is used for finite element analysis. When the structure is discrete, the nodes should be set at the fixed points, supporting points and control sections of the main beam structure. All model elements are beam elements. After discretization, the calculation example has a total of 252 units and 179 nodes (Each beam element contains two nodes, a total of 12 degrees of freedom).
The continuous beam is provided with 4 supports, and the second support on the left is set as a fixed hinge support. The transverse, vertical and longitudinal displacements and the rotation around the longitudinal axis are constrained. The other three supports are set as unidirectional movable hinge supports. The vertical displacement and the rotation around the longitudinal axis are constrained. By establishing the upper and lower nodes of the support, the height of the support (0.2 m) is simulated. Rigid connections are adopted between the main beam and the upper and lower nodes of the support, and elastic connections are adopted between the upper and lower nodes of the support. The finite element model of the beam is shown in Fig. 2.
Fig. 1Prestressed concrete continuous bridge
a) Box beam cross-section (unit: cm)
b) Span layout diagram (unit: m)
Fig. 2Finite element model

The characteristic strength of concrete in the Southern African Code is the compressive strength of the cube test block with a side length of 150 mm at 28 d, with a 95 % guarantee rate, which is the same as the standard value of concrete compressive strength in the Chinese Code. The design value of compressive strength is calculated by Eq. (1) in the Southern African Code and Eq. (2) in the Chinese Code:
where: is the design value of concrete compressive strength, MPa; is the characteristic value of concrete compressive strength in the Southern African Code, MPa; is the standard value of concrete compressive strength in Chinese Code, MPa.
The box girder adopts C50 concrete, and the cast-in-place concrete layer adopts C40 concrete. The concrete parameters used for finite element analysis according to the two specifications are shown in Table 1.
Table 1Comparison of concrete parameters
Varieties | Concrete grade | Elastic modulus (MPa) | (MPa) |
Chinese Code | C50 | 3.45×104 | 23.1 |
C40 | 3.26×104 | 18.4 | |
Southern African Code | C50 | 3.40×104 | 22.3 |
C40 | 3.10×104 | 17.9 |
Prestress is provided by low relaxation high-strength steel strands in accordance with ASTM-920, with a nominal diameter of 15.2 mm, a tensile strength standard value of 1860 MPa, and a tensile strength design value of 1260 MPa [6]. The tensile strength standard values and design values of the two specifications are the same, and the material parameters of the steel strands are shown in Table 2.
Table 2Comparison of prestressed steel strand parameters
Varieties | Steel strand grade | Elastic modulus (MPa) | Tensile strength standard value (MPa) |
Chinese code | 1×7 (Shares) | 1.95×105 | 1860 |
Southern African code | ASTM-920 | 2.0×105 | 1860 |
2.1. Effects of dead load
The loads in this study only consider dead load and traffic load. The dead load includes the dead weight of the precast concrete beam, the dead weight of the cast-in-place concrete layer and the dead weight of the asphalt pavement layer. The structural weight is generally obtained by multiplying the weight of the material by the volume, which is automatically accounted for by the program. The structural weight difference between Chinese Code and Southern African Code is mainly due to the different provisions on the weight of materials. The values of material weight are shown in Table 3.
Table 3Comparison of material weight
Varieties | Material weight (kN/m3) | |
Cement concrete | Asphalt pavement | |
Chinese code | 26.0 | 23.0 |
Southern African code | 24.0 | 21.0 |
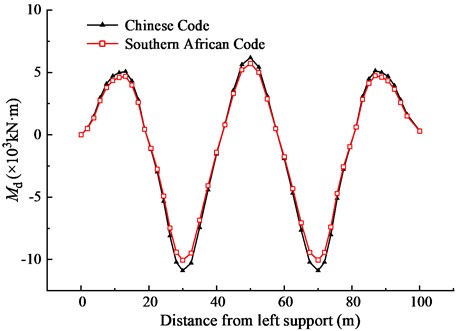
Only under dead load, the absolute value of bending moments calculated by Chinese Code is larger than that calculated by Southern African Code. As shown in Fig. 3, the positive bending moment of intermediate span middle section is the largest, which is 7019.9 kN·m in the Chinese Code and 6439.8 kN·m in the Southern African Code. The bending moment of intermediate span middle points calculated according to the Chinese Code is 9.01 % larger than that calculated according to the Southern African Code. The negative bending moment at the middle fulcrum section is the largest, which is 13062.8 kN·m in the Chinese Code and 12172.0 kN·m in the Southern African Code. The bending moment of the middle fulcrum section calculated according to the Chinese Code is 7.32 % larger than that calculated according to the Southern African Code, the Chinese Code is more conservative for the material weight.
Fig. 3Comparison of dead load effects
2.2. Effects of traffic load
The Chinese Code divides traffic load into lane load and vehicle load. As shown in Fig. 4 and Fig. 5 respectively, the Southern African Code divides traffic loads into NA load, NB load and NC load. The distribution of NA load and NB load are similar to the lane load and vehicle load in the Chinese Code, but the specific values and applications are quite different.
The Chinese Code divides the traffic load into highway-I and highway-II, including two design loads of lane load and vehicle load. The overall calculation of the bridge structure adopts the lane load, and the local load of the bridge structure and the pressure of the abutment and retaining wall are calculated by vehicle load. The effect of lane load and vehicle load should not be superimposed [7].
In finite element analysis, the lane load is selected as the traffic load loading mode, and the grade is highway-I. The standard value of uniform load of highway-I lane load is = 10.5 kN/m. The standard value of concentrated load is related to the calculated span, and the value is shown in Table 4. The calculated span represents the horizontal distance between the center of the adjacent two supports with the support.
Fig. 4Lane load diagram
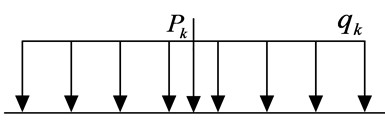
Table 4The value of concentrated load Pk
The calculated span (m) | 5 | 5 << 50 | ≥ 50 |
(kN) | 270 | 2 (+130) | 360 |
The transverse distribution of vehicle load is shown in Fig. 6. In the Chinese Code, the number of lane loads is related to the width of the bridge deck and the driving mode of the vehicle. When multiple lane loads are arranged in the transverse direction of the bridge, the reduction of lane loads should be considered according to Table 5. For a bridge with two-way driving and 13 m bridge deck width, the number of design lanes is 2, and the lateral lane loading coefficient is 1.0. When it is a multi-span continuous structure, the whole structure should consider the longitudinal reduction of the vehicle load effect according to the maximum calculation span, where the longitudinal reduction coefficient is 1.0.
Fig. 5Vehicle load diagram (size unit: m; load unit: kN)
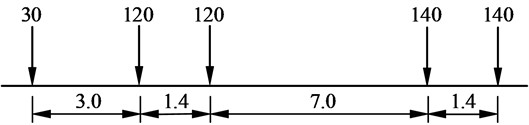
a) Facade
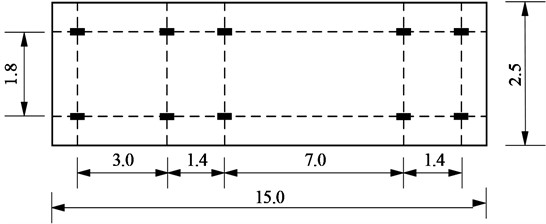
b) Plane
Fig. 6Vehicle load transverse layout diagram (unit: m)
Table 5Lateral lane loading coefficient
Number of lateral loading lanes | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Lateral lane loading coefficient | 1.20 | 1.00 | 0.78 | 0.67 | 0.60 | 0.55 | 0.52 | 0.50 |
The standard value of the impact force of the traffic load in the Chinese Code is calculated by multiplying the standard value of the traffic load by the impact coefficient. The impact coefficient can be calculated according to Eq. (3):
where: is the fundamental frequency of the structure.
In the finite element analysis of load combinations, according to the Southern African Code [8], the traffic load includes the normal load (NA), abnormal load (NB) and super load (NC). The effect of traffic load should take the most unfavorable situation under the action of NA, NB and NC+bNA. For small and medium-span bridges, the NB load effect is generally greater than the NA load effect, and the opposite is true for large-span bridges, and it is necessary to consider the combination of NA load and NC load., that is, NC + bNA, where 2/3.
The notional lane is used in the Southern African Code, which is only used to apply the specified traffic load. It is stipulated that the widthof a single nominal lane should not be less than 2.4 m or more than 3.7 m, and the lane should be divided into the corresponding number of nominal lanes. The relationship between the width of the lane and the number of nominal lanes is shown in Table 6.
Table 6Number of notional lanes per carriageway width [8]
Lane width (m) | 4.8 7.4 | 7.4 11.1 | 11.1 14.8 | 14.8 18.5 | 18.5 22.2 |
Number of notional lanes | 2 | 3 | 4 | 5 | 6 |
NA load is composed of uniform load and concentrated load, which is similar to the lane load in the Chinese Code. It is mainly used for the overall stress analysis of the structure and is the most basic load requirement in bridge structure checking. The uniform load is related to the loading length. The concentrated load is 144/ kN, and n is the loading sequence number of the corresponding notional lane:
where: is the effective loading length (m) of uniform load; is the average load per meter of notional lane (kN/m).
is the total length of a single part loaded in any single lane or multiple notional lane combinations, that is, the sum of the lengths of all lanes in the transverse direction loaded according to the influence line. The loading lengths in each lane are not necessarily equal, and the loading lengths in the same lane may also be discontinuous. When 36 m, , and are the loading length of the three notional lanes respectively, may be 20 m, is 10 m, is 6 m, and the concentration of these three blocks is 36 kN/m. The remaining loading part is derived according to the formula to derive the loading strength and perform lane loading. can be expressed as the loading length consisting of separate parts, then the load strength on the is shown in Eq. (5):
where: is the th loading length (m), and is the uniform load (kN/m) of the th loading part.
Different from the Chinese Code, the Southern African Code directly considers the reduction of each lane when the load value is taken, and the concentrated load value applied to each lane is not equal. Only one NA load can be applied on each lane, which is loaded on the most unfavorable position of the influence line of the notional lane. The concentrated load and the uniform load should be applied at the same time. When the lateral load of the lane has a significant effect on the bearing member, the lateral load of the NA concentrated load should be applied in two equal concentrated loads. The uniform load adopts two linear loads with equal strength. The size of the line load is /2 kN/m, the load spacing is 1.9 m, the load is parallel to the direction of the lane, and the load is applied in the most unfavorable position. The loading method is shown in Fig. 7.
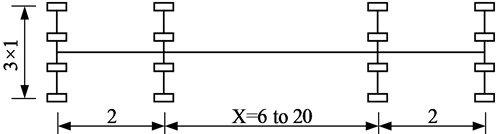
The NB load represents a single unconventional heavy vehicle, which is a unit load. Each axle is composed of four wheels, and the axle between the two inner shafts changes as shown in Fig. 8 to produce the most unfavorable effect. The overall form is similar to the vehicle load form in the Chinese Code. Fig.8 lists the plan and longitudinal layout of NB load. The axle load per unit NB load is 10 kN, as shown in Fig. 8(b). There are two types of NB loads, NB24 and NB36, which are 24 and 36 unit loads, respectively.
Fig. 7NA uniform load transverse distribution (unit: m)
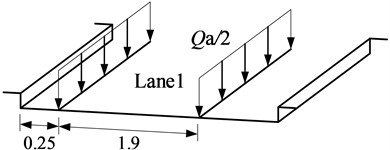
Fig. 8NB load layout (size unit: m; load unit: kN)
a) Plane
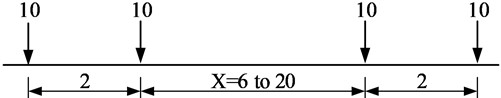
b) Facade
In view of the fact that the traffic load in the Southern African specification is developed from the BS5400 [4], referring to the corresponding HB load, it can be seen that the NB load is loaded separately in the longitudinal direction, and other traffic loads are not considered. The NB load can be loaded across the notional lane horizontally and is not constrained by the notional lane.
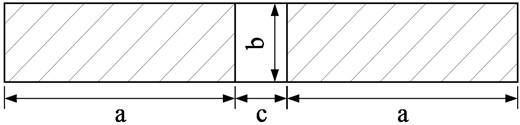
The combined load of multi-wheel trailer represented by NC load is equivalent to the load of trailer in the Chinese Code, which is used for special checking calculation of bridge structure. Fig. 9 shows the layout of the standard type NC-30×5×40 load, where a can be 5, 10, 15 and 20 m, b can be 3,4 and 5 m, and c can be 0, 5 to 25 m.
Fig. 9NC load plane loading area diagram
The Chinese Code calculates the impact of vehicle load separately based on the span and cross-section of the bridge [7], while the standard values of the traffic load in the Southern African Code take into account a certain vehicle impact coefficient. The bending moment generated by the traffic load here contains the impact effect. For a bidirectional bridge with a deck width of 13 m, the design lane number of Bridges and culverts is 2 in the Chinese Code of finite element analysis, and the nominal lane number is 4 in the Southern African Code of finite element analysis. The transverse lane distribution coefficient of the finite element analysis model is 1.0. The bending moment of continuous beams under NA load, NB36 load and NC + bNA load is shown in Fig. 10. The bending moment of the beam under NA load is the largest, and the intermediate span middle section is 6126.64 kN·m. The bending moment of the beam under the load of NB36 is the smallest, the intermediate span middle section is 2168.89 kN·m. Among them, NA load plays a controlling role.
Fig. 10Comparison of traffic load effects in Southern African code
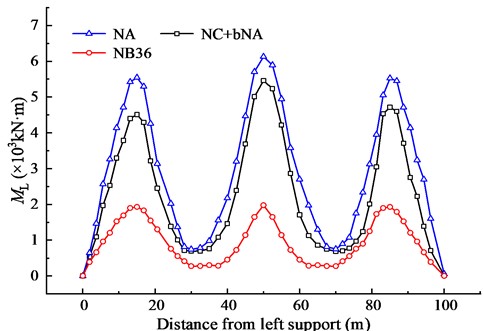
Fig. 11Comparison of traffic load effects
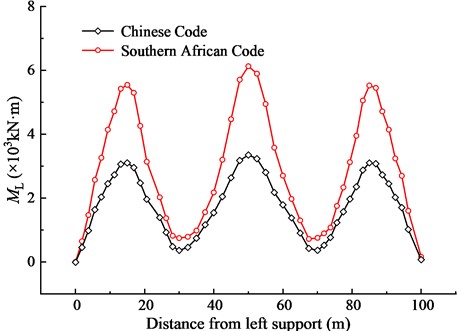
As shown in Fig. 11, under the action of traffic load, the absolute value of bending moment calculated according to the NA vehicle load of the Southern African Code is larger than that of the Chinese Code highway-I lane load. The bending moment of the intermediate span middle section calculated according to the Chinese Code is 3351.6 kN·m, and the bending moment of the middle fulcrum section calculated according to the Southern African Code is 6126.6 kN·m, which is 82.80 % larger than that of the Chinese Code. It can be seen that the traffic load value and loading method in the Southern African Code are more conservative than those in the Chinese Code.
2.3. Combination of effects
It can be seen from the combination of the Chinese and Southern African Codes that the coefficients of the serviceability limit state and ultimate limit state are different. Even under the same specification, for the same limit state, the load coefficient may be different for different design live loads. In the Southern African Code, the load coefficients of NA load are also different from those of NB and NC + bNA loads. This paper only lists the load coefficients or formulas related to the considered conditions. The bending moment under the serviceability limit state is mainly used to check the tensile stress of concrete, while the bending moment under the ultimate limit state mainly controls the minimum bending capacity required.
The Southern African Code selects combination 2 including permanent and variable effects, and the Chinese Code selects the corresponding quasi-permanent combination under the serviceability limit state and the basic combination under the ultimate limit state. The design effect of the serviceability limit state and the ultimate limit state of the Chinese and Southern African Codes is shown in Eqs. (6-8). The and of each control section in the serviceability limit state and ultimate limit state of the Chinese and Southern African Codes are calculated respectively, as shown in Fig. 12.
Chinese Code:
where: is the effect design value of the quasi-permanent combination; is the effect function of action combination; is the quasi-permanent value coefficient of vehicle load; is the effect design value of the basic combination; is the structural importance coefficient; is the partial coefficient of permanent action; is the standard value of permanent action; is the partial coefficient of vehicle load; is the standard value of vehicle load; the partial coefficient of variable action effect in the action combination except for the vehicle load and the wind load; is the standard value of variable effect in the action combination except for the vehicle load; is the combination coefficient of other variable actions in the action combination except for the vehicle load effect; it is the variable structural design life load adjustment coefficient.
Southern African Code:
where: is the design effect; is the nominal role; is the unfavorable condition coefficient considering the load deviation from the standard value; is the combination coefficient considering the simultaneous action of multiple loads; is the coefficient introduced considering the inaccurate load estimation, unforeseen stress distribution or inaccurate structural size caused by construction.
The effect combination coefficients of Chinese and Southern African Codes under ultimate limit state and serviceability limit state are shown in Table 7.
Table 7The effect combination coefficient under ultimate limit state and serviceability limit state
Limit state | Varieties | Dead load | Traffic load |
Ultimate limit state | Chinese code | 1.2 | 1.4 |
Southern African code (·) | 1.05 | 1.3 | |
Serviceability limit state | Chinese code | 1.0 | 0.4 |
Southern African code (·) | 1.0 | 1.0 |
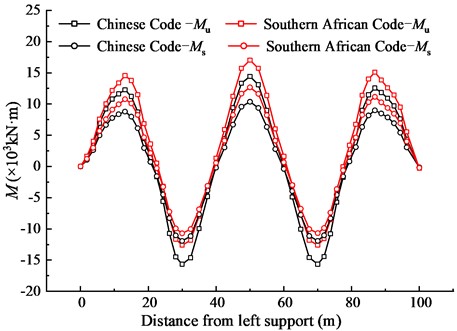
As shown in Fig. 12, the bending moment response of the load combination varies greatly between the mid-span and fulcrum sections. Under the ultimate limit state, the positive bending moment of the intermediate span middle section is the largest, which is 14424.19 kN·m in the Chinese Code and 17042.29 kN·m in the Southern African Code, which is 18.15 % larger than that in the Chinese Code. In addition, the maximum positive bending moment of the side span in the Southern African Code is 20.26 % higher than that of the Chinese Code. The negative bending moment of the middle fulcrum section is the largest, which is 15664.93 kN·m in the Chinese Code and 12621.46 kN·m in the Southern African Code, which is 19.43 % smaller than that in the Chinese Code.
Under the serviceability limit state, the positive bending moment of the intermediate span middle section is the largest, which is 10369.01 kN·m in the Chinese Code and 12670.07 kN·m in the Southern African Code, which is 22.19 % larger than that in the Chinese Code. In addition, the maximum positive bending moment of the side span in the Southern African Code is 24.10 % higher than that of the Chinese Code. The negative bending moment of the middle fulcrum section is the largest, which is 11927.51 kN·m in the Chinese Code and 10704.51 kN·m in the Southern African Code, which is 10.25 % smaller than that in the Chinese Code.
Fig. 12Comparison of the combination of effects
3. Comparison of prestressing requirements
Reasonable configuration of prestressed strands is the key to the design of prestressed concrete bridge structures. The most intuitive way to compare the prestressing requirements of each specification is to compare the number of prestressed strands required. The Chinese Code stipulates that in the serviceability limit state, tensile stress is not allowed at the tensile edge of the normal section, that is, tensile stress should not appear in the preloading area of prestressed concrete members including dead and live loads. According to the Southern African Code, for the first type of design member, under the serviceability limit state, the member should be a fully prestressed structure, and there is no tensile stress in the section, that is, the allowable tensile stress of concrete is 0. To facilitate comparison, the research requirements of bridge prestressing requirements only consider the number of prestressed strands, regardless of the number of ordinary strands.
According to the specified material properties, the tensile strength of the prestressed strands is 1860 MPa, and the initial stress is 0.75 or 1395 MPa, and the cross-sectional area of the prestressed strand is calculated. The basic principles of the formulas satisfying the limit state in the specification are the same, but the material design strength and design parameters are different. When estimating the prestressed strands, it is necessary to calculate the number of prestressed strands in the serviceability and ultimate limit states of the structure.
3.1. Serviceability limit state
Both the Chinese and Southern African Codes stipulate that prestressed concrete flexural members should check the tensile stress of normal section concrete to meet the crack resistance requirements of normal sections. In the Chinese Code, when the number of prestressed strands of concrete structures is designed according to the requirements of the serviceability limit state, the stress should meet Eq. (9) and Eq. (10).
Chinese Code:
Southern African Code:
where: is the normal tensile stress of the edge concrete under the short-term effect combination of action (or load), and the formula does not contain positive and negative signs; is the pre-compression stress generated by the pre-loading after deducting all the prestress losses at the edge of the crack resistance check of the flexural member.
The above formula can be written as Eq. (11) and Eq. (12) according to the crack resistance requirements of the upper and lower edges of the section, and the calculation formula of the Chinese Code contains 0.85:
where: and are the combination of action (or load) effects, the maximum and minimum values of bending moment; is the permanent prestress of prestressed steel bar; and are the distances between the pre-stressed strands on the upper and lower sides of the cross-section centroid axis and the centroid axis, and the values of the same section in the Chinese and Southern African Codes are the same; and are the bending modulus of the upper and lower edges of the section.
Combined with the allowable tensile stress of concrete, it can be seen that the calculation principles of flexural bearing capacity in the Chinese and Southern African Codes are the same. According to the section characteristics, the minimum number of prestressed strands required for each control section is obtained. The calculation results are shown in Table 8. The key sections with large internal forces in each span are listed for comparison, and the remaining sections are not listed.
Table 8The minimum number of prestressed strands that meet the serviceability limit state
Section position | Intermediate span middle section | Side span middle section | Middle fulcrum section |
Chinese code | 60 | 49 | 57 |
Southern African code | 65 | 56 | 49 |
3.2. Ultimate limit state
When the prestressed concrete structure reaches the ultimate limit state, the tensile strand first reaches the yield strength, and finally, the concrete in the compression zone is crushed. The tensile strength of the tensile strand and the compressive strength of the concrete are fully utilized when the beam is destroyed [10]. When estimating the number of prestressed strands, for the box section, when the height of the compression zone is located in the compression flange, the number of prestressed strands required by the structure can be obtained by the force balance and bending moment balance equations, which can be calculated according to the following formula. The calculation results are shown in Table 9.
Chinese Code:
Southern African Code:
where: is the strength bending moment of the section; is the tensile stress of the strand when the section is damaged by bending; is the area of prestressed strands in the tension zone; is the distance from the strength compression edge to the center of mass of the prestressed strand, is the height of the compression zone.
Table 9The minimum number of prestressed strands that meet the ultimate limit state
Section position | Intermediate span middle section | Side span middle section | Middle fulcrum section |
Chinese code | 45 | 38 | 52 |
Southern African code | 48 | 43 | 40 |
The calculation of the prestressed beam not only meets the prestressing requirements under the two limit states but also ensures that the stress of the concrete is within the allowable range of the specification. The maximum amount of strands required for the mid-span and the fulcrum sections is shown in Fig. 13. In the Chinese and Southern African Codes, the number of strands required to meet the serviceability limit state is greater than the number of strands required to meet the ultimate limit state . It can be seen that the serviceability limit state of the concrete allowable stress determines the structural design.
Fig. 13Comparison of prestressed strands under different limit states
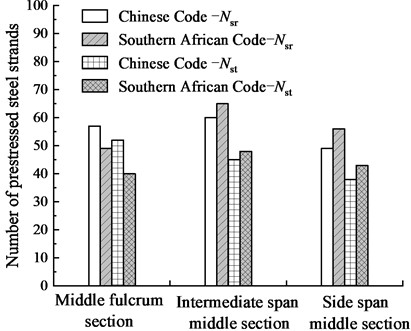
Under the ultimate limit state, the number of strands required for the design of the side span middle sections under the Chinese Code is 11.63 % smaller than that of the Southern African Code, and the number of strands required for the design of the middle fulcrum section under the Chinese Code is 30.00 % larger than that of the Southern African Code; Under the serviceability limit state, the number of strands required for the design of the side span middle section according to the Chinese Code is 12.50 % smaller than that according to the Southern African Code, and the number of strands required for the design of the middle fulcrum section according to the Chinese Code is 16.33 % larger than that according to the Southern African Code. Compared with the Southern African Code, the Chinese Code is more economical for the reinforcement design in the positive bending moment area and more conservative for the reinforcement design in the negative bending moment area.
To intuitively compare the serviceability limit state and the ultimate limit state, the ratio of the number of prestressed strands is used to represent the ratio of the number of prestressed strands required to meet the crack resistance requirements under the serviceability limit state to the number of prestressed strands required to meet the ultimate limit state [11]:
The calculation results are shown in Table 10.
Table 10The ratio of the number of prestressed strands in different limit states of the Chinese and Southern African codes
Section position | Intermediate span middle section | Side span middle section | Middle fulcrum section |
Chinese code | 1.33 | 1.29 | 1.10 |
Southern African code | 1.35 | 1.30 | 1.23 |
The ratio of Chinese Code is 1.10-1.33, and the ratio of Southern African Code is 1.23-1.35. The ratio of the number of prestressed strands required for the serviceability limit state and the ultimate limit state of the two specifications is greater than 1, indicating that the bridge in the serviceability limit state exceeds the minimum value of the prestressed strands required for the ultimate limit state, and the safety margin factor of the intermediate span middle section is the largest. The safety margin from normal use to failure of the section designed according to the Southern African Code is greater than that of the Chinese Code.
4. Conclusions
In this paper, the prestressed concrete continuous girders designed according to the Chinese and the Southern African Codes are studied, the differences of load effects in different Codes are analyzed. By comparing and analyzing the differences of load combination and prestressing requirements under limit states, the following conclusions can be drawn:
1) Under the actions of dead load, the absolute moments calculated according to the Chinese Code are larger than the calculated according to the Southern African Code. The moment of the intermediate span middle section calculated according to the Chinese Code is 9.01 % larger than that of the Southern African Code, and that of middle fulcrum section calculated according to the Chinese Code is 7.32 % larger than that of the Southern African Code.
2) There is a big difference between the Chinese and the Southern African Code in terms of traffic load. In the Southern African Code, NA load has the largest moment and plays a controlling role. The absolute moments calculated according to the Southern African NA load are larger than that of the Chinese highway-I lane load, in which the moment of the intermediate span middle section is 82.80 % larger than that of the Chinese Code. The value and loading methods of the traffic load in the Southern African Code are more conservative than those of the Chinese Code.
3) Considering the load combination under the ultimate limit state, the positive moment of the intermediate span middle section calculated according to the Southern African Code is 18.15 % larger than that of the Chinese Code, and the negative moment of middle fulcrum section calculated according to the Southern African Code is 19.43 % smaller than that of the Chinese Code. Under the serviceability limit state, the positive moment of the intermediate span middle section calculated according to the Southern African Code is 22.19 % larger than that of the Chinese Code, and the negative moment of middle fulcrum section calculated according to the Southern African Code is 10.25 % smaller than that of the Chinese Code.
4) Under the ultimate limit state, the number of strands required by the side span middle section designed according to the Chinese Code is 11.63 % smaller than that of the Southern African Code, and the number of strands required by the middle fulcrum section designed according to the Chinese Code is 30.00 % larger than that of the Southern African Code. Under the serviceability limit state, the number of strands required by the side span middle section designed according to the Chinese Code is 12.50 % smaller than that of the Southern African Code, and the number of strands required by the middle fulcrum section designed according to the Chinese Code is 16.33 % larger than that of the Southern African Code.
5) The ratio between the serviceability and ultimate limit states of the prestressing strands required by the Chinese Code is smaller than that required by the Southern African Code. The safety margin of the section designed according to the Southern African Code from service to strength is larger than that of the Chinese Code.
The research in this paper can provide reference for designers and promote the improvement of the codes in China and Southern African. However, this paper only compares one type span layout continuous beam bridge, and the differences between Chinese and Southern African Codes can be compared based on different spans and different bridge types.
References
-
C. Pany, “An insight on the estimation of wave propagation constants in an orthogonal grid of a simple line-supported periodic plate using a finite element mathematical model,” Frontiers in Mechanical Engineering, Vol. 8, p. 92655, Jul. 2022, https://doi.org/10.3389/fmech.2022.926559
-
C. Pany and G. Li, “Editorial: Application of periodic structure theory with finite element approach,” Frontiers in Mechanical Engineering, Vol. 9, p. 11926, Apr. 2023, https://doi.org/10.3389/fmech.2023.1192657
-
“Code of practice for the design of road bridges and Culverts. Part 3: Code of practice for the design of road bridges and Culverts in Southern African,” Department of Transport, Southern African, 1989.
-
“Steel, concrete and composite bridges. Part 4: Code of practice for the design of concrete bridges,” British Standards Institute, London, 1990.
-
B. Y. Zhang, M. D. Zhou, and M. Huang, “Contrastive study of traffic loads in SATCC and JTG D06-2004,” (in Chinese), World Bridges, Vol. 43, No. 1, pp. 75–78, 2015.
-
“Code of practice for the design of road bridges and Culverts. Part 1: general statement,” SATCC, Southern African, 1998.
-
“Specifications for design of highway reinforced concrete and prestressed concrete bridges and culverts,” People’s Communication Press, Beijing, 2018.
-
“Code of practice for the design of road bridges and culverts. Part 2: Specification for loads,” SATCC, Southern African, 1998.
-
G. Y. Guo and F. H. Dong, “Comparative analysis of certainty and reliability of prestressed concrete continuous beam bridge based on Chinese and American Code design,” (in Chinese), Journal of China and Foreign Highway, Vol. 36, No. 5, pp. 132–138, 2016, https://doi.org/10.14048/j.issn.1671-2579.2016.05.029
-
S. T. Wang, Y. P. Zhang, and Z. J. Feng, “Comparative analysis of methods for estimating the number of prestressing tendons in prestressed concrete bridges,” (in Chinese), Highways and Automotive Applications, No. 6, pp. 178–181, 2012.
-
J. S. Du and F. T. K. Au, “Deterministic and reliability analysis of prestressed concrete bridge girders: comparison of the Chinese, Hong Kong and AASHTO LRFD Codes,” Structural Safety, Vol. 27, No. 3, pp. 230–245, Jul. 2005, https://doi.org/10.1016/j.strusafe.2004.10.004
About this article
The authors would like to gratefully acknowledge the financial support by Science and Technology Project of China Highway Engineering Consulting Corporation (zzkj-2022-04).
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Junping Wang: conceptualization, data curation, methodology, software. Xiaosong Mi: funding acquisition, methodology, visualization. Lifeng Li: methodology, conceptualization, data curation. Shuhua Liu: supervision, validation, visualization, writing-original draft preparation. Daoyu Wang: writing-original draft preparation, data curation, formal analysis, software. Sen Liu: writing-review and editing, writing-original draft preparation, visualization.
The authors declare that they have no conflict of interest.
