Effect of welding axial stresses on the strength of a welded pipe joint with a defect

1. Introduction

Modern approaches to the operation of pipeline transport are focused on extending the service life beyond the standard service life. This is mainly due to significant investments in the renewal of individual sections of the pipeline's line part by replacing them completely. However, if pipe damage is isolated and minor, it is advisable to first assess its static strength under certain operating conditions. At the same time, fluctuations in internal pressure should be taken into account, which can accelerate the initiation and growth of crack-like defects [1].

The results of in-pipe inspection of main pipelines using ultrasonic and magnetic methods show that the depth of defective zones can range from 20 to 70 % of the pipe wall thickness. Defects are typically located at the outer surface of the pipe in its upper and lower parts [2, 3]. However, weld defects are also observed, especially in annular welds [3]. Such weld joints are performed in the construction site and are more exposed to harmful external influences.

In order to increase operational loads, high-strength materials are now widely used in the manufacture of pipes of the X80-X100 type. These materials reduce the metal consumption of the structure and provide a higher flow capacity (increased pressure of the transported product). However, welding of such materials is accompanied by difficulties in obtaining equally strong joints [4]. The use of special metallurgical and technological techniques leads to the formation of structural heterogeneity in the welded areas [5]. A complicated stress state is also formed due to local heating of the joint during arc welding [6]. Therefore, when estimating the static strength of a pipeline, operational loads and characteristics of the magnitude and distribution of residual weld stresses should be taken into account.

2. Literature review

In the special regulatory literature [7, 8], the issue of assessing the static strength of main pipelines is focused on the use of the two-parameter brittle - tough fracture criterion R6. It makes it possible to assess the performance of the pipeline under the influence of internal pressure and under the presence of various defects in the pipe material, including those at the inner and outer surfaces. Paper [9] shows the possibility of taking into account external additional forces caused by the action of global bending moments due to the peculiarities of the pipeline design – its aboveground segment. The effect of residual weld stresses in pipelines which are made of low-alloy steels on the static strength of pipelines with defects based on the use of the two-parameter brittle-tough fracture criterion R6 was studied in [2, 3, 6]. However, this issue has not been fully expanded in the case of high-strength steels.

Welding of high-strength steels results in a more complicated distribution of residual welding stresses. They do not always reach their maximum on the weld axis, and the highest values can often be localized in the fusion zone or heat affected zone [10, 11]. The peculiarities of using such welds are well described in [4, 5]. The structure of the base metal is predominantly bainitic, and the welds are ferritic-pearlite or austenitic. At the same time, the use of arc welding in high-strength steel joints requires a certain level of cooling rates [12] to achieve the required crack resistance.

The literature widely presents computational methods for modelling welding stresses and shows the possibility of using non-destructive physical methods to solve such problems [2, 3, 6, 13]. However, if the operating conditions were not monitored regularly, it is difficult to predict the character and level of the residual stress-strain state, and it is not always possible to determine it experimentally because of the localization of weld stresses only in the vicinity of the weld. In this case, the use of the experimental-calculation method is preferable. The main provisions of this method for different types of connections are given in the specialized literature [2, 3, 6, 14]. However, in the case of high-strength steels, this approach is not fully presented.

3. Research methods

Modeling of residual welding stresses. To determine the residual stresses, we used the methodology of the experimental-calculation method, which is widely presented in [2, 3, 6, 15]. This method is based on the preliminary determination of residual plastic deformations that occurred in the vicinity of the weld as a result of the thermal cycle of welding.

At the same time, the use of materials that are prone to low-temperature transformations during cooling of the welded joint requires a more detailed consideration of the mathematical model of the experimental-calculation method. In particular, there may be cases where plastic deformations reach their maximum values at some distance from the weld axis. As a result of summarizing the known experimental and theoretical data [2, 3, 6, 15], the residual plastic strains in the annular ($e_{\beta \beta }^0(\alpha ,\gamma )$) and axial ($e_{\alpha \alpha }^0(\alpha ,\gamma )$) directions can be represented as follows:

where $\alpha =z/R$, $z$ is the coordinate of the point along the axis of the pipe (the origin is chosen at its median surface with the radius $R$); $\gamma$ is the coordinate along the outer normal to the median surface; $S_i^0\left(\alpha \right)=1$ if $\left|\alpha \right|\le {\alpha }_i$; $S_i^0\left(\alpha \right)=0$ if $\left|\alpha \right|>{\alpha }_i$; ${\alpha }_i=b_i/R$; $b_i$ are the coordinates of the plastic deformation zone; ${\phi }_i\left(\alpha \right)=1+s_i{\alpha }^2/{\alpha }_i^2-\left(3+2s_i\right){\alpha }^4/{\alpha }_i^4+\left(2+s_i\right){\alpha }^6/{\alpha }_i^6\text{;}$$f_i\left(\gamma \right)=1+q_i\gamma /h-n_i{\gamma }^2/h^2$, $q_i<n_i<1$, $h$ is the half-thickness of the shell; $i=$0, 1, 2, 3, 4; ${\epsilon }_i^{\mathrm{*}}$, $q_i$, $n_i$, $s_i$, ${\rho }_0$, ${\rho }_3$ are numerical parameters determined by means of using the experimental data.

The function ${\varphi }_i\left(\alpha \right)$ characterizes the distribution of plastic deformations along the generatrix pipe, and $f_i\left(\gamma \right)$ characterizes their variation over the pipe thickness. Such distributions make it possible to describe the field of plastic deformation in accordance with the peculiarities of the physical and mechanical characteristics of high-strength steels. As a result of applying the approaches proposed in [2, 3, 6, 15], we obtain a direct solution to the problem of calculating the residual axial ${\sigma }_{\alpha \alpha }$ and annular ${\sigma }_{\beta \beta }$ stresses at an arbitrary point of the pipe caused by residual deformations due to welding.

Static strength of the pipeline. To determine the static strength of pipes with an external axial crack-like defects under the action of internal pressure $p$ in the zone of weld residual stresses, we apply a two-parameter criterion of brittle-tough fracture, justified on the basis of numerous literature data [2, 3, 6, 14]:

where $K_r=K_1/K_{1c}$ is a dimensionless stress intensity factor (SIF) characterizing the brittle fracture mechanism; $K_{1c}$ is the critical value of SIF; $L_r={\sigma }_{ref}/{\sigma }_T$ is a parameter determining the tough fracture mechanism (plastic instability) for the crack; ${\sigma }_T$ is the yield strength; $k$ is the permissible safety factor regulated by regulatory documents.

Consider the case when an annular outer surface semi-elliptical crack with semi-axes $a$ and $c$ is located in the vicinity of weld seam. The thickness of the pipe is denoted by $t$, and depth of the defect is denoted by $a$.

Analytical formulas for calculating the safety factors (SF) $n$ of a pipe segment with a crack were obtained in [2, 3, 14], taking into account residual stresses. In this case, depending on the value of $n$, according to regulatory documents, the defect belongs to a certain category of damage (minor, moderate, significant, critical) and the possibility of further operation or the term of repair of the damaged segment of the shell structure is established.

To study the effect of residual stresses on the strength of a pipeline with a defect, it is expedient to use the concept of the coefficient of influence onto the pipeline safety margin, which is calculated as follows:

where $n_r$ and $n$ are the values of the safety factors of the pipeline with a defect under the action of residual stresses and outside the welded joint, respectively.

Such a coefficient makes it possible to analyze the influence of the character of residual weld stresses in the presence of pipe surface defects. It is known [2, 3, 15] that for a welded pipe joint, axial stresses can have a different character depending on the pipe surface: they are compressive at the outer surface and tensile at the inner surface, respectively. In the case of high-strength steels, it is typical that areas with uneven (unlike in low-alloyed steels) stress distribution are formed in the vicinity of the weld. It mainly depends on the welding materials, conditions of the process, steel alloying characteristics, etc.

4. Research results

For our study, pipe joints made of high-strength steels with a diameter of 1020 mm and a wall thickness of 12 mm were selected. The physical and mechanical characteristics of the steel are the following: $E=$2.1×10⁵ MPa, $\mu =\text{0.3}$, ${\sigma }_b=\text{760}$ MPa, ${\sigma }_{0.2}=\text{690}$ MPa [16]. The internal pressure of the transported product was 6.0 MPa. The static strength of welds at pipe joints with defects in annular welds was studied. This is due to the peculiarities of production of such joints: mainly in the construction site using the manual arc method. In this case, the probability of a defect occurring increase as compared to factory conditions of production.

In the case of studying the strength of a pipeline with an defect located in the vicinity of a weld, it is important to take into account the axial weld stresses (${\sigma }_{\alpha \alpha }$) acting upon the defect. The distribution of residual weld stresses was assumed to be typical for the case of using bainite-ferrite and austenitic welds in welding high-strength steel plates [11]. In both cases, tensile stresses were observed at the outer surface, but for bainite-ferrite welds there is a slight decrease in stresses in the vicinity of the weld axis. When welding high-strength steels with austenitic welds, tensile stresses are higher, but the distribution is flatter. At the same time, work [11] shows that the welding method used and process regime have a significant influence.

Below (Fig. 1), we show the distribution of residual axial stresses at the inner and outer surfaces of walls of the pipe at the following values of the functions for describing residual plastic deformations: $b_1=\text{14}$; $b_2=\text{10}$; $b_3=\text{8}$; $s_1=\text{1}$; $s_2=\text{2}$; $s_3=\text{1}$; ${\rho }_0=\text{0}$; ${\rho }_3=\text{0.6}$; $q_1=\text{0.25}$; $q_2=\text{0.3}$; $\phi =\text{0}$. The following parameter values were also adopted: $n_1=\text{0.5}$; $n_2=\text{0.125}$ to illustrate the peculiarities of using austenitic (1, 3 – Fig. 1) and bainite-ferrite (2, 4 – Fig. 1) welds. This made it possible to obtain such changes in residual stresses in the vicinity of the weld axis which are typical of these kinds of welds.

Fig. 1Distribution of residual weld axial stresses in a welded pipe joint: 1, 2 – inner surface; and 3, 4 – outer surface of the joint

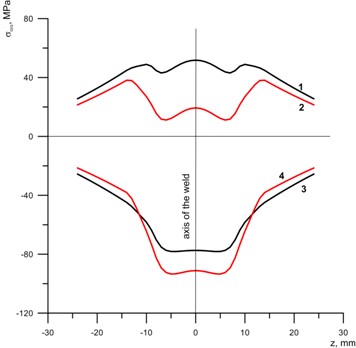
The character of the stresses indicates an uneven distribution of axial stresses over the thickness with an almost antisymmetric distribution in pairs of the corresponding curves concerning the inner and outer surfaces of the pipe. At the inner surface of the pipe, these stresses are tensile in both cases. At the outer surface, the axial stresses are compressive for both kinds of welds. These stresses gradually decrease with distance from the weld axis. The greatest changes occur at a distance of approximately 14 mm from the weld axis, which corresponds to the maximum size ($b_1$) of the plastic deformation zone. In general, it should be noted that the presented pattern of changes in residual stresses depending on the kinds of weld is primarily due to the peculiarities of thermo-deformation processes during cooling and crystallization of the welded joint metal [4, 5, 11].

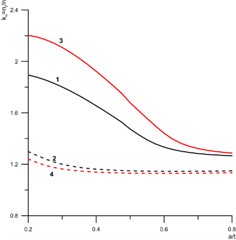
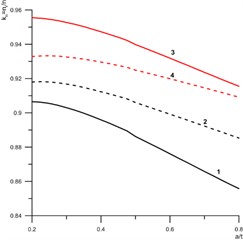
The effect of residual stresses on the strength of a welded joint (Eq. (3)) with a defect is shown in Fig. 2 for the case of the outer (a) and inner (b) surfaces of the welded pipe joint. The obtained dependencies take into account the aforesaid distributions of residual stresses for different kinds of welds when a defect is located on the weld axis, and when a defect is located at a certain distance from the axis (14 mm).

In all the cases, an increase in the relative depth of the defect ($a/t$) leads to a decrease in the safety factor of the welded pipe joint. However, the character of the stresses (tension/compression) should be taken in to account: tension creates different effect on the value of the $k_n$ factor than compression does.

Fig. 2Dependence of the coefficient of influence of residual stresses upon the safety factor (kn) of the pipeline on the relative depth of the defect: a) outer surface; b) inner surface; solid lines – nr/n values for the defect on the weld axis; dashed lines – nr/n values for the defect at a distance from the weld axis; 1, 2 – austenitic structure of the weld; 3, 4 – bainite-ferrite structure of the weld

a)

b)

The compressive residual welding stresses at the outer surface of the pipe in their directions are opposite to the operational tensile stresses caused by to internal pressure. Therefore, in this case these stresses contribute to an increase in the safety factor. Accordingly, for defects located at the outer surface of the joint the value of the influence factor $k_n$ is particularly high at the weld axis. This is where the compressive stresses caused by the welding cycle reach their maximum. The influence factor $k_n$ is higher for welds with a bainite-ferrite structure (curve 3 in Fig. 2(a)), because the compressive stresses in this case are the highest. For welds with an austenitic structure, this effect is less (curve 1 in Fig. 2(a)). With the distance from the weld axis, the compressive stresses decrease and are similar for both kinds of welds. Therefore, the influence factors $k_n$ are also significantly lower for both kinds of welds (curves 2, 4 in Fig. 1(a)). At the same time, the higher values of compressive stresses for austenitic welds at a distance of 14 mm ensure a slightly higher $k_n$ factor (curve 2 in Fig. 1(a)) as compared to bainite-ferrite welds (curve 4 in Fig. 1(a)).

At the inner surface of the pipe joint, the residual weld stresses are tensile (curves 1, 2 in Fig. 1). That is, the stresses here have a harmful influence on the safety margin of the pipeline, and therefore all $k_n$ values are less than unity (Fig. 2(b)). In this case, austenitic welds lead to the highest values of tensile stresses on the weld axis (curve 1 in Fig. 2(b)). Accordingly, the resulting values of the influence factor are the smallest. Similarly, the bainite-ferrite structure of the weld leads to a local decrease in tensile weld stresses on the weld axis. As a result, the influence factor for such welds is significantly higher (curve 3 in Fig. 2(b)). At the distance from the weld axis (14 mm) specified above, the axial weld stresses take intermediate values between the maximum and minimum values for both kinds of welds (Fig. 1). Therefore, the coefficients of influence of these stresses upon the pipeline safety factor ($k_n$) similarly takes an intermediate value (curves 2, 4 in Fig. 2(b)). The stresses in the austenitic weld have a slightly greater influence (curve 2 in Fig. 2(b)) and for the bainite-ferrite weld lesser influence (curve 4 in Fig. 2(b)). In both cases, an increase in the relative depth of the defect leads to a decrease in the value of the coefficient of influence of weld axial stresses.

5. Conclusions

The results obtained show that the complicated character of axial stresses in the welded joint of pipes caused by the action of the welding cycle can have different influences on the safety factor of the pipeline as a whole. In particular, compressive weld stresses at the outer surface of the pipe increase the safety factor of the pipeline. Similarly, tensile weld stresses on the inner surface of the pipe significantly reduce the safety factor.

The presence of low-temperature structural transformations in a welded joint can significantly affect the character of residual weld stresses, and as a result, affect the safety factor of the welded joint.

As the relative depth of the surface defect increases, the coefficient of influence of weld axial stresses decreases.