Analysis of the natural characteristics of fiber-reinforced cantilever beams using 8-node solid elements

Li, Huadong; Liu, Jingjun

doi:10.21595/jve.2025.24678

Journal of Vibroengineering

Browse Journal

Submit article

Published: 08 June 2025

Check for updates

Analysis of the natural characteristics of fiber-reinforced cantilever beams using 8-node solid elements

Huadong Li¹

Jingjun Liu²

^{1, 2}Jinlin Songhuajiang Thermoelectricity Co., Ltd., China

Corresponding Author:

Huadong Li

Cite the article Download PDF

Article in Press

Downloads 81

Abstract

A combined theoretical and experimental approach is employed to investigate the dynamic characteristics of fiber-reinforced cantilever beams. An 8-node element method establishes the theoretical model of the cantilever beam, allowing for the determination of its dynamic properties. A relevant experimental platform is constructed to test the fiber-reinforced cantilever beams, thereby validating the accuracy of the theoretical model. The results indicate that the theoretical model accurately predicts the dynamic characteristics of fiber-reinforced cantilever beams. Finally, based on the established theoretical model, the effects of cantilever beam length, width, and elastic modulus on the dynamic characteristics of the cantilever beam are discussed.

1. Introduction

A beam is an elongated component that primarily resists loads through bending. It is widely used in industries such as construction, aviation, automotive, and power generation [1-3]. These beams are fabricated into structures like propeller blades and aircraft wings and are frequently subjected to dynamic loads. To prevent damage due to vibrations from affecting the normal operation of equipment, it is essential to analyze the dynamic characteristics of these structures. Therefore, this paper analyzes the dynamic characteristics of a cantilever beam based on the 8-node solid element method and validates the correctness of the proposed theoretical model through experiments.

Both domestic and international researchers have conducted extensive studies on the static and dynamic characteristics of cantilever beams. Some scholars have analyzed the static characteristics of cantilever beams, such as Beléndez et al. [4] studied the deflection problem of a cantilever beam made of linear elastic material under an external concentrated load at the free end. Zhang et al. [5] developed an analysis model for surface stress on rectangular cantilever beams and compared the calculation results of three models under three different loading conditions. Girhammar et al. [6] investigated the general loading and boundary conditions of uniformly distributed composite beams and beam columns with interlayer slips. Liao et al. [7] proposed an improved Oberst beam technique to calculate the complex Young's modulus of non-rigid materials, enhancing measurement accuracy.

In addition to the static characteristic analysis of cantilever beams, it is also essential to analyze their dynamic characteristics. In recent years, both domestic and international scholars have conducted numerous studies on the dynamic characteristics of cantilever beams using a variety of theoretical methods, including higher-order theories, finite element methods, and others. Research has been carried out on the nonlinear vibration, rotating cantilever beams, damping in cantilever beams, and cantilever beams with fatigue cracks. The following scholars have conducted systematic studies on the free vibration of cantilever beams: Zhou et al. [8] used the Rayleigh-Ritz method to study the vibration characteristics of tapered beams with continuously varying rectangular cross-sections. Vu et al. [9] proposed an exact method for solving the vibration of double-beam systems under harmonic excitation, explaining the principles of the vibration problem and discovering that each natural mode consists of two sub-modes. Banerjee et al. [10] conducted a free vibration analysis of three-layer symmetric sandwich beams using the dynamic stiffness method. Zheng et al. [11] used the finite element method to solve the natural frequencies and mode shapes of cracked beams. Compared to analytical results, this method provided a more accurate stiffness matrix and more precise natural frequencies. Orhan et al. [12] studied the free and forced vibration of cracked cantilever beams, finding that the changes in natural frequencies were minimally affected by variations in crack depth and location. Yang et al. [13] derived the in-plane free vibration and governing differential equations for curved and non-uniformly curved beams using the extended Hamiltonian principle, accurately calculating the free vibration of curved beams. Jaworski et al. [14] analyzed the unbent vibration of multi-sectional stepped cantilever beams using beam theory methods, discussing the convergence of several theoretical methods. Alshorbagy et al. [15] investigated the dynamic characteristics of functionally graded beams with mate-rial gradients along the thickness and axial directions. This model was discretized using the finite element method to obtain a numerical approximation of the equations of motion. The method was validated against previous research results and showed good agreement.

Some scholars also used higher-order theories to analyze the vibration characteristics of cantilever beams. For example, Kant [16] and Thai [17] analyzed the dynamic characteristics of beams using first-order shear deformation theory and higher-order shear deformation theory, respectively.

Additionally, some scholars have researched the engineering applications related to beams. For example, Li et al. [18] proposed an analytical method for calculating the natural characteristics of shell plate blades, solving their natural frequencies and responses using the cantilever beam approach to facilitate subsequent fatigue life calculations. Guan et al. [19] studied the nonlinear vibration response of edge cracks and surface cracks in compressor blades, finding that edge cracks pose a greater danger than surface cracks.

In recent years, both domestic and international scholars have conducted research on various other characteristics of cantilever beams, such as their nonlinear vibration characteristics, the impact of boundary conditions on vibrations, and damping properties. For example, Ni et al. [20] proposed a method for predicting the dynamic performance of laminated composite beams, using Tsai's plate theory to predict damping behavior. Shang-Rou et al. [21] considered the nonlinear normal modes of finite amplitude vibrations in cantilever beams. Hilal et al. [22] explored the vibration problems of homogeneous isotropic beams under moving loads with general boundary conditions, examining the effects of parameter variations on beam responses. Sedighi et al. [23] obtained the vibration equations for highly nonlinear cantilever beams with dead zone nonlinear boundary conditions using He's parameter expansion method. Chung et al. [24] performed finite element analysis on rotating cantilever beams, deriving three linear partial differential equations using the Hamiltonian principle. They ultimately determined the effect of rotational speed distribution on the vibration characteristics of the beam. Brancheriau et al. [25] improved the accuracy of theoretical models by analyzing the longitudinal vibration of prismatic beams of various geometric types through self-vibration analysis. Delgado Velázquez et al. [26] investigated the vibration problems of highly flexible cantilever beams, calculating large steady-state and transient responses using the NLB program. Şimşek et al. [27] studied the vibration problems of functionally graded simply supported beams under moving mass using the third-order shear deformation theory. Raj et al. [28] conducted a dynamic analysis of multi-degree-of-freedom beams, modeling cantilever beams using ANSYS and MATLAB software to obtain the system’s frequency response functions. Dong et al. [29] analyzed the natural frequencies and vibration modes of continuous beams under free modes, axial tension, and axial compression based on Ray-leigh’s theory, validating the method's reasonableness through ANSYS. Wang et al. [30] examined the effects of various crack parameters, such as crack depth, crack location, and plate length, on the vibration characteristics of cracked plates through simulation and experimentation. Other scholars have conducted extensive reviews on functionally graded materials and various fiber-reinforced shell materials, such as: Asadi Jafari et al. [31] analyzed the classical, shear deformation, and three-dimensional theories. They discussed the characteristics of different material types, including composites, isotropic materials, and functionally graded materials, as well as the properties of sandwich plate structures, organized by boundary conditions. The importance of the type of incident field was also examined. The research methods were evaluated, and relevant papers were classified based on the optimization and control programs for sound propagation, providing valuable references for future research. Talebitooti et al. [32] studied the acoustic field characteristics of porous material sandwich composites, with a focus on the impact of the porous core on sound transmission loss (STL). They employed Biot's theory and the shear deformation shallow shell theory to model the wave propagation characteristics in composites and determined the critical angle of incidence. The results were compared with those in the literature, validating their accuracy, emphasizing the importance of porous materials, and assessing the sound insulation performance of the composites. Zarastvand et al. [33, 34] classified shells with different geometries and explored the application of classical theory, shear deformation theory, and three-dimensional theory in acoustic modeling. They emphasized the importance of material properties in modeling and analyzed the effects of different boundary conditions and external environments (such as fluids and heat). The paper also investigated the impact of incident field types on sound insulation performance and discussed control and optimization techniques to improve the acoustic behavior of shell structures. In the context of plate structures, over 200 relevant studies were reviewed, the research outcomes were classified, and the role of different theories in structural acoustic performance was highlighted. Additionally, the characteristics of material types and sandwich plate structures were discussed, and the significance of boundary conditions and incident field types was examined.

In summary, current research on the vibration characteristics of cantilever beams mainly relies on software or traditional numerical analysis methods, which are unable to accurately solve for their natural characteristics. However, traditional numerical methods have significant limitations, including strict constraints related to the assumed conditions. Furthermore, previous studies have seldom addressed the vibration characteristics of fiber-reinforced cantilever beams made from carbon fiber-reinforced composites. At present, fiber-reinforced composites are widely used across various industries, particularly with the rapid development of carbon fibers, which are extensively applied due to their excellent mechanical properties. Additionally, cantilever beam structures are considered fundamental structures in various systems and possess significant research value. Therefore, this paper employs an 8-node element method based on laminated plate theory to calculate the natural characteristics of fiber-reinforced cantilever beams. Experimental validation is conducted to verify the accuracy of the theoretical model presented in this paper. Finally, the influence of different parameters on the dynamic characteristics of the cantilever beam is discussed, providing important reference value for the practical engineering application of cantilever beams.

2. Dynamic modeling of cantilever beams based on solid elements

This chapter establishes a theoretical model of a cantilever beam using the finite element nodal method and solves for the vibrational characteristics of the cantilever beam. The finite element method and other elastic theories cannot accurately determine the stress-strain relationship of the structure. However, by using different elastic constants, we can obtain stress-strain coefficients in different directions and establish constitutive relationships to solve for the natural frequency using the energy method.

2.1. Dynamic model of cantilever beams

An 8-node solid element is used to establish the finite element model of the cantilever beam. The geometric model of the cantilever beam is shown in Fig. 1, where the length of the cantilever beam is denoted as $L$ . The global coordinate system is represented as $O X Y Z$ . The cantilever beam is subjected to a base excitation $F$ , oriented as illustrated in Fig. 1. The figure also depicts the loading conditions for each solid element, with the coordinate system for a single solid element shown as well.

Fig. 1Dynamics model of cantilever beam

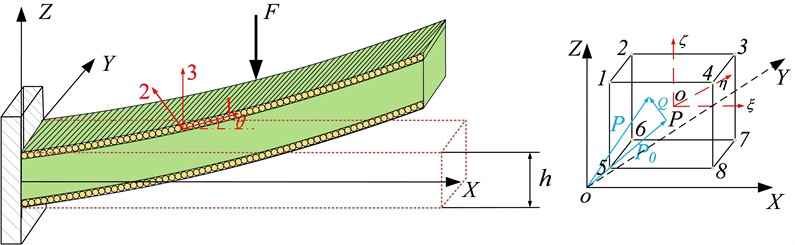
Let the position of an arbitrary point P on the nodal element be denoted as $P_{0}$ . The expressions for the initial position and instantaneous position are given as follows:

1

P_{0} = {[x_{0}, y_{0}, z_{0}]}^{T}, P = {[x_{0} + u, y_{0} + v, z_{0} + w]}^{T} .

The displacement matrix $A$ at any point of the cantilever beam can be expressed as:

2

A = [\begin{array}{l} u \\ v \\ w \end{array}] .

The element kinetic energy $T_{e}$ can be represented in terms of the displacement matrix $A$ as follows:

3

T_{e} = \frac{1}{2} \underset{e}{∭} ρ {\dot{A}}^{T} \dot{A} d V .

The dot above the symbol indicates a derivative concerning time.

The displacement function of the cantilever beam is given by:

4

\{\begin{array}{l} u = \sum_{i = 1}^{8} N_{i} (ξ, ζ, η) u_{i} + \sum_{j = 1}^{3} P_{j} α_{j}, \\ v = \sum_{i = 1}^{8} N_{i} (ξ, ζ, η) v_{i} + \sum_{j = 1}^{3} P_{j} β_{j}, \\ w = \sum_{i = 1}^{8} N_{i} (ξ, ζ, η) w_{i} + \sum_{j = 1}^{3} P_{j} γ_{j}, \end{array}

where, $u_{i}$ , $v_{i}$ , and $w_{i}$ represent the displacements of the nodal element in the $x$ , $y$ , and $z$ directions, respectively. $α_{j}$ , $β_{j}$ , and $γ_{j}$ denote the incompatible displacements within the element. $P_{j}$ represents the incompatible displacement function within the element, which is expressed as follows:

5

\{\begin{array}{l} P_{1} = 1 - ξ^{2}, \\ P_{2} = 1 - ζ^{2}, \\ P_{3} = 1 - η^{2} . \end{array}

Based on the 8-node solid element method, the shape function formula for the cantilever beam is obtained, where the matrix $N$ is given by:

6

N = [N_{1} N_{2} N_{3} N_{4} N_{5} N_{6} N_{7} N_{8}],

where, $N_{i}$ can be expressed as:

7

N_{i} = [\begin{array}{l} N_{i} & 0 & 0 \\ 0 & N_{i} & 0 \\ 0 & 0 & N_{i} \end{array}],

N_{i} = \frac{1}{8} (1 + ξ_{i} ξ) (1 + ζ_{i} ζ) (1 + η_{i} η),

where, $ξ$ , $ζ$ , and $η$ represent the nodal coordinates in the $x$ , $y$ , and $z$ directions, respectively.

The relationship between the stress and strain of the cantilever beam element and the element shape functions is given by:

8

[\begin{array}{l} \frac{\partial N_{i}}{\partial x} \\ \frac{\partial N_{i}}{\partial y} \\ \frac{\partial N_{i}}{\partial z} \end{array}] = {[\begin{array}{l} \frac{\partial x}{ξ} & \frac{\partial y}{ξ} & \frac{\partial z}{ξ} \\ \frac{\partial x}{ζ} & \frac{\partial y}{ζ} & \frac{\partial z}{ζ} \\ \frac{\partial x}{η} & \frac{\partial y}{η} & \frac{\partial z}{η} \end{array}]}^{- 1} [\begin{array}{l} \frac{\partial N_{i}}{\partial ξ} \\ \frac{\partial N_{i}}{\partial ζ} \\ \frac{\partial N_{i}}{\partial η} \end{array}] .

The transformation matrix in the above equation is the Jacobian matrix, which can be expressed in matrix form as follows:

9

J = [\begin{array}{l} \frac{\partial x}{ξ} & \frac{\partial y}{ξ} & \frac{\partial z}{ξ} \\ \frac{\partial x}{ζ} & \frac{\partial y}{ζ} & \frac{\partial z}{ζ} \\ \frac{\partial x}{η} & \frac{\partial y}{η} & \frac{\partial z}{η} \end{array}] .

The element stiffness matrix, element mass matrix and element damping matrix of the structure are as follows:

10

\begin{array}{l} M^{'} = \underset{e}{∭} ρ N^{T} N |J| d ξ d ζ d η, \\ C^{'} = \underset{e}{∭} μ N^{T} N d ξ d ζ d η, \\ K^{'} = \underset{e}{∭} B^{T} D B |J| d ξ d ζ d η, \end{array}

where, $B$ is the geometric matrix of the whole structure, and $D$ is the elastic matrix.

Substituting Eq. (4), Eq. (5), and Eq. (7) into Eq. (3) yields the kinetic energy of the element nodes:

11

T_{e} = \frac{1}{2} {\dot{δ}}^{e}^{T} \underset{e}{∭} ρ N^{T} N d V {\dot{δ}}^{e},

where, $δ^{e}$ denotes the displacement vector of the element nodes, which is expressed in the following form:

12

δ^{e} = {[u_{1}, v_{1}, w_{1}, \dots, u_{8}, v_{8}, w_{8}]}^{T} .

According to the Lagrangian function, the equation is obtained as follows:

13

\frac{d}{d t} (\frac{\partial T}{\partial \dot{δ}}) - \frac{\partial T}{\partial δ} + \frac{\partial V}{\partial δ} = F,

where, $F$ represents the generalized displacement vector.

Combining the element stiffness matrix, mass matrix and vector $F$ , the vibration equation for solving the eigenvalue problem can be obtained through the differential equation of motion of the cantilever beam, where the differential equation of motion is:

14

M \ddot{δ} + C \dot{δ} + K δ = F,

where, $M$ , $C$ , and $K$ represent the complete mass matrix, damping matrix, and stiff-ness matrix, respectively.

Based on the differential equation of cantilever beam vibrations, solving the eigen-value problem yields the natural frequency $ω$ and the mode shapes of the cantilever beam:

15

(K - ω^{2} M) q = 0 .

Stiffness matrix and mass matrix construct characteristic equation. For eigenvalue problems, we need to set part of the stiffness matrix to 0, so the natural frequency of the structure can be solved.

Through the above theoretical description, we can calculate the stiffness matrix and mass matrix of the structure through the stress-strain relationship. The natural frequency of the structure is calculated by Matlab to predict the vibration characteristics of the structure.

To sum up, the establishment of the theoretical model can predict the natural frequency of the fiber reinforced cantilever beam, and the correctness of the theoretical model can be determined by setting up an experimental platform to verify the natural frequency of the structure.

Finally, because the thickness of the fiber beam is small, the shear deformation has little influence on the natural frequency of the whole structure. Therefore, we ignore the influence of shear deformation theory on it.

2.2. Validation of the dynamic model for cantilever beams

This chapter primarily validates the accuracy of the theoretical model proposed in this study through experimental methods. The main content includes the establishment of the experimental testing platform and the experimental testing process, along with the comparison and verification of results. The experiments provide evidence to support the accuracy of the theoretical model presented in this study.

2.3. Construction of the experimental testing platform and testing procedure

This section primarily introduces the construction of the experimental test platform and the experimental procedures. Fig. 2 shows the setup of the test platform, where the experimental specimen is fixed on one side using a fixture and bolts, with a clamping length of 30 mm. The testing system mainly consists of an ECON MI-7004 data acquisition device, a PCB accelerometer, a SALC05KE modal hammer, and a laptop computer. During the experimental testing, the experimental cantilever beam is divided into ten equal segments along its length, with each measurement point correspondingly marked. The accelerometer is fixed at point 8, as shown in the figure. The carbon fiber reinforced cantilever beam has a fiber orientation of 0/90° unidirectional layup, with a total of 21 layers. The specific layering mode is 0° layering and 90° layering, the overall layering mode is 21 layers, and the first layer is 0° layering. Additionally, the cantilever beam specimen is a T300 carbon fiber reinforced cantilever beam. The reinforcing fiber is carbon fiber, and the matrix material is epoxy resin. The fiber reinforcement percentage ranges from approximately 55 % to 65 %, with carbon fiber comprising 60 % to 70 % and resin comprising 30 % to 40 %. Additionally, the angle between the fiber layers in the fiber-reinforced cantilever beam and the x-direction is either 0° or 90°.The material parameters for the cantilever beam include $E_{1}$ the Young's modulus along the fiber direction; $E_{2}$ , the Young’s modulus perpendicular to the fiber direction; $G_{12}$ , the shear modulus in the 12-direction; and $v_{12}$ , the Poisson's ratio in the 12-direction [35]. The specific values of the material and geometric parameters are provided in Table 1. It is worth noting that the beam is a layered structure, and the geometric parameters and material parameters of the beam in the table are the overall parameters of the beam structure.

Fig. 2Cantilever beam test site diagram

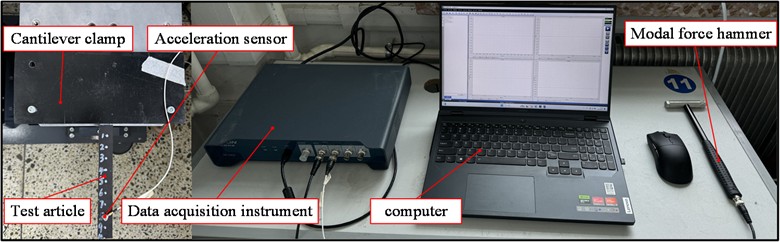
Table 1Cantilever beam related material parameters and geometric parameters

Type	Length (mm)	Width (mm)	Thickness (mm)	$E_{1}$ (GPa)	$E_{2}$ (GPa)	$G_{12}$ (GPa)	$v_{12}$	$ρ$ (kg/m³)
Carbon fiber beam	230	25	3	15	5	1.6	0.4	1600

During the testing process, a multi-point excitation and single-point response measurement method is employed. The modal hammer sequentially strikes each measurement point on the cantilever beam, while the sensor records the beam's vibration response after each impact. Upon completion of the sequential strikes, the data acquisition device analyzes the vibration data to generate the modal shapes of the cantilever beam.

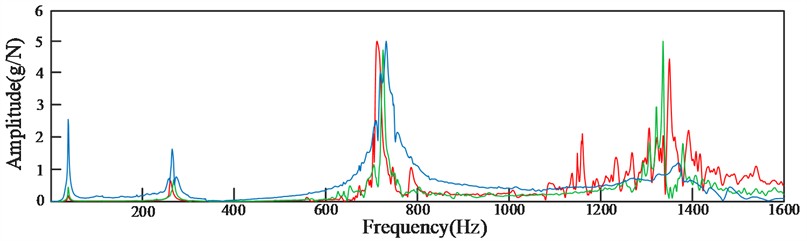
Additionally, the modal testing of the cantilever beam also determines its natural frequencies. When identifying the natural frequencies of the cantilever beam, the parameters of the experimental testing system are set as follows: (I) the testing bandwidth is set to 0-3000 Hz, (II) the resolution is 0.5 Hz, and (III) the window function applied is the Hanning window. To ensure the accuracy of the data, three valid tests are conducted at each measurement point. The three impact curves in the figure exhibit some discrepancies, and there are several potential reasons for these errors. For example, during the impact testing, the force hammer was manually held, which means that the force applied during each impact may not have been uniform, leading to certain variations. Additionally, during the impact process, the cantilever beam may have experienced slight vibrations, or external vibrations and noise in the environment could have affected the results. Despite these factors, the resonance frequencies generated by the three impacts are essentially the same, and the peak positions also coincide. Therefore, these results can be considered as the natural frequency of the cantilever beam. Furthermore, the coherence of the impacts is assessed to determine whether the data is representative, with only those experimental data exhibiting good coherence being retained.

The natural frequency curve of the cantilever beam obtained from the impact tests is shown in Fig. 3.

Fig. 3Frequency response diagram of three experimental knocks of a cantilever beam

2.4. Construction of the experimental testing platform and testing procedure

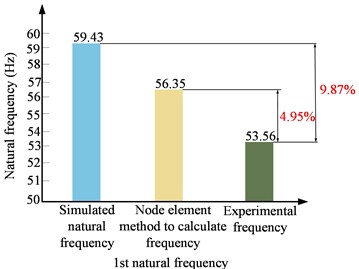
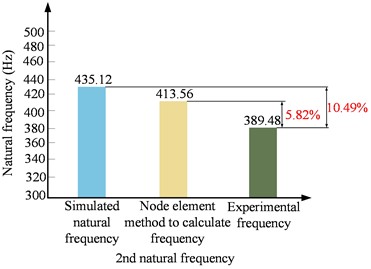
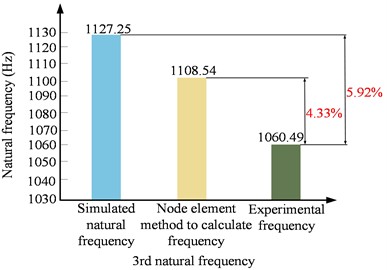
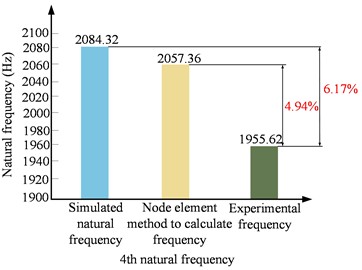
This section primarily discusses and analyzes the experimental results, comparing them with theoretical calculations to determine the accuracy of the theoretical model proposed in this study. To validate the accuracy of the theoretical model, the natural frequencies calculated using the 8-node finite element method are compared with the simulation results and the experimental results of the first four natural frequencies of the cantilever beam. The corresponding error parameters are provided. Additionally, the first four mode shapes obtained from theoretical calculations are compared with the experimental test results, as shown in Table 2. Further-more, Fig. 4 presents the errors between the simulation frequencies, the frequencies calculated by the model in this paper, and the experimental frequencies.

Table 2Comparison of experimental and theoretical calculated natural frequencies and mode shapes

Mode	Simulated natural frequency (Hz)	Node element method to calculate frequency (Hz)	Experimental frequency (Hz)	Error (%)	Modal calculation by nodal element method	Experimental mode
1	59.43	56.35	53.56	4.95
2	435.12	413.56	389.48	5.82
3	1127.25	1108.54	1060.49	4.33
4	2084.32	2057.36	1955.62	4.94

As shown in Table 2, the errors between the first four natural frequencies of the cantilever beam obtained using the 8-node finite element method and the experimental natural frequencies are less than 5.82 %. Compared to the experimental natural frequencies, these errors are significantly smaller than those calculated using the simulation method for the first four natural frequencies of the cantilever beam.

Additionally, it is necessary to explain the observed differences between the theoretical calculations and the experimental results, as these discrepancies may be attributed to various factors. Firstly, the specimen is a fiber-reinforced composite cantilever beam, characterized by material nonlinearity and geometric nonlinearity; the interplay of these two factors may contribute to experimental errors. However, since the experimental method employs a modal hammer for multi-point excitation and single-point response, rather than using a shaker table or a continuously exciting exciter, it is challenging to determine whether the observed effects are due to material nonlinearity or geometric nonlinearity. Nonetheless, the influence of these two factors on the experimental results must be considered.

Fig. 4Comparison of calculation frequency and experimental frequency with different calculation methods

Furthermore, other sources of error may also exist. For instance, as the mode order increases, the vibrational response of the cantilever beam diminishes, and slight environmental changes can significantly affect the experimental outcomes. Additionally, during the experimentation process, the results may be influenced by various factors such as temperature fluctuations, air damping, and sensor calibration errors. The computational method employed in this study does not account for the effects of inter-laminar friction, the discrete effects of composite materials, or the influence of residual stresses. Therefore, these factors may contribute to discrepancies in the theoretical calculations. Considering all the aforementioned factors, the errors and fluctuations observed in the theoretical calculations remain within a reasonable range. Consequently, the theoretical model presented in this study can accurately predict the dynamic characteristics of the cantilever beam.

2.5. Impact of varying parameters on the dynamic characteristics of cantilever beams

This chapter discusses the influence of different material and geometric parameters on the dynamic characteristics of the cantilever beam. Since the theoretical model proposed in this study has been validated in the preceding sections, this chapter investigates the effects of varying the relevant parameters of the cantilever beam on its dynamic characteristics through theoretical calculations. The aim is to explore how different structural configurations impact the dynamic behavior of the cantilever beam. In addition, the theoretical calculation results in this chapter are calculated based on the theoretical model. We use Matlab software to calculate the stress-strain and stiffness mass matrix to obtain the natural frequency of the structure. By changing the structural parameters, the natural frequency of the structure can be obtained by changing the material parameters and the structural parameters entered in the program.

2.6. Effect of varying lengths on the dynamic characteristics of cantilever beams

This section primarily discusses the impact of cantilever beam length on its dynamic characteristics. To ensure the reliability of the discussions in this section while varying the length of the cantilever beam, we keep all other parameters constant, including both geometric and material parameters. For example, parameters such as the number of layers in the composite cantilever beam, the width of the cantilever beam, as well as the elastic modulus and shear modulus are maintained unchanged. Table 3 presents the effects of different cantilever beam lengths on the dynamic characteristics of the cantilever beam.

Table 3Natural frequencies of cantilever beams at varying lengths

Mode	150 mm	200 mm	250 mm
1	71.21	56.35	40.25
2	497.36	413.56	340.21
3	1321.15	1108.54	982.35
4	2421.65	2057.36	1752.65

As shown in Table 3, when the length of the cantilever beam increases from 150 mm to 250 mm while keeping other parameters constant, the first natural frequency of the cantilever beam decreases from 71.21 Hz to 40.25 Hz. This phenomenon occurs because, as the length of the cantilever beam increases, the stiffness matrix $K$ in Eq. (15) decreases. Concurrently, the increase in length also causes the mass matrix $M$ , to increase, further contributing to the decrease in natural frequency. The stiffness matrix and mass matrix will have an impact on the natural frequency, and the reduction of the stiffness matrix is mainly due to the change of the geometrical parameters or material parameters of the structure, and the change of the structural parameters leads to the change of the stress and strain of the structure finishing. Therefore, the change of stress and strain will affect the stiffness of the structure, and the stiffness has a great influence on the natural frequency of the whole structure. Similarly, the variation of structural parameters on the mass matrix will also affect the stress-strain and thus affect the natural frequency of the structure. In the following sections, changes in structural parameters have roughly the same effect on the excitation of the natural frequency. However, the change in natural frequency is primarily influenced by the stiffness. The variation in the length of the cantilever beam plays a dominant role in altering its structural stiffness, thus leading to the observed decrease in natural frequency.

2.7. Effect of varying widths on the dynamic characteristics of cantilever beams

This section discusses the effect of the width of the cantilever beam on its natural characteristics. Due to the constraints of the cantilever beam structure, the width-to-height ratio should not exceed six. To facilitate comparison with the previously discussed conditions, the length of the cantilever beam is fixed at 200 mm and the thickness at 3 mm. The width of the cantilever beam varies within the range of 20 mm to 30 mm. Within this range, we analyze cantilever beams of different widths, and the variations in their natural frequencies are presented in Table 4.

As shown in Table 4, taking the first four natural frequencies of the cantilever beam as examples, it is evident that the natural frequencies of the cantilever beam decrease with an increase in its width. When the width of the cantilever beam increases from 20 mm to 25 mm, and then to 30 mm, the first natural frequency decreases from 63.12 Hz to 56.35 Hz, and further to 50.47 Hz. This is because, when the length and height of the cantilever beam remain constant, an increase in width leads to a decrease in the stiffness matrix $K$ , thereby affecting the change in its natural frequencies. Of course, the change in natural frequencies can also be influenced by other factors, such as material nonlinearity and geometric nonlinearity of the composite materials. However, this study focuses solely on the variation of natural frequencies, thus the effects of material and geometric nonlinearities are disregarded.

Table 4Impact of width variations on the natural frequencies of cantilever beams

Mode	20 mm	25 mm	30 mm
1	63.12	56.35	50.47
2	461.02	413.56	365.23
3	1225.68	1108.54	1021.56
4	2275.23	2057.36	1798.36

2.8. Influence of elastic modulus on dynamic characteristics of cantilever beam

This section primarily discusses the impact of variations in the elastic modulus of the cantilever beam on its dynamic characteristics. In this theoretical discussion, it is acknowledged that both the elastic modulus and the shear modulus of the structure typically vary simultaneously. The main reason is that the methods for altering the elastic modulus of fiber-reinforced structures primarily involve changing the reinforcement ratio, fiber orientation, materials, or the matrix of the fibers. However, this paper primarily investigates the dynamic characteristics of fiber-reinforced cantilever beams, where changes in the natural frequency are more strongly related to variations in the elastic modulus rather than the shear modulus [36]. Therefore, this study mainly focuses on the effect of the elastic modulus on the changes in the natural frequency. However, this paper focuses on the impact of changes in the elastic modulus on the natural frequency of the structure, while preliminarily assuming that the shear modulus remains unchanged. Similar to the previous section, to ensure the reliability of the data, only the elastic modulus of the cantilever beam is modified, while all other parameters remain unchanged. The cantilever beam has a length of 200 mm, a width of 25 mm, and a thickness of 3mm. The detailed results are presented in Table 5.

Table 5Effect of elastic modulus on the natural frequencies of cantilever beams

Mode	10 GPa	15 GPa	20 GPa
1	40.52	56.35	70.32
2	302.54	413.56	534.54
3	812.59	1108.54	1412.38
4	1512.02	2057.36	2603.21

According to Table 5, taking the first four vibration characteristics of the cantilever beam as an example, the natural frequency of the cantilever beam increases with an increase in its elastic modulus. This phenomenon occurs because the elastic modulus is closely related to changes in the structural stiffness; an increase in the elastic modulus of the cantilever beam results in an increase in the stiffness matrix $K$ . The increase in the stiffness matrix directly affects the variation in the natural characteristics of the structure [35]. Therefore, it is evident that the increase in the stiffness matrix in this section leads to an enhancement of the natural characteristics of the cantilever beam. It can be concluded that when the elastic modulus of the cantilever beam increases, its natural characteristics also increase, establishing a positive correlation between the two.

3. Conclusions

This paper proposes a theoretical model for investigating the dynamic characteristics of fiber-reinforced composite cantilever beams. The model utilizes an 8-node finite element method to accurately determine the inherent properties of fiber-reinforced composite beams under cantilever conditions. The error range for the calculated natural frequencies is between 4.33 % and 5.82 %, which is within an acceptable accuracy range. Notably, a comparison between the 8-node finite element method and simulation results reveals that the simulation errors are significantly greater than those of the 8-node method. The proposed 8-node finite element method provides more precise calculations of the stiffness matrix, significantly reducing errors compared to conventional simulations and demonstrating a higher degree of agreement with experimental results. This underscores the advancement of the theoretical model proposed in this paper and provides strong evidence that the model can accurately predict the dynamic characteristics of fiber-reinforced composite cantilever beams. Furthermore, this paper draws several important conclusions:

1) As its natural frequency increases, the natural frequency of the cantilever beam decreases to varying degrees. This reduction occurs because the increase in length leads to a decrease in the stiffness matrix of the cantilever beam, resulting in a corresponding decline in the natural frequency. Hence, it is evident that changes in the length of the cantilever beam will induce variations in the natural frequency.

2) As the width of the cantilever beam increases, the natural frequency of the beam correspondingly decreases. This phenomenon occurs because the increase in beam width leads to a reduction in stiffness, theoretically reflected by a decrease in the stiffness matrix and an increase in the mass matrix, thereby resulting in changes in the natural frequency.

3) The natural frequency of fiber-reinforced composite cantilever beams is positively correlated with the elastic modulus; thus, an increase in the elastic modulus results in a rise in the natural frequency of the cantilever beam.

Through the aforementioned validation, the theoretical model proposed in this paper accurately predicts the dynamic characteristics of cantilever beams, demonstrating a higher precision than conventional numerical analysis methods. Additionally, this theoretical model exhibits universality, adapting to cantilever beams with varying structural and material parameters, thereby providing significant reference value for both academic research and engineering applications.

References

R. B. Abarcar and P. F. Cunniff, “The vibration of cantilever beams of fiber reinforced material,” Journal of Composite Materials, Vol. 6, No. 3, pp. 504–517, Jul. 1972, https://doi.org/10.1177/002199837200600306

Publisher
D. K. Rao, “Vibration of short sandwich beams,” Journal of Sound and Vibration, Vol. 52, No. 2, pp. 253–263, May 1977, https://doi.org/10.1016/0022-460x(77)90644-7

Publisher
S. Abrate, “Vibration of non-uniform rods and beams,” Journal of Sound and Vibration, Vol. 185, No. 4, pp. 703–716, Aug. 1995, https://doi.org/10.1006/jsvi.1995.0410

Publisher
T. Beléndez, C. Neipp, and A. Beléndez, “Large and small deflections of a cantilever beam,” European Journal of Physics, Vol. 23, No. 3, pp. 371–379, May 2002, https://doi.org/10.1088/0143-0807/23/3/317

Publisher
Y. Zhang, Q. Ren, and Y.-P. Zhao, “Modelling analysis of surface stress on a rectangular cantilever beam,” Journal of Physics D: Applied Physics, Vol. 37, No. 15, pp. 2140–2145, Aug. 2004, https://doi.org/10.1088/0022-3727/37/15/014

Publisher
U. A. Girhammar and D. H. Pan, “Exact static analysis of partially composite beams and beam-columns,” International Journal of Mechanical Sciences, Vol. 49, No. 2, pp. 239–255, Feb. 2007, https://doi.org/10.1016/j.ijmecsci.2006.07.005

Publisher
Y. Liao and V. Wells, “Estimation of complex Young’s modulus of non-stiff materials using a modified Oberst beam technique,” Journal of Sound and Vibration, Vol. 316, No. 1-5, pp. 87–100, Sep. 2008, https://doi.org/10.1016/j.jsv.2008.02.028

Publisher
D. Zhou and Y. K. Cheung, “The free vibration of a type of tapered beams,” Computer Methods in Applied Mechanics and Engineering, Vol. 188, No. 1-3, pp. 203–216, Jul. 2000, https://doi.org/10.1016/s0045-7825(99)00148-6

Publisher
H. V. Vu, A. M. Ordóñez, and B. H. Karnopp, “Vibration of a double-beam system,” Journal of Sound and Vibration, Vol. 229, No. 4, pp. 807–822, Jan. 2000, https://doi.org/10.1006/jsvi.1999.2528

Publisher
J. R. Banerjee, “Free vibration of sandwich beams using the dynamic stiffness method,” Computers and Structures, Vol. 81, No. 18-19, pp. 1915–1922, Aug. 2003, https://doi.org/10.1016/s0045-7949(03)00211-6

Publisher
D. Y. Zheng and N. J. Kessissoglou, “Free vibration analysis of a cracked beam by finite element method,” Journal of Sound and Vibration, Vol. 273, No. 3, pp. 457–475, Jun. 2004, https://doi.org/10.1016/s0022-460x(03)00504-2

Publisher
S. Orhan, “Analysis of free and forced vibration of a cracked cantilever beam,” NDT and E International, Vol. 40, No. 6, pp. 443–450, Sep. 2007, https://doi.org/10.1016/j.ndteint.2007.01.010

Publisher
F. Yang, R. Sedaghati, and E. Esmailzadeh, “Free in-plane vibration of general curved beams using finite element method,” Journal of Sound and Vibration, Vol. 318, No. 4-5, pp. 850–867, Dec. 2008, https://doi.org/10.1016/j.jsv.2008.04.041

Publisher
J. W. Jaworski and E. H. Dowell, “Free vibration of a cantilevered beam with multiple steps: Comparison of several theoretical methods with experiment,” Journal of Sound and Vibration, Vol. 312, No. 4-5, pp. 713–725, May 2008, https://doi.org/10.1016/j.jsv.2007.11.010

Publisher
A. E. Alshorbagy, M. A. Eltaher, and F. F. Mahmoud, “Free vibration characteristics of a functionally graded beam by finite element method,” Applied Mathematical Modelling, Vol. 35, No. 1, pp. 412–425, Jan. 2011, https://doi.org/10.1016/j.apm.2010.07.006

Publisher
T. Kant and A. Gupta, “A finite element model for a higher-order shear-deformable beam theory,” Journal of Sound and Vibration, Vol. 125, No. 2, pp. 193–202, Sep. 1988, https://doi.org/10.1016/0022-460x(88)90278-7

Publisher
H.-T. Thai and T. P. Vo, “Bending and free vibration of functionally graded beams using various higher-order shear deformation beam theories,” International Journal of Mechanical Sciences, Vol. 62, No. 1, pp. 57–66, Sep. 2012, https://doi.org/10.1016/j.ijmecsci.2012.05.014

Publisher
H.-Y. Li, L.-Y. Xie, and X.-H. Guo, “Natural characteristics of the cylindrical panel blade,” Journal of Northeastern University (Natural Science), Vol. 32, No. 11, p. 1627, 2011.

Search CrossRef
H. Guan et al., “Comparison of nonlinear vibration responses induced by edge crack and surface crack of compressor blades,” Mechanical Systems and Signal Processing, Vol. 216, p. 111465, Jul. 2024, https://doi.org/10.1016/j.ymssp.2024.111465

Publisher
R. G. Ni and R. D. Adams, “The damping and dynamic moduli of symmetric laminated composite beams-theoretical and experimental results,” Journal of Composite Materials, Vol. 18, No. 2, pp. 104–121, Mar. 1984, https://doi.org/10.1177/002199838401800202

Publisher
H. Shang-Rou, S. W. Shaw, and C. Pierre, “Normal modes for large amplitude vibration of a cantilever beam,” International Journal of Solids and Structures, Vol. 31, No. 14, pp. 1981–2014, Jul. 1994, https://doi.org/10.1016/0020-7683(94)90203-8

Publisher
M. A. Hilal and H. S. Zibdeh, “Vibration analysis of beams with general boundary conditions traversed by a moving force,” Journal of Sound and Vibration, Vol. 229, No. 2, pp. 377–388, Jan. 2000, https://doi.org/10.1006/jsvi.1999.2491

Publisher
H. M. Sedighi and K. H. Shirazi, “A new approach to analytical solution of cantilever beam vibration with nonlinear boundary condition,” Journal of Computational and Nonlinear Dynamics, Vol. 7, No. 3, p. 034502, Jul. 2012, https://doi.org/10.1115/1.4005924

Publisher
J. Chung and H. H. Yoo, “"Dynamic analysis of a rotating cantilever beam by using the finite element method,” Journal of Sound and Vibration, Vol. 249, No. 1, pp. 147–164, Jan. 2002, https://doi.org/10.1006/jsvi.2001.3856

Publisher
L. Brancheriau and H. Bailleres, “Natural vibration analysis of clear wooden beams: a theoretical review,” Wood Science and Technology, Vol. 36, No. 4, pp. 347–365, Aug. 2002, https://doi.org/10.1007/s00226-002-0143-7

Publisher
I. Delgado-Velázquez, “Nonlinear vibration of a cantilever beam,” Rochester Institute of Technology, 2007.

Search CrossRef
M. Şimşek, “Vibration analysis of a functionally graded beam under a moving mass by using different beam theories,” Composite Structures, Vol. 92, No. 4, pp. 904–917, Mar. 2010, https://doi.org/10.1016/j.compstruct.2009.09.030

Publisher
R. Raj, P. K. Sinha, and E. V. Prakash, “Modelling, simulation and analysis of cantilever beam of different material by finite element method, Ansys and Matlab,” Governing, Vol. 4, 2015.

Search CrossRef
M. Dong, K. Zhou, Q. Liu, and Z. Li, “Inherent characteristic analysis of continuous beam under axial force,” International Journal of Recent Engineering Science, Vol. 4, No. 2, pp. 39–43, 2017.

Search CrossRef
H. Wang, H. Ma, W. Wang, H. Guan, and Z. Wu, “Analysis and experimental verification of dynamic characteristics of cantilever plate with fatigue crack,” Engineering Failure Analysis, Vol. 157, p. 107918, Mar. 2024, https://doi.org/10.1016/j.engfailanal.2023.107918

Publisher
M. H. Asadi Jafari, M. Zarastvand, and J. Zhou, “Doubly curved truss core composite shell system for broadband diffuse acoustic insulation,” Journal of Vibration and Control, Vol. 30, No. 17-18, pp. 4035–4051, Oct. 2023, https://doi.org/10.1177/10775463231206229

Publisher
R. Talebitooti and M. R. Zarastvand, “The effect of nature of porous material on diffuse field acoustic transmission of the sandwich aerospace composite doubly curved shell,” Aerospace Science and Technology, Vol. 78, pp. 157–170, Jul. 2018, https://doi.org/10.1016/j.ast.2018.03.010

Publisher
M. R. Zarastvand, M. Ghassabi, and R. Talebitooti, “Acoustic insulation characteristics of shell structures: a review,” Archives of Computational Methods in Engineering, Vol. 28, No. 2, pp. 505–523, Dec. 2019, https://doi.org/10.1007/s11831-019-09387-z

Publisher
M. R. Zarastvand, M. Ghassabi, and R. Talebitooti, “A review approach for sound propagation prediction of plate constructions,” Archives of Computational Methods in Engineering, Vol. 28, No. 4, pp. 2817–2843, Aug. 2020, https://doi.org/10.1007/s11831-020-09482-6

Publisher
H. Li et al., “Nonlinear vibrations of all-composite sandwich plates with a hexagon honeycomb core: Theoretical and experimental investigations,” Composite Structures, Vol. 305, p. 116512, Feb. 2023, https://doi.org/10.1016/j.compstruct.2022.116512

Publisher
X. Zhuo et al., “Analysis of nonlinear vibration characteristics in all-composite honeycomb-core sandwich panel with material and geometric nonlinearity,” Nonlinear Dynamics, Vol. 113, No. 7, pp. 6009–6030, Dec. 2024, https://doi.org/10.1007/s11071-024-10716-6

Publisher

About this article

Received

20 November 2024

Accepted

23 April 2025

Published

08 June 2025

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/jve.2025.24678

Keywords

fiber reinforced

nodal element

dynamic characteristic

cantilever beam

Acknowledgements

The authors have not disclosed any funding.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Author Contributions

Huadong Li: conceptualization. Jingjun Liu: methodology.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Research article

2020 04 02

Finite element modelling and dynamic characteristic analysis of the human CTL-Spine

Shreyas Dayanand, B R Dhruva Kumar, Ankit Rao, Chandrashekara C V, Mantesh B Khot, Harshvardhan Shetty

Research article

2019 11 28

Vibration analysis of cantilever beam in time domain and frequency domain using Arduino platform

Chetan Reddy, Sucheth Shenoy, Ramesh S. Sharma

Research article

2019 04 25

The effect of a crack near the fixed end on the natural frequencies of a cantilever beam

Cristian Tufisi, Gilbert-Rainer Gillich, Alexandra Teodora Aman

Research article

2017 06 30

Resonance vibration of an optical fiber micro-cantilever using electro-thermal actuation

Mojtaba Komeili, Aydin Ahrabi, Carlo Menon

H. Li and J. Liu, “Analysis of the natural characteristics of fiber-reinforced cantilever beams using 8-node solid elements,” Journal of Vibroengineering, Vol. 27, No. 5, –13, Jun. 2025, https://doi.org/10.21595/jve.2025.24678

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2025.24678
UR  - https://doi.org/10.21595/jve.2025.24678
TI  - Analysis of the natural characteristics of fiber-reinforced cantilever beams using 8-node solid elements
T2  - Journal of Vibroengineering
AU  - Li, Huadong
AU  - Liu, Jingjun
PY  - 2025
DA  - 2025/06/08
PB  - Extrica
VL  - 27
IS  - 5
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

 @article{Li_2025, title={Analysis of the natural characteristics of fiber-reinforced cantilever beams using 8-node solid elements}, ISSN={2538-8460}, url={https://doi.org/10.21595/jve.2025.24678}, DOI={10.21595/jve.2025.24678}, journal={Journal of Vibroengineering}, publisher={JVE International Ltd.}, author={Li, Huadong and Liu, Jingjun}, year={2025}, month=jun }

Copy Bibtex

Copied to clipboard!

[1]H. Li and J. Liu, “Analysis of the natural characteristics of fiber-reinforced cantilever beams using 8-node solid elements,” Journal of Vibroengineering, Jun. 2025, doi: 10.21595/jve.2025.24678.

Copy IEEE

Copied to clipboard!

Li, Huadong, and Jingjun Liu. “Analysis of the Natural Characteristics of Fiber-Reinforced Cantilever Beams Using 8-Node Solid Elements.” Journal of Vibroengineering, June 8, 2025. https://doi.org/10.21595/jve.2025.24678.

Copy Chicago

Copied to clipboard!

Analysis of the natural characteristics of fiber-reinforced cantilever beams using 8-node solid elements

Abstract

1. Introduction

2. Dynamic modeling of cantilever beams based on solid elements

2.1. Dynamic model of cantilever beams

2.2. Validation of the dynamic model for cantilever beams

2.3. Construction of the experimental testing platform and testing procedure

2.4. Construction of the experimental testing platform and testing procedure

2.5. Impact of varying parameters on the dynamic characteristics of cantilever beams

2.6. Effect of varying lengths on the dynamic characteristics of cantilever beams

2.7. Effect of varying widths on the dynamic characteristics of cantilever beams

2.8. Influence of elastic modulus on dynamic characteristics of cantilever beam

3. Conclusions

References

About this article

Related Articles