Data analytics-based model for optimizing cationic retarder and acetic acid in polyacrylic yarn dyeing

1. Introduction

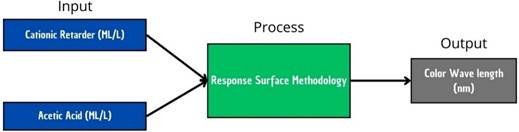
Many industries, including the textile industry, are utilizing mathematical approaches nowadays [1-4]. In textile products, dyeing is one of the most important processes that may determine the quality [5-7]. The dyeing process for textile polyacrylic yarns requires optimizing the concentration of cationic retarders and acetic acid to achieve the desired wavelength, which is a measure of color aging [8-10]. A mathematical model can be used to design an effective and efficient experiment regarding the optimization of two solutions' concentrations.

This optimization was carried out as an experimental design because if the wavelength produced is too large, it will produce a color intensity that is too bright. If the resulting wavelength is too small, the dyed color on the yarn will not be absorbed optimally, resulting in color fading when the yarn is applied to the fabric [11-13]. Therefore, it is necessary to develop a mathematical model that can optimize the wavelength based on the combined concentration of the two solutions to ensure the dyeing process is effective and efficient. The proposed mathematical model is the Response Surface Methodology (RSM) model. RSM is statistical modeling for designing experiments, understanding how independent and dependent variables relate, and optimizing experiments based on the number of experiments needed [14-16]. This study utilized the RSM model by exploring the possible nature of the relationship between the variables involved. The RSM model was validated by comparing it with actual data to determine its accuracy in making predictions.

As the coefficient of determination method shows, the RSM model maps the relationship between input and output variables by comparing the variation explained by the model to the variation in the data itself [17-19]. R-squared measures how much of the variation in the response can be explained by the model compared to the total variation. The higher the $R$-squared value, the better the RSM model is at explaining variation in the data [19].

Therefore, this study aims to design an experimental framework to find the optimal concentration of cationic retarders and acetic acid to achieve the desired wavelength for the yarn color aging test based on the description above. To support this objective, the study utilised secondary data obtained from a previously published experiment by [20], which explored the effects of cationic retarders and acetic acid concentrations in polyacrylic yarn dyeing. This dataset was selected because it comprehensively captures the relevant variables and experimental conditions necessary for RSM modelling. Its reliability and suitability enabled the development of an accurate mathematical model without the need for new experimental procedures, while still ensuring scientific validity and practical relevance. This model optimizes the yarn dyeing process using cationic retarders and acetic acid for the first time. Its novelty brings great expectations, especially for the textile industry, which utilizes this process as one of its major processes. Through this research, it is hoped that the effectiveness and efficiency of yarn dyeing can be improved, as well as a deeper understanding of the textile field and its applications can be gained.

2. Method

The research uses response surface methodology to construct models. However, to produce an in-depth analysis, this study employs three major steps as a research methodology. According to Fig. 1, there are three steps in the research design: (1) data collection, (2) model development, and (3) model evaluation.

Fig. 1Research framework

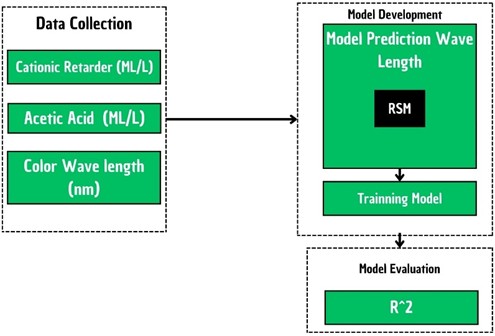
Two variables are dependent on this study and one variable is independent of it. Two dependent variables are the concentration of cationic retardant and the concentration of acetic acid, both of which affect one independent variable, the wavelength, which determines the color aging of the yarn. As shown in Table 1, the optimization model was based on a number of factors.

3. Result and discussion

3.2. Model development

3.2.1. Response surface methodology (linear approach)

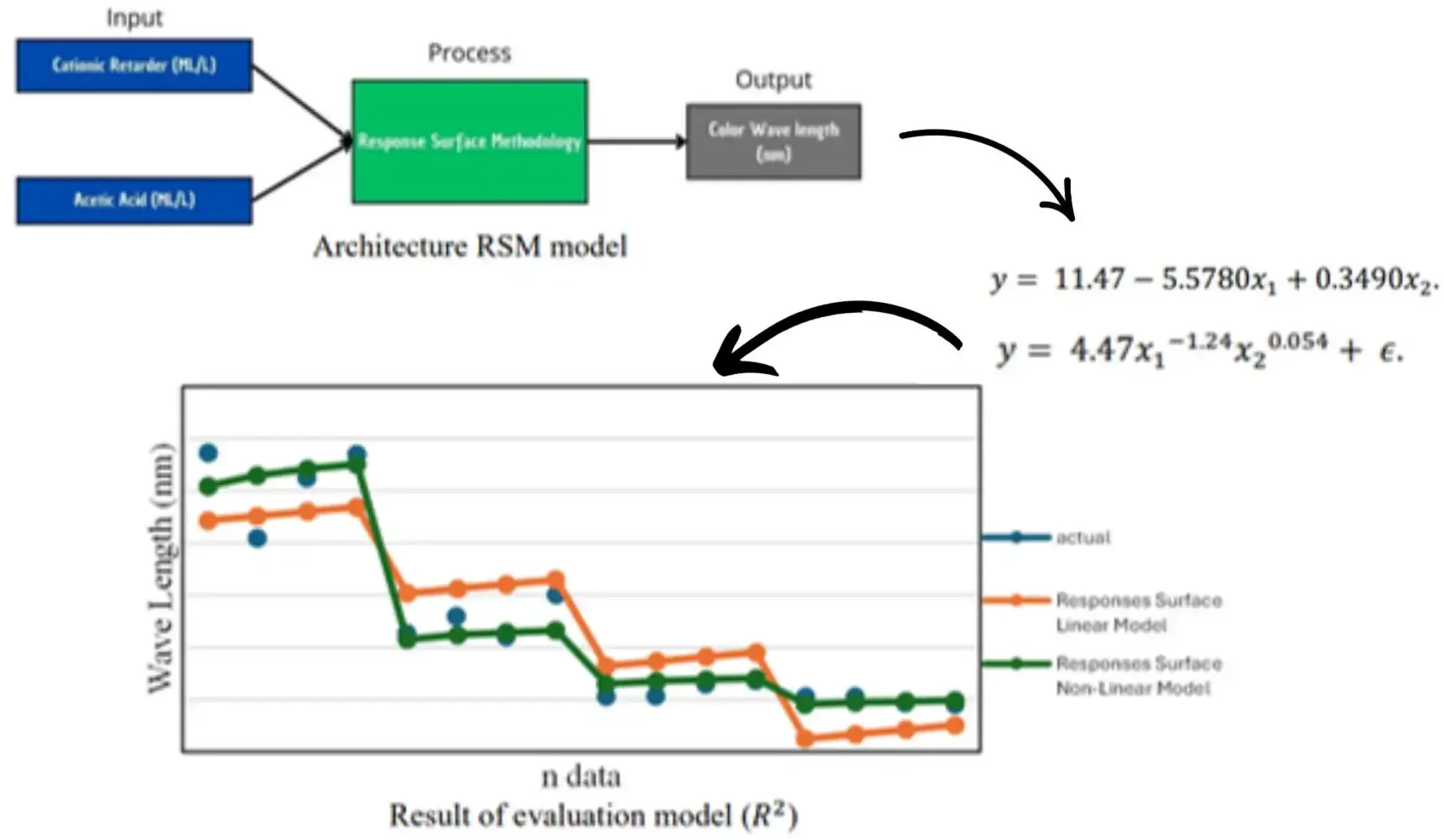
The Response Surface Methodology (RSM) linear model used in this study was developed based on two independent variables: the concentration of cationic retarders ($x_1$) and the concentration of acetic acid ($x_2$), both measured in mL/L. These variables influence color aging, represented by the wavelength ($y$) in nanometers (nm). The RSM linear model is represented by the following equation:

1

$y=a_0+a_1{x}_1+a_2{x}_2+ϵ.$

The independent variables are $x_1$, $x_2$. $A_0$ is the regression model constant, $A_1$ is the regression model constant for $x_1$, $A_2$ is the regression model constant for $x_2$, and $ϵ$ is the regression model error. RSM model architecture is shown in Fig. 2.

Fig. 2Architecture RSM model

To obtain the value of Eq. (1), it can be determined by modeling it as illustrated in Eqs. (2) and (3):

2

${\sum }_{i=1}^n{y}_i=a_0+a_1\sum x_{i1}+a_2\sum x_{i2},$
$y_1=a_0+a_1{x}_{11}+a_2{x}_{12},y_2=a_0+a_1{x}_{21}+a_2{x}_{22},y_n=a_0+a_1{x}_{n1}+a_2{x}_{n2},$

3

$\left(\begin{array}{c}{y}_1\\ :\\ y_n\end{array}\right)=\left(\begin{array}{ccc}1& \dots & x_{1k}\\ 1& ⋰& ⋮\\ 1& \dots & x_{nk}\end{array}\right)\left(\begin{array}{c}{a}_0\\ :\\ a_k\end{array}\right),y_i=x_{ik}{a}_k,y=Xa.$

The difference between the experimental data, ($\widehat{y_i}$) and ($y_i$) model model is defined as the error $\left(ϵ\right)$, which is as follows:

$\sum _{i=1}^n\left(\mathrm{}{\widehat{y}}_i-y_i\right)=ϵ.$

Eqs. (4) and (5) we used to find a for model:

4

$a=(X^{T}X{)}^{-1}{X}^{T}y,$

with:

5

$y=Xa=X(X^{T}X{)}^{-1}{X}^{T}y.$

Eq. (5) can be utilized to solve the linear equation formed by Eq (1), resulting in the formulation presented in Eqs. (6) to (9) as follows

6

$y_i=a_0+a_1{x}_1+a_2{x}_2ϵ,$
$y_1=a_0+a_{1}0.5+a_{2}0.5,y_2=a_0+a_{1}0.5+a_{2}1,y_3=a_0+a_{1}0.5+a_{2}1.5,$
$y_4=a_0+a_{1}0.5+a_{2}2,y_5=a_0+a_{1}1+a_{2}0.5,y_6=a_0+a_{1}1+a_{2}1,$
$y_7=a_0+a_{1}1+a_{2}1.5,y_8=a_0+a_{1}1+a_{2}2,y_9=a_0+a_{1}1.5+a_{2}0.5,$
$y_{10}=a_0+a_{1}1.5+a_{2}1,y_{11}=a_0+a_{1}1.5+a_{2}1.5,y_{12}=a_0+a_{1}1.5+a_{2}2,$
$y_{13}=a_0+a_{1}2+a_{2}0.5,y_{14}=a_0+a_{1}2+a_{2}1,y_{15}=a_0+a_{1}2+a_{2}1.5,$
$y_{16}=a_0+a_{1}2+a_{2}2.$

Eq. (6) can be converted into matrix form as in Eq. (7):

7

$\left(\begin{array}{c}\begin{array}{c}{y}_1\\ y_2\end{array}\\ y_3\\ \begin{array}{c}{y}_4\\ y_5\\ \begin{array}{c}{y}_6\\ y_7\\ \begin{array}{c}{y}_8\\ y_9\\ \begin{array}{c}{y}_{10}\\ y_{11}\\ \begin{array}{c}{y}_{12}\\ \begin{array}{c}{y}_{13}\\ \begin{array}{c}{y}_{14}\\ y_{15}\\ y_{16}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right)=\left(\begin{array}{ccc}1& 0.5& 0.5\\ 1& 0.5& 1\\ \begin{array}{c}1\\ 1\\ \begin{array}{c}1\\ 1\\ \begin{array}{c}1\\ 1\\ \begin{array}{c}1\\ 1\\ \begin{array}{c}1\\ 1\\ \begin{array}{c}1\\ 1\\ \begin{array}{c}1\\ 1\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}& \begin{array}{c}0.5\\ 0.5\\ \begin{array}{c}1\\ 1\\ \begin{array}{c}1\\ 1\\ \begin{array}{c}1.5\\ 1.5\\ \begin{array}{c}1.5\\ 1.5\\ \begin{array}{c}2\\ 2\\ \begin{array}{c}2\\ 2\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}& \begin{array}{c}1.5\\ 2\\ \begin{array}{c}0.5\\ 1\\ \begin{array}{c}1.5\\ 2\\ \begin{array}{c}0.5\\ 1\\ \begin{array}{c}1.5\\ 2\\ \begin{array}{c}0.5\\ 1\\ \begin{array}{c}1.5\\ 2\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right)\left(\begin{array}{c}{a}_0\\ a_1\\ a_2\end{array}\right).$

The values $a_0$, $a_1$, $a_2$ in Eq. (6) are derived using the parameter optimization method described in Eq. (8). The optimization method employs the Least Squares approach to determine the values of ($a$), which involves solving the partial derivative of the error function concerning ($a$) to find the minimum point:

8a

$a=(X^{T}X{)}^{-1}{X}^{T}y,$
$a={\left[\begin{array}{ccc}\begin{array}{c}16\\ 20\\ 20\end{array}& \begin{array}{c}20\\ 30\\ 25\end{array}& \begin{array}{c}20\\ 25\\ 30\end{array}\end{array}\right]}^{-1},$

8b

$\left[\begin{array}{ccc}\begin{array}{c}1\\ 0.5\\ 0.5\end{array}& \begin{array}{c}1\\ 0.5\\ 1\end{array}& \begin{array}{ccc}\begin{array}{c}1\\ 0.5\\ 1.5\end{array}& \begin{array}{c}1\\ 0.5\\ 2\end{array}& \begin{array}{ccc}\begin{array}{c}1\\ 1\\ 0.5\end{array}& \begin{array}{c}1\\ 1\\ 1\end{array}& \begin{array}{ccc}\begin{array}{c}1\\ 1\\ 1.5\end{array}& \begin{array}{c}1\\ 1\\ 2\end{array}& \begin{array}{ccc}\begin{array}{c}1\\ 1.5\\ 0.5\end{array}& \begin{array}{c}1\\ 1.5\\ 1\end{array}& \begin{array}{ccc}\begin{array}{c}1\\ 1.5\\ 1.5\end{array}& \begin{array}{c}1\\ 1.5\\ 2\end{array}& \begin{array}{cc}\begin{array}{c}1\\ 2\\ 0.5\end{array}& \begin{array}{ccc}\begin{array}{c}1\\ 2\\ 1\end{array}& \begin{array}{c}1\\ 2\\ 1.5\end{array}& \begin{array}{c}1\\ 2\\ 2\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right]\left[\begin{array}{c}11.46\\ 8.18\\ \begin{array}{c}10.49\\ 11.39\\ \begin{array}{c}4.52\\ 5.18\\ \begin{array}{c}4.41\\ \begin{array}{c}6.01\\ 2.11\\ \begin{array}{c}2.12\\ 2.59\\ \begin{array}{c}2.72\\ 2.10\\ \begin{array}{c}2.09\\ \begin{array}{c}1.87\\ 1.80\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right]$
$=\left[\begin{array}{ccc}\begin{array}{c}0.6875\\ -0.2500\\ -0.2500\end{array}& \begin{array}{c}-0.2500\\ 0.2000\\ 0\end{array}& \begin{array}{c}-0.2500\\ 0\\ 0.2000\end{array}\end{array}\right],$

8c

$\left[\begin{array}{ccc}\begin{array}{c}1\\ 0.5\\ 0.5\end{array}& \begin{array}{c}1\\ 0.5\\ 1\end{array}& \begin{array}{ccc}\begin{array}{c}1\\ 0.5\\ 1.5\end{array}& \begin{array}{c}1\\ 0.5\\ 2\end{array}& \begin{array}{ccc}\begin{array}{c}1\\ 1\\ 0.5\end{array}& \begin{array}{c}1\\ 1\\ 1\end{array}& \begin{array}{ccc}\begin{array}{c}1\\ 1\\ 1.5\end{array}& \begin{array}{c}1\\ 1\\ 2\end{array}& \begin{array}{ccc}\begin{array}{c}1\\ 1.5\\ 0.5\end{array}& \begin{array}{c}1\\ 1.5\\ 1\end{array}& \begin{array}{ccc}\begin{array}{c}1\\ 1.5\\ 1.5\end{array}& \begin{array}{c}1\\ 1.5\\ 2\end{array}& \begin{array}{cc}\begin{array}{c}1\\ 2\\ 0.5\end{array}& \begin{array}{ccc}\begin{array}{c}1\\ 2\\ 1\end{array}& \begin{array}{c}1\\ 2\\ 1.5\end{array}& \begin{array}{c}1\\ 2\\ 2\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right]\left[\begin{array}{c}11.46\\ 8.18\\ \begin{array}{c}10.49\\ 11.39\\ \begin{array}{c}4.52\\ 5.18\\ \begin{array}{c}4.41\\ \begin{array}{c}6.01\\ 2.11\\ \begin{array}{c}2.12\\ 2.59\\ \begin{array}{c}2.72\\ 2.10\\ \begin{array}{c}2.09\\ \begin{array}{c}1.87\\ 1.80\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right]$
$=\left(\begin{array}{c}{a}_0\\ a_1\\ a_2\end{array}\right)=\left(\begin{array}{c}11.47\\ -5.5780\\ 0.3490\end{array}\right).$

Then, Eq. (9) is derived to assess the wavelength color aging results, as follows:

9

$y=11.47-5.5780x_1+{0.3490x}_2.$

Once the values of $a_0$, $a_1$, dan $a_2$ have been determined, Eq. (9) can be utilized for prediction calculations to demonstrated in Table 3.

Table 3Result RSM linear approach

Wavelength color aging prediction	Wavelength color aging actual
8.8618	11.46
9.0363	8.18
9.2108	10.49
9.3853	11.39
6.0728	4.52
6.2473	5.18
6.4218	4.41
6.5963	6.01
3.2838	2.11
3.4583	2.12

3.2.2. Response surface methodology (non- linear approach)

In this study, the RSM model non linear multiple regression is built around two independent variables: cationic retarder concentration ($x_1$) and acetic acid concentration ($x_2$), both of which influence color aging in terms of wavelength ($y$). The fundamental equation of RSM model multiple regression is given as follows:

10

$y_i=a_0{x_1}^{a_1}{x_2}^{a_2}+ϵ.$

To obtain the value of Eq. (10), it can be determined by modeling it as illustrated in Eqs. (11) and (12):

11

${\sum }_{i=1}^n{y}_i=a_0+a_1\sum x_{i1}+a_2\sum x_{i2},$

$y_1=\mathrm{}{a}_0+a_1\mathrm{}{x}_{11}+a_2\mathrm{}{x}_{12\mathrm{}},\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}{y}_2=\mathrm{}{a}_0+a_1\mathrm{}{x}_{21}+a_2\mathrm{}{x}_{22\mathrm{}},\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}{y}_n=a_0+a_1\mathrm{}{x}_{n1}+a_2\mathrm{}{x}_{n2},$

12

$\left(\begin{array}{c}{y}_1\\ :\\ y_n\end{array}\right)=\left(\begin{array}{ccc}1& \dots & x_{1k}\\ 1& ⋰& ⋮\\ 1& \dots & x_{nk}\end{array}\right)\left(\begin{array}{c}{a}_0\\ :\\ a_k\end{array}\right),y_i=x_{1k}{a}_{k,},y=XA.$

Eqs. (13 and 14) we used to find a for model:

13

$A=(X^{T}X{)}^{-1}{X}^{T}y,$

14

$y=Xa=X(X^{T}X{)}^{-1}{X}^{T}y.$

Eq. (14) can be utilized to solve the nonlinear equation formed by Eq (10), resulting in the formulation presented in Eqs. (15) to (22) as follows:

15

$y=a_0{x_1}^{a_1}{x_2}^{a_2},$

16

$\ln y=\ln (a_0{x_1}^{a_1}{x_2}^{a_2}),$

17

$\ln y=\ln a_0+a_1\ln x_1+a_2\ln x_2,$

18

$Y_i=A_0+A_1{X}_1+A_2{X}_2,$

19

$Y_1=A_0+A_1-0.69+A_2-0.69,Y_2=A_0+A_1-0.69+A_{2}0,$
$Y_3=A_0+A_1-0.69+A_{2}0.40,Y_4=A_0+A_1-0.69+A_{2}0.69,$
$Y_5=A_0+A_{1}0+A_2-0.69,Y_6=A_0+A_{1}0+A_{2}0,$
$Y_7=A_0+A_{1}0+A_{2}0.40,Y_8=A_0+A_{1}0+A_{2}0.69,$
$Y_9=A_0+A_{1}0.40+A_2-0.69,Y_{10}=A_0+A_{1}0.40+A_{2}0,$
$Y_{11}=A_0+A_{1}0.40+A_{2}0.40,Y_{12}=A_0+A_{1}0.40+A_{2}0.69,$
$Y_{13}=A_0+A_{1}0.69+A_2-0.69,Y_{14}=A_0+A_{1}0.69+A_{2}0,$
$Y_{15}=A_0+A_{1}0.69+A_{2}0.40,Y_{16}=A_0+A_{1}0.69+A_{2}0.69.$

The value of $a_0,a_1,a_2$ in Eq. (19) are obtained through the parameter optimization method, as in Eq. (20):

20a

$a=(X^{T}X{)}^{-1}{X}^{T}y,$
$a={\left[\begin{array}{ccc}\begin{array}{c}16\\ 1.8\\ 1.6\end{array}& \begin{array}{c}1.8\\ 4.6\\ 0.2\end{array}& \begin{array}{c}1.6\\ 0.2\\ 4.5\end{array}\end{array}\right]}^{-1},$

20b

$\left[\begin{array}{ccc}\begin{array}{c}1\\ -0.69\\ -0.69\end{array}& \begin{array}{c}1\\ -0.69\\ 0\end{array}& \begin{array}{ccc}\begin{array}{c}1\\ -0.69\\ 0.40\end{array}& \begin{array}{c}1\\ -0.69\\ 0.69\end{array}& \begin{array}{ccc}\begin{array}{c}1\\ 0\\ -0.69\end{array}& \begin{array}{c}1\\ 0\\ 0\end{array}& \begin{array}{ccc}\begin{array}{c}1\\ 0\\ 0.40\end{array}& \begin{array}{c}1\\ 0\\ 0.69\end{array}& \end{array}\end{array}\end{array}\end{array}\right.$
$\left.\begin{array}{ccc}\begin{array}{c}1\\ 0.40\\ -0.69\end{array}& \begin{array}{c}1\\ 0.40\\ 0\end{array}& \begin{array}{ccc}\begin{array}{c}1\\ 0.40\\ 0.40\end{array}& \begin{array}{c}1\\ 0.40\\ 0.69\end{array}& \begin{array}{cc}\begin{array}{c}1\\ 0.69\\ -0.69\end{array}& \begin{array}{ccc}\begin{array}{c}1\\ 0.69\\ 0\end{array}& \begin{array}{c}1\\ 0.69\\ 0.40\end{array}& \begin{array}{c}1\\ 0.69\\ 0.69\end{array}\end{array}\end{array}\end{array}\end{array}\right]\left[\begin{array}{c}2.43\\ 2.10\\ \begin{array}{c}2.35\\ 2.43\\ \begin{array}{c}1.50\\ 1.64\\ \begin{array}{c}1.48\\ \begin{array}{c}1.79\\ 0.74\\ \begin{array}{c}0.75\\ 0.95\\ \begin{array}{c}1.00\\ 0.74\\ \begin{array}{c}0.73\\ \begin{array}{c}0.62\\ 0.58\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right]$
$=\left[\begin{array}{ccc}\begin{array}{c}00678\\ -0.0254\\ -0.0238\end{array}& \begin{array}{c}-0.0254\\ 0.2264\\ -0.0009\end{array}& \begin{array}{c}-0.0238\\ -0.0009\\ 0.2314\end{array}\end{array}\right],$

20c

$\left[\begin{array}{ccc}\begin{array}{c}1\\ -0.69\\ -0.69\end{array}& \begin{array}{c}1\\ -0.69\\ 0\end{array}& \begin{array}{ccc}\begin{array}{c}1\\ -0.69\\ 0.40\end{array}& \begin{array}{c}1\\ -0.69\\ 0.69\end{array}& \begin{array}{ccc}\begin{array}{c}1\\ 0\\ -0.69\end{array}& \begin{array}{c}1\\ 0\\ 0\end{array}& \begin{array}{ccc}\begin{array}{c}1\\ 0\\ 0.40\end{array}& \begin{array}{c}1\\ 0\\ 0.69\end{array}& \end{array}\end{array}\end{array}\end{array}\right.$
$\left.\begin{array}{ccc}\begin{array}{c}1\\ 0.40\\ -0.69\end{array}& \begin{array}{c}1\\ 0.40\\ 0\end{array}& \begin{array}{ccc}\begin{array}{c}1\\ 0.40\\ 0.40\end{array}& \begin{array}{c}1\\ 0.40\\ 0.69\end{array}& \begin{array}{cc}\begin{array}{c}1\\ 0.69\\ -0.69\end{array}& \begin{array}{ccc}\begin{array}{c}1\\ 0.69\\ 0\end{array}& \begin{array}{c}1\\ 0.69\\ 0.40\end{array}& \begin{array}{c}1\\ 0.69\\ 0.69\end{array}\end{array}\end{array}\end{array}\end{array}\right]\left[\begin{array}{c}2.43\\ 2.10\\ \begin{array}{c}2.35\\ 2.43\\ \begin{array}{c}1.50\\ 1.64\\ \begin{array}{c}1.48\\ \begin{array}{c}1.79\\ 0.74\\ \begin{array}{c}0.75\\ 0.95\\ \begin{array}{c}1.00\\ 0.74\\ \begin{array}{c}0.73\\ \begin{array}{c}0.62\\ 0.58\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right]$

In Eq. (20c), $Y$ represents $\mathrm{l}\mathrm{n}\left(y\right)$, $X_1$ represents $\mathrm{l}\mathrm{n}\left(x_1\right)$, and ($X_2$) represents $\mathrm{l}\mathrm{n}\left(x_2\right)$. Therefore, to obtain the value of $a_0$, we utilize the exponential result of ($A_0$) Eq. (21):

21

$\left(\begin{array}{c}{a}_0\\ a_1\\ a_2\end{array}\right)=\left(\begin{array}{c}\mathrm{e}\mathrm{x}\mathrm{p}\left(1.49\right)\\ -1.24\\ 0.054\end{array}\right)=\left(\begin{array}{c}4.47\\ -1.24\\ 0.054\end{array}\right).$

Then, Eq. (21) is derived to assess the wavelength color aging results, as follows:

22

$y=4.47{x_1}^{-1.24}{x_2}^{0.054}+ϵ.$

Once the values of $a_0$, $a_1$, and $a_2$, $a_3$ have been determined, Eq. (22) can be utilized for prediction calculations to assess the quality of fabric cutting, as demonstrated in Table 4.

Table 4Result iteration non-linear model

Wavelength color aging prediction	Wavelength color aging actual
10.59	11.46
10.84	8.18
11.02	10.49
10.18	11.39
4.47	4.52
4.58	5.18
4.65	4.41
4.30	6.01
2.70	2.11
2.76	2.12

3.4. Analyze evaluation result

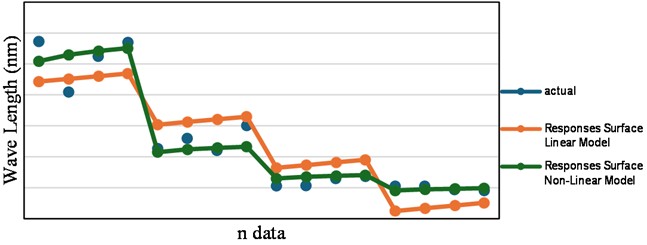
The $R^2$ method evaluated both RSM models for their ability to optimize the dyeing process by utilizing two cationic retardant solutions and acetic acid that affect color Aging. The non-linear RSM model showed superiority in optimizing the dyeing process as it had a higher $R^2$ value of 96 % compared to the linear RSM model of 86 % in explaining variance. The non-linear RSM model is very effective for optimizing the dyeing process, especially when predicting yarn color aging against cationic retardants and acetic acid concentration. The non-linear RSM model can explain 96 % of the variance of the dyeing process. According to Fig. 3, the non-linear RSM model explains 96 % of the data variance with a data distribution similar to the actual data.

The prediction difference of approximately 0.87 nm, although numerically small, is practically significant in the textile dyeing process. For example, when the actual measured wavelength was 11.46 nm, the linear model predicted only 8.8618 nm, resulting in a discrepancy of 2.5982 nm. In contrast, the non-linear model provided a predicted value of 10.59 nm, reducing the prediction error to just 0.87 nm. Even such minor deviations in wavelength can result in perceptible changes in fabric colour intensity or shade, potentially leading to quality control rejections or inconsistencies across production batches. In high-precision industrial applications, such as those involving brand-specific colour standards, maintaining wavelength accuracy within narrow tolerances is essential. This highlights the industrial value of the non-linear RSM model, not only in terms of statistical performance but also in its practical ability to support consistent production quality. Therefore, the improved predictive performance of the non-linear model offers a more reliable foundation for dyeing process optimisation in real-world scenarios.

Fig. 3Result of evaluation model (R2)

4. Conclusions

The objective of this study was to develop and formulate a model to optimize polyacrylate dyeing process parameters with cationic retarders and acetic acid concentrations that affect color wavelength, a measure of yarn color aging. With an $R^2$ value of 0.96, the model built using Response Surface Methodology (RSM) based on non-linear characteristics showed high accuracy. Models based on the linear-based RSM also showed good determination for optimizing polyacrylate yarn dyeing parameters with an $R^2$ value of 0.86. As a result, this value is relatively lower than that of the non-linear RSM model.

Therefore, the evaluation results show that the non-linear RSM-based model is proposed to optimize the concentration of cationic retarders and acetic acid to provide the optimal composition that can influence the wavelength as an indicator of color aging in dyed yarns as desired. The findings of this study have practical implications, especially for professionals in the textile industry, as a model that can optimize the dyeing process parameters, thereby achieving maximum dyeing results.

The prediction difference of approximately 0.87 nm, such as the deviation between the actual wavelength of 11.46 nm and the non-linear model prediction of 10.59 nm, is considered practically significant. In the textile dyeing industry, even such small deviations in wavelength can cause perceptible differences in color intensity or shade, which could lead to inconsistencies across batches or failure to meet brand-specific color standards. Thus, the improved predictive performance of the non-linear model makes it more suitable for real-world applications where precision in color matching is essential.

With the remarkable accuracy of the non-linear RSM model and minimal error rate, this study highlights the effectiveness of statistical approaches such as RSM in analyzing and optimizing manufacturing processes. This research provides suggestions for future research where there is still room for improvement, especially in providing parameter optimization by adding various uncertain variables as factors to be optimized, such as temperature, fixation time, or material types, to improve model robustness and applicability across broader industrial conditions.