Abstract
Urban road traffic flow is affected by many factors, such as road topology, road state and traffic control, among which there are complex spatial correlations and spatiotemporal dynamics, making it difficult to predict the results and accuracy. Therefore, a hybrid forecasting method for short-term traffic flow of urban roads based on integrated neural network is proposed. Collect and preprocess urban road traffic data to build a historical traffic flow dataset. Elman neural network is used to construct periodic sequence prediction sub network, long-term and short-term memory neural network is used to construct continuity prediction sub network, and ELM neural network is used to construct correlation prediction sub network. According to the traffic flow characteristics of the historical traffic flow data set, the related sequence set is constructed and allocated to each sub network. Through the global hybrid forecasting process, using the integration method based on parameter matrix, the outputs of three neural networks are mixed to obtain the final short-term traffic flow hybrid forecasting results of urban roads. Experiments have shown that the proposed algorithm can achieve relatively accurate traffic flow forecasting results, with an absolute percentage deviation of less than 1.6 % and high forecasting accuracy.
1. Introduction
The urban road transportation system is a complex system of road networks, vehicles and traffic participants. It includes urban roads, traffic signal control systems, parking facilities and other infrastructures, as well as vehicles and pedestrians traveling in them and other traffic participants. Urban road traffic flow prediction is an important step in achieving traffic intelligence [1], which plays a very important role in improving road traffic efficiency and alleviating traffic congestion [2]. Short-term traffic flow prediction, i.e., accurate prediction of future short-term traffic flow, is an important basis for effective traffic management and control [3-5]. Accurate prediction of short-term traffic flow on urban roads can provide an important basis for traffic control and optimization. By predicting the future traffic flow, the urban traffic management department can take corresponding traffic control measures according to the prediction results, such as reasonable setting of signal timing, recommended traffic turn and restriction of access, this effectively solves the problem of urban traffic congestion and improves the efficiency of urban transportation. Urban road traffic system has a high degree of complexity, affected by a variety of factors [6-8], such as road conditions, weather, holidays, etc., this poses a great challenge to the prediction of short-term traffic volume. Therefore, applying hybrid models to short-term traffic flow prediction of urban roads is a very meaningful task.
At present, many researchers have conducted research on traffic flow prediction. Mirzahossein et al. [9] combined the deep learning algorithm and machine learning algorithm to build a hybrid model. This method considers both historical traffic data and real-time traffic data, which can better reflect the dynamic changes of traffic flow and improve the prediction accuracy by using traffic flow models. However, the hybrid model built by this method needs to constantly adjust and optimize the model parameters. If the parameters are set improperly, the accuracy of traffic flow prediction will be affected. Patel et al. [10] used the mixed traffic equivalent coefficient to determine the saturated traffic flow of urban road intersections. The mixed traffic equivalent coefficient is used to evaluate the influence of different types of vehicles on the traffic flow, convert different types of vehicles, and unify them into a standard model to calculate the traffic flow. This method considers the traffic characteristics of different types of vehicles and can more accurately reflect the traffic conditions of urban signalized intersections. However, the mixed traffic equivalent coefficient needs to consider the driving characteristics of different vehicles, such as vehicle speed, vehicle weight, vehicle type, etc. If the factors are not fully considered, the accuracy of traffic flow prediction will be affected. Raskar et al. [11] used meta heuristic method to improve hidden Markov model and realize traffic flow prediction. Meta heuristics can find high-quality solutions in a short time, which is very beneficial for processing large-scale traffic data and complex traffic flow forecasting problems. Meta heuristics are used to deal with various complex constraints and objective functions, so that hidden Markov model can better adapt to the complexity and uncertainty of actual traffic flow prediction. However, meta heuristics usually require a long search time, which may become a problem when dealing with large-scale traffic flow data sets, and cannot meet the convergence speed requirements when forecasting traffic flow.
In order to address the shortcomings of the above two methods in traffic flow prediction, this project plans to adopt a new fusion neural network model and apply it to short-term traffic flow prediction of urban roads. Using historical traffic data to train multiple neural network models, on this basis, a comprehensive method based on multi-layer neural networks was proposed for short-term traffic flow prediction of urban roads.
2. A hybrid prediction method for short-term traffic flow on urban roads
2.1. Analysis of short-term traffic flow forecasting problems
The short-term traffic flow forecasting problem is defined as: forecasting the traffic flow of an observation point in the next time interval within a certain time interval [12]. Short-term traffic flow prediction on urban roads generally uses intervals of 5-30 minutes. the traffic flow of the th observation point in the th time gap is recorded as , and at the gap , the urban road traffic flow sequence is . Among them, is all the observation points in the urban road traffic flow prediction area. At this time, the urban road traffic flow prediction task is the predicted gap traffic flow or traffic flow . Let the traffic flow on the city roads during a certain time gap be , and the traffic flow on urban roads has the following characteristics:
(1) Continuity: The traffic flow on urban roads exhibiting proximity characteristics is , of which is a collection of traffic trajectories. That is, the traffic flow of each time gap, often affected by the flow of the previous time gap [13], but also affect the traffic flow of the next time gap. Usually in a day, the most active time periods of urban road traffic flow are morning and evening peaks.
(2) Correlation: urban road traffic flows that exhibit trend characteristics is .
(3) Periodicity: The traffic flow on urban roads showing periodic characteristics is . Periodic urban road traffic flow consists of a sequence of multiple days prior to the predicted time gap that is the same as the predicted time gap [14]. Traffic flow in urban areas is cyclical, i.e., it is approximately the same for each day of the same month with the same time gap.
In order to better take into account the influence of spatial and temporal factors on traffic flow [15], urban area roads were divided into a, based on latitude and longitude of a grid map, where 1 grid represents 1 region. The inbound and outbound traffic flows of the th row and th column grid( are defined as:
Among them, is one of the trajectories in , the is the coordinates of the geographic location, the is the point at which in grid. For each time gap , area to the traffic inflow and outflow is , . According to the inflow and outflow of all grids in the urban road area, the space-temporal matrix is established as follows:
On this basis, a new and fast method for predicting urban road traffic volume is proposed. i.e., the use of integrated neural networks to obtain the corresponding moments of value.
2.2. Integrated neural network construction for short-term traffic flow hybrid prediction on urban roads
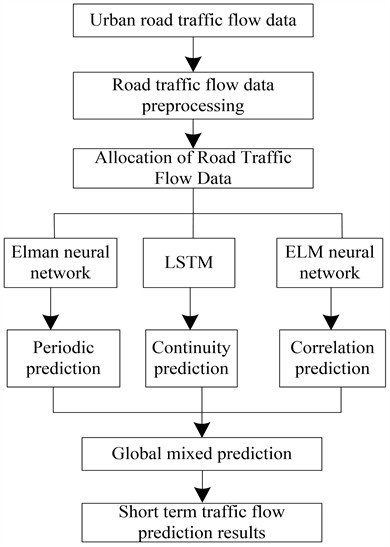
Based on the traffic flow characteristics of urban roads analyzed in the previous subsection, according to the traffic flow data with different characteristics, the neural networks suitable for them are used to predict the traffic flow, using the integration strategy to mix multiple neural networks, and designing the structure of the traffic flow fusion prediction model based on the integrated neural network as shown in Fig. 1.
A neural network-based short-term mixed prediction method for urban road traffic flow is proposed. Each neural network is independent yet cooperates with one another. Collect and preprocess urban road traffic data to obtain historical traffic flow data. When short-term traffic flow hybrid prediction of urban roads is conducted, the collected historical data of urban road traffic flow is preprocessed, and the correlation sequence set is constructed according to the characteristics of historical data of urban road traffic flow. On this basis, correlation analysis and comprehensive evaluation of road network traffic at each intersection in the road network are conducted to determine the network structure and initial parameters of each node. Provide urban road traffic flow training samples for each neural network. The local prediction neural network based on the correlation series of urban road traffic flow includes three types: periodic prediction sub network, continuous prediction sub network and correlation prediction sub network. According to the characteristics of various urban traffic flow sequences, the periodic prediction sub network is realized by Elman neural network, the continuity prediction sub network is realized by long short memory neural network, and the correlation prediction sub network is realized by ELM neural network. The local prediction of the prediction sub network is divided into two parts, one is how to train the network, and the other is how to implement the prediction. The sub neural network can run offline and has learning ability. For the convenience of use and management, each neural network will establish a file. The file is composed of two parts, one part contains the structural characteristics of neural network and the significance of input and output units. The other part is the standard sample of neural network learning. In the learning process of neural networks, automatic recognition of the road network is achieved by calling traffic flow information in the network. The learned results, namely weights and weights, are also saved in the form of files to form a knowledge base integrated with the network. Each sub neural network implements the urban road traffic flow forecast under the condition of sound archives and knowledge. The mixed prediction network is used to receive the traffic flow prediction results of each sub neural network, and the integrated algorithm is used to carry out the mixed prediction of the prediction results of each neural network. The integrated neural network includes three predictive neural networks and one hybrid network. Each output in the prediction sub network corresponds to the input of the hybrid network.
Fig. 1Integrated neural network for mixed prediction of short-term traffic flow on urban roads
2.3. Periodic prediction of traffic flow based on Elman neural network
Elman neural network adds a receiving layer in the hidden layer of the feedforward network as a delay operator to achieve the purpose of memory, therefore, neural networks have strong adaptability to time-varying characteristics [16], which can more intuitively reflect the dynamic characteristics of urban road traffic. An artificial neural network consists of an input layer, a hidden layer, a receiving layer, and an output layer. The input layer unit only plays the role of transmitting urban road traffic flow data, while the output layer performs linear weighting on the input signal. Linear or nonlinear functions [17] can be used to transmit hidden layer elements, and the receiving layer is also called the state layer, which is used to remember the output value of the urban road traffic flow at the previous time of the hidden layer unit and return it to the input as a one-step delay operator. The Elman neural network is characterized by the correlation between the output of the hidden layer and the input of the hidden layer during the receiver layer delay and storage process [18]. This self linking mode makes it sensitive to the data of the historical state of urban road traffic flow. The addition of internal feedback network increases the network’s ability to process the dynamic information of urban road traffic flow [19], thus achieving the purpose of dynamic modeling.
The nonlinear state space expression of short-term traffic flow prediction of urban roads based on Elman neural network is shown in Eqs. (4-6):
Among them, , , , respectively represents dimensional output node vector, dimensional intermediate layer node unit vectors, dimensional time series of multisection traffic flow on a subway network processed by phase-space reconstruction techniques and dimensional feedback state vector. , and respectively describe the transition from the intermediate layer to the output layer, from the input layer to the intermediate layer, and from the takeover layer to the intermediate layer. Among them, is the transfer function of the output neuron, which is formed by the linear composite of the intermediate output signal. Among them, is the transfer function of the middle layer cells, usually using a shape. Elman network uses the sum of error squares as the learning index function, and its expression is as follows:
Among them, is the predicted output value of short-term traffic flow on periodic urban roads.
Using traindx as the training function, i.e. momentum, and adopting an adaptive gradient descent method, the stability of the neural network is improved. The gradient decreasing momentum learning function Learngdm is used as the rule learning. Using input and neuron errors to calculate the rate of weight or threshold change, the learning rate and momentum constant of the weight or threshold; The Tansig function and Purelin function were used to analyze the hidden layer nodes and output layer.
2.4. Traffic flow continuity prediction based on long-term short-term memory neural network
The traffic flow is random, and the relevant parameters such as flow and speed are easily affected by the actual road conditions, traffic control and other factors, presenting non-linear characteristics. Long short-term memory neural networks have high accuracy, wide storage space distribution, strong learning ability, strong noise resistance, and good robustness to noisy neural networks, can fully approximate the complex nonlinear relationship [20], and also has the function of associative memory, this method can effectively solve the short-term traffic volume prediction problem of continuous urban road sections. Long short-term memory neural networks (LSTM) are a type of recursive neural network that shares the same characteristics as other neural networks (input layer, loop hidden layer, output layer). The difference between them is the hidden layer, and LSTM consists of a hidden layer composed of storage units. The memory unit is a powerful structure, which determines and stores the short-term traffic flow status of urban roads through the memory unit, mainly including input gate, forgetting gate and output gate. On this basis, using input gate circuits to achieve new input of short-term traffic flow data on urban roads and controlling it; Forgetting gate determines the amount of cell state information discarded at the last moment; The output gate controls which information of the current unit state is exported. Set the short-term traffic flow sequence of urban road input LSTM as , the hidden layer state as . At the time , the calculation process of using LSTM to predict the traffic flow of continuous urban roads is as follows:
where, the , , represent input gates, forget gates, and output gates, respectively; the , respectively represent the output of the memory cells as well as the hidden layer at the moment ; the , and are the weights of the input gate, implicit layer, and memory cell, respectively; the , and the weights of the forgetting gate, the implicit layer, and the memory cell, respectively; the and denote the weight matrices of the memory cells as well as the implicit layer, respectively; the , and are the weights of the output gate, the implicit layer, and the memory cell, respectively; the , , and represent the bias of each function, respectively; the and are all activation functions, thedenotes the vector inner product.
The training process of the LSTM model for predicting urban road traffic flow is as follows: Randomize the weight matrix and the offset. In this model, an input vector is introduced to the input layer. Then, calculate the values of the forgetting gate, output gate of the first hidden layer, as well as the input vector and state value of the memory unit. Obtain the output vector of the memory module and take it as the input vector of the next hidden layer. Repeat this process to get the prediction value of continuous urban road traffic flow. According to the predicted value of urban road traffic flow, the error function is calculated, and the weight value of the error back-propagation is updated. The training ends when the maximum iteration number is reached. The trained model is used to predict the final continuous urban road traffic flow prediction results.
2.5. Traffic flow correlation prediction based on ELM neural network
Short term traffic flow is highly time-varying, nonlinear and uncertain. However, for a specific observation point, the longer the observation time is, the more certain and regular the traffic flow statistical behavior will be. Due to the short observation time, short-term traffic flow is greatly affected by random factors. The statistical behavior is often unsteady, aperiodic or quasi periodic, or even random, which makes prediction difficult. The grey model is used to accumulate the short-term traffic flow data, change the short-term traffic flow into the long-term traffic flow, use the characteristics of the long-term traffic flow with obvious regularity and strong certainty to predict the long-term traffic flow, and then restore it to the short-term traffic flow prediction results, so as to improve the prediction accuracy. Grey theory uses limited data to evaluate uncertain behavior, builds first-order differential equation by accumulating original data, and uses exponential curve to fit data to reveal the change trend of traffic flow and predict traffic flow. However, the data series fitted by grey theory is exponential smooth curve, and the prediction will often be distorted when the fluctuation of traffic flow is large. ELM neural network is a feedforward neural network with a single hidden layer. By randomly selecting the weights and thresholds of the hidden layer of the network, the parameter training problem is transformed into the problem of solving incompatible linear equations. Compared with the traditional BP network, it has the characteristics of simple training and fast training speed. In order to solve the distortion phenomenon when the grey model fits the fluctuating data, the original correlation urban road traffic flow data is grey processed, input into the ELM neural network training, and get the relationship between input and output. This paper proposes a method based on least squares support vector, which can effectively solve the problem of linear whitening differential equations.
Let the collected correlated urban road traffic flow dataset be , , dividing it into groups, each data group and satisfy , , . The first of the th group of urban road traffic flow data is . Data in is processed in grey, to obtain one time accumulated sequence of . Among them, . Select the first term of as the input of ELM neural network, and the first item as the expected output of ELM neural network with:
The input matrix set and the target output matrix set of the ELM neural network are formed by the above urban road traffic flow data divided into groups, thus, the true output matrix of the network was obtained. is the connection weight between the input layer and the hidden layer, the is the number of neurons in the hidden layer, the is the threshold of a hidden layer of node , the is the weights of the hidden and output layers, among them, represents the connection weight between the hidden layer node and the output layer. Set sigmoid function as the hidden excitation function, and its expression is as follows:
When urban road traffic flow inputs is , according to the principle of neural network, the expression of the hidden layer for the inputs of the nodes is as follows:
The output of the th node of the hidden layer is expressed as follows:
The expression of the urban road traffic flow correlation prediction result output by the network output layer is as follows:
Perform short-term correlation prediction on urban roads through the above ELM neural network operations.
2.6. Integration of neural networks for global hybrid prediction of short-duration traffic flow on urban roads
The outputs of the three neural networks are blended through a global hybrid prediction process using an integrated method based on a parameter matrix. The influence weights of each neural network are different in the hybrid prediction output. The influence weights of different sub-networks need to be taken into account when mixing the outputs of three neural networks for short-term traffic flow prediction on urban roads. Finally, the integrated neural network was used to predict short-term traffic flow on urban roads and simulated:
Among them, is Hadamarco. , and is the weighting parameter, which reflects the degree of influence of the three sub-neural networks on the short-term traffic flow prediction results of urban roads.
The total loss value of a comprehensive neural network is the average of the predicted value and the true value, and based on this, it is backpropagation to minimize it. The loss function of this integrated neural network is represented as follows:
Among them, is the value of the real traffic flow, the is the value of predicted traffic flow, the is the learning parameter.
Using the above process, the integration method of parameter matrix is used to mix the short-term traffic flow prediction results of the three neural networks and output the final short-term traffic flow prediction results of urban roads.
3. Experimental analysis
This project intends to focus on the main roads as the research object, conduct theoretical analysis on them, and conduct empirical analysis on them. Collect the traffic data of each road section, and process the historical monitoring data provided by the official to obtain experimental samples. The urban road traffic data includes the traffic flow, speed and time occupancy of the monitoring points every other minute. According to the needs of the integrated neural network, select more complete data. Collect the traffic flow of 5 minutes per day for 30 consecutive days. The data set is from June 1 to June 30, 2020. In this study, detailed parameter tuning was conducted for three neural network architectures: Elman, LSTM, and ELM. The Elman network uses 10 hidden neurons with a learning rate set to 0.01, and employs the SGD optimization algorithm with a driving force. It iterates 2000 times to ensure convergence, balancing training speed and accuracy. The LSTM network, due to its advantage in processing long sequences, uses 15 memory units with a learning rate of 0.005 and employs the Adam optimization algorithm. Due to its adaptive learning rate characteristics, it achieves stable prediction through 1500 iterations. The ELM network randomly generates 50 hidden layer nodes and uses the least squares method to quickly solve the output weights without iteration, greatly improving training efficiency. In terms of integration methods, we create a parameter matrix and dynamically allocate weights based on the F1 scores of each sub network on the validation set, such as assigning weights of 0.3, 0.4, and 0.3 to Elman, LSTM, and ELM, respectively, to ensure complementary advantages. These parameter selections are based on cross validation and grid search, aiming to maximize prediction accuracy while controlling overfitting, and ultimately the integrated model significantly improves overall prediction performance. The site map of short-term traffic flow prediction of urban roads is shown in Fig. 2.
Fig. 2Site diagram of short-term traffic flow test on urban roads

The dataset setup for short-term traffic flow prediction on urban roads is shown in Table 1.
The changes in traffic flow on the studied urban roads on June 1, 2020 are shown in Fig. 3.
Table 1Setting of short-term traffic flow prediction dataset for urban roads
Parameter name | Result |
time interval | 30 minutes |
Grid size | 30 m× 30 m |
Number of vehicles counted | Over 50000 |
Number of time intervals | 25486 |
Fig. 3Changes in traffic flow on the research road on June 1st
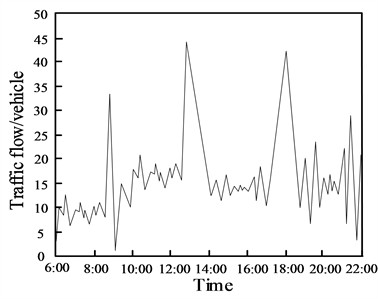
Fig. 3 shows the traffic flow into the urban road area during the day. According to the results of the traffic flow changes in Fig. 3, it can be seen that the urban road area in the 9:00, 13:00, 18:00 time period of the traffic flow is more, indicating that this time is a more concentrated time period of vehicles in the city road.
The changes in traffic flow on the studied urban roads from June 1, 2020 - June 7, 2020 are shown in Fig. 4.
Fig. 4Periodic traffic flow on urban roads
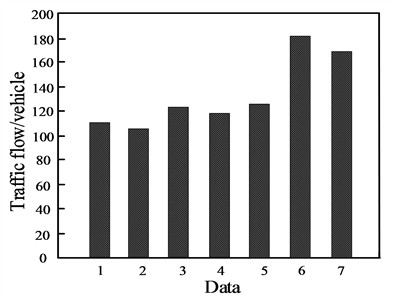
Fig. 4 shows the trend of vehicles entering the roadway during the period of June 1, 2020-June 7, 2020, from 12:30 to 13:00 daily, which corresponds to Monday to Sunday. According to the experimental results of Fig. 4, it can be seen that the number of vehicles entering the area of the roadway is extremely similar on weekdays, while the number of vehicles entering the roadway area on holidays is significantly higher than on weekdays. Fig. 4 of the urban road traffic flow shows the characteristics of cyclic, the integrated neural network used in this paper’s method, taking into account the cyclic characteristics of the urban road traffic flow, verifying that the use of this paper’s method using the integrated neural network has a high degree of reliability.
The number of neurons has a great impact on the prediction performance of the integrated neural network in predicting urban road traffic flow. The number of neurons has a great influence on the generalization ability of neural networks. When there are too many neurons, they tend to remember all training data, including data containing noise, which reduces the generalization ability of neural networks. When the number of neurons is too small, it is impossible to fit all urban road traffic flow sample data, which affects the generalization ability of the neural network. Therefore, it is very important to select the appropriate number of neurons. When counting the number of different neurons, the integrated neural network outputs the root mean squared error (RMSE) of urban road traffic flow prediction results. The statistical results are shown in Fig. 5.
Fig. 5The impact of the number of neurons on network output
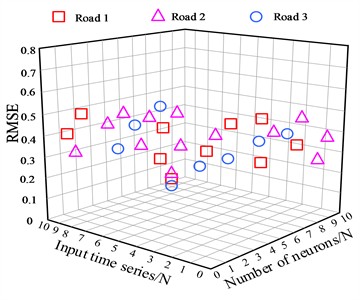
According to the experimental results in Fig. 5, when the number of time series of urban road traffic flow input is 8 and the number of neurons is 7, the integrated neural network has the optimal short-term traffic flow prediction performance of urban roads. At this time, the RMSE value of urban road traffic flow prediction results is lower than 0.1, finally, the optimized short-term road network traffic flow prediction results are presented.
Using the method of this paper, the short-time traffic flow of this urban road on June 16, 2020 is predicted by using integrated neural network, and the prediction results are shown in Fig. 6.
Fig. 6Short term traffic flow prediction results for urban roads
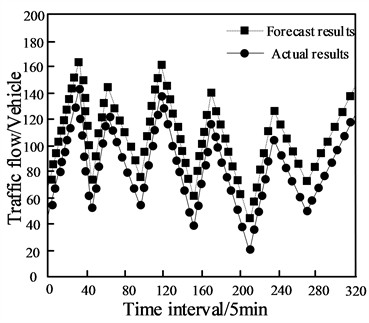
According to the experimental results in Fig. 6, it can be seen that the method in this paper utilizes the integrated neural network to effectively predict the short-time traffic flow of the urban road, and the prediction results of the urban road traffic flow are very close to the actual results. This method combines multiple neural networks to achieve good prediction results for short-term traffic flow on urban roads.
Using the method of this paper using integrated neural network hybrid prediction of urban road traffic flow, hourly traffic flow and daily traffic flow prediction results are shown in Fig. 7.
Fig. 7Short term prediction results of urban road traffic flow
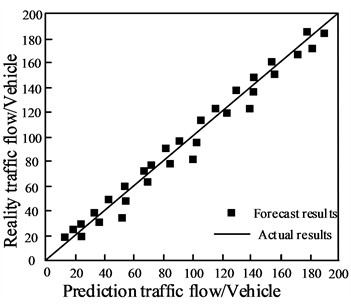
a) Hourly traffic flow prediction results
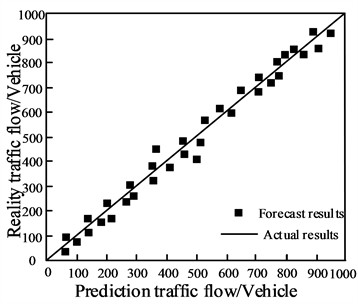
b) Daily traffic flow prediction results
According to the experimental results in Fig. 7, it can be seen that the method of this paper is used to predict the short-term urban road traffic flow, hourly traffic flow and daily traffic flow prediction results, and the actual urban road traffic flow of the difference is very small. The experimental results verify that the method of this paper has high performance in predicting short-term traffic flow on urban roads. The method in this paper utilizes the integrated neural network, combines multiple neural networks, trains multiple neural networks and synthesizes their prediction results to improve the prediction accuracy of short-term traffic flow on urban roads. The hybrid traffic flow prediction results of the integrated neural network improve the overfitting phenomenon of the single neural network, improve the generalization ability of the model, make it more robust to noise and outliers, and have higher prediction accuracy.
Mean Absolute Error (MAE) is the time series length of the estimated traffic volume divided by the absolute difference between the actual traffic volume and the expected traffic volume. This indicator takes the error between the actual traffic flow and the predicted traffic flow as the absolute value, avoiding the positive and negative cancellation when calculating the total error, and better reflects the accuracy of the prediction results. Mean Absolute Percentage Error (MAPE) is the absolute value of the ratio between the difference between the actual traffic flow and the predicted traffic flow and the actual traffic flow, divided by the length of the traffic flow time series to be evaluated. This indicator calculates the relative error between the predicted traffic flow and the actual traffic flow, indicating the average deviation degree between the predicted traffic flow and the actual traffic flow. The method in this paper is used to predict the short-term traffic flow of urban roads, and the absolute deviation and absolute percentage error of the statistical prediction results are shown in Fig. 8.
Analyzing the experimental results in Fig. 8, the absolute deviation and the absolute percentage error of short-time traffic flow prediction using the method of this paper are lower than 10 vehicles per 5 minutes and 1.6 %, respectively. The absolute deviation and absolute percentage error of short-term traffic flow prediction are two important indicators to evaluate the accuracy of the prediction model. The low absolute deviation and absolute percentage error indicate that the model has high accuracy in short-time traffic flow prediction, and the experimental results in Fig. 8 verify that the method in this paper has high accuracy in short-time traffic flow prediction.
The maximum absolute error, average error and average relative error percentage of short-term traffic flow prediction of urban roads are selected as evaluation indicators. The prediction performance of Elman neural network, long-term short-term memory neural network and ELM neural network, and integrated neural network when statistical prediction of short-term traffic flow of urban roads is adopted. The prediction performance evaluation results of each neural network are shown in Table 2.
Fig. 8Absolute deviation and absolute percentage error of short-term traffic flow prediction
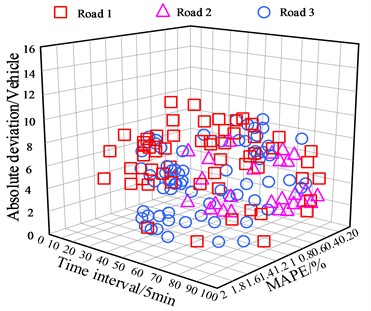
Table 2Comparison of predictive performance of neural networks
Neural network | Maximum absolute error/vehicle | Average error/vehicle | Average relative error percentage |
Elman neural network | 28.5 | 10.5 | 5.4 % |
Long term short-term memory neural network | 19.5 | 9.5 | 6.8 % |
ELM neural network | 17.5 | 7.5 | 4.9 % |
Integrated neural network | 5.8 | 3.5 | 1.4 % |
According to the experimental results in Table 2, it can be seen that compared with the independent neural network, the maximum absolute error, average error and average relative error percentage of the integrated neural network in predicting the short-term traffic flow of urban roads are significantly lower than those of other neural networks. The experimental results verify that the prediction accuracy of the integrated neural network is significantly better than other neural networks. The integrated neural network used in this paper is an effective hybrid prediction method for short-term traffic flow on urban roads with reduced maximum error, average absolute error and average relative error.
The F1 score comparison test results of different neural networks under different road types (main roads, secondary roads, expressways) are shown in Table 3.
Table 3F1 test results of different test models under different road types
Road type | F1 score | |||
Elman neural network | Long term short-term memory neural network | ELM neural network | Integrated neural network | |
Main road | 0.83 | 0.90 | 0.86 | 0.92 |
Secondary trunk road | 0.75 | 0.82 | 0.84 | 0.85 |
Expressway | 0.85 | 0.79 | 0.90 | 0.93 |
From the test results in Table 3, it can be seen that there are significant differences in performance between Elman neural network and ensemble neural network under different road types, and ensemble neural network has outstanding overall advantages. On the main road, the Elman neural network has an F1 score of 0.83, and the ensemble neural network reaches 0.92. The ensemble model performs better, indicating its ability to integrate multiple characteristics and accurately capture traffic flow patterns on the main road. The traffic flow on the secondary road fluctuates greatly, with an Elman neural network F1 score of only 0.75 and an integrated neural network score of 0.85. Although the improvement is not as significant as that on the main road, it still shows stronger adaptability and effectively reduces errors through mixed prediction. On the expressway, the Elman neural network has an F1 score of 0.85 and the ensemble neural network has a score of 0.93, further amplifying the advantages of the ensemble model. Overall, integrated neural networks, with the advantage of integrating multiple neural networks, can better cope with complex traffic flow changes and provide more accurate prediction results under different road types. Compared with a single Elman neural network, it has higher practicality and reliability.
4. Conclusions
A hybrid prediction method of short-term traffic flow on urban roads with integrated neural networks is studied, in which multiple neural network models are constructed, and the integrated learning strategy is used to combine the neural networks to improve the prediction accuracy of the short-term traffic flow data on urban roads, which are highly nonlinear, time-varying and uncertain. Through experimental verification, the method can fully explore and utilize the information in historical traffic data, and use the integrated learning strategy to optimize the combination of models and improve the generalization ability of the models. This method provides new ideas and methods for urban traffic management and control, which can help improve road traffic efficiency, ease traffic congestion, and promote the intelligent and sustainable development of urban transportation. in the future, we can further explore how to optimize the neural network structure and integration strategy to improve the prediction performance and applicability.
References
-
E. Byk, D. A. Lazar, R. Pedarsani, and D. Sadigh, “Incentivizing efficient equilibria in traffic networks with mixed autonomy,” IEEE Transactions on Control of Network Systems, Vol. 8, No. 4, pp. 1717–1729, Dec. 2021, https://doi.org/10.1109/tcns.2021.3084045
-
G. Comert, N. Begashaw, and N. Huynh, “Improved grey system models for predicting traffic parameters,” Expert Systems with Applications, Vol. 177, p. 114972, Sep. 2021, https://doi.org/10.1016/j.eswa.2021.114972
-
T. S. Gomides, R. E. de Grande, R. I. Meneguette, F. S. H. Souza, and D. L. Guidoni, “Predictive congestion control based on collaborative information sharing for vehicular Ad hoc networks,” Computer Networks, Vol. 211, p. 108955, Jul. 2022, https://doi.org/10.1016/j.comnet.2022.108955
-
S. Mondal and A. Gupta, “Non-linear evaluation model to analyze saturation flow under weak-lane-disciplined mixed traffic stream,” Transportation Research Record: Journal of the Transportation Research Board, Vol. 2675, No. 8, pp. 422–431, Mar. 2021, https://doi.org/10.1177/0361198121998370
-
H. K. Saini and S. Biswas, “Estimating lateral placement and lane indiscipline of urban mixed traffic of a developing country: an ANN-assisted approach,” Canadian Journal of Civil Engineering, Vol. 48, No. 11, pp. 1571–1581, Nov. 2021, https://doi.org/10.1139/cjce-2020-0250
-
J. Jiang and J. X. Zhang, “Improved ACO-optimized BP neural network for short-term traffic flow prediction,” Computer Simulation, Vol. 38, No. 7, pp. 97–101, Jul. 2021.
-
F. M. Awan, R. Minerva, and N. Crespi, “Using noise pollution data for traffic prediction in smart cities: experiments based on LSTM recurrent neural networks,” IEEE Sensors Journal, Vol. 21, No. 18, pp. 20722–20729, Sep. 2021, https://doi.org/10.1109/jsen.2021.3100324
-
A. Ghosh and T. Parisini, “Traffic control in a mixed autonomy scenario at urban intersections: an optimal control approach,” IEEE Transactions on Intelligent Transportation Systems, Vol. 23, No. 10, pp. 17325–17341, Oct. 2022, https://doi.org/10.1109/tits.2022.3166452
-
H. Mirzahossein, I. Gholampour, S. R. Sajadi, and A. H. Zamani, “A hybrid deep and machine learning model for short‐term traffic volume forecasting of adjacent intersections,” IET Intelligent Transport Systems, Vol. 16, No. 11, pp. 1648–1663, Jun. 2022, https://doi.org/10.1049/itr2.12224
-
P. N. Patel and A. Dhamaniya, “Developing mixed traffic equivalency factors to estimate saturation flow at urban signalized intersections,” Transportation Research Record: Journal of the Transportation Research Board, Vol. 2675, No. 11, pp. 601–611, Jul. 2021, https://doi.org/10.1177/03611981211018694
-
C. Raskar and S. Nema, “Metaheuristic enabled modified hidden Markov model for traffic flow prediction,” Computer Networks, Vol. 206, p. 108780, Apr. 2022, https://doi.org/10.1016/j.comnet.2022.108780
-
D. Li and J. Lasenby, “Spatiotemporal attention-based graph convolution network for segment-level traffic prediction,” IEEE Transactions on Intelligent Transportation Systems, Vol. 23, No. 7, pp. 8337–8345, Jul. 2022, https://doi.org/10.1109/tits.2021.3078187
-
B. Brik and A. Ksentini, “Toward optimal MEC resource dimensioning for a vehicle collision avoidance system: a deep learning approach,” IEEE Network, Vol. 35, No. 3, pp. 74–80, May 2021, https://doi.org/10.1109/mnet.011.2000577
-
S. Upadhye, S. Neelakandan, K. Thangaraj, D. V. Babu, N. Arulkumar, and K. Qureshi, “Modeling of real time traffic flow monitoring system using deep learning and unmanned aerial vehicles,” Journal of Mobile Multimedia, Vol. 19, No. 2, pp. 477–496, Nov. 2022, https://doi.org/10.13052/jmm1550-4646.1926
-
G. Grande, M. Lesniak, L.-P. Tardif, and J. D. Regehr, “Exploring vehicle probe data as a resource to enhance network-wide traffic volume estimates,” Canadian Journal of Civil Engineering, Vol. 49, No. 4, pp. 558–568, Apr. 2022, https://doi.org/10.1139/cjce-2020-0656
-
G. Zheng, W. K. Chai, V. Katos, and M. Walton, “A joint temporal-spatial ensemble model for short-term traffic prediction,” Neurocomputing, Vol. 457, pp. 26–39, Oct. 2021, https://doi.org/10.1016/j.neucom.2021.06.028
-
A. Kumar and P. S. V. S. Sai Prasad, “Incremental fuzzy rough sets based feature subset selection using fuzzy min-max neural network preprocessing,” International Journal of Approximate Reasoning, Vol. 139, pp. 69–87, Dec. 2021, https://doi.org/10.1016/j.ijar.2021.09.006
-
C. Cummings and H. Mahmassani, “Emergence of 4-D system fundamental diagram in urban air mobility traffic flow,” Transportation Research Record: Journal of the Transportation Research Board, Vol. 2675, No. 11, pp. 841–850, Jul. 2021, https://doi.org/10.1177/03611981211020005
-
N. Singh, K. Kumar, P. Goswami, and H. Jafari, “Analytical method to solve the local fractional vehicular traffic flow model,” Mathematical Methods in the Applied Sciences, Vol. 45, No. 7, pp. 3983–4001, May 2022, https://doi.org/10.1002/mma.8027
-
E. Sofronova and A. Diveev, “Hybrid recurrent traffic flow model with artificial neural networks for approximation of unknown urban road subnetworks,” Procedia Computer Science, Vol. 186, pp. 426–430, Jan. 2021, https://doi.org/10.1016/j.procs.2021.04.163
About this article
This article is supported by the Science and Technology Research Program of Chongqing Municipal Education Commission (Grant No. KJZD-M202502001).
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Xi Zhang: formal analysis, writing-original draft preparation. Jian Yin: conceptualization, methodology, writing-review and editing. Baiying Yang: supervision, formal analysis, validation.
The authors declare that they have no conflict of interest.
