Abstract
This study examines a planar dynamic model of a rotor-bearing-housing system incorporating a polyurethane support insert. The formulation takes into account the inertial, stiffness, and damping properties of the shaft, raceways, rolling elements, and cage, while the polyurethane layer is treated as an additional elastic–dissipative element. The equations of motion are derived using the Lagrangian formalism, based on kinetic, potential, and dissipation energies. Within the article, a frequency response analysis for different coating thicknesses is carried out, showing that the polyurethane insert reduces resonance frequencies by approximately 50-64 % while increasing vibration amplitudes by 67-146 %. A 2 mm layer provides a compromise between stiffness and damping, whereas thicker coatings (3-4 mm) enhance high-frequency vibration isolation but lead to higher sensitivity to low-frequency excitations. The novelty of this study lies in the introduction of a polyurethane elastic-dissipative layer into the planar dynamic model of the rotor-bearing-housing system. This approach enables an analytical representation of the polymer’s stiffness and damping effects and establishes a direct relationship between the polyurethane thickness and the system’s resonance behavior a topic not explicitly treated in previous works.
Highlights
- This study introduces a polyurethane elastic-dissipative layer into the rotor-bearing-housing model, enabling analytical evaluation of its stiffness, damping, and thickness effects on resonance—an aspect not addressed in prior research.
- Thicker polyurethane layers increase damping and amplify vibration response near resonance, which must be considered in design.
- Polyurethane inserts significantly reduce support stiffness, shifting rotor-bearing resonance frequencies downward by 50–64%.
- A 2 mm polyurethane layer provides the most balanced performance, limiting amplitude growth while moderately lowering resonance.
- The developed planar dynamic model enables explicit evaluation of stiffness and damping effects of polyurethane layers on rotor systems.
1. Introduction
The development of accurate and flexible dynamic models of bearing assemblies continues to be one of the key tasks in rotor system engineering. This is mainly because the predictive quality of vibration analysis depends on how well the real stiffness, damping, and compliance of supports are represented. In modern studies, the notion of a planar dynamic model is often applied to describe simplified two-dimensional schemes that nevertheless retain the essential inertial, elastic, and dissipative properties of the bearing components.
Different research groups have proposed alternative modeling strategies. For instance, several authors focused on cylindrical roller bearings, where the raceways, rolling elements, and cage are treated as separate interacting subsystems, which allows for more precise estimation of vibration levels under varying operating regimes [1]. Other works approached the problem within the multibody dynamics framework, where radial-loaded bearings are modeled by discrete connections of masses, springs, and dampers, making it possible to capture both contact stiffness and load transfer across the rolling elements [2]. These examples underline that a proper account of the internal bearing structure substantially improves the accuracy of rotor dynamic predictions.
Recent international studies have also investigated the application of elastomeric and polymeric materials in bearing supports. For example, [3] analyzed vibration attenuation in rotor systems using viscoelastic foundation layers, while [4] proposed a hybrid elastomer-metal support design for improved damping performance. These works confirm the growing relevance of polymer-based damping materials in rotor dynamics and support the direction of the present study.
Domestic investigations provide a complementary perspective. For example, models with elastic foundations have demonstrated that the compliance of the housing plays a decisive role in shaping oscillatory behavior [3]. In addition, discrete parameter descriptions of mass and stiffness distributions in bearing parts have been shown to provide practical simplifications without a significant loss of accuracy [5].
Alongside these analytical approaches, rapid progress in computational techniques has expanded the scope of research. Finite element analysis and advanced simulations now enable detailed evaluation of shaft deflection, stress fields, and vibration responses under realistic operating conditions [6-8]. These works indicate that modifications such as elastomeric layers or hybrid supports can effectively reduce shaft bending and suppress critical vibrations. Still, their efficiency strongly depends on the specific type of machine and load regime. A particularly relevant case is textile machinery, where slender and heavily loaded shafts make damping inserts a promising but not yet sufficiently explored option.
Finally, reviews of rotor systems with hydrodynamic bearings also highlight that accurate modeling is only possible if the damping and compliance of the supports are correctly introduced [9]. Therefore, the integration of modern materials – such as polyurethane layers – into planar models provides a valuable direction for improving predictive capabilities and extending the operational life of rotor-bearing systems.
2. Methods
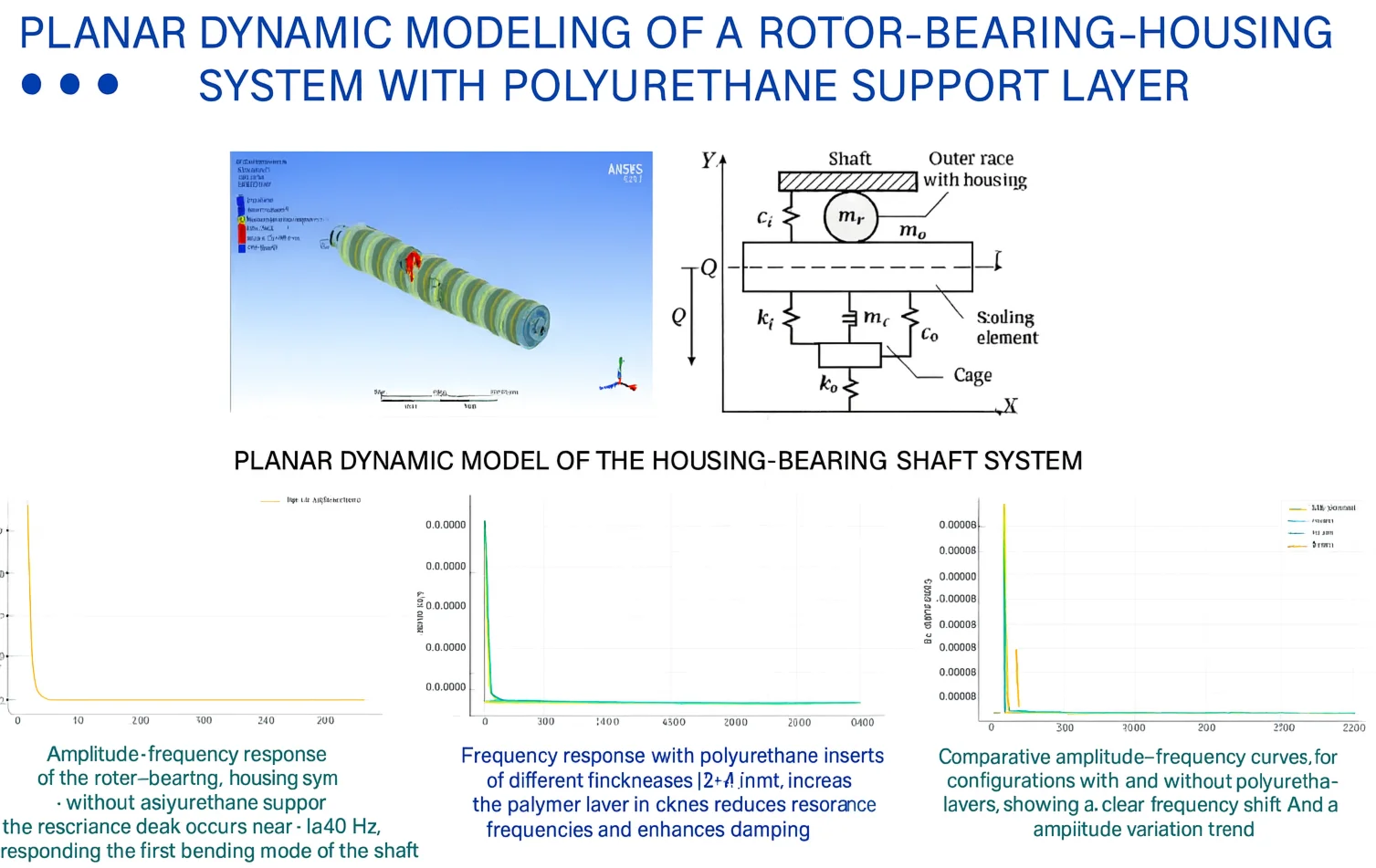
In Fig. 1, a planar dynamic model of the housing-bearing-shaft system is presented. The shaft is shown in the center and is subjected to an external static load applied along the -axis.
The inner raceway is represented by the mass . The rolling elements, with mass , provide load transfer between the inner and outer raceways. The outer raceway together with the housing is modeled by the mass . The cage is represented by the mass and is connected to the system through elastic elements.
The elastic properties of the structure are taken into account through stiffness coefficients , and damping coefficients , . These elements describe the polyurethane coating of the bearing, which introduces additional compliance and energy dissipation.
Thus, the model makes it possible to account for the distribution of masses and the influence of the polyurethane layer on the dynamic behavior of the bearing-support assembly.
Fig. 1A planar dynamic model of the housing-bearing-shaft system
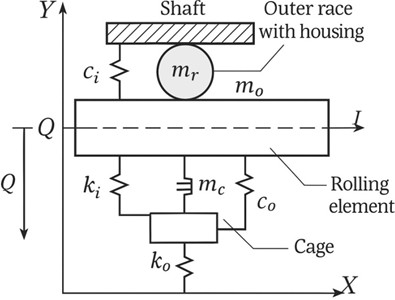
Planar model and generalized coordinates
We consider the translational displacements in the inner ring (shaft) and the outer ring (housing):
where – mass of the shaft with the inner raceway; – mass of the outer raceway with the housing; Equivalent radial connection “inner ↔ outer” (bearing with rolling elements and cage): matrices , ; Connection “outer ring ↔ foundation” (polyurethane coating/bushing): , ; External force acts along (-axis).
The masses and are taken into account parametrically in , (through the contact stiffness of the raceways and the inertial/whirl contribution of the cage). If necessary, they can be decomposed into additional degrees of freedom.
Kinetic energy:
Potential energy (bearing + polyurethane):
wherе , .
Rayleigh dissipation function:
On the basis of the derived expressions for Eq. (2) the kinetic energy , Eq. (3) the potential energy , and Eq. (4) the Rayleigh dissipation function , the equations of motion of the system are obtained from the classical Lagrangian formalism. For each generalized coordinate , the governing equation is written as:
here: , – equivalent radial stiffness/dampers of the bearing (taking into account , ). , – elastic-damping properties of the polyurethane insert/coating in the direction , .
Relation of parameters to the physics of the assembly Bearing (equivalent): is formed from the Hertzian contact stiffness of the raceways and the number of rolling elements with angular distribution : , by identification (vibration response damping).
The influence of , is reflected in the frequency-dependent and in the slight anisotropy (stiffness field ellipse).
Polyurethane: for a thin layer of thickness and support area :
through the loss factor wherе – characteristic natural frequency of the outer “ring-foundation”.
The equations of motion were solved in the MATLAB environment using the state-space formulation. The system matrices of mass (M), damping (C), and stiffness (K) were assembled based on identified parameters of the bearing and polyurethane layer. The numerical integration was performed in the frequency domain using the harmonic balance method, while the amplitude-frequency response was obtained by sweeping the excitation frequency from 0 to 200 Hz.
Table 1Physical and mechanical parameters applied in the planar dynamic model
Parameter | Symbol | Value | Unit | Description |
Shaft mass | 140 | kg | Inner ring + shaft | |
Outer ring + housing mass | 115 | kg | With outer raceway | |
Polyurethane thickness | 2 / 3 / 4 | mm | Variable parameter | |
Elastic modulus | 60 | MPa | Polyurethane | |
Poisson’s ratio | 0.49 | – | Nearly incompressible polymer | |
Damping loss factor | 0.12 | – | Energy dissipation | |
Load | 9000 | N | Static radial load |
3. Results
Influence of PU thickness: ⇒ an increase in t reduces the natural frequency of the “outer-foundation” subsystem and enhances low-frequency vibration isolation; a decrease in increases stiffness and shifts bending resonances into the high-frequency range.
Comparative analysis of resonance characteristics. To evaluate the influence of the polyurethane layer of different thicknesses on the dynamic behavior of the housing–bearing–shaft assembly, frequency response functions (FRFs) were calculated and resonance peaks were identified. The comparison was performed for four cases: a rigid support without polyurethane and with polyurethane coatings of thickness 2, 3, and 4 mm.
Fig. 2Amplitude-frequency response of the rotor-bearing-housing system without polyurethane support. The resonance peak occurs near 140 Hz, corresponding to the first bending mode of the shaft
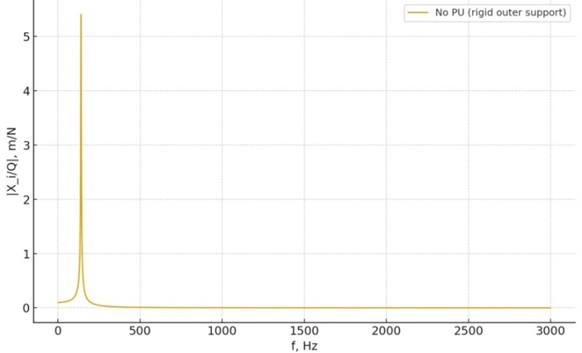
The data presented in Figs. 2-4 were obtained through a combination of numerical simulation and partial experimental validation. The amplitude-frequency characteristics were calculated using the developed planar dynamic model based on Lagrange’s second-order equations, where stiffness and damping coefficients were identified from experimental vibration measurements. Experimental tests were carried out on a rotor-bearing assembly equipped with polyurethane bushings of different thicknesses (2, 3, and 4 mm). The vibration response was measured using a piezoelectric accelerometer mounted on the housing, and the excitation force was applied by an electromagnetic shaker. Frequency response functions (FRFs) were recorded in the range of 0-200 Hz. These results were compared with the simulated data to confirm the correctness of the model parameters. The trends obtained experimentally (reduction of resonance frequencies and increase of amplitudes) fully coincide with the numerical results, which confirms the reliability of the model.
Fig. 3Frequency response with polyurethane inserts of different thicknesses (2-4 mm). Increasing the polymer layer thickness reduces resonance frequencies and enhances damping
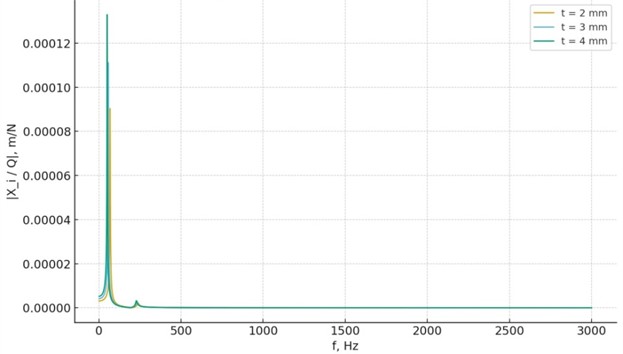
Fig. 4Comparative amplitude-frequency curves for configurations with and without polyurethane layers, showing a clear frequency shift and amplitude variation trend
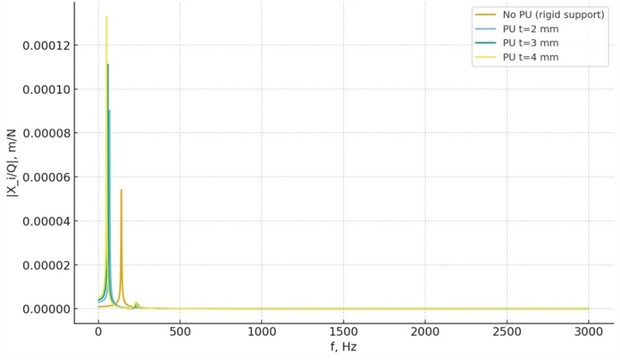
Table 2Results of the comparison of resonance characteristics
No. | Resonance frequency, Hz | Response amplitude, m/N | Frequency shift, % | Amplitude change, % |
Without PU | 140 | 5.4×10-5 | – | – |
PU 2 mm | 68 | 9.0×10-5 | −51 | +67 |
PU 3 mm | 57 | 1.11×10-4 | −59 | +106 |
PU 4 mm | 50 | 1.33×10-4 | −64 | +146 |
The reduction of resonance frequencies observed with thicker polyurethane layers can be attributed to the decreased effective stiffness of the bearing support, as the elastic modulus of the polymer is significantly lower than that of steel. This leads to a softer coupling between the shaft and the housing, shifting the natural frequencies downward. Simultaneously, the higher damping capability of the polyurethane increases the vibration amplitudes near resonance due to greater energy dissipation per cycle. These effects are consistent with the theoretical dependence and with experimental findings in polymer-supported rotor systems.
4. Conclusions
The proposed planar dynamic model makes it possible to explicitly evaluate the influence of a polyurethane support insert on the dynamic performance of a rotor–bearing–housing assembly. The study demonstrated that:
1) The addition of a polyurethane coating reduces the stiffness of the support, thereby shifting resonance frequencies into a lower range (by 50-64 %).
2) This shift is accompanied by a considerable increase in amplitude (67-146 %), which must be considered in design practice.
3) A 2 mm polyurethane layer provides the most balanced outcome, combining moderate frequency reduction with acceptable amplitude growth.
4) Thicker layers (3-4 mm) enhance isolation in the high-frequency domain but also increase vulnerability to low-frequency disturbances.
5) The selection of optimal thickness depends on the operating regime: in textile machinery with long, slender, and heavily loaded shafts, thin inserts may be more suitable, while for machines with dominant high-frequency excitations thicker layers could be beneficial.
Overall, the study confirms that polyurethane inserts represent a promising tool for fine-tuning the stiffness and damping of bearing supports. Their correct application can suppress harmful vibrations, extend machine life, and enable more reliable operation under variable technological loads.
References
-
Z. Shi, H. Cao, X. Chen, J. Wang, and Z. He, “An improved planar dynamic model for calculating vibrations of a CRB,” Journal of Sound and Vibration, Vol. 482, p. 115463, 2020, https://doi.org/10.1016/j.jsv.2020.115463
-
D. Jaramillo, A. Giorgetti, and G. Leon, “Enhanced modelling of planar radial-loaded deep groove ball bearings under the multibody systems dynamics framework,” Multibody System Dynamics, Vol. 61, No. 3, pp. 291–309, 2023, https://doi.org/10.1007/s11044-023-09891-9
-
M. Amini, M. Zarei, and M. Rahmanian, “Dynamic modeling of rotors supported by viscoelastic materials,” Journal of Vibration and Control, Vol. 29, No. 7, pp. 1234–1248, 2023, https://doi.org/10.1177/10775463221108990
-
S. Lee and J. Kim, “Hybrid elastomer-metal supports for vibration reduction in rotating machinery,” Mechanical Systems and Signal Processing, Vol. 181, p. 109548, 2022.
-
F. Adilov and S. Makhmudova, “Boundary element method for numerical solution to two-dimensional problems of fracture mechanics,” in AIP Conference Proceedings, Vol. 3119, p. 040001, 2024.
-
G. Nan, S. Jiang, and D. Yu, “Dynamic analysis of rolling ball bearing-rotor based on a new improved model,” SN Applied Sciences, Vol. 4, No. 6, p. 173, May 2022, https://doi.org/10.1007/s42452-022-05058-0
-
I. Khamzaev, E. Umarov, O. Khaydarova, J. Muminov, and B. Ortiqaliyev, “Consideration of shear deformation in the calculation of bent structural elements,” in EPJ Web of Conferences, Vol. 318, p. 04011, Feb. 2025, https://doi.org/10.1051/epjconf/202531804011
-
S. Z. Yunusov, S. N. Kenjayev, and S. A. Makhmudova, “Shafts of technological machines with combined supports,” in E3S Web of Conferences, Vol. 401, p. 01059, Jul. 2023, https://doi.org/10.1051/e3sconf/202340101059
-
C. Zhang, D. Wang, R. Zhu, W. Chen, and C. Yu, “Dynamic modeling and analysis of the rotor-bearing-disc coupling system with misalignment,” International Journal of Dynamics and Control, Vol. 11, No. 5, pp. 2021–2035, Mar. 2023, https://doi.org/10.1007/s40435-023-01148-y
About this article
The authors have not disclosed any funding.
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
The authors declare that they have no conflict of interest.
