Miniature rotary tables with piezoelectric hemispheres: research and development

1. Introduction

Piezoelectric hemisphere actuators are characterized by specific features, which are mainly used in underwater acoustics devices used as ultrasonic transmitters or receivers [1, 2], in seismic physical modelling systems and oscillatory transducers in experiments simulating seismic surveys on land or sea [3, 4] or in piezoelectric ceramic electromechanical transducers, utilizing axisymmetric oscillations of complete and incomplete spherical shells [5]. Lately the area of their applications expanded, comprising hemispherical tilt stages driven by stick-slip motion [6] or positioning on the plane devices [7, 8], in which the main accent of investigation was placed on generating the modes of oscillation that can be employed in the design of multimode unidirectional electroacoustic transducers and on determining the electrode configurations that achieve optimal electromechanical coupling for the different modes of oscillation [5, 8]. These modes of oscillations – asymmetric modes – can be generated in hemisphere actuators by sectioning the electrodes into several parts and connecting to some of them harmonic signal (standing wave mode) or harmonic signals with special phase shift (traveling wave mode). As a result, specific points of hemisphere actuators are effecting 3D trajectories and their synthesis is the main aim of investigation.

2. Trajectories and node points in hemisphere transducers

Theoretical and experimental investigations, especially using modern methods of holographic interferometry, enabled to select optimal forms and modes of oscillation, taking into account the position of contact zones and specifics of fixing the transducer in the oscillation nodes. Finite element method was used to perform modal frequency and harmonic response analysis and to calculate trajectories of the driven tips movements [9]. Basic dynamic equation of the piezoelectric hemisphere are derived from the principle of minimum potential energy by means of variational functionals and for piezoelectric actuator can be written as follows [9]:

where $\left[M\right]$, $\left[K\right]$, $\left[T\right]$, $\left[S\right]$, $\left[C\right]$ are matrices of mass, stiffness, electro elasticity, capacity, damping respectively, $\left\{u\right\}$, $\left\{F\right\}$, $\left\{Q_1\right\}$ are vectors of nodes structural displacements, external mechanical forces, and charges coupled on the electrodes, $\left\{{\varphi }_1\right\}$, $\left\{{\varphi }_2\right\}$ are vectors of nodal potentials of the nodes associated with electrodes and vector of nodal potentials calculated during numerical simulation [9]. Mechanical and electrical boundary conditions can be applied to piezoelectric hemisphere i. e. mechanical displacement of the fixed surfaces of the actuator are equal to zero and electric charge of piezoelements that are not coupled with electrodes are equal to zero too.

Natural frequencies and modal shapes of the hemisphere (Fig. 1) are derived from the modal solution of the piezoelectric system:

where $K^{*}$ is modified stiffness matrix. In case when $\left\{Q_1\right\}=\text{0}$ it can be written as follows:

Fig. 1Hemisphere piezoelectric transducer: a) General view, b) The distribution of electrodes 1, 2 and 3 (in case when number of sections is equal to 3)

a)

b)

Traveling wave type of oscillations were realized by connecting the electrodes 1, 2 and 3 to signal generator (3 harmonic signals with shifted phase by 120°). Another possibility is to use different sectioning of electrodes (Fig. 2(a)) and applying just one harmonic signal; in this case (Fig. 2(b)) four different phases of harmonic signal are realized – with 0°, 90°, 180° and 270° phase shifts.

Fig. 2Generating traveling wave oscillations in the hemisphere transducer, symmetrical in relation to its axis

a)

b)

For modelling industrial software programme COMSOL Multiphysics, based on FEM were used. The dimensions of piezoceramic hemisphere (material – PZT-8) were: external diameter $D=$0,04 m, internal diameter $d=$ 0,037 m, hight – 0,01 m. Three contacting points were applied ($d_c=$ 0,003 m and hight $h_c=$0.002 m, material – high friction composite XRT-12).

Fig. 3FEM model of hemisphere transducer: a) Side view, b) Bottom view

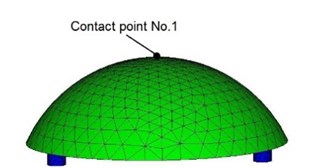
a)

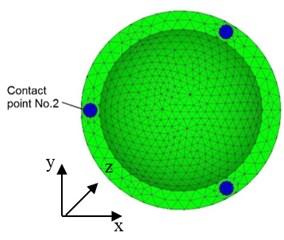
b)

The aim of modeling was to find resonant frequencies and amplitudes of traveling wave in three directions (along coordinates $x$, $y$ and $z$) and establish trajectories of contacting points. 40 V three harmonic electric signals were applied to the electrodes of the transducer with 2/3$\pi$ phase shift. The range of frequency control was 45…65 kHz with 200 Hz steps. Fig. 4 illustrates results of numerical simulation where amplitude – frequency function and elliptical trajectories of contact points No. 1 and No. 2 are presented. It can be seen that amplitude peaks are obtained at the resonant frequencies 53.0 kHz and 63.0 kHz. Trajectories of both contact points are shown in Fig. 4(c). It can be noticed that trajectories have ellipsoidal shapes. Direction of contact points motion is opposite at the frequencies 53.0 kHz and 63.0 kHz. Ratio between major and minor axes of the ellipses varies depending of excitation frequency.

Fig. 4Characteristics of piezoelectric hemisphere transducer in case when all 3 electrodes are activated in traveling wave mode: a) Amplitude – frequency function of point No. 1 (Fig. 3); b) Amplitude – frequency characteristics of point No. 2; c) Elliptical trajectories of contacting points No. 1 and No. 2

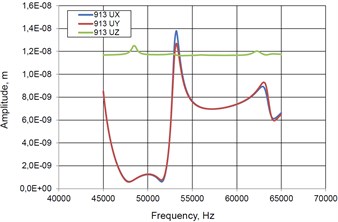
a)

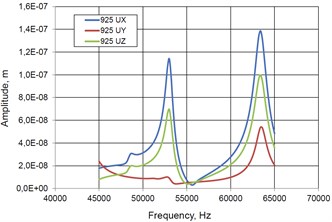
b)

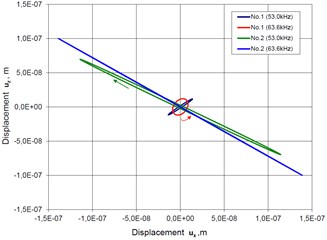
c)

3. Two modifications of piezoelectric rotary tables

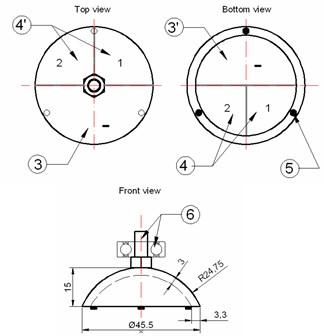
First modification is shown in Fig. 1 and presents small diameter (18 mm) rotary table with external encoder, aimed at using as high resolution additional source of movement for microscopes. Table contains piezoelectric hemisphere transducer, manufactured by Morgan Technical Ceramics (MTC ElectroCeramics, Bursledon Road, Thornhill, Southampton, SO19 7TG, England) with outside diameter 15mm and wall thickness 1mm. Contact of hemisphere transducer with encoder is realized with the help of three pads, made from high friction plastic. Radial position (centering) of the table is ensured by sliding bearing and initial preload is guaranteed by controlling the gap $\mathrm{\Delta }$ between permanent magnet and ferromagnetic disk 3 (Fig. 5). As can be seen from Fig. 1, the design of the table is simple and the cost is very low.

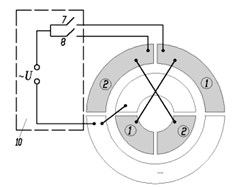
Fig. 5Miniature rotary table with piezoelectric hemisphere transducer, oscillating in traveling wave mode: a) Schematic (1 – hemisphere transducer, 2 – three contacting points, made from high friction material, 3 – ferromagnetic axis, 4 – permanent magnet – sliding bearing, 5 – rotating table with rotary position encoder, 6 – elastic support, 7, 8, 9 – electrodes); b) General view; c) Disassembled view

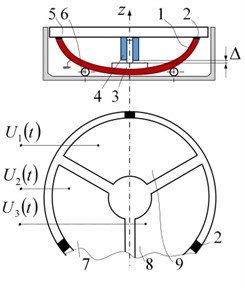
a)

b)

c)

Fig. 6Rotary table with low height/diameter rate: a) General view; b) Disassembled view (general schematics corresponds to Fig. 5(a)); c) Harmonic signal generators, supplying three-phase voltage and measuring amplitude/phase – frequency characteristics

a)

c)

b)

The same schematic is used in another rotary table (Fig. 6), where piezoelectric hemisphere (outside diameter 54 mm; wall thickness 2.7 mm) ensures low height/diameter rate of the table.

Fig. 7Resolution of rotary table (Fig. 6) with low height/diameter rate: a) At frequency 32.1 kHz, amplitude 80 V (burst of 5 cycles with period of 1 sec) and b) Trajectory of contacting point

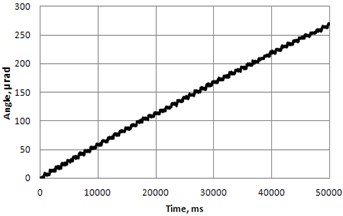
a)

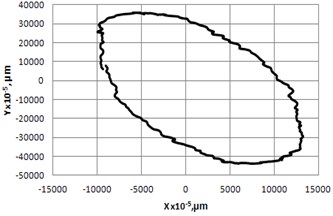
b)

Fig. 8Frequency response in vertical a) and lateral b) directions

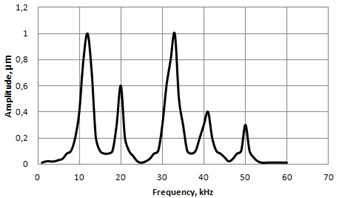
a)

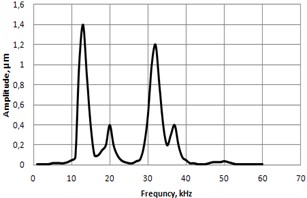
b)