Research on optimum design of temperature-vibration accelerated storage test plan

2.1. The failure distribution function

Under the impact of environmental stresses during the long storage period, the life distribution of electronic equipment obeys Weibull distribution [9], denoted as Weibull ($m$, $\eta$).

2.2. Accelerated model

The general Eyring model [10], which is applicable to the condition where the failure is caused by temperature stress and vibration stress at the same time, can be represented as follows:

where, $t_L$ denotes characteristics of products; $E_a$ is activation energy, usually in electron-volts; $k$ stands for the Boltzmann’s constant; $T$ represents the absolute Kelvin temperature; $S$ represents vibration strength (unit: g²/Hz); $A$ and $B$ are parameters to be estimated, $B<$0.

Taking logarithm function on both sides, let ${\theta }_0=\mathrm{l}\mathrm{n}A\text{,}$${\theta }_1=Ea/1000k\text{,}$$x=1000/T\text{,}$${\theta }_2=B\text{,}$$y=\mathrm{l}\mathrm{n}H$ the distribution parameters of product lifetime is the function of stress $x$ and $y$, namely:

4.1. Likelihood function of censored samples

In order to simplify the formula, let $\delta =\mathrm{l}\mathrm{n}t$, the Weibull distribution can be transformed to extreme value distribution. Its probability density function is:

where, $\mu =\mathrm{l}\mathrm{n}\eta$. For $i$th test specimen, the failure time under stress combination is ${\delta }_i$. Then:

Therefore, the likelihood function of $i$th test specimen can be denoted as follows:

Let $z_i=({\delta }_i-\mu )/\sigma \text{,}{\xi }_i=({\tau }_i-\mu )/\sigma$, where, $\mu ={\theta }_0+{\theta }_1{x}_i+{\theta }_2{y}_i$. The likelihood function of the whole test sample can be represented as follows:

4.2. Fisher information matrix and covariance matrix

According to the maximum likelihood estimation theory, the variance and covariance matrix of model parameter estimates can be presented as:

where, $\mathbf{\Sigma }$ is the inverse matrix of information matrix, namely, $\mathbf{\Sigma }={\mathbf{F}}^{-1}$. While, the information matrix is the expectation of likelihood function’s negative second order partial derivative matrix. Combined with Eq. (10), there is:

where, $A_{ij}$ is mathematical expectation of parameters ${\theta }_0\text{,}{\theta }_1\text{,}{\theta }_2\text{,}\sigma$.

5.1. Objective function

Assuming that temperature stress levels and vibration stress levels are both $k$, which satisfies $T_1>T_2\dots >T_k$, $S_1>S_2\dots >S_k$. And test sample is $n$. According to uniform design theory, the SDSAST only need to be conducted $k$ steps [12]. For linear extremum model, under the stress combination $x_i\text{,}$$y_j\text{,}$ the $P_{th}$ order quantile of product life distribution is ${\widehat{g}}_P(x_0,y_0)={\widehat{\theta }}_0+{\widehat{\theta }}_{1}x+{\widehat{\theta }}_{2}y+z_P\widehat{\sigma }$ [13]. When $P=$0.5, $z_p=$–0.3665, the $P_{th}$ order quantile ${\widehat{g}}_P(x_0,y_0)$ of product lifetime is the product’s median life [2]. Under the normal stress level combination $x_0\text{,}$$y_0\text{,}$ the asymptotic variance can be represented as:

Regarding the minimum asymptotic variance of normal stress level combination as objective function, namely solving $\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{V}\mathrm{a}\mathrm{r}\left[{\widehat{g}}_P\right(x_0,y_0\left)\right]$ [14].

5.2. Selection of design variables

Now that the maximum temperature stress level, the highest vibration stress level, normal temperature and vibration stress level are all given, the $P_{th}$ order quantile estimates of normal life distribution only depends on the rest two groups of $k$-1 stress levels and failure time considering stress accumulation effect, namely, the optimization design variables are mainly $T_1>T_2\dots >T_k$, $S_1>S_2\dots >S_k$, and accumulation failure time $t_1({\theta }_1,{\theta }_2)$, $t_2({\theta }_1,{\theta }_2)$,…, $t_r({\theta }_1,{\theta }_2)$.

5.3. Constraint conditions

1) Stress level: Before stress combination, temperature stress levels must satisfy $T_1>T_2\dots >T_k$ and vibration stress levels must satisfy $S_1>S_2\dots >S_k$.

2) In order to guarantee a certain acceleration effect, the acceleration factor ${\alpha }_{i~0}$ of all levels relative to normal stress level must be bigger than a certain value, namely: ${\alpha }_{i~0}=\mathrm{e}\mathrm{x}\mathrm{p}\left\{{\theta }_1\left(x_0-x_i\right)+{\theta }_2\left(y_0-y_i\right)\right\}\ge {\alpha }_{min}={\eta }_0/{\eta }_i$ and $a_{1~0}>a_{2~0}>\dots >a_{k~0}\text{,}$$i=1,\dots ,k$.

3) The combination of temperature and vibration stress should satisfy uniform design table.

5.4. Optimization model

Summing up conditions above, the mathematical model of multi-stress ALT optimization design scheme can be concluded as follows:

6.1. Multi-stress accelerated storage test optimization design of an electric connector

6.2. Monte-Carlo simulation and verification

In order to illustrate the rationality of optimization scheme, 100 groups of experimental data are generated employing Monte-Carlo to simulate each accelerated storage test schema.

Fig. 1Minimum asymptotic variance value volatility of each program

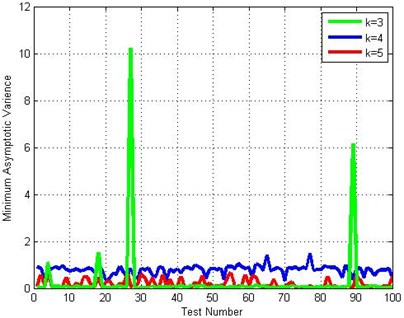
Fig. 2Minimum asymptotic variance mean value volatility of each program

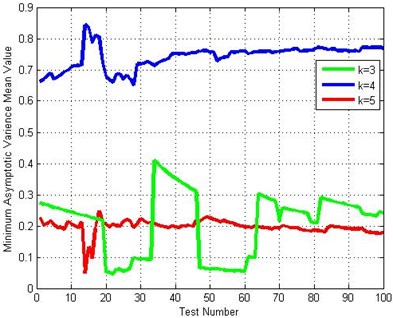
Drawing the variation tendency figure of the minimum asymptotic variance and the minimum asymptotic variance mean value changing with experiment times, which are shown as Fig. 1 and Fig. 2. From Fig. 1, it is easy to see that the asymptotic variance of median life is minimum when $k=$ 5. From Fig. 2, we see that the minimum asymptotic variance mean value is maximum when $k=$4, median when $k=$ 3, but has a bigger fluctuation. While the minimum asymptotic variance mean value is minimum when $k=$ 5 and has a smaller fluctuation. In conclusion, the combination scheme is optimal when $k=$5 in the combination schemes.