Energy efficiency of passive vibroisolation in machines and devices

Dobry, Marian Witalis

Vibroengineering Procedia

Browse Procedia

Published: 10 October 2014

Check for updates

Energy efficiency of passive vibroisolation in machines and devices

Marian Witalis Dobry¹

¹Poznan University of Technology, Institute of Applied Mechanics, Poznan, Poland

Cite the article Download PDF

Downloads 1099

Abstract

The article describes a new method of evaluating vibroisolation efficiency in terms of power distribution of structural forces. It reports results of a study of power distribution of structural forces in a mechanical system with one degree of freedom. The analysis uses the First Principle of Power Distribution in a Mechanical System to obtain a distribution of input power into three kinds of powers: the power of inertia, the power of dissipation and the power of elasticity. The sum of these three kinds of powers gives the total power introduced into the mechanical system by the driving force. RMS values of the three kinds of power and the total power were computed depending on a dimensionless frequency in the range from 0 to 5. They were then used to calculate the value of the function of energy efficiency of passive vibroisolation defined as a ratio of total power introduced into the system by the driving force to the power of elasticity depending on the dimensionless frequency. The study revealed that vibroisolation is efficient when the value of energy efficiency exceeds 11.8.

1. Introduction

So far the efficiency of passive vibroisolation has been determined in the amplitude domain with respect to forces (force vibroisolation) or displacements (displacement vibroisolation). Its value, calculated for specific conditions of the driving force and dynamic parameters of the mechanical system, represents the degree of reduction in force or displacement amplitudes after passing through the vibroisolation system.

The efficiency of vibroisolation is the inverse of transmissibility, whose value shows what part of amplitudes of the force or displacement in the source is transmitted to the protected equipment [1-6].

The present article discusses the efficiency of vibroisolation using a new approach. The efficiency of vibroisolation is defined in the power domain based on calculations of the distribution of the input power of the driving force into the powers of resistance resulting from inertia, dissipation and elasticity, which are generated in the elementary mechanical system. By defining the efficiency of vibroisolation in the power domain, it is possible to account not only for the value of forces and displacements but also the system’s operating speed [7, 8].

2. The classic definition of vibration isolation efficiency

The classic approach to calculating vibration isolation efficiency of a mechanical system with one degree of freedom is to determine the inverse of transmissibility using the following formula:

1

E F_{v i b r o i s o l a t i o n} = \frac{R_{b a s e}}{F_{r e d . a m p l .}} = \frac{Z_{0}}{A_{0}} = \sqrt{\frac{(1 - δ^{2})^{2} + 4 ξ^{2} δ^{2}}{1 + 4 ξ^{2} δ^{2}}},

where:

2

δ = \frac{ω_{w}}{ω_{0}} = \frac{f_{w}}{f_{0}} = ω_{w} \sqrt{\frac{m_{z}}{k_{z}}} = 2 π f_{w} \sqrt{\frac{m_{z}}{k_{z}}},

dimensionless frequency of vibrations in a mechanical system, $ω_{w}$ and $f_{0}$ – circular frequency in rd/s and frequency in Hz of the driving force, $ω_{0}$ and $f_{0}$ – circular frequency in rd/s and frequency in Hz of undamped free vibrations, $ξ = \frac{c_{z}}{2 \sqrt{m_{z} k_{z}}}$ – the degree of damping in a mechanical system, $m_{z}$ – reduced, equivalent mass coefficient, $c_{z}$ – reduced, equivalent damping coefficient, $k_{z}$ – reduced, equivalent elasticity coefficient.

The degree of damping in vibration isolation systems should be low, since damping in the range of frequencies related to effective vibroisolation is not desirable. The most commonly accepted value is 0.1. Fig. 1 shows the function of vibroisolation efficiency for two values of the degree of damping $ξ_{1} =$ 0.01 and $ξ_{2} =$ 0.1. With respect to vibroisolation at $δ > \sqrt{2}$ , the efficiency of vibroisolation is greater for a lower degree of damping, which confirms the validity of the above postulate – see Fig. 1.

Introducing small damping in vibration isolation systems is desirable, although it decreases vibroisolation efficiency. The decrease is not significant and the mechanical system becomes more stable. Moreover, the use of small damping decreases the amplification of the amplitude of reaction forces of the foundation or vibratory displacements of the protected equipment in the frequency range below $δ <$ 1.41, i.e. at the below-resonant and resonant frequency – Fig. 1. In this range, damping also has a positive effect on reducing dynamic stress in elastic elements, especially when the system is passing through resonant frequency during start-up and coast-down.

Fig. 1The efficiency of passive vibroisolation as a function of dimensionless frequency δ and degree of damping ξ determined in the amplitude domain of forces and displacements

The efficiency of passive vibroisolation as a function of dimensionless frequency δ and degree of damping ξ determined in the amplitude domain of forces and displacements

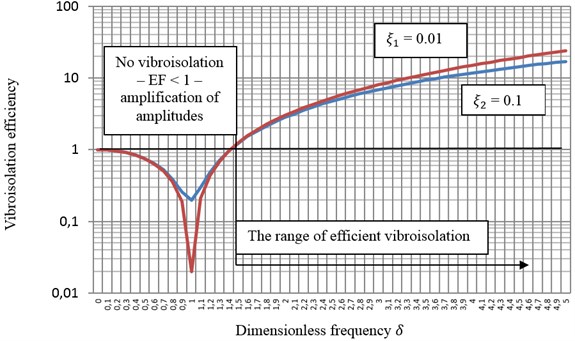
After analyzing the function of vibroisolation efficiency for a mechanical system with one degree of freedom Eq. (1) it is evident that efficiency is strongly dependent on the value of dimensionless frequency $δ$ . Its value, in turn, depends, according to Eq. (2), on the ratio of the frequency of the driving force to the frequency of undamped free vibrations $ω_{0}$ in a mechanical system, which is a characteristic of an elastically connected damper (vibroisolation) of the protected equipment. In the frequency range of $δ$ less than $\sqrt{2}$ negative values of vibroisolation efficiency are obtained, which results in the amplification of forces and displacements affecting the protected equipment.

In order to move to the domain of power distribution in the dynamic structure of mechanical systems it was necessary to define energy-related quantities, which would provide a holistic description of the vibroisolation properties of vibration isolation [7, 8].

3. Energy efficiency of vibroisolation as a new method of its assessment

This article presents a new approach to determining the efficiency of vibroisolation in a mechanical system in a new domain, namely power distribution and energy flow in its dynamic structure.

The theoretical basis for power distribution in the dynamic structure of a mechanical system is provided by the First Principle of Power Distribution in a Mechanical System, first formulated in 1998 [7, 8]. It states: „The net input power introduced into the mechanical system (after subtracting the power of dissipation) is equal to the reflected power (accumulated or stored) in the system and the output power generated by the system”. It can be expressed mathematically as the equation of momentary power:

3

P_{i n} (t) - P_{l o s s} (t) = P_{r e f} (t) + P_{o u t} (t),

where: $P_{i n} (t)$ – input power introduced to a mechanical system, $P_{l o s s} (t)$ – the power of dissipation in a mechanical system, $P_{r e f} (t) = P_{i n e r t .} (t)$ + $P_{e l a s t .} (t)$ – reflected power in a mechanical system, $P_{i n e r t .} (t)$ – the power of inertia in a mechanical system, $P_{e l a s t} (t)$ – the power of elasticity in a mechanical system, $P_{o u t} (t)$ – output power of a mechanical system.

By applying the principle to a mechanical system with one degree of freedom, the following equation of power can be derived:

4

F_{i n} (t) \dot{x} (t) - c {[\dot{x} (t)]}^{2} = m \ddot{x} (t) \dot{x} (t) + k x (t) \dot{x} (t) + F_{o u t} (t) \dot{x} (t) .

In the case of vibroisolation of free mass „ $m$ ” excited by force $F_{i n} (t)$ , input power $P_{o u t} (t)$ is equal to 0, since the foundation is motionless and its velocity is equal to 0. In this case, the equation of power can be transformed into Eq. (4a):

4a

F_{i n} (t) \dot{x} (t) - c {[\dot{x} (t)]}^{2} = m \ddot{x} (t) \dot{x} (t) + k x (t) \dot{x} (t) .

Subjecting Eq. (4a) to further transformations, i.e. dividing by input power and multiplying by 100 %, one arrives at Eq. (5) expressing the percentage distribution of power in the dynamic structure of a mechanical system with vibration isolation, in the following form:

5

\frac{m \ddot{x} (t) \dot{x} (t)}{F_{i n} (t) \dot{x} (t)} 100 + \frac{c {[\dot{x} (t)]}^{2}}{F_{i n} (t) \dot{x} (t)} 100 + \frac{k x (t) \dot{x} (t)}{F_{i n} (t) \dot{x} (t)} 100 = 100 [%] .

Given the equality of input power to the sum of individual powers, Eq. (5) can be expressed as Eq. (6):

6

\frac{m \ddot{x} (t) \dot{x} (t)}{\{m \ddot{x} (t) \dot{x} (t) + c {[\dot{x} (t)]}^{2} + k x (t) \dot{x} (t)\}} 100 + \frac{c {[\dot{x} (t)]}^{2}}{\{m \ddot{x} (t) \dot{x} (t) + c {[\dot{x} (t)]}^{2} + k x (t) \dot{x} (t)\}} 100

+ \frac{k x (t) \dot{x} (t)}{\{m \ddot{x} (t) \dot{x} (t) + c {[\dot{x} (t)]}^{2} + k x (t) \dot{x} (t)\}} 100 = 100 [%] .

In order to calculate percentage shares of individual types of power changing over time, their RMS values were calculated. This can be expressed as Eq. (7). The equation can be simplified as Eq. (8) using substitute symbols.

Fig. 2 shows curves representing the percentage distribution of RMS values of three types of powers calculated for a system with one degree of freedom as a function of dimensionless frequency $δ$ . They were calculated for a mechanical system, assuming the following parameters: $m =$ 15 [kg], $ξ =$ 0.1, $k =$ 5000 [N/m], $F (t) = 200 s i n [(2 π f_{w}) t]$ [N], $δ$ in the range from 0 to 5.

By analysing the curves representing the percentage distribution of individual types of power as a function of dimensionless frequency, one can explain the phenomenon of power distribution in a dynamic structure of a mechanical system:

7

\frac{\sqrt{\frac{1}{t} \int_{0}^{t} {[m \ddot{x} (t) \dot{x} (t)]}^{2} d t}}{\{\sqrt{\frac{1}{t} \int_{0}^{t} {[m \ddot{x} (t) \dot{x} (t)]}^{2} d t} + \sqrt{\frac{1}{t} \int_{0}^{t} {\{c {[\dot{x} (t)]}^{2}\}}^{2} d t} + \sqrt{\frac{1}{t} \int_{0}^{t} {[k x (t) \dot{x} (t)]}^{2} d t}\}} 100

+ \frac{\sqrt{\frac{1}{t} \int_{0}^{t} {\{c {[\dot{x} (t)]}^{2}\}}^{2} d t}}{\{\sqrt{\frac{1}{t} \int_{0}^{t} {[m \ddot{x} (t) \dot{x} (t)]}^{2} d t} + \sqrt{\frac{1}{t} \int_{0}^{t} {\{c {[\dot{x} (t)]}^{2}\}}^{2} d t} + \sqrt{\frac{1}{t} \int_{0}^{t} {[k x (t) \dot{x} (t)]}^{2} d t}\}} 100

+ \frac{\sqrt{\frac{1}{t} \int_{0}^{t} {[k x (t) \dot{x} (t)]}^{2} d t}}{\{\sqrt{\frac{1}{t} \int_{0}^{t} {[m \ddot{x} (t) \dot{x} (t)]}^{2} d t} + \sqrt{\frac{1}{t} \int_{0}^{t} {\{c {[\dot{x} (t)]}^{2}\}}^{2} d t} + \sqrt{\frac{1}{t} \int_{0}^{t} {[k x (t) \dot{x} (t)]}^{2} d t}\}} 100

= 100 [%],

8

\frac{P_{i n e r t} (R M S)}{P_{T} (R M S)} 100 + \frac{P_{l o s s} (R M S)}{P_{T} (R M S)} 100 + \frac{P_{e l a s t} (R M S)}{P_{T} (R M S)} 100 = 100 [%],

where: $P_{T} (R M S) = P_{i n e r t} (R M S) + P_{l o s s} (R M S) + P_{e l a s t} (R M S) - R M S$ value of total input power introduced into the mechanical system by the driving force equal to the sum of RMS values of individual types of power.

Fig. 2Distribution of individual types of power (RMS) in the dynamic structure of a mechanical system with passive vibroisolation as a function of dimensionless frequency δ

Distribution of individual types of power (RMS) in the dynamic structure of a mechanical system with passive vibroisolation as a function of dimensionless frequency δ

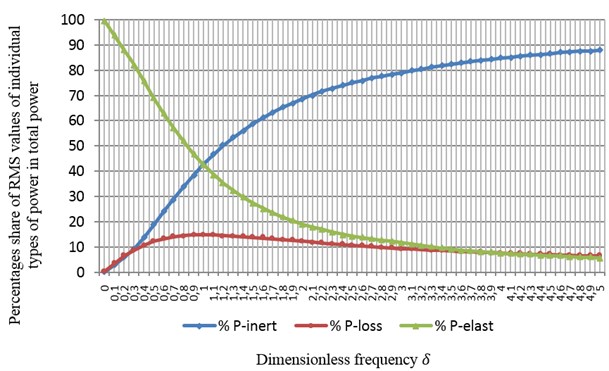
At frequency close to 0, the share of the power of elasticity is nearly 100 %, which implies that the whole power of the driving force is used to overcome the restoring force of the vibroisolation system. The power of elasticity of the vibroisolation system can be an energy measure of the power level that elastic elements are subjected to. As frequency $δ$ of the driving force increases, so does the power of inertia and dissipation in the system. The power of elasticity, in contrast, declines monotonically in the range of under-resonant frequencies $δ < 1$ .

At frequency $δ$ equal to 1, the power of elasticity reaches the same level as the power of inertia, while the power of dissipation reaches its peak. It is the resonant frequency of a mechanical system mounted on a vibroisolation system. In this particular example, at resonant frequency, the first two types of power reach 42.5 % of input power, while the power of dissipation reaches a maximum value of 15 %.

From the point of intersection of between the curves showing the percentage share of the power of elasticity and inertia, the share of the power of elasticity continues to decrease monotonically, while the share of the power of inertia increases. This implies that the amount of power transferred to elastic elements declines, while the power of inertia increases, constituting the main component of the dynamic resistance in the frequency range $(1, \infty)$ . The higher the frequency is, the lower the power of elasticity. For the value of $δ =$ 5 in Fig. 1, the power of elasticity accounts for only 5.7 % of total input power. This means that vibroisolation systems characterised by a high value of dimensionless frequency $δ$ can achieve high efficiency of vibration isolation.

The power of dissipation also declines monotonically starting from (resonant) frequency $δ =$ 1 and tends to 0 for $δ = \infty$ .

Knowing the energy phenomena occurring in the dynamic structure of a mechanical system with vibroisolation, vibroisolation efficiency can be defined in a number of ways. One of them is presented below.

The value of vibroisolation efficiency of isolation systems in mechanical systems can be determined on the basis of the ratio of RMS input power introduced into a mechanical system with vibroisolation to the RMS power of elasticity, which is an energy measure of the power flowing through the support (elastic) structure of a mechanical system. Adopting this definition, energy efficiency of vibroisolation ( $E E_{v i b r o i s o l a t i o n}$ ) can be expressed as:

9

E E_{v i b r o i s o l a t i o n} = \frac{P_{T} (R M S)}{P_{e l a s t} (R M S)} .

Its value describes how much the power of the restoring force is smaller than the total input power introduced into a mechanical system with vibroisolation by the exciting force. The higher its value, the greater the efficiency of the vibroisolation system designed to reduce the impact of vibration on the elastic elements of support structure of the protected equipment.

4. Results

The results of calculating energy efficiency of the passive vibroisolation system for parameters given above expressed as a function of dimensionless frequency $δ$ are presented in Fig. 3. The value of energy efficiency for frequencies close to is equal to 1. This means that the whole power of the exciting force is absorbed by forces of elasticity, with the same amount of power.

Fig. 3Energy efficiency of a vibroisolation system depending on dimensionless frequency of vibrations in a mechanical system, for degree of damping ξ= 0.1

Energy efficiency of a vibroisolation system depending on dimensionless frequency of vibrations in a mechanical system, for degree of damping ξ= 0.1

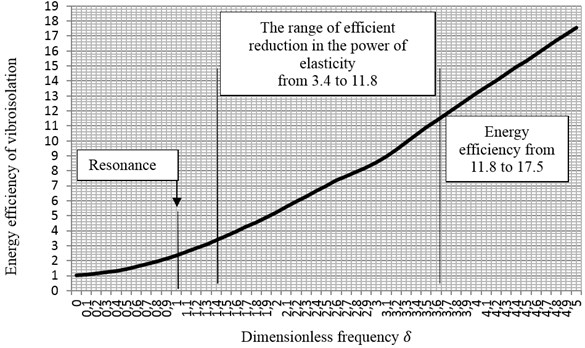
As frequency increases, so does the efficiency of energy vibroisolation. At frequency $δ =$ 1, that is at the resonant frequency of the mechanical system, the efficiency of vibroisolation, defined by Eq. (9) equals 2.3. This corresponds to a 2.3-fold decrease in the value of forces of elasticity. It should be noted that this value refers to the total power introduced into the mechanical system by the driving force.

After passing through the mechanical resonance of the system, the efficiency of energy vibroisolation continues to grow monotonically. At frequency $δ =$ 3.7, when the reduction in forces and displacement amplitudes reaches the value of 10, energy efficiency amounts to 11.8.

Energy-related assessment of the reduction in forces (force vibroisolation) or displacements (displacement vibroisolation) indicates that efficient vibroisolation used in practice starts when the power of the driving force is reduced 11.8 times after passing through the vibroisolation system. Consequently, the amount of power transferred to the elastic elements of the system is 11.8 times smaller in relation to the power of the input force.

Energy efficiency defined in the power domain with respect to forces acting in a mechanical with vibroisolation system can be described as the efficiency of reducing the power in a vibroisolation system, comparing the power of the source with the power of elasticity, which characterizes the power absorbed by elastic elements of the support structure of the passive vibroisolation system.

When one compares vibroisolation efficiency defined in the domain of force or displacement amplitudes shown in Fig. 1 with vibroisolation efficiency defined in Eq. (9) above, it can be noticed that a reduction in the force impact on the foundation in a mechanical system with vibroisolation will become evident when the power of elasticity is 3.4 smaller than the power of the exciting force. From that moment onwards, at $δ =$ 1.41, the reduction in the impact of vibration will continue to increase with growing energy efficiency of the system in question. For energy efficiency of 11.8, the reduction in the force impact on the foundation will be equal to 10. This corresponds to $δ =$ 3.7.

A system of passive vibroisolation with this kind of performance can be regarded as efficient. Increasing dimensionless frequency will further improve the efficiency of force and energy vibroisolation. At frequency $δ =$ 5 the efficiency of force vibroisolation equals 17, while the efficiency of energy vibroisolation is equal to 17.5.

5. Conclusions

Based on an energy analysis of a mechanical system with one degree of freedom with vibroisolation, the following conclusions can be drawn:

1) Energy analysis of the power distribution in the dynamic structure of the system in question helps to explain the phenomenon of power distribution as a function of dimensionless frequency $δ$ and degree of damping $ξ$ .

2) The structural power distribution in a mechanical system with vibroisolation with one degree of freedom depends, above all, on dimensionless frequency $δ$ .

3) The percentage share of individual types of forces of dynamic resistance shows different patterns with increasing frequency of vibrations:

3a) The power of inertia increases monotonically from 0 with increasing frequency $δ$ ,

3b) The power of dissipation increases until $δ =$ 1, which is the resonant frequency of the mechanical system, and reaches its maximum and then declines asymptotically to 0 as frequency tends to 0, $δ = \infty$ ,

3c) The power of elasticity decreases monotonically from its maximum at $δ \approx$ 0 to 0 as frequency tends to 0, $δ = \infty$ ,

3d) The powers of inertia and elasticity are equal at the resonant frequency, i.e. $δ =$ 1.

4) Energy efficiency of vibroisolation – defined as a ratio of total (input) power introduced into a mechanical system by the exciting force to the power of elasticity in the system – increases monotonically from 1 to 17.5, as frequency $δ$ changes from 0 to 5 and degree of damping $ξ =$ 0.1.

5) The power of elasticity is a good measure of the energy absorbed by elastic elements of the vibroisolation system and should be as low as possible.

6) Energy vibroisolation can be considered efficient when its value reaches or exceeds value 11.8.

Research in the domain of power distribution and energy flow in various systems of vibration reduction will be continued.

References

Crede C. E., Ruzicka J. E. Theory of vibration isolation. Shock and Vibration Handbook, Vol. 2, Chapter 30, McGRAW-HILL, New York, 1961.

Search CrossRef
Crede C. E. Application and design of isolators. Shok and Vibration Handbook, Vol. 2, Chapter 32, McGRAW-HILL, New York, 1961.

Search CrossRef
Harris C. M., Crede Ch. E. Shock and Vibration Handbook. Chapter 30-33, McGRAW-HILL, New York, 1976.

Search CrossRef
Goliński J. Vibroisolation of machines and devices. Ed. Scientific and Technical, Warszawa, 1979, (in Polish).

Search CrossRef
Crocker M. J. Handbook of Noise and Vibration Control, Part II: Fundamentals of Vibration. John Wiley & Sons, Haboken, New Jersey, 2007, p. 169-268.

Search CrossRef
Parszewski Z. Vibrations and Dynamics of Machines. WNT, Warszawa, 1982, (in Polish).

Search CrossRef
Dobry M. W. Optimisation of Energy Flow in Human – Tool – Base System (HTBS). Habilitation thesis, Series: Dissertations No. 330, Publishing House of Poznan University of Technology, Poznan 1998, (in Polish)

Search CrossRef
Dobry M. W. Foundations of Energy Diagnostics of Mechanical and Biomechanical Systems. Scientific Publishing House of the Technology Machine Operation Institute – National Research Institute, Poznan – Radom, 2012, (in Polish).

Search CrossRef

About this article

Received

Accepted

28 August 2014

Published

10 October 2014

Keywords

vibroisolation

power distribution in mechanical systems

energy efficiency

Acknowledgements

The investigations were made possible owning to partial funding by the Ministry of Science and Higher Education in research project: Energy-Information Issues of the Vibroacoustics, Diagnostics and Biomechanical Systems, No. 21/DSPB/3454.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.