An experimental study of the natural characteristics of the wheeled and the tracked self-propelled guns

1. Introduction

The natural characteristics of self-propelled guns have significant impact on its occupant comfort, guns vibration, as well as its dynamic strength, which have equal importance on its firing accuracy [1]. Therefore, it is of significant importance to study the dynamic characteristics of self-propelled guns, and to master the law of the dynamic characteristics and the impact on vibration. The low-order modes of self-propelled guns are mainly manifested in the rigid body motion, and elastic elements like tires or tracked rubber suspension feet, while the rigid body motion consists mainly of low-order modes like the pitch, translation and roll of the guns. Each modal and its corresponding natural frequency cast different effects on the vibration of self-propelled guns. There are relatively sharp contrast between wheeled self-propelled guns and tracked self-propelled guns due to their respective suspension systems and supporting means. Selecting two wheeled self-propelled guns of different caliber (called wheeled self-propelled gun A and wheeled self-propelled gun B) and two tracked self-propelled guns of the corresponding caliber (called tracked self-propelled gun A and tracked self-propelled gun B) as the research objects, the paper studies the dynamic characteristics of the guns using experimental modal analysis method. The study finds the low-order modes of the two types of guns and the differences between them.

2. The traditional experimental modal analysis method

The traditional experimental modal analysis method, gains modal parameters by testing excitation force and structural response, and by fitting the frequency response function or impulse response function [2].

Traditional experimental modal analysis system is comprised of the excitation system, response system and measurement system as well as analysis computing systems. During testing, the measured structure is given an excitation force $\left\{f\right(t\left)\right\}$ with a certain band width through the hammer or the exciter, and its vibration response $\left\{x\right(t\left)\right\}$ is also a signal consisting of system modal information. Through Fast Fourier Transform (FFT) on the force and response, Fourier spectrum $F\left(\omega \right)$ and $X\left(\omega \right)$ are obtained, and the frequency response function matrix is defined as:

Thus, the transfer function matrix of the structure can be obtained through the analytical processing of the excitation signal and response signal of each measuring point, and then modal parameters of the structure can be obtained.

3. The operational modal analysis method

Operational Modal Analysis Method [3-7] which identify the modal parameter through the response signal in working condition or environmental exciting Operating deflection shape (ODS) obtained through operational modal analysis method is the performance of a particular frequency in the working state or moment, the relative vibration between the two or more points on the structure, or the vibration state of a point with respect to all other points.

The basic idea of the operational modal analysis lies in the fact that there are similar expressions of the cross-correlation function and the impulse response function between two response points, modal parameter identification can be done in the time domain after the cross-correlation function between two response points has been obtained. When the excitation is unknown, operating deflection shape frequency response function (ODS FRF) is an ideal method for obtained the natural characteristics of the gun. ODS FRF is a frequency response function calculating response data in the working state, with response signal of some points as the reference signal, and other as flow response signal. By calculating the cross-spectrum between the flow response signal and the reference response signal, the ODS FRF substitutes the square root of the spectral amplitude of the flow response signal with the cross-spectral amplitude, and retains the phase information of response data between different measurement groups in cross spectrum. Therefore, ODS FRF is constituted by combining self-spectrum amplitude of the flow response signal and cross-spectrum phase information of the flow response signal as well as reference response signal, and its expression is:

where: $G_{xy}\left(\omega \right)=F_x\left(\omega \right)F_y^{*}\left(\omega \right)$ represents the cross-spectrum of the flow response signal and reference response signal; $G_{xx}\left(\omega \right)=F_x\left(\omega \right)F_x^{*}\left(\omega \right)$ represents the self-spectrum of the flow response signal.

If the excitation spectrum is relatively flat in the vicinity of natural modal, that is, it has characteristics similar to white noise excitation, the fitting method of the frequency response function can be used to fit ODS FRF curve, and thus modal parameters can be obtained. The frequency response function matrix contains the frequency response function curve, excitation Fourier spectrum and response Fourier spectrum. Frequency response function matrix elements can be expressed as:

where: $F_x\left(j\omega \right)$ represents Fourier spectrum of the response signal; $F_f\left(j\omega \right)$ represents Fourier spectrum of the excitation signal; $H_{x,f}\left(j\omega \right)$ represents transfer function of incentive and response signal.

If excitation in the vicinity of the natural modal meets the white noise excitation conditions, the amplitude of the Fourier spectrum can be substituted by a constant:

By Eq. (3) the relationship between the response and the frequency response function can be:

By the above analysis, it is evident that the information of the structure’s modal parameters is contained in the ODS FRF which has similar expression with frequency response function. Therefore, the frequency response function fitting method can be used in fitting the ODS FRF, and modal parameters can be obtained.

4. The experimental modal analysis of the wheeled and tracked self-propelled guns

With regard to the differences of natural characteristics of wheeled and tracked self-propelled guns, two different-caliber wheeled self-propelled guns and two tracked self-propelled guns with corresponding caliber are selected for testing the natural characteristics by using experimental modal analysis method, and studying the law of the low-order natural characteristics of those guns, and then analyze the differences of the low-order natural characteristics of those guns.

During the test, self-propelled guns are parked on a flat floor, analyzing the modes of the guns by using the traditional modal analysis method and operational modal analysis method. With the traditional modal analysis method, the top-deck corner of the chassis is to be selected as an excitation point for its large stiffness. With operational modal analysis method, engine of self-propelled guns is to be started to excite the guns, while the acceleration response of all the measuring points is to be recorded. For those guns, the acceleration responses in the same position are picked up, and been recorded and processed by the same dynamic signal analyzer.

In order to verify the feasibility of obtaining the natural characteristics of self-propelled guns through the operational modal analysis method, with wheeled self-propelled gun A as the test object, the natural characteristics of guns within 50 Hz frequency are tested by a contrastive test of traditional experimental modal analysis method and operational modal analysis method respectively.

Fig. 1 shows the measuring points of Gun A. Fig. 2 to Fig. 4 display the modal shapes of Gun A. Table 1 manifests low-order natural frequencies of the guns obtained by the two methods. The test results show that the results obtained by operational modal analysis method are consistent with those of traditional modal analysis method. For the first three vibration modes of the gun, the first mode is the pitching modes; the second mode is the up-and-down translation modes; the third mode is the roll mode.

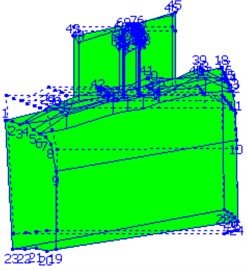
Fig. 1Layout of testing points for wheeled self-propelled gun A

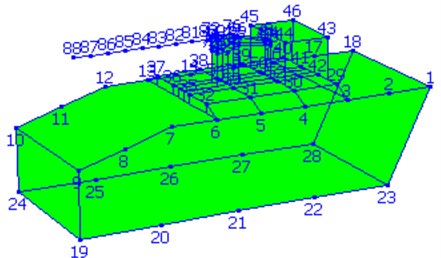
Fig. 2First-order mode of self-propelled gun A

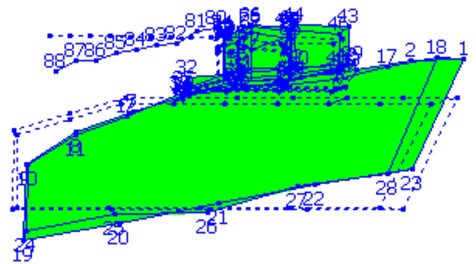
Fig. 3Second-order mode of self-propelled gun A

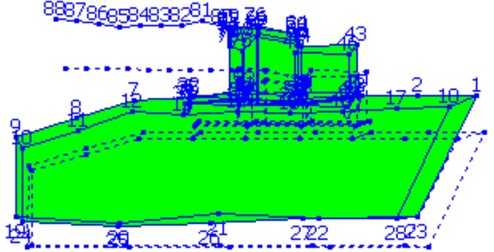
Fig. 4Third-order mode of wheeled self-propelled gun A

Similarly, through the operational modal analysis method, the modal parameters of self-propelled gun A and self-propelled gun B are obtained. Likewise, by using traditional modal analysis method, the modal parameters of tracked self-propelled gun A and wheeled self-propelled gun B have also been obtained, and the test results are shown in Table 2. Clearly, their low-order modal shapes are similar; when the modal shape are identical, the natural frequency of tracked self-propelled guns is greater than wheeled self-propelled guns.

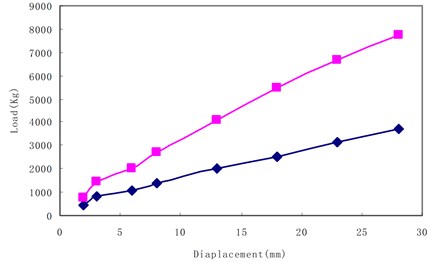
The experiment has tested the suspension equivalent stiffness of tracked self-propelled guns and wheeled self-propelled guns with same caliber, and the results show that the value of the chassis suspension equivalent stiffness of the tracked self-propelled guns is 1.7 to 2.1 times of that of the wheeled self-propelled guns. The test results are as Fig. 5 shows.

Fig. 5The chassis suspension equivalent stiffness test curve of two types of guns

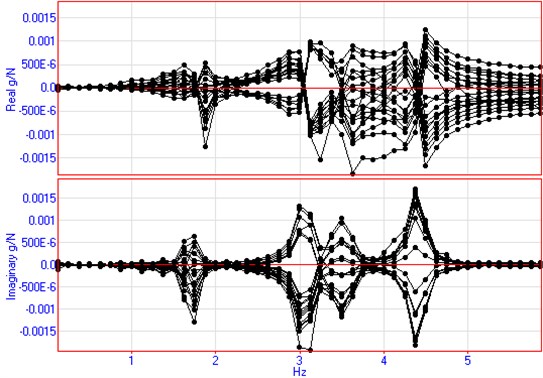
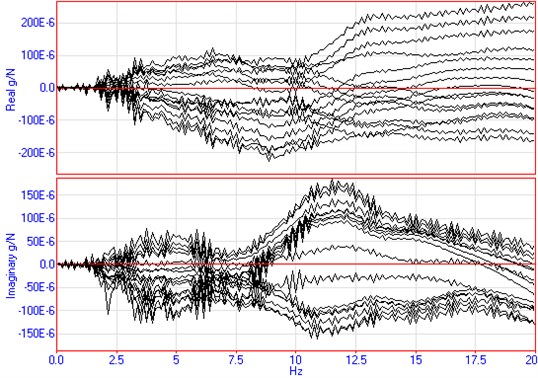
The frequency response curves of wheeled and tracked self-propelled guns are shown in Fig. 6 and Fig. 7 by using traditional modal analysis method. It is clear that when tracked self-propelled guns is tested by traditional modal analysis method, there will be low signal-to-noise ratio as well as a larger margin of modal parameter errors.

Fig. 6The frequency response curve of wheeled self-propelled guns using the hammering method

5. Test results analysis and conclusions

Traditional modal analysis method and operational modal analysis method are used to test the natural characteristics of wheeled and tracked self-propelled guns. Their modal parameters are obtained, and the following conclusions can be drawn:

1) Of the four selected self-propelled guns, their low-order modal shapes are reflected in such an order (in terms of frequency from low to high) as: pitch, up- and -down translation and roll.

Fig. 7The frequency response curve of tracked self-propelled guns using the hammering method

2) Of the four selected self-propelled guns, the corresponding natural frequencies of the gun’s pitch, up-and –down translation and roll modes in tracked self-propelled guns are greater than those of wheeled self-propelled guns respectively. The natural frequency of the wheeled guns is 1.7 to 2.1 times of the tracked guns. The chassis suspension equivalent stiffness of tracked self-propelled guns is greater than that of wheeled self-propelled guns, which accounts mainly for the higher low-order natural frequency of tracked self-propelled guns.

3) With regard to wheeled self-propelled guns, an accurate measure of the gun’s modal parameters is feasible by either the traditional experimental modal analysis method or the operational modal analysis method. When it comes to tracked self-propelled guns, the operational modal analysis method is more accurate.