Abstract
The object of this paper is the changing process of damping force as the falling weight impacting the elastomer buffer. The whole mechanical system is built up through practical test and simulation. According to the type of elastomer buffer and the experimental process in shock environment, velocity damping force identification model was established. Wavelet denoising and least square method were used for parameter identification of damping force. Considering the data saturation problem in the traditional least square method, the limited memory least square method was obtained to improve the identification method. The results of parameter identification of damping force based on limited memory method proved that the limited memory method was superior to least square method. The numerical results demonstrate the effectiveness of the identification model.
1. Introduction
Elastomer buffer has great application in various fields, which has the advantages of large capacity, stability, and simple structure. Over the years, the analysis and exploration of the damping process of elastomer buffer has been a hot research. For different application fields of elastomer buffer, accurate modeling of damping process is very meaningful to the study of mechanical system and noise reduction.
When the types of elastomer buffer and experimental environment are different, the damping parameter identification model is different. Accurate experimental subjects and establishing a right identification model directly determine the feasibility of damping parameter identification. The experimental object in this paper is a vertical impact process. According to the experiment, velocity-damping identification model was established. In the simulation phase, the wavelet denoising was used to filtering the experimental data. Aiming at the defects of the traditional least square method, the limited memory method was used to solve the problem of data saturation, which ensured that the algorithm has better precision of fitting.
2. Identification model
2.1. Elastomer buffer
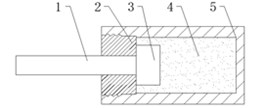
At present, the most widely used elastomer buffer for practical application is shown in Fig. 1. It is a single rod elastomer buffer. This kind of damper has a closed chamber, which is filled with viscoelastic fluid damping materials. When elastomer is impacted by external load, the buffer piston rod is pressed into the cavity. The damping material flows through the annular gap formed by piston and cylinder wall. The damping medium in cavity is compressed and the internal pressure increases, that caused the elastic force to the piston rod. At the same time, the piston head and damping structure produce great friction with the viscous damping medium. When the speed is higher, more viscous resistance will be produced. The impact kinetic energy can be turned into heat energy and elastic potential energy, which can be released in a very short time to achieve the effect of energy absorption. The elastomer also has good elasticity, that means, the volume will shrink under great external force. When the external pressure is up to 500 MPa, the compression ratio is not less than 17 % of the initial volume. When the external force is removed, the elastomers will automatic reset and release energy storage. And from Fig. 1, the numbers 1 to 5 represent piston rod, cylinder head, piston, resilient rubber and cylinder block.
Fig. 1Schematic diagram of elastomer buffer structure
2.2. Identification model
Energy buffer device can be manufactured according to different materials, energy dissipation mechanisms and structures. The experiment in this paper was performed in the shock environment. Speed-damping model is widely used for elastomer buffer in shock environment, which is shown as Eq. (1):
where is damping force, is damping coefficient, is the relative velocity of the piston and cylinder body and is velocity correlation coefficient (the larger its value, the smaller buffer’s nonlinear degree).
The model Eq. (1) shows is nonlinear. The complexity of nonlinear model is higher than that of linear model in the process of fitting. If it can be transformed into linear model, the fitting effect will be better. In order to linear fitting, logarithm was used on both sides of the formula which is shown as Eq. (2):
After the transformation above, the parameters need to be identified are linear parameters and . The data and can be obtained by the calculation of the damping force and velocity.
3. Identification algorithms
3.1. Least square method (LSM)
The least square method is a relatively mature algorithm. It has been widely used in scientific experiments and engineering technology. With the development and popularization of modern computer, LSM shows more powerful vitality. LSM is used for solving the problem of how to find reliable value from a set of measurements. Its basic principle is: a group of data (, , 1, 2,…, ) are obtained, and try to find a best fitting curve in which the difference quadratic sum of the value of each point on the curve and measured value is minimum.
In the design of experiments, in order to reduce the error, multiple point measurement is performed. The number of the equations is far more than that of undetermined parameters. These equations are called inconsistent equation group. The equations transformed by LSM are called the normal equations (here the number of equations is equal to the number of undetermined parameters). The undetermined parameters can be calculated by the normal equations.
3.2. Limited memory method (LMM)
The LSM is simple and practical, and its recursive algorithm is convergence and reliable. When the noise is white noise, the estimates can be unbiased, consistent and efficient. But with the growth of data, LSM will show the phenomenon of data saturation so that the recursive algorithm loses correction ability slowly. In that case, limited memory was introduced to LSM and the recursive algorithm called limited memory method was obtained. LMM can solve the problem of data saturation caused by LSM.
4. Study case
4.1. Experimental installation
Before the experiment, the buffer is arranged on the base. The impact hammer with quality of 30 kg was put in a suitable height. Then let the hammer fall free along the rail and impact the piston rod of buffer. The variation rule of displacement during the impact process was recorded by laser displacement sensor and data acquisition system. The actual installation of measuring equipment and buffer is shown in Fig. 2. And from Fig. 2, the numbers 1 to 5 represent impact hammer, acceleration sensor, laser displacement sensor, elastomer buffer and data acquisition equipment.
Fig. 2Schematic diagram of equipment

4.2. Data processing
During the falling process, displacement information of the hammer was collected by laser displacement sensor with sampling frequency of 10 KHz. After the displacement information was collected, acceleration information could be obtained by two differential operation of displacement. Combined with the quality of the hammer, the damping force time curve could be obtained. During the falling process, there would be noise and vibration interference.
Fig. 3Acceleration-time curve of low speed
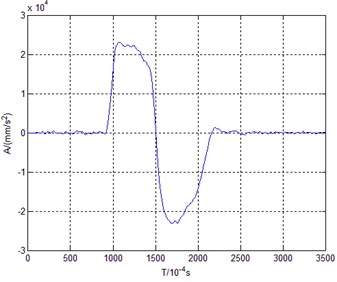
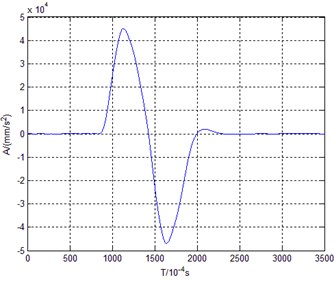
Fig. 4Acceleration-time curve of high speed
Therefore, the data need to filter so that the accuracy of data can be ensured. By adjusting the initial height of the hammer, displacement-time curves of different initial velocity can be obtained. Thus the damping force time curves of different initial velocity can also be gained. Two different initial heights, 300 mm and 700 mm were used to perform the low speed test and high speed test in this paper. The parameter identification of two sets of data was used to verify the validity of the identification model.
The acceleration-time diagrams of low speed and high speed are shown in Fig. 3 and Fig. 4.
Through the calculation, the damping force curves during the hammer impacting the buffer are shown in Fig. 5 and Fig. 6.
Fig. 5Damping force curve of low speed
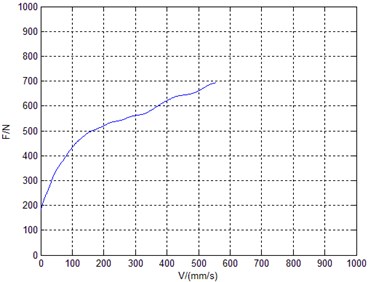
Fig. 6Damping force curve of high speed
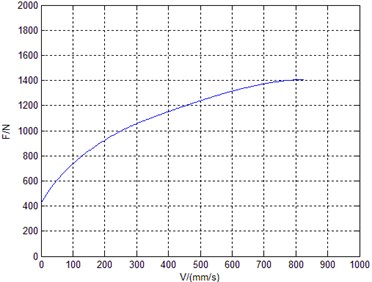
4.3. LSM for parameter identification
According to Eq. (2), parameter identification was performed with LSM respectively in low speed group and high speed group. The identification results were shown in Fig. 7, Fig. 8 and Table 1.
Fig. 7LSM result of low speed group
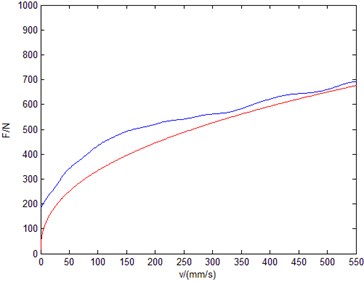
Fig. 8LSM result of high speed group
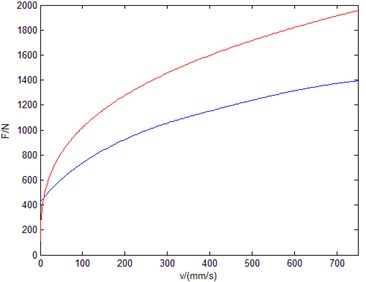
Table 1Identification result of LSM
Speed type | ∙(m/s)-1 | |
Low speed group | 263.34 | 0.4225 |
High speed group | 314.45 | 0.3965 |
Table 2Identification result of LMM
Speed type | ∙(m/s)-1 | |
Low speed group | 272.46 | 0.4352 |
High speed group | 282.56 | 0.4410 |
4.4. LMM for parameter identification
According to Eq. (2), parameter identification was performed with LMM respectively in low speed group and high speed group. The identification results were shown in Fig. 9, Fig. 10 and Table 2.
Fig. 9LMM result of low speed group
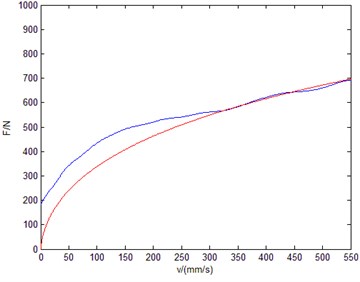
Fig. 10LMM result of high speed group
5. Conclusions
The damping force model of elastomer buffer in shock environment is nonlinear. Through linearizing the nonlinear equation, the original parameters will be obtained by inverse logarithmic operation. This method can guarantee the accuracy of the premise and greatly improve the efficiency of the algorithm. By identifying the model parameters with LSM and LMM, the correctness of the model is confirmed.
The traditional LSM has defects of data saturation. In the fitting process, the accurate parameter identification cannot be guaranteed with the growth of initial velocity. LMM can solve this problem and identification parameters can be also obtained accurately at high speed.
References
-
Dagen Wong, Zhuhun Lu, Bin Xu Experimental study on mechanical properties of viscous damper. World Earthquake Engineering, Vol. 18, Issue 4, 2002, p. 30-34, (in Chinese).
-
Guangqiang Zhou, Lina Yang, Aijun Yang, Zhongzhang Sun Research progress on characteristics of elastomer buffer. Silicone Material, Vol. 25, Issue 1, 2011, p. 40-43, (in Chinese).
-
Xianjun Shi, Jian Liao, Changli Ma, Rong Zhang GLS Parameter identification and simulation based on Matlab. Computer and Digital Engineering, Vol. 37, Issue 8, 2009, p. 173-175, (in Chinese).
-
Gancheng Wang, Sujuan Jiao, Jinya Sun, Hongguang Li Shock experiments research and modeling analysis of elastomer dampei. Noise and Vibration Control, Vol. 6, 2010, p. 55-62.
-
Wenyu Li, Hong Du, Yanbin Liu Application of least square method based on limited memory in parameter identification. Natural Sciences Journal of Habbin Normal University, Vol. 23, Issue 4, 2007, p. 23-25, (in Chinese).
-
Cong Liu, Xiuxian Sun, Haijun Li An identification method combing forget factor with limited memory method. Electronics Optics and Control, Vol. 13, Issue 1, 2006, p. 48-66, (in Chinese).
-
Park S. W. Analytical modeling of viscoelastic dampers for structural and vibration control. International Journal of Solids and structures, Vol. 38, 2001, p. 8065-8092.
-
Jia J. H., Shen X. Y., Hua H. X. Viscoelastic behavior analysis and application of fractional derivative Maxwell model. Journal of Vibration and Control, Vol. 13, 2007, p. 385-401.
-
Terenzi G. Dynamics of SDOF systems with nonlinear viscous damping. Journal of Engineering Mechanics, Vol. 125, Issue 8, 1999, p. 956-963.
-
Gusella V., Terenzi G. Fluid viscous device modeling by fractional derivatives. Structural Engineering and Mechanics, Vol. 5, Issue 2, 1997, p. 177-191.
-
Tsai C. S. Temperature effect of viscoelastic dampers during earthquake. Journal of Structural Engineering, Vol. 120, Issue 2, 1994, p. 394-409.
-
Pekcan G., Mander J. B., Chert S. S. The seismic response of a 1:3 scale model R.C. structure with elastomeric spring dampers. Earthquake Spectra, Vol. 1, Issue 2, 1995, p. 249-267.
-
Lee D., Taylor D. P. Viscous damper development and future trends. The Structural Design of Tall Buildings, Vol. 10, 2001, p. 311-320.
