Increase of productivity in brittle material processing by the application of intermediate elastic elements in tool structure

1. Introduction

Traditionally the principal scheme of brittle materials ultrasonic treatment is based on the application rigid structure tools with concentrators of longitudinal oscillations. Research of material treatment productivity with the application of ultrasonic tools of such rigid structure is based on the analysis of the influence of certain acoustic and technological factors. Frequency, amplitude and type of oscillations can be considered as acoustic parameters while – materials of the blank and the tool, the speed of relative motion, static pressure force of the tool to the treated part, type and dimensions of abrasive grains, concentration of the grains in suspension, treatment depth and conditions for abrasive flow as technological parameters. Majority of these factors are strongly interrelated.

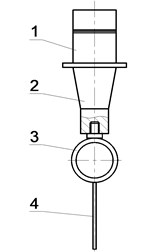
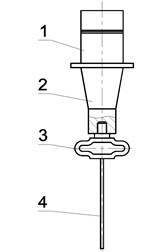
But the impact of the structure of ultrasonic system which serves as the tool is not deeply investigated up to now. In the present research the concept of elastic element introduction into the tool structure is presented (Fig. 1). In consists of piezoceramic transducer 1, conical concentrator 2, intermediate elastic loop shaped concentrator in the form of a circular ring or a loop with parallel sides 3 and rod shaped tip of the instrument 4. The elastic elements serve as the members ensuring the amplitude increase of the tool’s tip as well as the member allowing generating oscillations mode the most efficient for technological purposes. Thus performance characteristics of the developed tools significantly exceed characteristics of traditional rigid structure tools. One of the advantages of these elastic concentrators is the achieved possibility to obtain vibration-shock regime followed by low frequency component in the instrument oscillations spectrum what strengthens ultrasound effect on technological process duration.

Fig. 1Schematics of acoustic tools with elastic concentrators: 1 – piezoceramic transducer, 2 – conical concentrator, 3 – intermediate elastic loop shaped concentrator in the form of a circular ring or a loop with parallel sides; 4 – rod shaped tip of the instrument

a)

b)

2. Theoretical assumptions

The number of researches of world class authors on theoretical calculation of natural frequencies of elastic elements is not so great. Together there is no extensive data on the experimental researches of oscillatory processes in elastic elements working in different frequency ranges of forced oscillations. Therefore the research results on the properties of elastic elements working in the range of ultrasonic frequencies are of particular importance. Technological ultrasonic devices for processing of holes represent vibrating systems, which consist of transducer of electrical oscillations and transformer of the oscillations to which the working tool is attached. Analysis of such vibratory system indicates that one of the promising ways of these systems modernization is the application of elastic elements – the resonators functioning as energy accumulators. Elastic elements of oval or round shaped ring, spring type coiled along axis or transversally to it, bellows, membranes and other can be used as such kind of the resonators.

Conventional schemes of ultrasonic oscillatory systems consist of stiff elements; nevertheless the systems including elastic bodies might be of high interest. They could serve as accumulators of motion and perform the function of kinematical transfer and transformation of motion. Nevertheless this item is not investigated sufficiently; therefore practical recommendations for the selection of elastic elements for technological ultrasonic systems do not exist. It is obvious that for such purpose theoretical background of the calculation of elastic bodies is necessary. The condition of obtaining resonance in an acoustic system with elastic bodies could be considered matching of natural (eigen) frequencies of these bodies and the frequencies of forced oscillations excited by the transducer of ultrasonic oscillations. Calculation schemes of oscillatory processes in elastic bodies include the evaluation of longitudinal, transversal, flexural and torsional oscillations.

In a number of cases resonance frequency of typical elements can be theoretically calculated, e.g. for spring type element the resonance frequency equals [1]:

where $d$, $n$, $D$ – diameter in cross section, number of windings and diameter of the wire accordingly.

Resonance frequency of the ring element [2]:

where $\sqrt{Eg/\mathrm{\gamma }=c}$ – sound speed, in steel equal to – 5050 m/s; $r$ – radius of the ring, $i$ – number of waves along circumference.

The formulas above illustrate that natural frequency of an elastic tool can be found by preliminary determination of its geometrical parameters. As the input data for the calculation, the given frequency of ultrasonic oscillations and diameter of the wire can be used. Each of the given designs of tools has its own characteristic features which are predefined by design parameters and dimensions of its elements. The common requirement for all the presented schemes is the elimination of abrupt shape distortions which function as oscillation dampers.

Elastic bodies are mechanism links which can deform significantly under the action of external forces. As such elastic bodies – rings, planar ovals, ellipses, springs, bellows, membranes and other shape bodies can be used. The most widely spread shapes from the mentioned ones are elastic rings, helical and planar springs, of planar oval and elliptic form elastic elements (i.e. Burdon’s springs), coiled tubular springs with different cross-sectional parameters, elastic bellow type bodies and elastic supports.

Natural frequencies of closed circular rings can be determined using the equation [3]:

where number $k=$1, 2, 3, … characterizes the number of oscillation nods in the ring.

Oscillations of springs are studied the most deeply. Longitudinal oscillations of coil springs with a free end are calculated by the formula [7]:

For other types of elastic bodies it is possible to use the data provided in reference [3-7].

Currently the topic of natural frequencies calculation of closed rings is already deeply studied and this indicates adequately that particular characteristics depend in many aspects on geometrical parameters of elastic bodies. Calculation and selection of such parameters ensuring natural frequency matching to the frequencies of forced oscillations, enables obtaining resonance of the ultrasonic system suitable for industrial application in technological systems.

Fig. 2The shapes of elastic elements

a)

b)

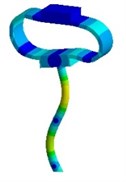
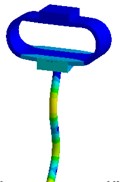
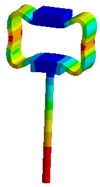
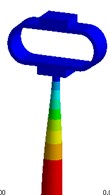
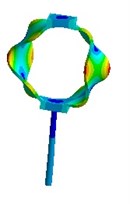
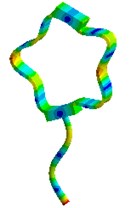
Nevertheless visual evaluation of the wave processes which are excited in a structure with elastic elements under the effect of forced oscillations of different frequencies are not provided by mathematical model solutions of the systems. The task becomes more complicated in case of the variation of the parameters of elastic elements. Therefore, in the present research an attempt to carry out the visual analysis of wave processes in ultrasonic technological systems with elastic elements was made. This problem was solved with the use of the simulation software package “ANSYS”. Analysis of the most typical elements (Fig. 2 – oval and round spring), was performed in the research. The frequency diapason of the forced oscillations in the range of ultrasonic oscillations (from 18 to 43 kHz) was investigated. The obtained results are presented in Fig. 3.

Analysis of the obtained images of elastic elements confirms that, at the same their initial parameters, the change of frequency of forced oscillations leads to the change of oscillation mode and wave number. The colour scale (from the blue representing min to the red representing max) indicates the values of displacement fields in different sectors of elastic elements. It can be observed that different types of deformations are generated in the working element – the tip of the oscillatory system.

Fig. 3Modal shapes of oscillatory system with elastic elements

a)

b)

c)

d)

e)

f)

g)

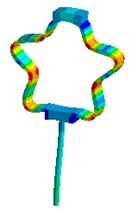
h)

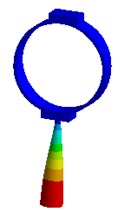
i)

3. Experimental results

For experimental analysis four types of elastic concentrators were manufactured as presented in Fig. 4. Two types of them are circular shaped – with constant and variable cross sections and the other two are of closed loop shape with two parallel sides with constant and variable cross sections as well. All the concentrators were made of steel 45 as this material satisfies the necessary requirements: it has sufficient elasticity characteristics, ensures the possibility to transfer mechanical oscillations in ultrasonic range, has sufficient strength, and ensures reliability, good technological properties of the system.

Fig. 4The shapes of elastic concentrators

a)

b)

c)

d)

The obtained results showed that introduction of an elastic element into the structure of ultrasonic tool allowed to increase oscillation amplitude of the tool’s tip up to 3.5 times.

In order to make analysis of the productivity experimental comparative studies when drilling brittle material were performed. To represent the brittle material specimens from the glass (М7 GОСТ111-2001) of the thickness 8±0.1 and the hardness of 6 on Mohs scale were used. The obtained results reveal that in case of the application of circular shape concentrator with constant cross section the productivity increase on average 1-2 times and in case of the application of concentrators with variable cross sections (both circular shaped or close loop shaped with parallel sides) it increased 2-4 times.

4. Conclusions

The use of elastic elements as an intermediate element in technological systems opens new opportunities for controlling the material processing processes by changing the frequency range of the working oscillations and geometrical parameters of elastic elements.

The experimental research results allows concluding that the maximum productivity in processing brittle materials can be achieved by applying intermediate elastic concentrators with variable cross sections as they allow both to increase oscillation amplitudes of ultrasonic range and to accumulate energy.