Revisiting the models of vibration screening process

1. Introduction

Vibration screening is a process of great significance for granular materials processing. Notwithstanding the fact that the process has been studied with careful attention [1-4], its theory is by no means complete yet. Particularly, the relative role of stochastic and deterministic processes has not been clarified so far.

The purpose of this paper is to fill this gap partially. It covers two fundamentally different vibratory screening models. The first, analytical model enables establishing the relative impact on the screening rate of the deterministic factor of segregation and probabilistic factor of diffusion, as well as of a number of equipment parameters. The second model allows taking into account the effects of particle shapes in the material.

2. Continuous model of vibratory screening with account of diffusion and segregation

The study covers the vibratory screening process occurring in a horizontal rectangular tray with a bottom screen, allowing penetration of particles of appropriate size through its openings (Fig. 1). The granular medium in consideration consists of two fractions: undersize (fine fractions penetrating through the screen openings) and oversize particles (coarse fractions remaining in the tray). When under vibration, the granular medium is displaced along the tray at constant speed $w$.

It is assumed that particle concentration in the undersize, within the one-dimensional model under consideration, in a certain volume of $bh∆z$, depends only on coordinate $y$ and time $t$, $c=c(y,t)$. Assuming that for longitudinal coordinate $z$ this dependence is represented by the function of $c=c(y,z/w)$, the following function is of interest:

which describes the changes in average concentration along the tray, i.e. the screening intensity.

Our goal is to study the dependence of $C\left(t\right)=C(z/w)$ on the random and predetermined factors of dispersion and segregation. Under the assumptions made in the simplified model proposed in [1-3], the screening process is described by partial differential equation:

at boundary conditions of:

at initial condition of:

$V>0$ describes the segregation rate, i.e. the advance rate of fine particles towards the bottom of the vessel. The first condition (2) corresponds to the assumption that the flow of undersize particles through the screen openings is proportional to the concentration of these particles near the screen. The second condition implies the absence of inflow of particles via the layer surface and the initial condition (3) implies original uniform distribution of undersize particles throughout the layer. When looking for a solution for Eq. (1) according to the Fourier method (see, for example, [5]) we can obtain the condition for the existence of non-trivial solutions:

where:

The locations of roots $r_n$ of the transcendental Eq. (4) is shown in Fig. 2; the roots correspond to the intersection points of curves $y=\cot r$ and $y=r/p_h-f/r$.

Fig. 1The layer of the material under consideration

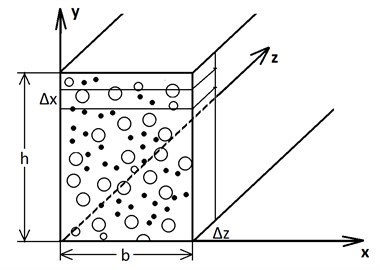
Fig. 2The roots rn of the transcendental Eq. (4)

It may be seen that each interval $(0,\pi )$, $(\pi ,2\pi )$, ... contains one equation root, and at sufficiently large values of $n$ they contain roots $r_n=\pi n$.

If, at a first approximation, we consider only the first members of the series obtained by the Fourier method, which “set the pace” of the process, taking into account initial condition (3), the following is true:

It should be noted that the approximation formula is consistent with the empirical formulas of the elementary screening theory, according to which the concentration of undersize particles decreases exponentially with time and coordinate $z=wt$. Naturally, in experimental theory, the exponent is a purely empirical value, and its dependence on the parameters is not taken into account.

3. Monolayer model

Various external factors and characteristics of granular materials are a subject of thorough investigations as potential effectors of the screening dynamics [6-8]. Though the factor of material particles shape is believed to be of importance [8], the existing approaches can hardly satisfy the academic community in terms of reliable and consistent explanation of the nature of the shape factor effect. The basic model for the study presented in this report assumes that material particles are transported along the screening surface and may pass through the screen into the through product at each toss caused by surface oscillations. The probability of single particle passing through a screen opening was initially determined using the Gaudin formula recorded for the spherical shape of particles, while the clear area of the screen was recalculated with account of its hole shielding by the material flow. If the material is seen as a granulation of $N$ size grades $D_i$ ($i=\text{1,…,}N$), with specified concentration in the initial product $C_i$, the expected recovery to through product may be calculated for each of these grades for a screen with square holes and side length $d_0$ as follows:

where $S$ – shielding factor (an experiment showed that for sufficiently dense monolayer material flows this may be considered equal to oversize concentration $S~\sum _{D_i<d_0}{C}_i$, $\phi$ – clear area, $P_i$ – penetration probability determined using the Gaudin formula ($P_i={\left(1-d_i/d_0\right)}^2$), $N_p$ – maximum expected number of particle presentations on the screening surface. The maximum number of presentations depends on screen vibration parameters and the particle exposure time determined, in turn, by the vibration displacement rate, and hence by friction and elasticity characteristics of material particles [9]:

where $\omega /2\pi$ – screen vibration frequency, $v$ – vibration displacement rate, and $l$ – screen length.

Three materials were selected for experimental tests: complex polymetallic ore from Kondyor deposit, copper-nickel ore from Pechenga deposit and granitic rock from Semiozersk deposit. Below is a table of grain-size distribution of these materials and their basic mechanical parameters.

Fig. 3 shows calculation results for material particles recovery to the through product, using the previously described method. Analytical recovery curves are provided with bold dots indicating averaged experimental data for a series of screening operations.

It may be seen that the copper-nickel ores had relatively smaller shielding coefficient than polymetal ore, which naturally preconditioned better extraction. However, it should be noted that the experimental data showed consistently lower recovery rates than were expected. Below is a comparative analysis of these two materials.

Fig. 3Theoretical extraction curves and experimental points for: a) granite, b) polymetal ore, c) copper-nickel ore

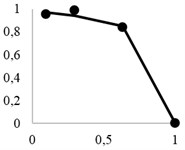
a)

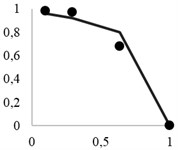
b)

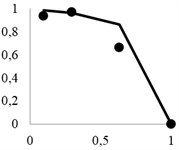
c)

A detailed study using image analysis methods demonstrated that the deviation of experimental points from theoretical curves may be due to the differences in particle shapes. This suggested that particles of copper-nickel ore are somewhat more elongated than other samples. Fig. 4 shows photographs of particles of materials studied. Table 2 presents the respective data on average aspect ratios of the smallest parallelepipeds these particles could be inscribed into.

As a result, it was suggested to recalculate the penetration probability for single particles approximated by ellipsoids using the specified semi-axes ratio. Assuming that particle orientation at the time of the fall is determined by Euler angles $(\phi ,\psi ,\vartheta )$ and its semi-axes have sizes of $a$, $b$ and $c$, its projections on the sides of a square screen hole may be calculated as follows (see Fig. 5):

A similar method may be used to calculate $d_B$ projections.

Fig. 4Particles of the materials under consideration: a) polymetal, b) copper-nickel

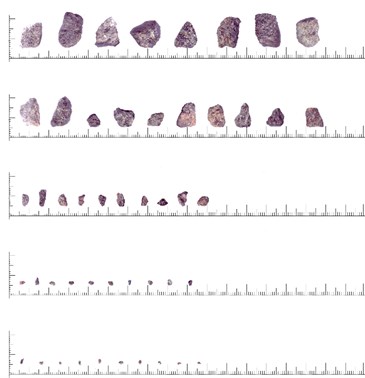
a)

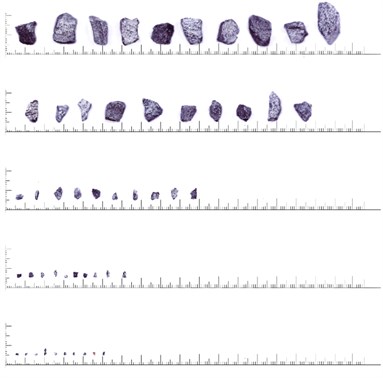
b)

Fig. 5Particle projection

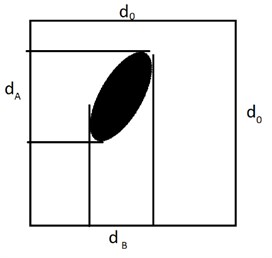
In this case, using the same logic applied when deriving the Gaudin formula, the penetration probability for a particle in such a position may be recorded and averaged over all rotations as follows:

The resulting formula may be easily generalized for rectangular and slot openings in the screening surface.

The recovery curves, as updated using the new probability formula, are shown in Fig. 6. Dashed lines indicate the new theoretical data.

Fig. 6Updated extraction curves

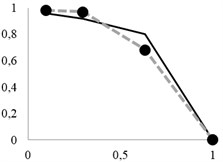
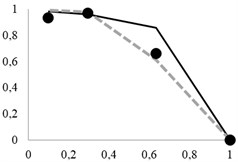
As can be seen, the resulting probability formulas for single particle penetration through a screen opening significantly increase the accuracy of data obtained.

4. Conclusions

Analysis of expression (5) allows making the following conclusions:

– The screening process may be quite intensive even in the absence of segregation (see also [3]).

– At the same time, the rate (intensity) of the process increases in the presence of the segregation effect that is accounted for using member $V\frac{\partial c}{\partial y}$.

– As one would expect, at a relatively high diffusion coefficient $D$, the screening rate depends on diffusion processes, while segregation plays a minor role. In contrast, at a relatively low diffusion coefficient $D$ or relatively high values of $\nu$, the segregation processes prevail.

The analytical model under consideration allows analyzing the relationship between probabilistic and deterministic factors in the screening process. However, the study does not cover a number of important aspects of the process, in particular, the dependence of $D$ and $\nu$ on vibration parameters.

It was established also that consideration of particle shapes might play an important role in vibration screening simulations. The improved probability equation for individual particle penetration into the through product may be used to increase the accuracy of calculations made via traditional methods, or particularly in conjunction with the presented original screening mathematical model for thin material layers. The above computational models may also be used for optimization of process and design parameters of vibrating screens in order to separate materials by specified parameters [10].