DEM simulation and experimental study on the screening process of elliptical vibration mechanical systems

1. Introduction

In order to build a resource-saving and environment-friendly society, the development mode and production mode of machinery industry must take into full consideration the coordinated development of economic benefits, environmental benefits and social benefits. We should attach importance to the research and the application of green and efficient technology so as to promote sustainable development of machinery industry. Vibration machinery that we focus on in this paper is a screening machine widely used in mining, metallurgy, chemical industry, food and other industries. The performance of vibrating screen directly affects the production efficiency and screening quality and has an important impact on enhancing the utilization rate of raw materials. The screening process is very complicated, and it is subject to vibration parameters, technics parameters, materials properties and many other factors [1]. As for the research on vibration screening process, the methods adopted by traditional research rely mainly upon screening experiments and personal experience. Moreover, it takes a very long time to finish the whole research. The research costs are so high that it is hard to achieve a deeper study of the screening process. Discrete element method (DEM) is used as a numerical method to calculate the mechanical behavior of particle systems which can accurately reflect the mechanism of the screening process and demonstrate the movement of materials on the screen surface and the behavior of the sieve. [2]. Therefore, discrete element method (DEM) has become an important and effective method to study the screening process [3, 4]. At present, research on vibration screening process mainly focuses on linear vibration and circular vibration, and there are relatively few studies on the elliptical vibration screening process. Elliptical vibration combines the advantages of circular vibration and linear vibration. Materials on the screen surface can attain a higher conveying speed and elliptical vibration has better loose effects on materials layer, which can ensure high yield and screening quality simultaneously [5].

Based on the above facts, the discrete element method is used to analyze the elliptical vibration screening process, and the test bed of vibrating screen for sieving materials is particularly established to carry out a typical materials sieving experiment for the same simulation system and study the screening process of elliptical vibration machinery. EDEM is the world's first universal CAE software designed to simulate and analyze particle processing and particle production operations by using discrete element method. The core idea of EDEM is discrete element method (DEM). By combining the advantages of the EDEM simulation and experiments, coupled with the comprehensive comparison of the results of simulation research and experimental research, we have analyzed the law of influence of vibration parameters on the materials’ conveying speed and sieving efficiency during the elliptical vibration screening process. Hence, we can expound the screening process of elliptical vibration machinery better and provide data support based on experiments and simulations at the same time. The screening model of the elliptical vibration machinery is built in Sections 2, and the test bed of screening experiment is set in Section 3. Section 4 deals with DEM and presents the experiments to verify the accuracy of the modeling and the simulation. At last, conclusions are drawn.

2. The materials screening model of the elliptical vibration machinery

The discrete element method is a numerical method to study the physical structure and law of motion of discrete particulate. Different from the description of particles in the continuum theory which is based on Elastic-Plastic Mechanics, the discrete element method is not based on the principle of minimum potential energy but rather the Newton’s second law of motion. The discrete element method takes the contact theory of spherical particles presented by Hertz and Mindlin-Deresiewicz as a basis so as to realize numerical computation about particle movement and various micro behaviors by using the simplified contact model of soft or hard sphere particles. Here is the brief introduction to the Hertz Contact Theory and the Mindlin-Deresiewicz Contact Theory [6].

(1) Hertz contact theory.

The Hertz Contact Theory assumes that the material is homogeneous, isotropic, and fully elastic; the friction of the contact surface is negligible, and the surface is the ideal smooth surface. Under the above assumption, the Hertz Contact Theory can be established.

As shown in Fig. 1, when two spherical particles having a radius of $R_1$ and $R_2$ are in contact, the normal contact force $F_n$ corresponding to the amount of overlap $\alpha$ in the normal direction can be calculated by the Hertz contact theory:

where $R^{\mathrm{*}}$ and $E^{\mathrm{*}}$ are the equivalent radius and equivalent Young’s modulus respectively, which are calculated by the following formula:

where $E_1$ and $E_2$ represent the Young’s modulus of spherical particles with radius $R_1$ and radius $R_2$ respectively; ${\mu }_1$ and ${\mu }_2$ represent the Poisson’s ratio of spherical particles with radius $R_1$ and radius $R_2$ respectively.

As seen in the Eq. (1) that in a time step, if the increment of the overlap between the two contact particles is $∆\alpha$, the corresponding normal contact force increment $∆F_n$ is:

where the contact radius $a=\sqrt{\alpha R^{\mathrm{*}}}$.

Fig. 1Schematic diagram of contact between two particles

(2) Mindlin-Deresiewicz contact theory.

The tangential force increment $∆T$ of the contact surface corresponding to the tangential displacement increment $∆\delta$ of the contact surface is:

where $k=$ 0, 1, 2 correspond to the case of loading, unloading and reloading respectively.

If $\left|∆T\right|$ < $\mu ∆F_n$ then ${\theta }_k=$ 1, if $\left|∆T\right|$ ≥ $\mu ∆F_n$ then:

where $\mu$ is the surface friction coefficient between particles and $F_n$ is the normal contact force, and $G^{*}$ is the equivalent shear modulus:

where $G_1$ and $G_2$ represent the shear modulus of spherical particles with radius $R_1$ and radius $R_2$ respectively and $T_k$ is the tangential contact force considering the case of unloading or reloading, which is updated at each time step:

In this paper, a simulation model is established according to the method used in the research of Dong K. J and Yu A. B [7] and we have carried out the following four tasks: (1) A three-dimensional simplified model with the same scale as the test bed is established so as to compare the simulation results and the screening experiment results; (2) The size of aperture of the steel perforated sieve plate is the same as that used in the experiment; (3) The trajectory of screen surface is elliptical; (4) The size and properties of materials are the same with the experiment. The DEM model is as shown in Fig. 2.

Fig. 2Vibrating screen simulation model

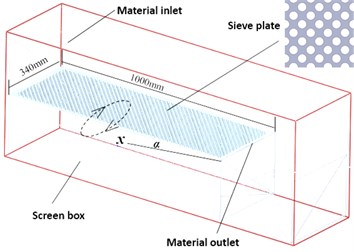
In order to ensure that the research results can provide an effective theoretical basis for actual production, this paper will guarantee the reliability of the model from the following aspects: (1) EDEM algorithm as well as its reliability used to calculate motion and collision of discrete particle system have been verified by many scholars. (2) The scholars have verified the reliability of the EDEM simulation model by experiments. (3) The adoption of model in this paper is based on the research results of Dong and Yu as well as the real parameters from Jahani M. [8]. The simulation parameters used in this paper are shown in Table 1.

The simulation model adopts the Hertz-Mindlin Soft-Sphere dry contact to simulate the materials collision process [9, 10]. The reliability of this collision model has been verified by many researchers and applied to the vibration screening simulation.

Fig. 3Simulation on the screening process

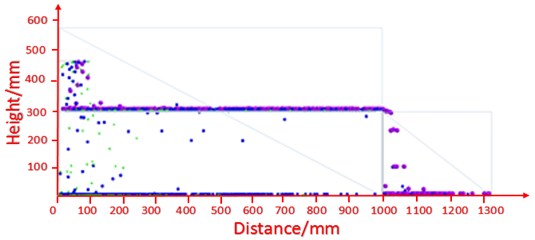
As shown in Fig. 3 for the screening simulation process, the particle factory produces particles with different size at a constant speed. The purple particles in the screening experiment cannot be sieved. The blue particles are corresponding to particles which are difficult to be sieved. And the green particles correspond to the particles which are easy to be sieved [11]. The materials waiting for screening fall to the screen surface by gravity, and then pile up the materials layer. And the materials are layered under the force of the motion of the screen, the particles which are difficult to be sieved continuously moves to the outlet. Finally, the number of particles at the inlet and outlet as well as the sieving quantity will achieve dynamic equilibrium [12]. Since the actual production focuses on the dynamic equilibrium, the simulation data in this paper are all collected from the dynamic equilibrium state of the materials on the screen.

3. Construction of sieving experimental test bed

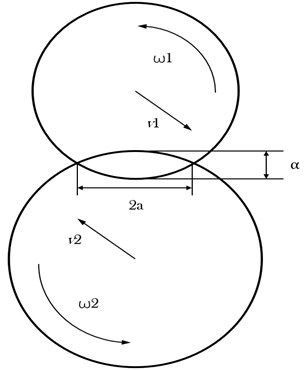
This paper has pursued a research on the elliptical vibration screening process. According to the principle of self-synchronization, the elliptical test bed of self-synchronization driven by dual machines with unequal mass and diameter product was built, as shown in Fig. 4. The test bed chose two three-phase asynchronous 4-stage vibration motors whose excitation force ratio is 2:1 and the two vibration motors are installed at 45° in the screen body.

Fig. 4Elliptical sieve vibration experiment system

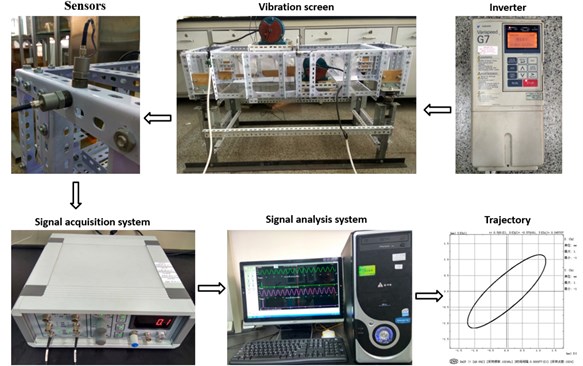
According to the force center theory [9], we can adjust the position of the two vibration motors in order to make the center of force coincides approximately with the center of mass of the screen body. The rotation speed of the two vibration motors is controlled by a converter. The vibration detection system consists of a signal acquisition instrument and sensors which measure the vertical and horizontal vibration of the screen body respectively. Acceleration sensors will measure the acceleration value and then obtain the corresponding displacement value by quadratic integral. The horizontal and vertical vibration signals are respectively used as the $X$-axis and $Y$-axis in the plane coordinate system to synthesize the trajectory of test bed [13].

After the experiment, the elliptical vibration test bed can achieve stable elliptical trajectory which is as shown in Fig. 4. The natural frequency of the elliptical vibrating screen is 3.8 Hz. When the vibration frequency exceeds 10 Hz and the experimental platform works in the resonance region, the test bed can meet the requirements of subsequent experiments.

As shown in Fig. 5, the sieve experiment adopts the circular steel perforated sieve plate whose diameter is 10.00 mm, and the parameters of the sieve plate are the same as the simulation parameters.

Fig. 5Sieve plate

The sieve experiment selects three kinds of spherical particles made of PC plastic with different sizes as screening objects. As shown in Fig. 6, the diameters of the three particles are 13.70 mm, 9.70 mm and 5.80 mm respectively. They respectively represent the obstructed particles (purple, pink particles), the particles difficult to be sieved (white, blue particles) and the particles easy to be sieved (green, yellow particles). Finally, the three types of particles are mixed at the same mass ratio.

On the basis of the elliptical test bed of self-synchronization driven by dual machines, the sieve plate is installed at the bottom and the collection box of obstructed particles is placed at the outlet. The collection box of easy-to-be-sieved particles is placed under the sieve plate. A screening experimental set-up is as shown in Fig. 7.

Fig. 6Screening experiment materials

Fig. 7Screening experiment equipment

This biaxial elliptical vibrating test bed has the functions of adjusting screen surface inclination, vibration frequency, amplitude and vibration angle, etc. The adjustment of vibration angle is realized by the frequency conversion technology, and Fig. 8 is the schematic diagram of adjustment of vibration angle.

Fig. 8The adjustment of vibration angle

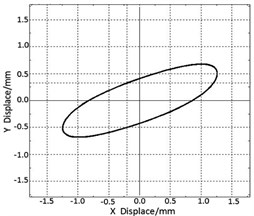
a) 24°

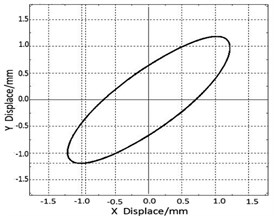
b) 45°

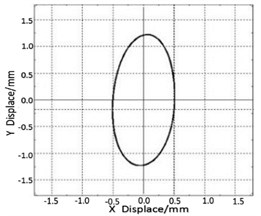
c) 88°

Fig. 9 shows the states of materials before and after the screening experiment. Fig. 9(a) represents the mixed materials of three different sizes but equal mass before sieving, Fig. 9(b) represents the materials in the outlet, and Fig. 9(c) represents the screened materials. The screening process and the results show that: Most of the easy-to-be-sieved particles are quickly separated during the screening process and gradually decrease from inlet to outlet. The difficult-to-be-sieved particles are continuously separated along the direction of conveying materials. At the end of the screen plate, the easy-to-be-sieved particles are basically separated through sieving so the contact opportunities between the difficult-to-be-sieved particles and the screen plate increased and the probability of sieving at the end of the screen plate increased correspondingly.

During the sieving experiment, in order to reduce the experimental error, we repeated the experiment for five times and take the average of the experimental results for the same group of screening experiments.

Fig. 9The materials’ state before and after the screening experiment

a) The materials from inlet

b) The materials from outlet

c) The materials after sieving

4. Analysis of DEM simulation and screening experiment

In order to study the law of particle movement and sieving under the mode of elliptical vibration trajectory, we have carried out the screening experiment and DEM simulation [14, 15] to study the influence of screen surface inclination, vibration angle, vibration frequency and amplitude on the conveying speed and sieving efficiency of materials during the screening process.

4.1. The evaluation index on screening quality

(1) Sieving efficiency.

The particles used in the experiment and simulation in this paper are spherical. For spherical particles, the particles which are larger than the size of the screen aperture will not pass through it. Hence, the equation applied for calculating screening efficient is as follows:

9

$\eta =\frac{m_{Sp}}{m_{St}}\times 100\mathrm{}\mathrm{\%},$

where $m_{Sp}$ represents the total mass of the sieved particles in the collection box under the sieve plate whose size are smaller than the screen aperture and $m_{St}$ represents the total mass of particles in the inlet whose size are smaller than the screen aperture.

(2) Conveying speed of the materials.

For the simulation model, this paper adopts the data analysis module of EDEM to count the forward conveying speed of particles which are on the screen in the horizontal direction. By extracting the average speed of the particles on different stages of the screen, we can obtain the average value of the conveying speed of particles, as shown in Fig. 10.

Fig. 10Statistics results of the conveying speed of materials in simulation model

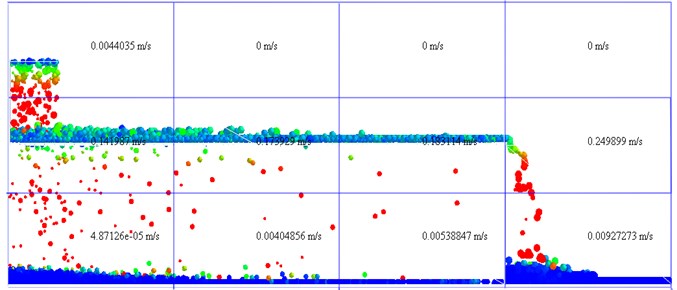
During the process of screening experiment, it is impossible to adopt the method of simulation analysis to calculate the conveying speed of materials. Therefore, the method to extract the conveying speed of materials during the experiment is as follows: As shown in Fig. 10, 40 pink particles with the same diameters as the purple particles are used to act as the obstructed particles. During the screening process, the pink particles are poured into the materials inlet. We use a stopwatch to record the time of every particle moving from the materials inlet to the materials outlet. The screening experiment is repeated five times in each group to obtain the average time of the pink particles. According to Eq. (10), the conveying speed of materials is calculated during the screening process:

10

$v=\frac{L}{\overline{t}},$

where $L$ represents the length of sieve plate and $\overline{t}$ represents the average time of the pink particles moving from materials inlet to materials outlet.

4.2. The screening process experiment and simulation results

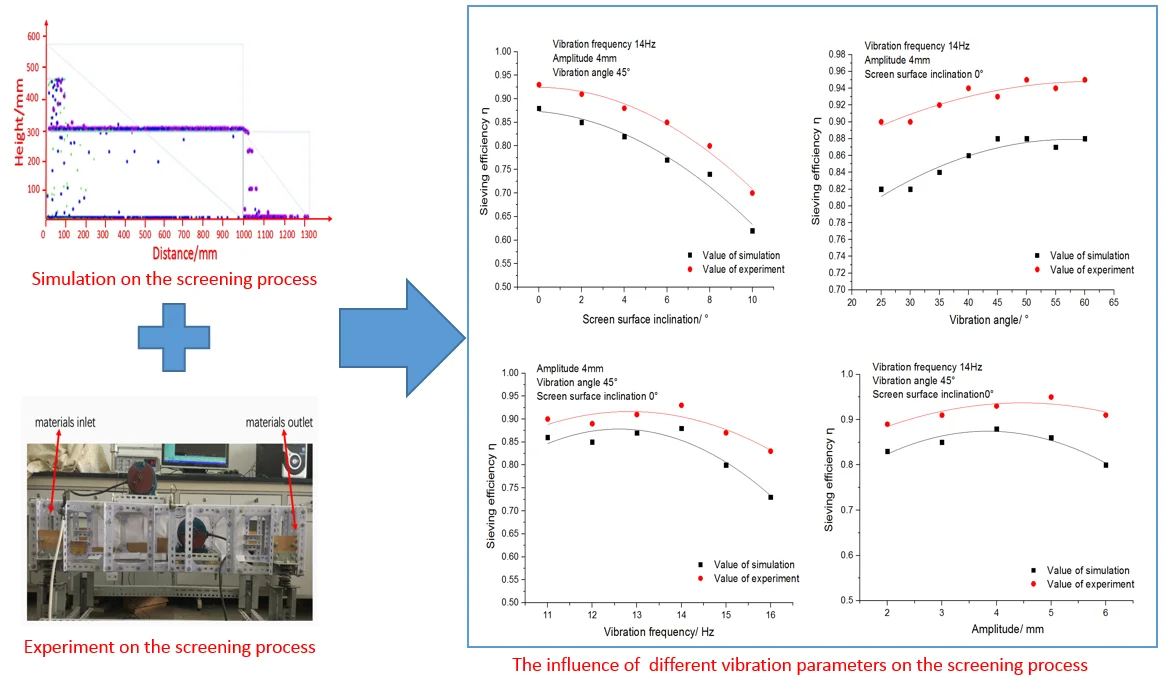
4.2.1. The influence of screen surface inclination on the screening process

Under the condition that the amplitude is 4 mm, the vibration angle is 45° and vibration frequency is 14 Hz, this paper has studied the influence of the screen surface inclination on the conveying speed and the sieving efficiency of materials. For inertial vibrating screen, the screen surface inclination is generally less than 10°, therefore, this paper aims at studying the screen surface inclination which changes in the range of 0°-10°.

(1) The influence of the screen inclination on the conveying speed of materials.

Fig. 11 shows the relationship between conveying speed of materials and screen surface inclination. It can be seen from the figure that the conveying speed of the materials increases with the increase of screen surface inclination. Therefore, the materials capacity is enhanced with the increase of screen surface inclination, which is beneficial to the discharge of materials.

(2) The influence of the screen inclination on the sieving efficiency.

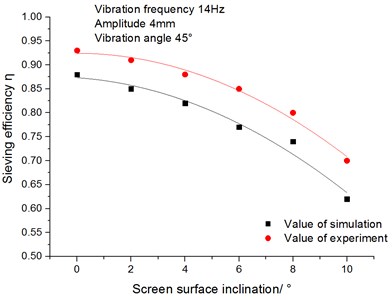
Fig. 12 shows the relationship between the sieving efficiency and screen surface inclination. As we can see from the figure, the sieving efficiency decreases with the increase of the screen surface inclination. This is mainly due to the fact that effective size of screen aperture reduced with the increase of the screen surface inclination. It is harmful to the screening of difficult-to-be-sieved particles. Consequently, the conveying speed of materials accelerates with the increase of the screen surface inclination, but the materials discharged outside without fully sieved. This leads to insufficient sieving.

Fig. 11Relationship between the conveying speed of materials and screen surface inclination

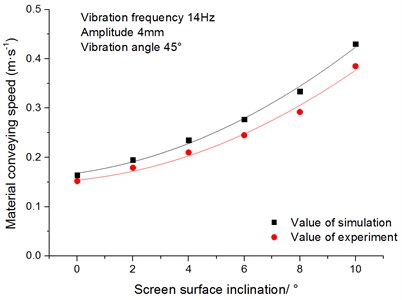
Fig. 12Relationship between sieving efficiency angle and screen surface inclination

4.2.2. The influence of vibration angle on the screening process

Under the condition that the amplitude is 4 mm, the screen surface inclination is 0° and vibration frequency is 14 Hz, this paper focuses on the influence of vibration angle on the conveying speed and the sieving efficiency of materials. In practical production and application, vibration angle generally changes from 25° to 60°. Hence, the research aims at studying the vibration angle which changes in the range of 25°-60°.

(1) The influence of vibration angle on the conveying speed of materials.

Fig. 13 shows the relationship between the conveying speed of materials and vibration angle. It can be seen from the figure that when vibration angle increases from 25° to 60°, the conveying speed of materials increases first and then decreases with the increase of vibration angle. The reasons are as follows: when the vibration angle is less than 40°, the angle between the long axis of the elliptical vibration trajectory and the screen surface is so smaller that the materials cannot be fully thrown out, materials will reciprocate on the sieve plate which results in a relatively small conveying speed of materials. This reciprocating motion improved as the vibration angle increased from 25° to 40°. So, when the vibration angle is between 20° and 40°, the conveying speed of materials increases as the angle increases. When the vibration angle is more than 40°, the angle between the long axis of the elliptical vibration trajectory and the screen surface enlarges, which leads to the enhancement of the loose effects of materials and the attenuation of conveying speed.

(2) The influence of vibration direction angle on sieving efficiency.

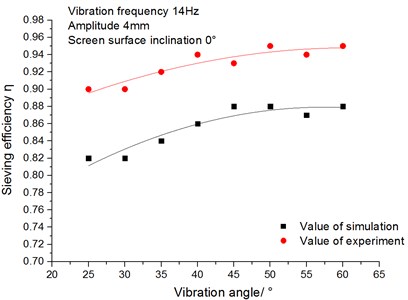
Fig. 14 shows the relationship between the sieving efficiency and the vibration angle. It can be seen from the figure that the sieving efficiency increases with the increase of the vibration angle. However, when the vibration angle increases more than 50°, the sieving efficiency increases a little with the increase of the vibration angle. The reasons are as follows: With the increase of the vibration angle, the loose effect of materials enhances and the opportunity for the materials to contact with the screen surface increases. When vibration angle exceeds 50°, it is difficult for the difficult-to-be-sieved particles to contact with the screen surface because the obstructed particles are not easy to discharge quickly, which leads to a slow growth in sieving efficiency.

Fig. 13Relationship between materials conveying speed and vibration angle

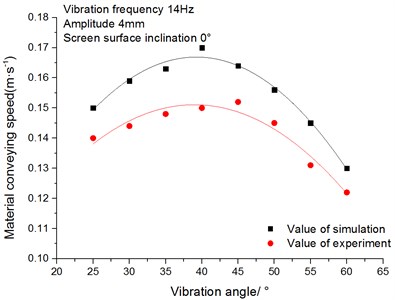
Fig. 14Relationship between sieving efficiency and vibration angle

4.2.3. The influence of vibration frequency on the screening process

Under the condition that the amplitude is 4 mm, screen surface inclination is 0° and vibration angle is 45°, this paper has studied the influence of vibration frequency on the conveying speed and sieving efficiency of the materials. Practical production and applications generally select the vibration frequency which changes from 11 Hz to 16 Hz. Hence, the research aims at studying the vibration frequency which changes from 11 Hz to 16 Hz in this paper.

(1) The influence of vibration frequency on conveying speed of materials.

Fig. 15 shows the relationship between the conveying speed and vibration frequency of materials. It can be seen from the figure that the materials’ conveying speed increases linearly with the increase of the vibration frequency when the vibration frequency increases from 11 Hz to 16 Hz.

(2) The influence of the vibration frequency on sieving efficiency.

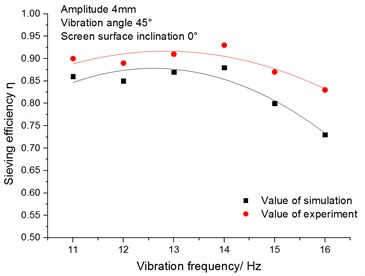
Fig. 16 shows that the relationship between the sieving efficiency and the vibration frequency. It can be seen from the figure that when the vibration frequency is less than 14 Hz, the sieving efficiency increases slowly with the increase of the vibration frequency, and the sieving efficiency decreases when the vibration frequency exceeds 14 Hz. The reasons are as follows: The collision among particles will be fiercer if the vibration frequency is large enough. The acceleration of materials’ conveying speed leads to the reduction of contact opportunities between materials and sieve plate. Hence, we can get the conclusion that the sieving efficiency for easy-to-be-sieved materials and difficult-to-be-sieved materials decreases.

Fig. 15Relationship between conveying speed of materials and vibration frequency

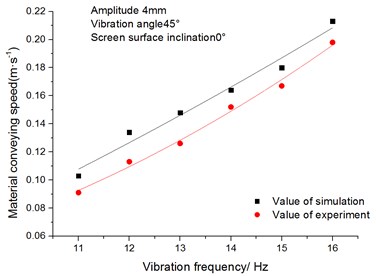
Fig. 16Relationship between sieving efficiency and vibration frequency

4.2.4. The influence of amplitude on the screening process

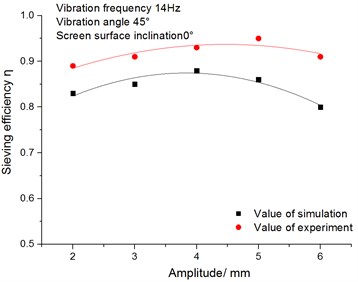
Under the condition that the vibration frequency is 14 Hz, the screen surface inclination is 0°and the vibration angle is 45°, this paper has studied the influence of amplitude on the conveying speed and sieving efficiency of the materials. In practical production and applications, the amplitude is generally not more than 10 mm. Hence, the research focuses on the amplitude which changes from 2 mm to 6 mm.

(1) The influence of amplitude on the materials’ conveying speed.

Fig. 17 shows the relationship between the conveying speed of the materials and amplitude. It can be seen from the figure that the materials’ conveying speed increases with the increase of amplitude. The larger the amplitude is, the farther the materials are thrown. So, the opportunities of random collisions among particles reduce, which makes the materials move forward quickly.

(2) The influence of the amplitude on the sieving efficiency.

Fig. 18 shows the relationship between the sieving efficiency and the amplitude. Under the condition that the amplitude is less than 5 mm, the sieving efficiency increases slowly with the increase of amplitude. On the contrary, the sieving efficiency decreases when the amplitude exceeds 5 mm. The reasons are as follows: The larger the amplitude is, the farther the materials are thrown away. The materials’ conveying speed accelerates and the opportunities for the materials to contact with the sieve plate reduce. Thus, the probability of being sieved through for the easy-to-be-sieved materials and difficult-to-be-sieved materials decreases, which leads to the reduction of the sieving efficiency.

Fig. 17Relationship between materials’ conveying speed and amplitude

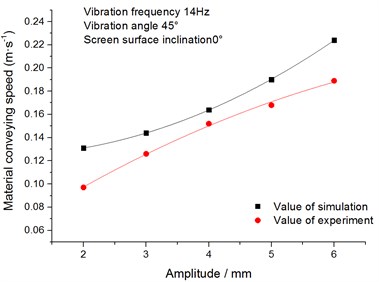
Fig. 18Relationship between sieving efficiency and amplitude

4.2.5. The analysis of differences between simulation and experimental results

Combining the above experimental results with the simulation results, we can know: for the materials’ conveying speed, the values of the simulation results are higher than that of the experimental results. However, for the sieving efficiency, the values of simulation results are lower than that of the experimental results. But the trends of the simulation results are consistent with the experimental results. The main reasons are as follows:

1) It can be assumed that no elastic deformation has occurred for the sieve plate in the EDEM simulation model. However, owing to the fact that the sieve plate installed in the test bed is affected by factors such as processing and installation, the flatness of the screen surface has also changed. And it may lead to the reduction of the materials’ conveying speed. Also, it increases the time for materials to contact with the sieve plate. As a result, the sieving efficiency increases;

2) The screen can achieve translational elliptical motion trajectory in EDEM simulation. However, owing to the fact that the screening experimental device is affected by factors such as motor installation location and installation accuracy, the motion trajectory of each position of the screen is not exactly same;

3) During the process of simulation, the materials are uniformly generated at a constant rate from the particles factory. However, it is difficult for materials to be generated uniformly at a constant rate in the practical experiment.

5. Conclusions

Considering the lack of studies about the elliptical vibrating machine, we adopt the discrete element method to simulate and analyze the screening process of the elliptical vibrating machine. A vibration screening model is particularly established on the purpose of our research to fundamentally demonstrate the novel relationships among the conveying speed, sieving efficiency and vibration parameters of the materials.

This paper has carried out EDEM simulation and screening experiment, and has investigated the influence of four vibration parameters on the screening process by controlling the single variable method. The four parameters include the screen surface inclination, vibration angle, vibration frequency and amplitude. We obtain the following conclusions:

1) The establishment of relationship curves among the parameters, the materials’ conveying speed and the sieving efficiency provides data support based on experiment and simulation for the research on the mechanism of the elliptical vibration machinery.

2) It should be noted that each individual sieving parameter has the best conveying speed and sieving efficiency. When the screen surface inclination changes from 4° to 7°, the vibration angle varies from 35° to 50°, the vibration frequency alters from 12 Hz to 15 Hz and the amplitude changes from 4 mm to 5 mm, we can ensure higher conveying speed and sieving efficiency of materials simultaneously. Furthermore, the results also provide a reference for the selection of sieving parameters.