Particle stratification of a vibrating screen with translation-swing composite motion

Shen, Guolang; Tong, Xin

doi:10.21595/jve.2019.20683

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 May 2020

Check for updates

Particle stratification of a vibrating screen with translation-swing composite motion

Guolang Shen¹

Xin Tong²

^{1, 2}School of Mechanical Engineering and Automation, Huaqiao University, Xiamen, 361021, China

²School of Mechanical and Automation engineering, Fujian University of Technology, Fuzhou, 350118, China

Corresponding Author:

Xin Tong

Cite the article Download PDF

Downloads 1397

WoS Core Citations 1

CrossRef Citations 1

Abstract

With the development of science and technology, more and more demand was proposed in the sieving industry. The sieving theory has been used to optimize parameters of vibrating screen to achieve a higher screening efficiency. Perfecting the sieving theory was became the main goal of most scholars to study the vibrating screen. Stratification as part of sieving theory research, the screening process and screening result was deeply influenced by stratification. In this paper, the sedimentation difference was defined to make the stratification became a numerical description. The discrete element method (DEM) has been used to simulate the screening process about the vibrating screen with translation-swing composite motion. The relationship between screening efficiency and sedimentation difference under each parameter is established and the effect of stratification on screening efficiency is studied under various single parameter conditions including vibration frequency, amplitude, vibration direction angle, swinging frequency, and swinging angle. The conclusions are: sedimentation difference is closely related to screening efficiency, the screening efficiency had obviously a positive correlation with the sedimentation difference. Combined with the value of the sedimentation difference, a better positive stratification is meaningful to the screening process and screening efficiency.

Particle stratification of a vibrating screen with translation-swing composite motion

Highlights

The screening process and screening result was deeply influenced by stratification, the sedimentation difference was defined to make the stratification became a numerical description
The relationship between screening efficiency and sedimentation difference under each parameter is established and the effect of stratification on screening efficiency is studied under various single parameter conditions
The sedimentation difference is closely related to screening efficiency, the screening efficiency had obviously a positive correlation with the sedimentation difference

1. Introduction

Sieving machinery is used to classify particle material by particle size in the industry. The law of the screening process is extremely complicated. The screening process is regarded as the intricacies of particle-particle and particle-machine interactions. The influence of these interactions on the screening process affected the screening efficiency and the value of the product. The screening process can be divided into four parts through the previous researches: (1) Looseness: the void space that occurs between particles which are rebounded by the sieve plate. (2) Stratification: fine particles through the coarse particles to approach the screen surface. (3) Collision: the particles near the screen surface are defined as the collision particles, some of these particles impact the sieve wires and some pass through the sieve mesh. (4) Penetration: the particles pass through the apertures to become undersize particles. By these four parts, the particles’ classification was completed.

Stratification is the main process of the sieving process, scholars have done a lot of work for the stratification. Mosby [1, 2] used some factors to describe the phenomenon of material stratification, and put forward some viewpoints that are instructive to screening: (1) stratification is easier to happen when distribution of the particle size is very spread; (2) stratification is more difficult when the distribution of the particle size is concentrated; (3) particle size has a bigger influence on stratification than particle density and shape; (4) it is not easier to stratify for wet material or material mixed with fluid. The research of Lawrence and Beddow [3] shows that stratification is best when the content of fine particles is at 15 to 30 percent, and stratification almost does not occur when the content of fine particles is at 60 percent or more. Chen Yanhua and Tong Xin [4, 5] stated briefly that stratification in sieving is the process that fine particles passed through coarse particles and reached to screen surface when the screen is vibrating. Forming fine particles group near the screen surface is the result of stratification. The fine particles are closer to the screen surface, the easier they can penetrate to screen. Rao [6] has presented several factors that influence the stratification process, such as particle size, shape, and density. In these articles, stratification is defined as the content of fine particles in a certain thickness of material on the screen surface. It can’t really reflect the stratification by using this method because they didn't take the distance between the fine particles with the screen surface into consideration.

When the particle is vibrated, coarse particles move upward and fine particles move downward, which is referred to as the Brazil nut effect [7, 8]. Stratification configuration of Brazil fruit under the ideal condition like the Fig. 1(a), it is the stratification configuration we want to achieve most. Fig. 1(b) is the stratification configuration of Anti Brazil fruit under ideal condition, coarse particles move downward and fine particles move upward. This stratification configuration leads to the fine particles can’t reach to screen surface, so we should avoid the appearance of stratification configuration of Anti Brazil fruit. There is another stratification configuration that likes a sandwich, the coarse particles are sandwiched between the fine particles. This stratification configuration can be described as Fig. 1(c). These three stratification configurations are layered under ideal conditions. In the actual sieving process, the particles are randomly distributed (Fig. 1(d)). The significance of stratification is to make more fine particles closer to the screen surface [9, 10].

Fig. 1Stratified configurations

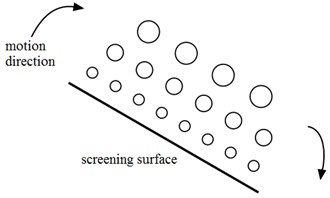
a) Stratification configuration of Brazil fruit under ideal condition

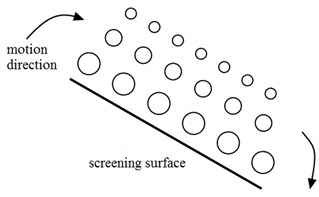
b) Stratification configuration of Anti Brazil fruit under ideal condition

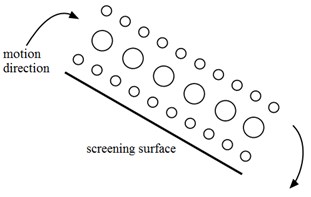
c) Sandwich configuration under ideal condition

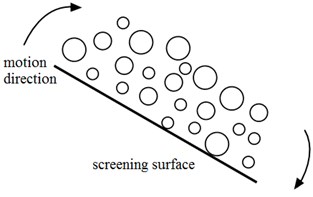
d) Stratified configurations under actual screening condition

2. Simulation

2.1. Definition and calculation method of sedimentation difference

As mentioned above, the significance of stratification is to make more fine particles closer to the screen surface, so the distance between particles to screen surface should be calculated, stratification sedimentation coefficient and sedimentation difference were proposed in this paper. To count the particle content according to the distance between the particle and the screen surface, when the particle content is determined, the distance between the screen surface and the layer is also determined. In the screening process, most of the particles under the bottom layer were contacted with the screen surface and the particles over the top layer had no effect on stratification. Accordingly, the layer that particle content is between 10 percent and 90 percent was considered as a material bed, particle content is 10 percent was called the bottom layer of material bed, and particle content is 90 percent was called the top layer of the material bed, it was shown in Fig. 2.

Fig. 2Section of the material bed

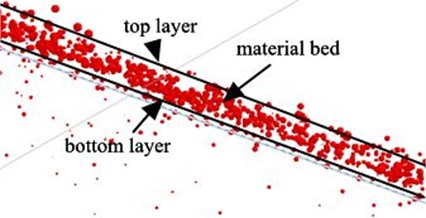
In the material bed, the stratification sedimentation coefficient is defined as the ratio of the mean distance between fine particles under relative separated particle size and all particles from themselves to the bottom layer of material bed on the screen. According to experience, the 0.7 times of aperture size often been used as relative separated particle sizes to calculate the screening efficiency, and there is high screening efficiency when it is used for dealing with difficult-to-screen material. Stratification sedimentation coefficient $S$ is given by Eq. (1):

1

S = \frac{(H_{1} - H_{a})}{(H - H_{a})} \times 100 %,

where $H_{1}$ is mean distance from fine particles under relative separated particle size to the screen surface. $H_{a}$ is the distance from the bottom layer of the material bed to the screen surface. $H$ is the mean distance from all particles to the screen surface.

The sedimentation difference is based on the stratification sedimentation coefficient. To calculate the mean distance of coarse particles over relative separated particle size and fine particles under relative separated particle size from themselves to the bottom layer of material bed, and divided by the mean distance of all particles from themselves to the bottom layer of material bed on the screen. Sedimentation difference $S D$ is using Eq. (2):

2

S D = \frac{- (H_{1} - H_{2})}{(H - H_{a})} \times 100 %,

where $H_{1}$ is the mean distance from fine particles over relative separated particle size to the screen surface. $H_{2}$ is the mean distance from coarse particles under relative separated particle size to the screen surface. $H$ is the mean distance from all particles to the screen surface. $H_{a}$ is the distance from the bottom layer of the material bed to the screen surface.

In order to facilitate statistics, the sedimentation difference $S D$ is also using Eq. (3):

3

S D = S_{1} - S_{2},

where $S_{1}$ is mean the stratification sedimentation coefficient of the coarse particles, $S_{2}$ is mean the stratification sedimentation coefficient of the fine particles.

In the software of DEM, the position and quality information of each particle can be obtained in the three-dimensional coordinate system, then calculated the height of each particle from the screen surface by using the following formulas:

4

t a n α = \frac{z_{1}}{x},

5

z_{1} + z_{2} = z,

6

c o s α = \frac{h}{z_{2}},

7

h = (z - x t a n α) c o s α,

where $α$ for the slope angle of the screen surface, $h$ for the height of particles from screen surface, $x$ and $z$ for the $X$ -axis and $z$ -axis coordinates of particles in the three-dimensional coordinate system, respectively.

Fig. 3The height of particle to screen surface

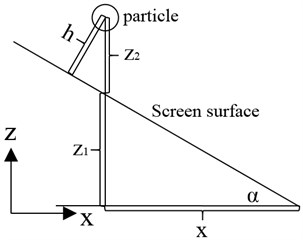
The height of each particle can be calculated by using the above method, $H$ was determined by averaging the height of all particles, and $H_{1}$ was determined by averaging the height of fine particles under relative separated particle size. $H_{a}$ is the distance from the bottom layer of material bed to the screening surface, and particle content is 10 percent was called the bottom layer of material bed, we can use the following steps to determine the $H_{a}$ . Firstly, calculate the total mass of particles on the screen surface. Secondly, sort the height from small to large. Thirdly, summed the particle mass according to height. When the sum equals one-tenth of the total mass, $H_{a}$ was determined and equals to the height of the last particle.

Combine with the value of the sedimentation difference, stratification called ‘positive stratification’ when the value is greater than 0, this stratification corresponds to the stratification configuration of Brazil fruit; stratification called ‘negative stratification’ when the value is lee than 0, this stratification corresponds to the stratification configuration of Anti Brazil fruit.

We can use Eq. (8) and Eq. (9) to calculate the stratification sedimentation coefficient of the coarse particles and fine particles. Finally, SD can be obtained by subtraction with the Eq. (3):

8

S^{j} = \frac{(H_{1}^{j} - H_{a}^{j})}{(H^{j} - H_{a}^{j})} \times 100 %,

9

S = \frac{\sum_{j = 1}^{9} S^{j}}{9},

where $j$ for the number of points. Because of the screen surface have sinusoidal vibration with periodically change, and the stratification sedimentation coefficient was influenced by the motion of the screen surface, so we choose a cycle randomly, and divided the cycle into nine points, then calculated the stratification sedimentation coefficient of these nine points and average out their values, the average value was treated as the stratification sedimentation coefficient.

2.2. The discrete element method used in the simulation

In recent years, the discrete element method (DEM) has been used to model the motion and effect of a large number of particles. Many scholars have achieved great success by using the DEM to study the vibrating screen. P. W. Cleary [11-13] has made a great contribution to the development of the vibrating screen, he applied the DEM to model and affect a large number of small particles to capture the spherical particle separation on an inclined flat screen, he has proved that the DEM has a good efficacy to simulate the motion of particles on the sieving machinery. Tong [14, 15] has built the 3D model of vibrating screen, then used the model analyzed the screening efficiency and screening process in different parameters with a different pattern of vibration. So the data difficult to obtain in the actual sieving process can be obtained by using the simulation based on the discrete element method.

The DEM apply Newton’s second law of motion to calculate the forces and acceleration acting on each particle [16, 17]. Using the dynamic relaxation method or static relaxation iteration methods, new particle states are obtained. Then all of the forces and moments produced by the collisions are summed up. The resulting equations of motion are integrated, as follows:

10

{\dot{x}}_{i} = v_{i}, {\dot{v}}_{i} = \frac{\sum_{j} F_{i j}}{m_{i}} + g,

11

{\dot{θ}}_{i} = ω_{i}, {\dot{ω}}_{i} = \frac{\sum_{j} M_{i j}}{I_{I}},

where $x_{i}$ , $v_{i}$ , $F_{i j}$ are the displacement, velocity and collisional forces of the particle which number is $i$ , $θ_{i}$ , $ω_{i}$ , $M_{i j}$ , $I_{i}$ are angular displacement, rotational velocity, resultant moment and the moment of inertia of the particle which number is $i$ . So the position information needed in this paper can be obtained by using DEM easily.

2.3. Simulation model and condition

The vibrating screen of translation-swing composite motion is the combination of sinusoidal translation and sinusoidal rotation [18]. Decomposing the motion, we can get the sinusoidal translation is shown as follow:

12

\begin{array}{l} A_{x} = A \cdot s i n θ \cdot s i n (ω t - a_{x}), \\ A_{y} = A \cdot c o s θ \cdot s i n (ω t - a_{y}), \end{array}

where $A_{x}$ and $A_{y}$ are the displacements in the horizontal and vertical directions, $a_{x}$ and $a_{y}$ are the phase angles between the exciting force and the displacements in the horizontal and vertical directions, $ω$ is the angular velocity, $A$ is the amplitude of vibration, $θ$ is the vibrating direction angle. So the vibration is determined by the vibration frequency, amplitude, and vibrating direction angle.

The sinusoidal rotation is shown as follow:

13

φ = A_{φ} s i n ψ t,

where $φ$ is the swinging displacement, $A_{φ}$ is the amplitude of swinging displacement, $ψ$ is the swinging frequency. So the sinusoidal rotation is determined by the swinging frequency and swinging angle.

In conclusion, the vibrating screen of translation-swing composite motion is determined by the vibration frequency, amplitude, vibrating direction angle, swinging frequency, and swinging angle.

A 3D model was set up to simulate particle flow on a vibrated inclined screen, the initial parameters were shown in Fig. 4, and the angle of screen inclination is 21 degrees, screen box is 160 mm long, 30.5 mm wide and 80 mm high. Combined with the size distribution of sands used in the industry, mixture of two different size particles is employed which consists of a bimodal normal distribution with individually mean diameters of 0.5 and 1.0 mm and uniformly standard deviation of 0.55 in the paper. The total number of particles is 10000 in every simulation, and particles generate rate is 16666 particles/s. Other conditions and parameters are listed in Table 1 and Table 2.

Fig. 4Simulation model

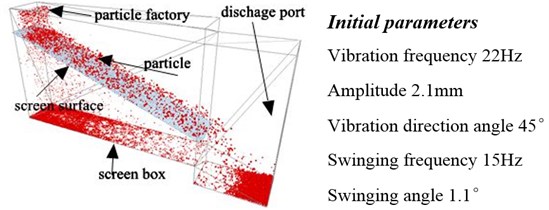
Table 1Material properties

Material properties	Poisson’s ratio	Shear modulus	Density
Particle	0.3	2.3e+07 Pa	2678 kg/m³
Screen surface	0.29	7.992e+10 Pa	7861 kg/m³

Table 2Collision properties

Collision properties	Coefficient of restitution	Coefficient of static friction	Coefficient of rolling friction
Particle-particle	0.1	0.545	0.01
Particle-geometry	0.2	0.5	0.01

3. Results and discussion

As a criterion for evaluating screening efficiency ( $S E$ ), $η$ is described as:

14

η_{d} = (\frac{m_{< d}^{u}}{m_{< d}} - \frac{m_{> d}^{u}}{m_{> d}}) \times 100 %,

where $m_{< d}$ , $m_{> d}$ are the mass of particles whose diameters are smaller than $d$ and bigger than $d$ . $m_{< d}^{u}$ , $m_{> d}^{u}$ are the mass of particles whose diameters are smaller than $d$ and bigger than $d$ and their position is under the screen surface, $η_{d}$ is screening efficiency of the separation size is $d$ .

The relationship between screening efficiency and sedimentation different was systematically analyzed by the comprehensive methods of intuitive analysis and mathematical statistics analysis.

3.1. Intuitive analysis

The method of comparing the relationship between screening efficiency and sedimentation different by their graphs is called intuitive analysis. Their trends can be analyzed intuitively by this method.

3.1.1. Vibration frequency

Numerous studies had shown that vibration frequency had a major influence on particles bounce. Vibration frequency as one of the simulation conditions that we set at 16 Hz, 18 Hz, 20 Hz, 22 Hz, 24 Hz, and 26 Hz is used to obtain variation laws of sedimentation different. Compared the screening efficiency with the sedimentation different in Fig. 5, it concluded that the two curves of the sedimentation difference and screening efficiency change similarly in whole intervals, although they show an opposite tendency in a very small interval, it can be proved that improve the sedimentation difference could promote the screening efficiency. The sedimentation difference changes with several values of vibration frequency, and it reaches the maximum when the vibration frequency is 18 Hz. The sedimentation difference increases with vibration frequency when vibration frequency is less than 18 Hz, and it decreases with vibration frequency when vibration frequency is greater than 18 Hz. It can be concluded that sedimentation is best when vibration frequency reaches a certain point. When the vibration frequency changes, combined with the value of the sedimentation difference, positive stratification appeared in the interval about 16 Hz to 26 Hz. In this interval, stratification is beneficial for the sieving process.

Fig. 5Comparison between sedimentation difference and screening efficiency about different vibration frequency

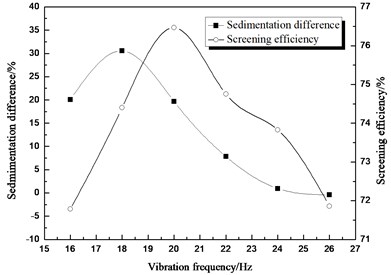
Fig. 6Comparison between sedimentation difference and screening efficiency about different amplitude

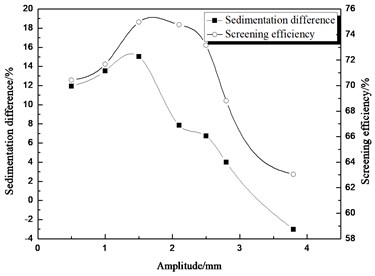
3.1.2. Amplitude

Generally, the amplitude has a similar influence on screening efficiency with the vibration frequency. Amplitude is one of the simulation conditions that we set at 0.5 mm, 1.0 mm, 1.5 mm, 2.1 mm, 2.5 mm, 2.8 mm, and 3.8 mm. Compared the screening efficiency with the sedimentation different in Fig. 6, it concluded that the two curves of the sedimentation difference and screening efficiency change similarly in whole intervals, it can be proved that improve the sedimentation difference could promote the screening efficiency. The sedimentation difference changes with several values of amplitude, and it reaches the maximum when the amplitude is 1.5 mm. The sedimentation difference increases with amplitude when the amplitude is less than 1.5 mm, and it decreases with amplitude when the amplitude is greater than 1.5 mm. When the amplitude changes, combined with the value of the sedimentation difference, positive stratification appeared in the interval about 0.5 mm to 3.5 mm.

3.1.3. Vibrating direction angle

Vibrating direction angle has an influence on the force direction of the particle over the screen surface, and it is related to the time of the screening process. The value of the vibrating direction angle should not be too small, because the particles stayed on the screen surface for a long time and the handling capacity of the vibration screen became small. Vibrating direction angle as one of the simulation conditions that we set at 31°, 36°, 45°, 56°, 61°, 68° and 81°. Compared the screening efficiency with the sedimentation different in Fig. 7, it concluded that the two curves of the sedimentation difference and screening efficiency change similarly in whole intervals, it can be proved that improve the sedimentation difference could promote the screening efficiency. The screening efficiency and sedimentation difference change with several values of vibrating direction angle, and it decreases with vibrating direction angle in the whole interval. When the vibrating direction angle changes, combined with the value of the sedimentation difference, positive stratification appeared in the whole section. For negative stratification, it does not appear within an acceptable range of the vibrating direction angle, but that doesn’t mean it won’t appear when the vibrating direction angle is the other value.

Fig. 7Comparison between sedimentation difference and screening efficiency about different vibrating direction angle

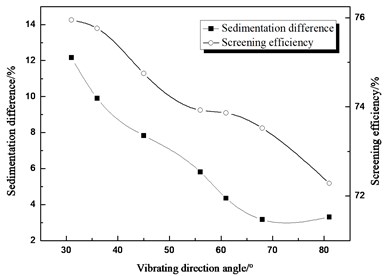
Fig. 8Comparison between sedimentation difference and screening efficiency about the different swinging frequency

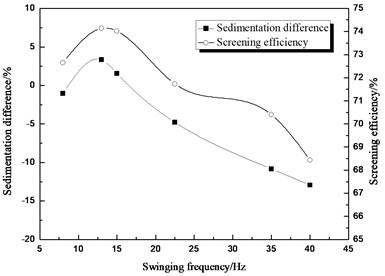
3.1.4. Swinging frequency

Similar to vibration frequency, swinging frequency has an effect to decide the activity of the particle over the screen surface. Swinging frequency as one of the simulation conditions that we set at 8 Hz, 13 Hz, 15 Hz, 22.5 Hz, 35 Hz and 40 Hz. Compared the screening efficiency with the sedimentation different in Fig. 8, it concluded that the two curves of the sedimentation difference and screening efficiency change similarly in whole intervals, it can be proved that improve the sedimentation difference could promote the screening efficiency. The sedimentation difference changes with several values of swinging frequency, and it reaches the maximum when the swinging frequency is 13 Hz. The sedimentation difference increases with swinging frequency when swinging frequency is less than 13 Hz, and it decreases with swinging frequency when swinging frequency is greater than 13 Hz. It can be concluded that sedimentation is best when the swinging frequency reaches a certain point. When the swinging frequency changes, combined with the value of the sedimentation difference, positive stratification appeared in the interval about 10 Hz to 15 Hz.

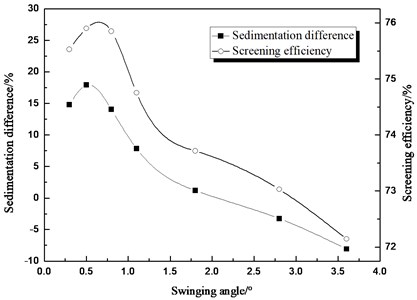
3.1.5. Swinging angle

The swinging angle plays a decisive role in the swinging amplitude, thus it directly affects the quality of the stratification. Swinging angle as one of the simulation conditions that we set at 0.3°, 0.5°, 0.8°, 1.1°, 1.8°, 2.8° and 3.6°. Compared the screening efficiency with the sedimentation different in Fig. 9, it concluded that the two curves of the sedimentation difference and screening efficiency change similarly in whole intervals, it can be proved that improve the sedimentation difference could promote the screening efficiency. The sedimentation difference changes with several values of the swinging angle, and it reaches the maximum when the swinging angle is 0.5°. The sedimentation difference increases with the swinging angle when the swinging angle is less than 0.5°, and it decreases with swinging angle when the swinging angle is greater than 0.5°. It can be concluded that sedimentation is best when the swinging angle reaches a certain point. When the swinging angle changes, combined with the value of the sedimentation difference, positive stratification appeared in the interval about 0.3° to 2.0°.

Fig. 9Comparison between sedimentation difference and screening efficiency about the different swinging angle

3.2. Mathematical statistics analysis

Using the correlation coefficients to describe the linear dependence of screening efficiency and sedimentation different should better reflect their relationship.

The correlation coefficient of two random variables is a measure of their linear dependence. If each variable has $N$ scalar observations, then the Pearson correlation coefficient is defined as follow:

15

ρ (A, B) = \frac{1}{N - 1} \sum_{i = 1}^{N} (\frac{A_{i} - μ_{A}}{σ_{A}}) (\frac{B_{i} - μ_{B}}{σ_{B}}),

where $μ_{A}$ and $σ_{A}$ are the mean and standard deviation of $A$ , respectively, $μ_{B}$ and $σ_{B}$ are the mean and standard deviation of $B$ . Alternatively, you can define the correlation coefficient in terms of the covariance of $A$ and $B$ :

16

ρ (A, B) = \frac{c o v (A, B)}{σ_{A} σ_{B}} .

The correlation coefficient matrix of two random variables is the matrix of correlation coefficients for each pairwise variable combination:

17

R = (\begin{array}{l} ρ (A, A) & ρ (A, B) \\ ρ (B, A) & ρ (B, B) \end{array}) .

Since $A$ and $B$ are always directly correlated to themselves, the diagonal entries are just 1, that is:

18

R = (\begin{matrix} 1 & ρ (A, B) \\ ρ (B, A) & 1 \end{matrix}) .

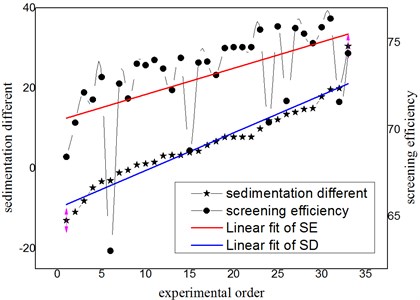
The correlation is very strong when the value of the correlation coefficient is close to 1. Meanwhile, the value of the correlation coefficient does not change with the order of the data. In this paper, the number of our samples is 33 and the correlation coefficient is 0.5211. From the data analysis, the screening efficiency was middlingly correlated with sedimentation different.

In addition, put all data of the screening efficiency and sedimentation different together, and arranged them in order of sedimentation different from small to large. Compared to the growing trend of sedimentation different and screening efficiency by their trend lines (Fig. 10). It concluded that their growth trends are similar.

Fig. 10Comparison between screening efficiency and sedimentation different

4. Conclusions

From this work, we can get the following conclusion:

1) The definitions of stratification sedimentation coefficient and sedimentation difference have been proposed and proposed a method to calculate the stratification sedimentation coefficient and sedimentation difference. Through the value of sedimentation difference, the stratification should be understood better. It can enrich the mechanism of stratification and provide some thoughts for the research of stratification.

2) In this paper, the relationship between the sedimentation differences with the screening efficiency was analyzed. After the study, it can be found that improve the sedimentation difference could promote the screening efficiency and the screening efficiency had obviously a positive correlation with the sedimentation difference. It proved that the stratification is meaningful to the screening efficiency.

3) The vibrating screen of translation-swing composite motion as a new type of vibrating screen, for our feeding sample, we can achieve a screening efficiency about 76 %. The optimal vibration parameters are: vibration frequency is 20 Hz, the amplitude is 1.5mm, vibrating direction angle is 31°, swinging frequency is 15 Hz, and swinging angle is 0.5°.

Anyway, it is not enough to improve the screening efficiency by research the law of stratification only, a better stratification is the key to improve the screening efficiency, and this work hopes to continuously improve the screening theory and further breakthroughs.

References

Mosby J., De Silva S. R., Enstad G. G. Segregation of particulate materials – mechanisms and testers. Powder and Particle, Vol. 14, 1996, p. 31-43.

Search CrossRef
Mosby J., Enstad G. G., et al. Segregation of particulate solids: processes, mechanisms, and counteractions. KONA, Vol. 14, 1996, p. 31-43.

Publisher
Lawrence L. R., Beddow J. K. Powder segregation during die filling. Powder Technology, Vol. 2, Issue 5, 1969, p. 253-259.

Publisher
Chen Y., Tong X. Modeling screening efficiency with vibrational parameters based on DEM 3D simulation. Mining Science and Technology (China), Vol. 20, Issue 4, 2010, p. 615-620.

Publisher
Chen Yan Hua, Tong X. Application of the DEM to screening process: a 3D simulation. Mining Science and Technology, Vol. 19, Issue 4, 2009, p. 493-497.

Publisher
Venkoba Rao B., Kapur P. C., Konnur R. Modeling the size-density partition surface of dense-medium separators. International Journal of Mineral Processing, Vol. 72, Issues 1-4, 2003, p. 443-453.

Publisher
Rosato A., Strandburg K. J., Prinz F., et al. Why the Brazil nuts are on top: Size segregation of particulate matter by shaking. Physical Review Letters, Vol. 58, Issue 10, 1987, p. 1038.

Publisher
Hong D. C., Quinn P. V., Luding S. Reverse Brazil nut problem: competition between percolation and condensation. Physical Review Letters, Vol. 86, Issue 15, 2001, p. 3423-3426.

Publisher
Cleary P. W. Large scale industrial DEM modelling. Engineering Computations, Vol. 21, Issues 2-4, 2004, p. 169-204.

Publisher
Soldinger M. Transport velocity of a crushed rock material bed on a screen. Minerals Engineering, Vol. 15, Issues 1-2, 2002, p. 7-17.

Publisher
Cleary P. W., Sawley M. L. DEM modelling of industrial granular flows: 3D case studies and the effect of particle shape on hopper discharge. Applied Mathematical Modelling, Vol. 26, Issue 2, 2002, p. 89-111.

Publisher
Cleary P. W., Sinnott M. D. Simulation of particle flows and breakage in crushers using DEM: Part 1 – Compression crushers. Minerals Engineering, Vol. 74, 2015, p. 178-197.

Publisher
Cleary P. W., Sinnott M. D., Morrison R. D. Separation performance of double deck banana screens – Part 1: Flow and separation for different accelerations. Minerals Engineering, Vol. 22, Issue 14, 2009, p. 1218-1229.

Publisher
Wang G., Tong X. Screening efficiency and screen length of a linear vibrating screen using DEM 3D simulation. Mining Science and Technology (China), Vol. 21, Issue 3, 2011, p. 451-455.

Publisher
Xiao J., Tong X. Particle stratification and penetration of a linear vibrating screen by the discrete element method. International Journal of Mining Science and Technology, Vol. 22, Issue 3, 2012, p. 357-362.

Publisher
Dong K. J., Yu A. B., Brake I. DEM simulation of particle flow on a multi-deck banana screen. Minerals Engineering, Vol. 22, Issue 11, 2009, p. 910-920.

Publisher
Fernandez J. W., Cleary P. W., Sinnott M. D., et al. Using SPH one-way coupled to DEM to model wet industrial banana screens. Minerals Engineering, Vol. 24, Issue 8, 2011, p. 741-753.

Publisher
Xiao J., Tong X. Characteristics and efficiency of a new vibrating screen with a swing trace. Particuology, Vol. 11, Issue 5, 2013, p. 601-606.

Publisher

Cited by

Dynamic characteristics of LIWELL flip-flow screen panel and particle movement

Baoxing Chen | Chi Yu | Sanpeng Gong | Xinwen Wang

(2021)

About this article

Received

24 March 2019

Accepted

07 November 2019

Published

15 May 2020

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/jve.2019.20683

Keywords

vibrating screen

stratification

sedimentation difference

screening efficiency

sieving theory

Acknowledgements

The authors gratefully acknowledged the support from the National Natural Science Foundation of China (51175190), Key projects of Fujian provincial youth natural fund (JZ160460), the 51st scientific research fund program of Fujian University of Technology (GY-Z160139) and Subsidized Project for Postgraduates’ Innovative in Scientific Research of Huaqiao University (1601103005).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 03 14

Dynamic characteristics analysis of a novel vibrating screen based on electromechanical coupling simulation

Zhenqian Wang, Jida Wu, Zhaojun Kou, Yuanming Zhang, Chusheng Liu

Research article

2023 02 11

Dynamic characteristics analysis of a circular vibrating screen

Yuanchen Wang, Zhenqian Wang, Min Zhang, Bowen Xu, Yunhao Song

Research article

2019 12 31

DEM simulation and experimental study on the screening process of elliptical vibration mechanical systems

Bing Chen, Jiwei Yan, Wei Mo, Chuanlei Xu, Lijie Zhang, Kumar K Tamma

Research article

2019 02 15

Performance optimization of banana vibrating screens based on PSO-SVR under DEM simulations

Zhanfu Li, Kunyuan Li, Xiaole Ge, Xin Tong

G. Shen and X. Tong, “Particle stratification of a vibrating screen with translation-swing composite motion,” Journal of Vibroengineering, Vol. 22, No. 3, pp. 498–508, May 2020, https://doi.org/10.21595/jve.2019.20683

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2019.20683
UR  - https://doi.org/10.21595/jve.2019.20683
TI  - Particle stratification of a vibrating screen with translation-swing composite motion
T2  - Journal of Vibroengineering
AU  - Tong, Xin
AU  - Shen, Guolang
PY  - 2020
DA  - 2020/05/15
PB  - JVE International Ltd.
SP  - 498-508
IS  - 3
VL  - 22
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

@article{Tong_2020,
	doi = {10.21595/jve.2019.20683},
	url = {https://doi.org/10.21595/jve.2019.20683},
	year = 2020,
	month = {may},
	publisher = {{JVE} International Ltd.},
	volume = {22},
	number = {3},
	pages = {498--508},
	author = {Xin Tong and Guolang Shen},
	title = {Particle stratification of a vibrating screen with translation-swing composite motion},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]X. Tong and G. Shen, “Particle stratification of a vibrating screen with translation-swing composite motion,” Journal of Vibroengineering, vol. 22, no. 3, pp. 498–508, May 2020, doi: 10.21595/jve.2019.20683.

Copy IEEE

Copied to clipboard!

Tong, Xin, and Guolang Shen. “Particle Stratification of a Vibrating Screen with Translation-Swing Composite Motion.” Journal of Vibroengineering 22, no. 3 (May 15, 2020): 498–508. https://doi.org/10.21595/jve.2019.20683.

Copy Chicago

Copied to clipboard!

Particle stratification of a vibrating screen with translation-swing composite motion

Abstract

Highlights

1. Introduction

2. Simulation

2.1. Definition and calculation method of sedimentation difference

2.2. The discrete element method used in the simulation

2.3. Simulation model and condition

3. Results and discussion

3.1. Intuitive analysis

3.1.1. Vibration frequency

3.1.2. Amplitude

3.1.3. Vibrating direction angle

3.1.4. Swinging frequency

3.1.5. Swinging angle

3.2. Mathematical statistics analysis

4. Conclusions

References

Cited by

About this article

Related Articles