Dynamic characteristics analysis of a circular vibrating screen

1. Introduction

Vibrating screen is the key equipment in coal preparation industry, and it uses the vibration of the porous screen surface to complete the particle separation, so as to achieve the purpose of raw coal classification, dehydration, disintermediation, desliming, etc. [1, 2]. The use of vibrating screen to screen coal can effectively improve the clean utilization rate of coal and achieve energy conservation, emission reduction and sustainable development [3, 4].

However, during the operation of the vibrating screen, the vibration exciters will produce strong alternating load on the screen body, which will lead to side plates deformation, beam fracture and other failures of the screen body, affecting the structural reliability and reducing the working life of the vibrating screen [5, 6].

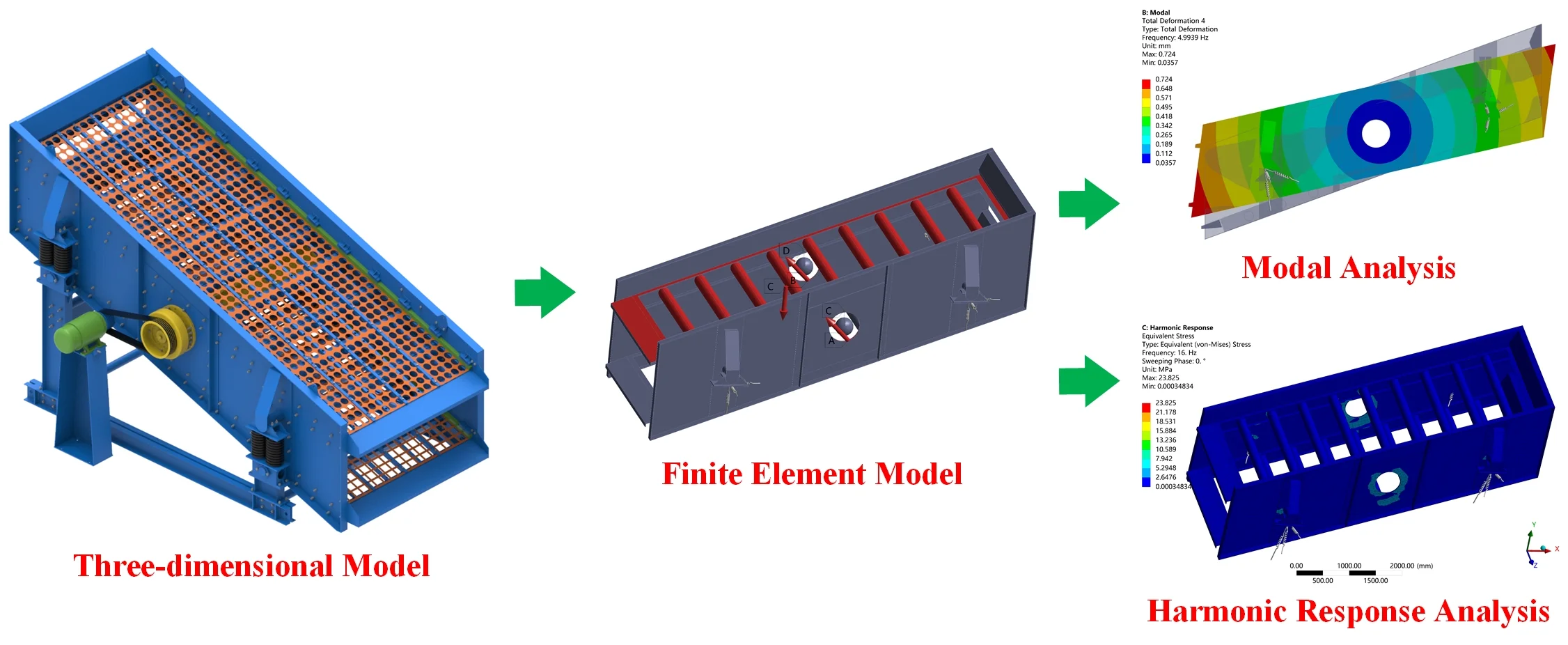
In this study, the 2460 double-layer circular vibrating screen is taken as the research object. The three-dimensional model of the vibrating screen is established in Creo, and the modal analysis and harmonic response analysis are carried out in ANSYS Workbench to study the structural strength and stiffness of the vibrating screen.

2. Three-dimensional modeling

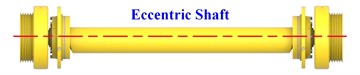
The 2460 double-layer circular vibrating screen is mainly composed of side plate, discharge end, baffle, screen mesh, spring, vibration exciters and other parts. The three-dimensional model of this vibrating screen is established in the 3D software Creo, as shown in Fig. 1. The motor drives the vibration exciters to rotate together through the belt, so as to generate the exciting force, which drives the whole screen body to perform periodic reciprocating vibration, and its motion trajectory is approximately circular.

The main shaft of the vibration exciter is designed as an eccentric shaft, so that the exciting force is evenly distributed on the whole shaft to avoid concentrated load. The bearing capacity of the main shaft is more reasonable, which can improve the service life and structural reliability of the main shaft, as shown in Fig. 2. The elastic connection between the motor and the exciter is achieved by a belt, and no additional elastic coupling is required, making the structure simpler and more reliable. The screen surface adopts the modular design, which is fixed on the support beams by pressing woods and strips, so it can be replaced according to the working conditions and has good applicability. The screen body supported by rubber spring has the advantages of low noise, small fluctuation in resonance area, and stable vibration.

Fig. 1Three-dimensional model of 2460 double-layer circular vibrating screen: 1 – baffle; 2 – side plate; 3 – spring; 4 – motor; 5 – motor support; 6 – belt; 7 – vibration exciter; 8 – spring support; 9 – base; 10 – discharge end; 11 – screen mesh; 12 – pressing wood; 13 – pressing strip

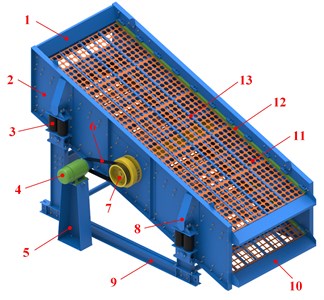
Fig. 2Structure of main shaft

3. Establishment of finite element model

Before the finite element analysis, the finite element model of the vibrating screen needs to be established in ANSYS Workbench. In view of the complex structure of 2460 double-layer circular vibrating screen, if the simulation analysis is carried out according to the actual model, the calculation amount and the calculation time will increase. Therefore, in this study, the vibrating screen model has been simplified under the premise of allowable error. Some parts and structural details that have less impact on structural strength are omitted, such as screen mesh, bolts, bolt holes and chamfers, etc. Other parts are bonded together to form a rigid frame structure, as shown in Fig. 3(a). The main components of the vibrating screen are structural steel Q345 with good mechanical properties, the material performance parameters are shown in Table 1.

After simplification, the model of vibrating screen needs to be meshed. In ANSYS Workbench, the success rate and quality of mesh are closely related to the structure shape. The more irregular the structure shape is, the easier the mesh is to fail, and the worse the mesh quality is. Therefore, this study uses a variety of methods to mesh the 2460 double-layer circular vibrating screen. Sweep mesh method is used for the parts with regular shape, such as support beams and side plates, the mesh quality is higher. Automatic mesh method is used for the irregular shaped parts, such as reinforcing plates, discharge end, and baffle, which has a higher success rate. The size of mech element is set to 50 mm, and the effect of mesh division is shown in Fig. 3(a). The mesh includes 374065 nodes and 125627 elements. Skewness is an evaluation index to measure the mesh quality, which represents the relative distortion of the element relative to its ideal shape, 0 is the best and 1 is the worst. The average skewness of the whole mesh is 0.31215, close to 0, indicating that the mesh quality is good and can obtain more accurate finite element analysis results.

The structure of the vibration exciter is relatively complex, which will affect the calculation efficiency of the finite element analysis. Therefore, this study uses the mass point in the Workbench to replace the vibration exciter. Two mass points are respectively arranged at the connection between the vibration exciter and the screen body, shown in Fig. 3(b). The exciting force on the vibrating screen comes from the rotation of the eccentric blocks inside the exciter. According to the vibration parameters of the used exciter, the exciting force can be calculated, and the included angle with the horizontal direction is 45°, which acts on the connection between the exciter and the screen body. In order to simulate the impact of coal particles on the screen body during the operation of vibrating screen, the impact force is applied on the support beams in a vertical downward direction.

Spring constraints are applied to the finite element model of the vibrating screen to simulate the rubber spring. Since the rubber spring has both longitudinal and transverse stiffness, a vertical spring and two horizontal springs are respectively arranged at each spring support. The stiffness of the horizontal spring is 1/3 of that of the vertical spring. One end of the spring is connected to the body, and the other end is connected to the ground, the connection effect is shown in Fig. 3(b).

Fig. 3Finite element model of vibrating screen

a) Mesh division

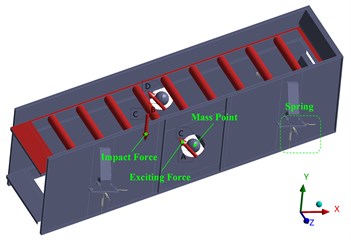
b) Boundary conditions

4. Modal analysis

Modal analysis is mainly to solve the natural characteristics of the system, including natural frequency and natural vibration mode. The natural characteristics of the system are mainly affected by its own structure and boundary constraints, and are independent of the external loads on the system. By comparing the natural frequency with the working frequency, whether the structure has resonance can be known; by observing the natural mode, the weak link of structural deformation can be understood.

Setting the solution parameters and conducting the modal analysis on 2460 double-layer circular vibrating screen, the first nine natural frequencies of the vibrating screen can be obtained, as shown in Table 2. Fig. 4 shows the first nine natural vibration modes of the vibrating screen under natural frequencies excitation. Fig. 4(a) shows the first order vibration mode of the vibrating screen, the screen body makes rigid body translation along the $z$-axis. Fig. 4(b) shows the second order vibration mode of the vibrating screen, the screen body makes rigid body translation along the $x$-axis. Fig. 4(c) shows the third order vibration mode of the vibrating screen, the screen body makes rigid body translation along the $y$-axis. Fig. 4(d) shows the fourth order vibration mode of the vibrating screen, the screen body makes rigid body rotation around the $z$-axis. Fig. 4(e) shows the fifth order vibration mode of the vibrating screen, the screen body makes rigid body rotation around the $z$-axis. Fig. 4(f) shows the sixth order vibration mode of the vibrating screen, the screen body makes rigid body rotation around the $x$-axis. Fig. 4(g) shows the seventh vibration mode of the vibrating screen, the discharge end and the baffle rotate reversely around the $x$-axis. Fig. 4(h) shows the eighth vibration mode of the vibrating screen, the discharge end and the baffle translate along the $z$-axis. Fig. 4(i) shows the ninth vibration mode of the vibrating screen, the left and right side plates rotate reversely around the $z$-axis.

Fig. 4Natural vibration mode of vibrating screen

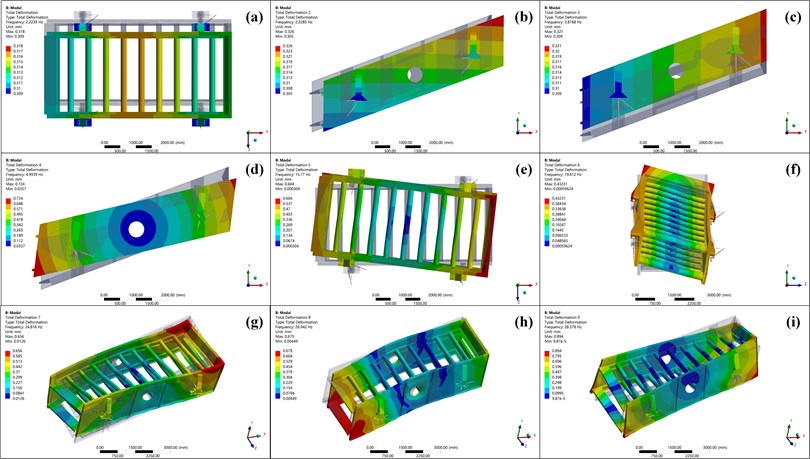
It can be seen from Fig. 4 that the first six vibration modes are rigid body movements of the screen body, only the spring has been deformed, and the screen body has not been deformed. When the exciting frequency reaches the seventh natural frequency, the screen body will occur torsional deformation, and the larger the exciting frequency is, the greater the deformation will occur. Therefore, the working frequency of the vibration exciter cannot exceed the seventh natural frequency (24.818 Hz) of the vibrating screen, otherwise it will cause torsional deformation and damage to the screen body. According to the performance parameters of the motor, the working frequency of the vibrating screen exciter is selected as 16 Hz, and the difference with the seventh natural frequency is 8.818 Hz, 35.531 %, which is a big difference. Hench, when the 2460 double-layer circular vibrating screen works normally, the operating frequency will not cause large screen structure deformation.

5. Harmonic response analysis

The motor generates reciprocating exciting force by driving the eccentric block to rotate, which acts on the whole screen body. The beams and side plates have to bear larger alternating load, resulting in greater dynamic stress. Therefore, it is necessary to conduct dynamic stress analysis on the screen body of the vibrating screen to obtain the stress and deformation distribution of the screen body under the working frequency.

The harmonic response analysis can obtain the steady-state response of the system under the harmonic force, which can be used to analyze the structural response of the vibrating screen under the excitation force. Harmonic response analysis methods include full method, reduced method, and mode superposition method. Since the modal analysis of the vibrating screen has been conducted previously, and modal superposition method is faster and less resources, the mode superposition method is selected as the solution method of harmonic response analysis in this study.

Setting the analysis parameters and selecting the frequency range of 0-20 Hz, the stress and displacement distribution of the vibrating screen at the working frequency of 16 Hz can be obtained, the analysis results are shown in Fig. 5.

Fig. 5Results of harmonic response analysis

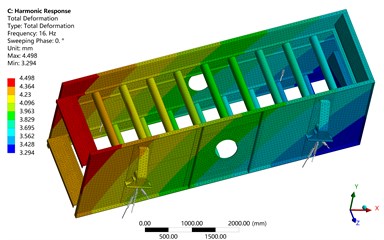
a) Displacement distribution

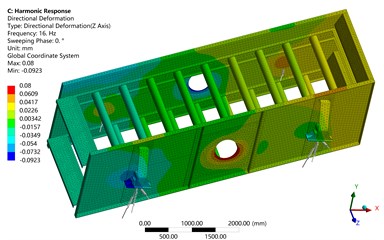
b) Transverse displacement distribution

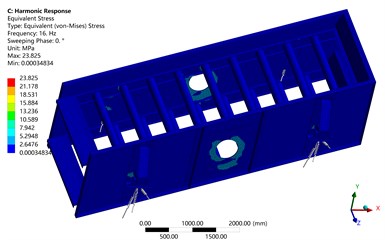
c) Stress distribution

Fig. 5(a) shows the displacement distribution of the vibrating screen. It can be seen from this figure that the overall displacement of the vibrating screen is between 3.5 mm and 4.5 mm. The centroid of the screen body is located at the excitation motor, and the centroid displacement is about 4 mm, which basically meets the design requirements of the vibrating screen.

Fig. 5(b) shows the displacement distribution of the vibrating screen along the $z$-axis, that is, the transverse displacement distribution of the vibrating screen. It can be seen from this figure that the maximum transverse displacement of the screen body is 0.08 mm, close to 0. Therefore, the vibrating screen runs smoothly without transverse swing.

Fig. 5(c) shows the stress distribution of the vibrating screen. It can be seen from this figure that the main stress area of the vibrating screen is mainly concentrated at the connection between the side plates and the exciting motors, where have stress concentration. The maximum dynamic stress of the screen body is 23.825 MPa, which is far less than the yield strength (345 MPa) of the material Q345 used for the vibrating screen, and the safety factor reaches 14.48. The stress values of other parts of the vibrating screen are smaller than 3 MPa. The analysis results show that during the normal operation of the 2460 double-layer circular vibrating screen, the screen body bears a relatively uniform force, has a good bearing capacity, and is not easy to deform and damage.

6. Conclusions

In this study, a novel circular vibrating screen driven by the eccentric shaft, the 2460 double-layer circular vibrating screen, is proposed, which can effectively reduce the concentrated load, and improve the service life and structural reliability of the main shaft. The three-dimensional model of the 2460 double-layer circular vibrating screen is built by Creo, and the finite element model of the vibrating screen is established in ANSYS Workbench. The following conclusions can be obtained:

1) The modal analysis of the vibrating screen is conducted, and the first nine natural frequencies and natural vibration modes of the vibrating screen are obtained. The analysis results show that the operating frequency is far away from the natural frequency, indicating that the vibrating screen will not have resonance during normal operation.

2) The harmonic response analysis of the vibrating screen is carried out, and the displacement and stress distribution of the vibrating screen under the working frequency are obtained. The analysis results show that the vibrating screen operates smoothly without transverse swing, the force distribution of the screen body is uniform, and the stress value is within the allowable stress range of the material, meeting the requirements of the strength and stiffness of the structure.

3) This study provides a design idea for the research and development of the novel vibrating screen. Through three-dimensional modeling and simulation analysis, it can be verified whether the design of the novel vibrating screen is reasonable and meets the industrial demand, and effectively reduces the design cycle and cost.