Abstract
In recent years, many studies have been conducted in bearing fault diagnosis, which has attracted increasing attention due to its nonlinear and non-stationary characteristics. To solve this problem, this paper proposes, a fault diagnosis method based on Empirical Mode Decomposition (EMD), Kernel Principal Component Analysis (KPCA), and Extreme Learning Machines (ELM) neural network, which combines the existing self-adaptive time-frequency signal processing with the advantages of non-linear multivariate dimensionality reduction KPCA approach and ELM neural network. First, EMD is applied to decompose the vibration signals into a finite number of intrinsic mode functions, in which the corresponding energy values are selected as the initial feature vector. Second, KPCA is used to further reduce the dimensionality for a simplified low-dimension feature vector. Finally, ELM is introduced to classify the extracted fault feature vectors for lessening the human intervention and reducing the fault diagnosis time. Experimental results demonstrate that the proposed diagnostic can effectively identify and classify typical bearing faults.
1. Introduction
Rolling element bearings are widely used to support rotating components, whose failures may cause machinery breakdown and economic loss. As a kind of common rotary machinery components, bearings have been conducted much research in Prognostics and Health Management fields. It is crucial to diagnose bearing faults at their early developing stages to prevent severe machinery failures.
Bearing faults are diagnosed mainly by vibration analysis. Vibration signals measured from bearings are complex multi-component signals, generated by tooth meshing, gear shaft rotation, gearbox resonance vibration signatures and a substantial amount of noise. Bearing fault features of vibration signals can be extracted by many methods, such as short-time Fourier transform and wavelet analysis. Wavelet analysis can provide the local features of vibration signals in both the time and frequency domain, so it has been widely used in the roller bearing fault diagnosis. Whereas, energy leakage will occur in wavelet transformation, due to the limitation of the length of the wavelet bases. When scales are determined, the results of wavelet transform would be under the certain scale, whose frequency components may lost a lot of information. And then, Empirical Mode Decomposition (EMD) developed by Huang et al. is demonstrated to be superior to wavelet analysis in many applications [1]. EMD is an adaptive signal processing method developed especially for dealing with nonlinear and non-stationary data. EMD is an approach to the decomposition of nonlinear signal, which can self-adaptive decompose signals into a series of Intrinsic Mode Functions (IMF). The features of vibration signals, in this paper, is extracted by calculating EMD energy entropies of each IMF. But the EMD energy feature vectors always are high-dimensional, which means those are redundancy and difficult to farther calculate. By calculating the eigenvectors of the covariance matrix of the feature vectors, Principal Component Analysis (PCA) can linearly transforms a high-dimensional vector into a low-dimensional vector. Whereas, when dealing with non-linear process, PCA-based feature extraction approaches are limited due to their underlying linearity assumption. Schölkopf [2] et al. described a method for performing a nonlinear form of Kernel Principal Component Analysis (KPCA). KPCA is the reformulation of traditional linear PCA in a high-dimensional space which is related to the input space by a possibly nonlinear map. By using integral operator kernel functions, we could valid employ principal component analysis in a high-dimensional feature space. Recently, the development of neural networks has added new dimensions to diagnose faults of bearings. Neural networks can be used for complex systems which involve non-linear behavior and unstable processes, but there is no standard method to determine their structure and parameters, which determined by researcher using data-driven or experience-based methods. Recently, Extreme Learning Machines (ELM) neural network has been proposed as a simple and efficient approach to build single-hidden-layer feed-forward networks (SLFN) sequentially. ELM use random hidden nodes and find the output weights to minimize the sum-of-squares error in the training set by solving a linear system of equations [3]. ELM learning speed can be much faster than traditional feed-forward network learning algorithms like back-propagation algorithm, with better generalization performance. Compared with BP neural network, ELM provides greater performance at a much faster learning speed and with less human intervention.
In this study, to solve the aforementioned problems, an integrated method that combines EMD-KPCA and ELM is applied to rolling bearing fault diagnosis. Therefore, this paper is organized as follows. Section 2 introduces the details of EMD, KPCA, and ELM; Section 3 describes the validation process of the proposed method; Section 4 concludes this paper.
2. Methodology
First, through the EMD progress the original vibration signals are decomposed to several IMF vectors. After calculating EMD energy entropy, we get energy feature vectors which can illustrate the energy of vibration signal in different frequency bands. Second, a KPCA progress is used to reduce the dimensionality of the energy feature vectors. Third, to identify the fault pattern of the roller bearings, in this paper, an ELM neural network is used to serve as the classifier. And then the feature vectors, calculated by the KPCA process, are taken as the training and testing input.
Fig. 1Process of fault diagnosis
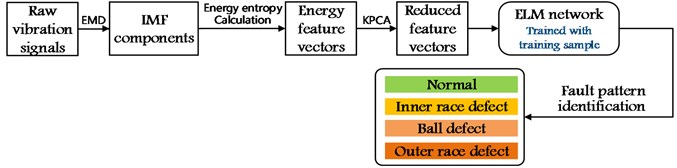
2.1. Empirical mode decomposition
The main function of EMD is to decompose the original vibration signal into a series of IMF, from high frequencies to low frequencies, based on an iterative sifting process. Then the IMF can represent simple oscillatory mode in the signal, with the assumption that signal consists of different simple intrinsic modes of oscillation (i.e., different simple IMF).
With the definition, the vibration signal (thein this paper) is then decomposed into intrinsic modes and a residue [1]:
Thus, the vibration signal can be decomposed into -empirical modes and a residue , which is the mean trend of .
EMD energy entropies of different vibration signals illustrate that the energy of vibration signal in different frequency bands, which will change when bearing fault occurs. To illustrate this change case as mentioned above, the energy of each IMF is calculated.
The energy of the IMF is respectively, is the 2-norm of :
Then the EMD energy feature vector is defined as:
2.2. Kernel principal component analysis
In general, given a set of centered observations , , , . In a dot product space , which is related to the input space by a possibly nonlinear map:
Then we get a set of new data , , . We assume that the new data are centered , and use the covariance matrix in :
Defining an × matrix by:
Now we want to find eigenvalues and eigenvectors satisfying:
And, there exist coefficients such that:
Now we get:
Combining Eqs. (7) and (10), we get:
where denotes the column vector with entries . We can solve an eigenvalue problem to find the solution of Eq. (12):
For the purpose of principal component extraction, we need to compute projections onto the eigenvectors in . Let be a test point, with an image in ; then:
In order to compute dot products of the form , we use kernel representations:
2.3. Extreme learning machine
ELM is an effective learning algorithms of SLFN. ELM has input nodes, hidden nodes, and, output nodes. The hidden biases and input weights and are randomly chosen, and the output weights are analytically determined using Moore–Penrose (MP) generalized inverse.
Given a training set , activation function , and hidden node number :
where is the weight vector connecting theth hidden node and the input nodes, is the weight vector connecting the th hidden node and the output nodes, and is the threshold of the hidden node. denotes the inner product of and.
Step 1: Randomly assign input weight and bias:
Step 2: Calculate the hidden layer output matrix :
Step 3: Calculate the output weight :
3. Experiment results
The data used in the experiment of this paper comes from the bearing data center, which provides access to ball bearing test data for normal and faulty bearings. The bearing data center conducted a series of experiments using a 2 hp Reliance Electric motor, and acceleration data was measured at locations near to and remote from the motor bearings. Three common types of fault of bearing (i.e. inner race defect, ball defect and outer race defect) were seed respectively using electro-discharge machining.
Faults ranging from 0.007 inches in diameter to 0.040 inches in diameter were introduced separately at the inner raceway, rolling element (i.e. ball) and outer raceway. The motor speed is 1750 r/min, and the sampling rate is 120 KHz.
First, the original vibration signals were decomposed into some IMF by EMD. The IMF vectors of every signal had different dimensionality because EMD can self-adaptive decompose signals, as shown in Fig. 2. It is clearly show that only the first several IMF had dominant fault information.
Fig. 2IMF feature vectors
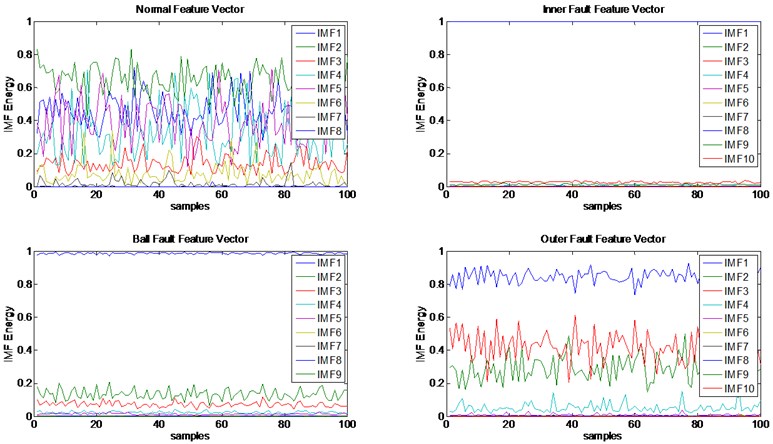
Second, KPCA was used to reduce the dimensionality of the four IMF vectors to eliminate their redundant. The IMF of every samples was converted, separately, to three characteristics, which means each of the new four feature vectors had three rows.
In this paper we use radial basis functions kernel (i.e. ). This kernel is a measure of closeness, equal to 1 when the points coincide and equal to 0 at infinity.
Through this process, not only reduced the data redundancy, also increased the data visibility. As shown in Fig. 3, the four pattern was clearly clustered. The feature vectors calculated by KPCA were separated, for further use, to train-set vectors and test-set vectors.
Finally, an ELM neural network was adopted to identify the various fault patterns. The train feature vector in the four patterns respectively were taken as the ELM neural network inputs, and the hidden layer included 25 nodes. Each pattern was trained by 100 samples, and tested by 20 samples. For the purposes of classification, the four pattern is marked as 1, 2, 3, and 4, respectively.
By applying the ELM neural network that had been trained to the train-set, most of the test samples were identified successfully, as shown in Fig. 4(a). As can be seen from the figure, only the seventh sample was not properly detected, and the accuracy was 98.5 %, which meant the fault diagnosis and fault classification was successfully conducted.
As indicated in Fig. 4, ELM, which only needs to set the node number in the training process, provides higher performance over BP in terms of both learning speed and human intervention. In this case study, the training and testing time was total 0.077838 sec, in which the training and testing samples are 100 and 80, respectively. However, on the same condition, training and testing time of fault diagnosis with BP was 0.870891 sec. The accuracy of bearing fault classification gradually decreases as the node number ranges from 25 to 500 with a step of 25.
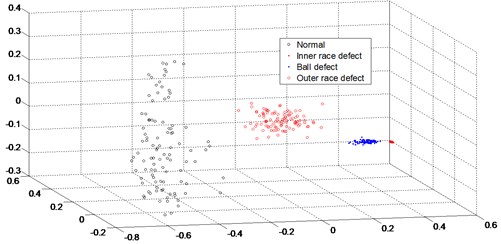
Fig. 3. Pattern clusters
Fig. 4Results of ELM performance verification
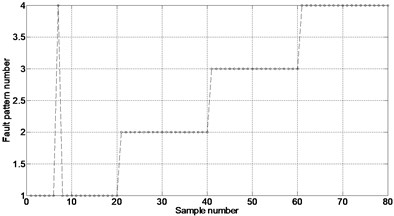
a)
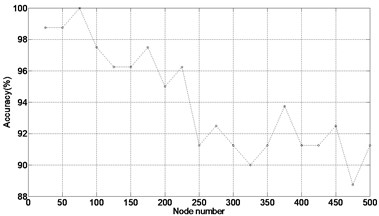
b)
4. Conclusions
This study proposed an efficient algorithm for bearing fault diagnosis based on EMD, KPCA, and ELM. First, feature vectors of vibration signals from bearing are extracted and calculated with EMD, then, to make the diagnosis more accurate and effective, KPCA is introduced to reduce the feature vector dimensions, finally, an ELM network, which is trained with pre-determined samples, are used to classify the fault pattern. The proposed method is demonstrated with several tests, and the accuracy is 98.5 %, meanwhile, the time consuming of ELM is much less, compared with BP neural network.
Future works are expected to focus on two aspects. First, to improve diagnosis accuracy, influence factors of diagnosis, such as the training node number, will be analyzed. Then, comparisons between the proposed methods with traditional diagnosis methods, such as support vector machine, or radial basis neural network, will be conducted.
References
-
Huang N. E., et al. The empirical mode decomposition and the Hubert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, Vol. 454, 1971, p. 903-995, 1998.
-
Schölkopf B., Smola A., Müller K. Nonlinear component analysis as a kernel eigenvalue problem. Neural Computation, Vol. 10, Issue 5, 1998, p. 1299-1319.
-
Romero E., Alquézar R. Comparing error minimized extreme learning machines and support vector sequential feed-forward neural networks. Neural Networks, Vol. 25, 2012, p. 122-129.
About this article
This research was supported by the National Natural Science Foundation of China (Grant No. 61074083, 50705005, and 51105019), and by the Technology Foundation Program of National Defense (Grant No. Z132013B002).
