Bearing fault diagnosis based on TEO and SVM

2.1. Principle of TEO

2.2. SVM

The main idea of SVM is as shown in Fig. 1 [8]. The triangles represent one kind of samples, while circles represent another. H represents the classifying line. H1, H2 are lines parallel to H and they are through the samples which are the closest to H at the same time. The distance between H1 and H2 is defined as class interval. The role of H is to correctly separate two kinds of samples and reaches zero of training error rate. The optimal classifying line is reaching classification margin maximization in Fig. 1.

The equation for classification line is:

Eq. (10) uses normalized treatment and gets linearly separable data sets$\left(x_i,y_i\right)\text{,}$$(i=\text{1,}\text{2,...}\text{,}n)$, $x\in R^d$, $y\in \{$1, –1$\}$ meet the following definitions

2$/‖\omega ‖$ is class interval. The classification margin maximization is the minimum of ${‖\omega ‖}^2$. The optimal classification line is to minimize the ${‖\omega ‖}^2/$2 and meats the type Eq. (11). Support vector is the training samples on H1 and H2.

SVM is developed for a value of two proposed classification problems. However, the bearing fault classification is a multi-class classification problem. So the multi-class classification problem should be converted to two classification problems [9]. This experiment adopts a multi-classifier made of three SVMs.

Fig. 1Optimal classifying line

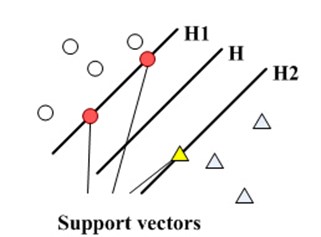
Fig. 2The flow chart of the proposed method

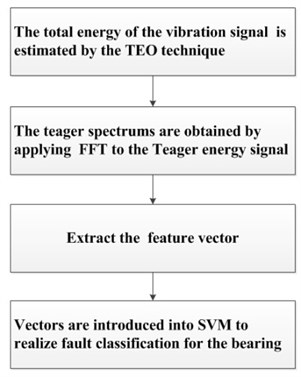
2.3. The procedure of the proposed method

This paper proposes a fault diagnosis method for bearing based on TEO and SVM. First, the total energy of the vibration signal of the bearing is estimated by the TEO technique. Second, the teager spectrums are obtained by applying fast Fourier transform (FFT) to the Teager energy signal [10, 11]. Third, feature vectors are extracted. Finally, these vectors are introduced into SVM to realize fault classification for the bearing.

3.1. Feature extraction

All the rolling bearing data used in this study are acquired by the Bearing Data Center of Case Western Reserve University. In the experiment, natural frequency of bearing used in this paper is $F_{In}=$157.94 Hz, $F_{Out}=$104.56 Hz.

The total energy of the vibration signal of the bearing is estimated by the TEO technique. The time domain – amplitude waveforms are obtained as shown in Fig. 3 by inputting normal data, inner fault data and outer fault data to Teager program, respectively.

In order to obtain Teager spectrum, this paper uses FFT to transform TEO, the results are shown in Fig. 4. Resonance frequency band energy $E_1$ is the energy from 2000 to 4000 Hz. Because energy leakage is inevitable. According to the practice that $\mathrm{\Delta }f=$2 Hz, this experiment chooses $E(F_{IN}\pm 2)$, $E(F_{OUT}\pm 2)$, and $E_1/E_{TOTAL}$ as the feature vectors.

Fig. 3Time domain waveform at outer ring fault condition, inner fault condition, normal condition

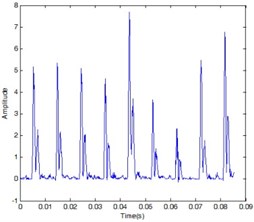
a)

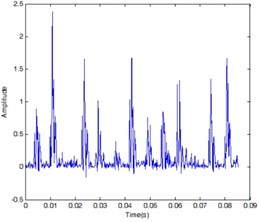
b)

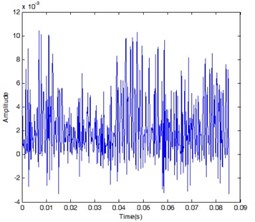
c)

Fig. 4Frequency spectrum at outer ring fault condition, inner fault condition, normal condition

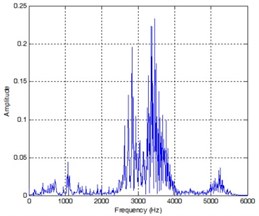
a)

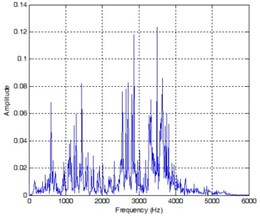
b)

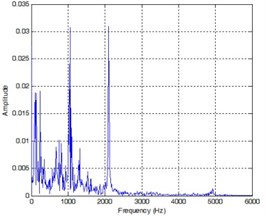
c)

3.2. Fault diagnosis based on SVM

This experiment adopts a multi-classifier composed of three SVMs. The experiment uses a total of 20×3 groups data (each mode is 20 groups) to classify the faults. Set the targets output as Eq. (1), (0, 1) and (0, 0, 1), corresponding to the outer ring fault, the inner ring fault, and the normal condition, respectively. Because the place is limited, only parts of data (3×3 groups) is showed in Table 2.