Piezoelectric actuators and their application in precise-positioning systems and space structures

1. Introduction

Complex vibration drives are frequently used in the optical systems and are mainly applied for space structures purpose. They can add the value for different extremely precise micro and nano motion systems. According to the calculations the vibration drives of constituent elements tied together by binding material (composite piezoconverters) is a system having great static strength. For this reason, these systems are used in mechanisms operating under heavy loads and requiring very precise displacements.

The vibration drives used in mechanisms requiring high precizion displacements have indicated that accuracy depends on design and technological factors. Vibration drives can be bimorph, axial and combined stacks. One of essential requirements for compound vibration drives is their capability of transferring unipolar or bipolar force. In the first version, the vibration drive acting in one direction is made of separate piezoelements and adapted binding materials. They operate under positive deformation (elongation due to neutral position) when the applied voltage is positive with respect to polarization. The vibration drive returns to its initial position under negatyve deformation (contraction) when opposite sign voltage is applied binding materials. Mechanisms of this type are frequently used in adaptive optics and space structures [6].

The second version ensures the possibility of displacements to opposite directions from the neutral position – bipolar force. This happens when the vibrodrive elongates from the initial position due to the positive deformation while the deformation to the opposite direction occurs as a result of the elastic strain. Piezomotors with a compound vibrodrive are superior over those with a single-layer vibrodrives owing to the fact that by summing up the deformation of each element the displacement of acompound piezoconverter can be increased. Their mechanical properties are also significantly augmented.

Therefore, dynamic characteristics of each individual element of compound piezoconvertes have to be determined separately. When assembling the piezoconverter piezoelements with similar characteristics have to be selected. When piezoceramics is deformed by external electric field, the input electrical energy is larger than the output mechanical energy. The ineffective electrical energy is stored as electrostatic energy in the piezoconverter and reverts to the power supply in the final process of an operating cycle.

2. The piezoelectric actuators used in mechanisms requiring high precision displacements

Technical possibilities of combined piezostack used in piezoconverters are analyzed and reported in many works [1-3]. Under severe conditions and environment these structures are to be thoroughly investigated. Mechanical and electrical laws pertaining in combined converters are analyzed and their interrelation is written by the mathematical expression:

where $\sigma$ – mechanical stress; $D$ – vector of electric displacement; [$c^E$] – stiffness tensor; [$e$] – tensor of piezoelectric constant; [${∍}^s$] – tensor of dielectric constant:

where the matrix [$B$] is determined by deformations and displacements $\stackrel{-}{\epsilon }=\left[B\right]{\stackrel{-}{\sigma }}^e$, and the matrix ${\left[B\right]}^T$ is the transformation matrix [$B$] where the matrix [$B$] is determined by deformations and displacements $\stackrel{-}{\epsilon }=\left[B\right]{\stackrel{-}{\sigma }}^e$:

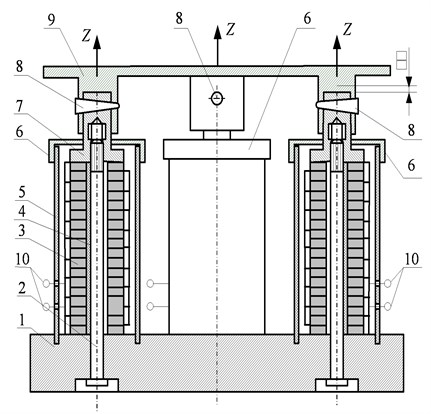
where ${\left[B_L\right]}^T$ is the transformation matrix [$B_L$] estimating nonlinearity of deformations, [$K_{\sigma }$] is the matrix estimates piezoelectric properties described by formulas Eq. (1). The coefficient of proportionality $\lambda$ indicates the extent of the load increase in order to obtain critical strength [$\delta$]. The critical load – $P^{kp}=P^{\lambda }$. Fig. 1 shows a high static strength system composed of the piezoconverters of constituent elements tied together by binding material (piezoelectric actuators) according to the calculations. The values of critical loads are obtained for piezodrives as follows: a) with disk elements $P^{kp}=$ 280244.48 N, b) with ring elements $P^{kp}=$269455.07 N.

Fig. 1Piezoelectric actuators of constituent elements piezostacks containing alternating layers of piezoceramics

a)

b)

For this reason, these systems are used in mechanisms operating under heavy loads and requiring very precise displacements. The piezoactuators used in mechanisms requiring high precision displacements have indicated that their accuracy depends on design and technological factors (Fig. 1). Holographic interferometry method and Polytec Scanning vibrometer PSV-400 used in the experimental work has strengthened the expressions of differential equations and used for describing conclusions of the investigation [4, 5].

Fig. 2Adaptive mirror: 1 – supports, 2 – base, 3 – mirrors, 4 – axial stacks

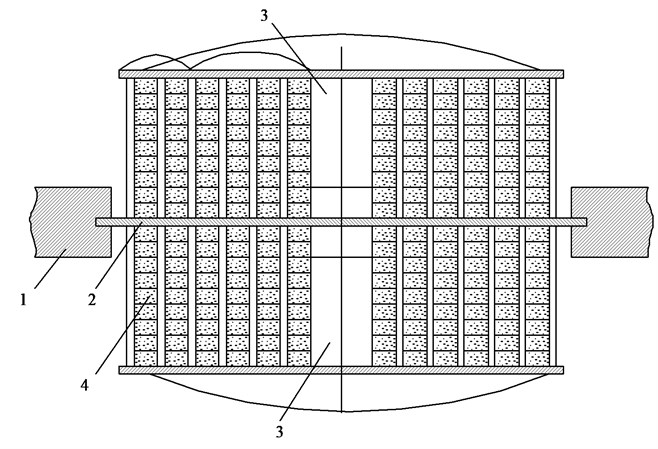
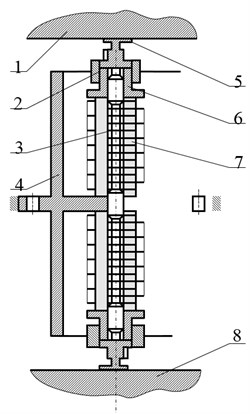
Fig. 3Piezoelectric actuator for optical systems (with three piezostacs)

Fig. 4The application of piezoelectrric actuators in precise-positioning systems and space structures

a)

b)

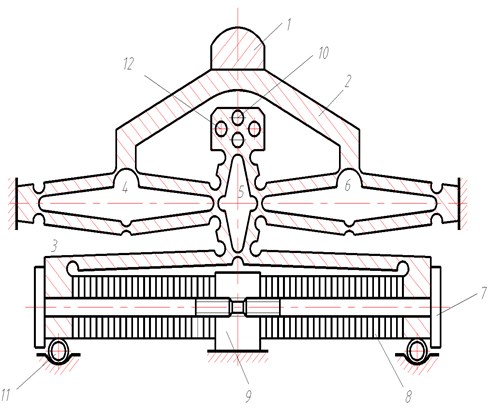
Fig. 5 shows a scheme of operating system and it consists of vibroengine output link 1 immovably fixed in lever system 2 made up of diamond-shaped parts 3 – 6 which are symmetrical with respect to output link 1 displacement. Lever system 2 is rigidly joined to the piezostack by butts and jig 9. The piezostacks are located along one axis perpendicular to that of the displacement motion. Jig 9 is immovably connected to the base to which the lateral supports of lever system 2 are also immovably fixed. The upper support of the lever mechanism is immovably connected to front and back walls immovably set in the base. Two little bearings prevent the lower part of the lever system moving from its equilibrium position. The operation of the vibroengine is as follows: when the supply unit is switched on, the piezostacks subjected to the piezo effect change their size (either elongate or contract). By means of the lever system elastically connected to the working surfaces of piezostacks, the amplified axial displacement of the latter is transmitted to the output link. The displacement power in the lever system is created by diamond-shaped parts.

Fig. 5Piezostacks application in operating system

3. Conclusions

Experimental investigation of compound piezostacks make it possible to determine optimal initial tension force, the dependenceof displacement of a loose piezostack on some constructional and technological parameters. Thereexist the possibilities tooptimize the construction, materials and technology of the piezostack manufacture which can result in the maximum displacement value of a piezostack. All experiments have been carried out under mechanical loads. The analysis has indicated how cautiously should the number of piezoelements for a piezostack be selected for obtaining the higherdisplacement amplitude. By choosing the optimal number of piezoelements, by maintaining the production conditions which do not limit the displacement value but limit the piezostack deflection from the vertical axis it is possible toachieve the desired displacement value with less power and lab our expenditure. The conclusion can be made that stability of piezoengines, the wide range of their control, transmission precision are of never diminishing interest to the scientists investigating piezomaterials. Development of new structures makes it possible to apply them to the design of new technologies.