Optimal maintenance policy for a deteriorating system based on the improved δ-shock maintenance model

Meixia, Tu; Chuan, Lv; Zhou, Dong; Mei-hui, Wang

Vibroengineering Procedia

Browse Procedia

Published: 03 November 2014

Check for updates

Optimal maintenance policy for a deteriorating system based on the improved δ-shock maintenance model

Tu Meixia¹

Lv Chuan²

Dong Zhou³

Wang Mei-hui⁴

^{1, 2, 3, 4}College of Reliability and Systems Engineering, Beihang University, Beijing, P. R. China

^{1, 2, 4}Science and Technology on Reliability and Environmental Engineering Laboratory, Beijing, P. R. China

Corresponding Author:

Wang Mei-hui

Cite the article Download PDF

Downloads 1284

Abstract

In the classic $δ$ model, there is only one threshold for maintenance decision. Taking the different levels of failures causing by shocks into account, the interval between successive shocks and different thresholds should be considered when making replacement decision. This paper proposes a replacement policy based on multi-threshold for a deteriorating system which is subject to $δ$ -shock. This approach assumes the failure thresholds will geometrically decrease with the increasing repair times, and. The optimal replacement policy $N$ is determined by using this method, and the average cost in life cycle is minimized. A numerical case study is conducted to validate the related concept and maintenance decision-making model. The results indicate that the proposed method can effectively optimize the maintenance policy and minimize the life-cycle cost.

1. Introduction

It is generally known that the maintenance decision-making is based on the assumption “A repairable system is as good as new after maintenance” in the earlier research. That is so-called “the perfect repair”. For a deteriorating system, it is not always as true as it is. With the performance degradation of the system, it maybe need much more time to restore it. Barlow and Hunter [1]. first introduced the minimal repair model. In this model, the system continued to run after repair, while the failure rate after repair would be as well as before. Brown and Proschan [2] put forward an imperfect repair model, and a perfect repair with probability $p$ and minimal maintenance with probability $1 - p$ . In addition, Lam and Stanley et al has done much related research [3-4].

$δ$ -shock is one of the shock model, and proposed by Lam Yeh at first. In the $δ$ -shock model, a shock is fatal if the interval between this and last shock arrival time is not greater than a specified threshold $δ$ . The threshold $δ$ is usually a constant. Wang Guan Jun [5] studied the $δ$ -shock model for the optimal replacement policy based on the random variable $δ$ . Wang Xiao Lin et al. [7] assumed that the system has two kinds of failure mode, and established an imperfect repair model by constraint of availability. Recently, Chen guoqing and Lam Ling et al. [7] proposed a multi-threshold method for reducing the system operation cost and optimizing the replacement policy [7].

In summary, the $δ$ -shock model has been applied in many cases of deteriorating law, and so has geometric process in maintenance. However, there are still some problems: 1) Rarely considering the combine the $δ$ -shock model with geometric process to establish the deteriorating system maintenance policy; 2) Seldom considering the maintenance policy by constraint of availability; 3) Although some literatures have already considered different failure state, the probability of different failure state is not clear. To solve the above problems, we propose the improved $δ$ -shock model.

2. Definition and assumption

Definition 1 [8]. Given two random variables $X$ and $Y$ , $P (X > a) \geq P (Y > a)$ if for all real $t$ ;Then $X$ is called stochastically larger than $Y$ or $Y$ is stochastically less than $X$ . This is denoted by $X_{n} \geq (\leq) X_{n + 1}$ .

Definition 2. A stochastic process $\{τ_{n}, n = 1,2, \dots\}$ is called a geometric process (GP), if there exists a real $a > 0$ , such that $\{a^{n - 1} τ_{n}, n = 1,2, \dots\}$ forms a renewal process (RP). Real number $a$ called the ratio of the GP.

The $δ$ -shock maintenance model for a deteriorating system is introduced here by making the following assumptions.

Assumption 1. At the beginning a new system is installed. Whenever the system fails, it will be repaired or replaced. The system will be replaced by an identical new one sometime later. The system requirement is that the system steady availability is not less than $A_{0}$ .

Assumption 2. In $δ$ -shock model, the shocks will arrive according to a renewal process with inter-arrival times having a general distribution $F (t)$ .

Assumption 3. In $δ$ -shock model, if the system has been repaired for $n$ times $(n = 1,2, \dots)$ , the threshold of a failure shock will be $b^{n} δ$ $(b > 1)$ where $b$ is the rate and $δ$ is the threshold of a failure shock for a new system. This means that whenever the time to the first shock following the nth repair or an inter-arrival time of two successive shocks after the $n$ th repair is less than $b^{n} δ$ , the system will fail. During the repair time, any shock arriving when the system is ineffective, under repair

Assumption 4. In the improving $δ$ -shock model, Assume that the system has two failure threshold $δ_{1}$ , $δ_{2}$ , $({δ_{1} > δ}_{2})$ . If shock interarrival time of two successive shocks $t \in (δ_{2}, δ_{1})$ , the failure system is the first type of failure state, and the system need repair; If the failure system is the second type of failure state, we need replace a new system.

Assumption 5. Assume that $p_{i k}$ is condition probability of the $i$ th type $(i = 1,2)$ failure state when system occurs the $k$ th failure. Then under Assumptions 2, the system failure probability is $p (t < b^{k - 1} δ_{1}) = F (b^{k - 1} δ_{1})$ , and:

p_{1 k} = \frac{F (b^{k - 1} δ_{1}) - F (b^{k - 1} δ_{2})}{F (b^{k - 1} δ_{1})}, p_{2 k} = \frac{F (b^{k - 1} δ_{2})}{F (b^{k - 1} δ_{1})} .

Assumption 6. By applying the replacement policy $N$ , the system has been replaced by an identical new one at the time following the $N$ th failure of the 1th failure. The replacement time is a random variable $Z_{1}$ with $E (Z_{1}) = β_{1}$ ; When the system is subject to the 2th kind failure, the failure is deadly, the system must be replaced immediately; The replacement time is a random variable $Z_{2}$ with $E (Z_{2}) = β_{2}$ .

Assumption 7. Let $Y_{i}$ be the repair time of the system after the $i$ th failure. Then the repair time constitutes a GP with ratio $θ$ . Thus $E (Y_{n}) = θ^{n - 1} μ$ .

Assumption 8. The repair cost has a constant rate $c_{r}$ , and the unit reward when the system is operating has a GP with ratio $k$ $(0 < k \leq 1)$ , this is $c_{w}^{n} = c_{w} k^{n}$ . The replacement cost comprises two parts: the basic replacement cost $R,$ and The other ones are cost proportional to the replacement time $Z_{1}$ at a constant rate $c_{1}$ and the replacement time $Z_{2}$ at a constant rate $c_{2}$ .

Remarks

First, Policy $N$ we adopt in Assumption 3 we explain the reason of using replacement policy $N$ . Besides policy $N$ , policy $T$ is also applied, by which the system will be replaced by an identical new one at a stopping time $T$ . However, for the long-run average cost case, policy $N^{*}$ is at least as good as an optimal policy $T^{*}$ . Thereafter Lam proved that the above result is true.

Second, for a deteriorating system, it will be more fragile and easier to break down after repair. As a result, the failure threshold $δ$ of the system will be increasing with the number of repairs taken; the operating reward of the system will be smaller and smaller, while the consecutive repair times of the system will be longer and longer. Assumption 3, 7 and 8 are approximated to the geometric process of the above situations.

Third, due to ageing effect and accumulated wearing, it is reasonable to assume that the reward operating for a deteriorating system form a decreasing GP, and the consecutive repair times for the system constitute an increasing GP. This is not only based on our general knowledge but also on the result in real data analysis, and Lam and Chan have studied related research. It was shown that on average the GP model has been applied to the maintenance problems is reasonable.

3. Determining the length of a renewal cycle

First of all, we define a cycle is completed if a replacement is completed. Therefore, a cycle is actually either a time interval between the installation of a system and the first replacement or a time interval between two consecutive replacements.

Now, assume a replacement policy $N$ is adopted. Let $W$ be the length of a cycle under replacement policy $N$ ; Assume that $P_{1}$ is $N$ times of failure are first one and $P_{2}$ is before the $(m - 1)$ times of failure are first failure, the first is the second in the $m$ time; it follows from Assumption 6 that:

1

E (W) = E (\sum_{n = 1}^{N} X_{n} + \sum_{n = 1}^{N - 1} Y_{n} + Z_{1}) P_{1} + \sum_{m = 1}^{N} E (\sum_{n = 1}^{m} X_{n} + \sum_{n = 1}^{m - 1} Y_{n} + Z_{2}) P_{2} .

It follows from Assumption 4 and Assumption 5 that $P_{1} = \prod_{k = 1}^{N} p_{1 k}$ , $P_{2} = \prod_{k = 1}^{m - 1} p_{1 k} ∙ p_{2 m}$ .

According to the analysis method of the length of a renewal cycle, we can get the operating time in a renewal cycle $U (N)$ , then:

2

E (U (N)) = E (\sum_{n - 1}^{N} X_{n}) \prod_{k = 1}^{N} p_{1 k} + \sum_{m = 1}^{N} E (\sum_{n = 1}^{m} X_{n}) \prod_{k = 1}^{m - 1} p_{1 k} ∙ p_{2 m} .

Further, based on the renewal theorem, we can get the system of steady-state availability $A (N) :$

3

A (N) = \frac{E (U (N))}{E (W)} .

Let the cost be $C (N)$ , It follows from Assumption 7 with the help of Eq. (1) that it is easy to get the cost of a renewal cycle:

4

C (N) = (c_{r} \sum_{n = 1}^{N - 1} Y_{n} - c_{w} \sum_{n = 1}^{N} k^{n} X_{n} + R + c_{1} Z_{1}) \prod_{k = 1}^{N} p_{1 k}

+ \sum_{m = 1}^{N} (c_{r} \sum_{n = 1}^{m - 1} Y_{n} - c_{w} \sum_{n = 1}^{m} k^{m} X_{n} + R + c_{2} Z_{2}) ∙ \prod_{k = 1}^{m - 1} p_{1 k}^{m - 1} ∙ p_{2 m}

5

E (C (N)) = (c_{r} \sum_{n = 1}^{N - 1} E (Y_{n}) - c_{w} \sum_{n = 1}^{N} k^{n} ∙ E (X_{n}) + R + c_{1} E (Z_{1})) ∙ \prod_{k = 1}^{N} p_{1 k}

+ \sum_{m = 1}^{N} (c_{r} \sum_{n}^{m - 1} E (Y_{n}) - c_{w} \sum_{n = 1}^{m} k^{m} ∙ E (X_{n}) + R + c_{1} E (Z_{1})) \prod_{k = 1}^{N} p_{1 k}

+ \sum_{m = 1}^{N} (c_{r} \sum_{n = 1}^{m - 1} E (Y_{n}) - c_{w} \sum_{n = 1}^{m} k^{m} E (X_{n}) + R + c_{2} E (Z_{2})) ∙ \prod_{k = 1}^{m - 1} p_{1 k} ∙ p_{2 m} .

Let the average cost be $c (N)$ , according to the renewal theorem, $c (N)$ is given by:

6

c (N) = \frac{E (C (N))}{E (W)} .

4. Establishing maintenance policy model

Now, by using Eq. (2)-(6), it is easy to get the explicit expression of the long-run average cost per unit time is derived on the constraint of availability:

7

m i n \{\frac{E (C (N))}{E (W)}\}, s . t \{\frac{E (U (N))}{E (W)}\} \geq A_{0} .

To solve the above model, the main problem is to solve out $E (C (N))$ , $E (U (N))$ , $E (W)$ , it from Eq. (4) and (5) know that it is key to get $E (X_{n})$ , $E (Y_{n})$ , $E (Z_{1})$ , $E (Z_{2})$ and $E (Z_{1}) = β_{1}$ , $E (Z_{2}) = β_{2}$ , thus, the problem is reduced to find the values $E (X_{n}) .$

Let $M_{n}$ be the shock time of the system following the $n$ th operating, denote the system is subject to $M_{n} - 1$ time shock without failure, and in the $M_{n}$ shock to fail. It is easy that $M_{n}$ obey to the geometric distribution. Therefore:

8

p (M_{n} = l) = p {(τ > b_{n - 1} δ_{1})}^{l - 1} ∙ p (τ < b_{n - 1} δ_{1}) = {[1 - F (b_{n - 1} δ_{1})]}^{l - 1} F (b_{n - 1} δ_{1}),

l = 1,2, \dots .

Let $V_{n i}$ be the shock inter-arrival time of the $i$ th shocks time of the system following the $n$ th operating $(i = 1,2, \dots, M_{n})$ . Hence:

9

E (V_{n i} | V_{n i} > b^{n - 1} δ_{1}) = \frac{\int_{b^{n - 1} δ_{1}}^{+ \infty} t f (t) d t}{1 - F (b^{n - 1} δ_{1})},

10

E (V_{n M_{n}} | V_{n M_{n}} > b^{n - 1} δ_{1}) = \frac{\int_{0}^{b^{n - 1} δ_{1}} t f (t) d t}{F (b^{n - 1} δ_{1})} .

It from Eq. (9), (10) know that it is easy to get $E (X_{n})$ :

11

E (X_{n}) = \sum_{l = 1}^{\infty} E (X_{n} | M_{n} = l) p (M_{n} = l)

= \sum_{l = 1}^{\infty} [(l - 1) \frac{\int_{b^{n - 1} δ_{1}}^{+ \infty} t f (t) d t}{1 - F (b^{n - 1} δ_{1})} + \frac{\int_{0}^{b^{n - 1} δ_{1}} t f (t) d t}{F (b^{n - 1} δ_{1})}] {[1 - F (b^{n - 1} δ_{1})]}^{l - 1} F (b^{n - 1} δ_{1})

= \frac{\int_{0}^{+ \infty} t f (t) d t}{F (b^{n - 1} δ_{1})} = \frac{\int_{0}^{+ \infty} e x p (- {(t η^{- 1})}^{γ}) ∙ {(\frac{t}{η})}^{γ - 1} ∙ \frac{γ}{η} d t}{1 - e x p (- {(t η^{- 1})}^{γ})} .

From what has been discussed above, we can get $A (N)$ and $c (N)$ .

5. Example

In this section, we through a numerical example for the validity of this model. Assume that the shocks will arrive according to a renewal process with interval having Weibull distribution $F (t) = 1 - e x p (- {(t η^{- 1})}^{γ})$ related parameters settings are shown in Table 1.

Table 1Parameter setting table

$δ_{1}$	$δ_{2}$	$c_{r}$	$c_{w}$	$c_{1}$	$c_{2}$	$R$	$k$	$b$	$θ$	$μ$	$β_{1}$	$β_{2}$	$η$	$γ$
4.5	1.5	30	80	50	80	400	0.85	1.02	0.75	6	2	4	10	2

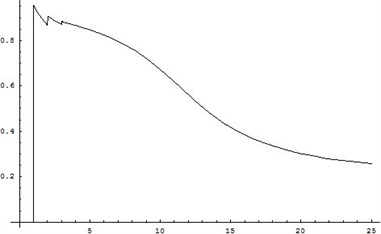
In combination the above parameters with the explicit expression of $A (N)$ and $c (N)$ , by the numerical calculation, we can know the concrete result $A (N)$ sand $c (N)$ , seeing in Table 2, and the trend of $A (N)$ with $N$ is shown in Fig. 1, and the $c (N)$ trend of with N is shown in Fig. 1. From Fig. 1 and Fig. 2 with help Table 2, it is easy that the min cost radio be $c (1) = - 46.93$ with the system of steady-state availability $A (N)$ to the max, this is $A (1) = 0.95$ . In conclusion, the optimal replacement policy $N^{*}$ is get.

Table 2The Result of cN and AN

$N$	$c (N)$	$N$	$c (N)$	$N$	$c (N)$	$N$	$A (N)$	$N$	$A (N)$	$N$	$A (N)$
1	-46.93	6	-24.93	11	-13.44	1	0.95	6	0.82	11	0.59
2	-40.22	7	-22.48	12	-12.11	2	0.91	7	0.79	12	0.53
3	-35.14	8	-20.31	13	-10.91	3	0.88	8	0.75	13	0.48
4	-31.08	9	-18.34	14	-9.84	4	0.86	9	0.71	14	0.43
5	-27.75	10	-14.92	15	-8.89	5	0.84	10	0.65	15	0.39

Fig. 1c(N) against N for Weibull distribution

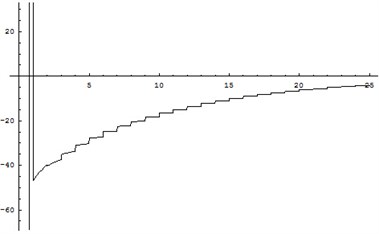
Fig. 2A(N) against N for Weibull distribution

6. Conclusions

In this paper, we proposed a $δ$ -shock model based on multi-threshold. Based on different degrees of failure caused by different interval of two successive shocks, the different failure thresholds were made. The failure level was determined by the failure threshold $δ$ . For a deteriorating system, it would be more fragile and much easier to break down after repair. We characterized the deterioration as following: 1) the failure threshold of the system will increase; 2) the repair time will increase; 3) the reward of system operation will decrease, to make it much more close to the reality. In this paper, the optimal replacement policy N was presented analytically. And it provided a numerical example to illustrate the proposed model, and validated the rationality of the method. It would have theoretical and practical significance for the analysis of the degradation system maintenance policy.

In addition, the model applies to many reliability systems, for example electronic equipment, machinery and computer systems, which makes that the model is successful in a larger scale. In this model, we do not need specific distribution of correlated random variables, thereby, the model needs less constrains. To make the model more perfect and practical significance, further research is that preventive repair is taken into the model. Besides, as the system parameter, the threshold value can be estimated. Few papers studied it. A continuation of this work intends to investigate the parameter.

References

Barlow R. E., Hunter L. C. Optimum preventive maintenance policy. Operations Research, Vol. 8, 1960, p. 99-100.

Search CrossRef
Brown M., Proscham F. Imperfect repair. Application Probability, Vol. 20, 1983, p. 851-859.

Search CrossRef
Lam Y. A geometric process maintenance model. Southeast Asian Bulletin of Mathematics, Vol. 27, 2003, p. 295-305.

Search CrossRef
Lam Y. An optimal repairable replacement model for deteriorating systems. Journal of Applied Probability, Vol. 28, 1991, p. 843-851.

Search CrossRef
Wang Guanjun, Zhang Yuan General δ-shock model and its optimal replacement policy. OR Transactions, Vol. 7, Issue 3, 2003, p. 75-82.

Search CrossRef
Wang Xiaolin, Cheng Zhijun, Guo Bo, et al. Imperfect maintenance decision for a deteriorating system based on shock model. Systems Engineering Theory and Practice, Vol. 31, Issue 12, 2011, p. 2380-2386.

Search CrossRef
Cheng Guoqing, Li Ling, Liu Bingxiang, et al. Optimal maintenance strategy for an extended δ-shock model with multi-failure thresholds. Mathematics applicata, Vol. 26, Issue 1, 2013, p. 165-171.

Search CrossRef
Ross S. M. Stochastic Processes. New York, Wiley, 1996.

Search CrossRef

About this article

Received

Accepted

15 September 2014

Published

03 November 2014

Keywords

improved δ-shock model

failure threshold δ

geometric process

replacement policy N

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.